微起爆序列界面间隙对其传爆性能影响的仿真研究

罗德宏，李 慧，张晶鑫，任 炜，白颖伟，王可暄，尹 明

（1. 海军驻西安弹药专业军事代表室，陕西 西安，710061；2. 陕西应用物理化学研究所 应用物理化学国家级重点实验室，陕西 西安，710061）

微起爆序列界面间隙对其传爆性能影响的仿真研究

罗德宏1，李 慧2，张晶鑫2，任 炜2，白颖伟2，王可暄2，尹 明2

（1. 海军驻西安弹药专业军事代表室，陕西 西安，710061；2. 陕西应用物理化学研究所 应用物理化学国家级重点实验室，陕西 西安，710061）

为研究微起爆序列中结构间隙对传爆性能的影响，基于有限元分析方法，建立了微起爆序列仿真模型，并运用JWL和Lee-Tarver方程进行计算，得到了起爆二级药柱的3种尺寸微药柱的临界间隙值。将仿真结果进行试验验证，结果表明仿真结果能够准确地反映实际情况。

起爆序列；微小型；仿真分析；传爆

MEMS火工品作为第四代火工品，在战略导弹、核武器及航空航天领域均有较为广泛的应用潜力，其中微小型化传爆序列是实现MEMS火工品在引信系统应用的重要技术，美国将其列为实现引信安全和发火系统体积减小、降低成本的4项关键技术之一[1]。微起爆序列是一系列火工品的组合，其作用是将一个很小的初始能量通过爆炸元件逐级放大，输出爆轰能量，以引爆弹药或者爆炸装置中的主装药。但微起爆序列与传统起爆序列在传爆机理方面存在本质区别，目前研究结果较少，并且微起爆序列装药药剂类型、装药量及装药方式不同，因此需针对其传爆可靠性及安全性进行研究。本文采用数值仿真与试验验证相结合的方法，研究微起爆序列间隙对MEMS火工品微序列起爆能力的影响和临界起爆判据，为提高MEMS火工品微起爆序列安全性可靠性设计提供依据。

1 微起爆序列间隙起爆数值模拟

1.1 微起爆序列间隙起爆模拟方法

本文研究内容为直列式微起爆序列，作用过程为微雷管起爆一级药柱，通过结构间隙对二级药柱作用。微起爆序列中一级药柱为密度1.84g/cm3，直径分别为φ1mm、φ1.5mm、φ2.0mm，径高比为1的CL-20，二级药柱为密度1.84g/cm3的JO-9C，尺寸φ 4mm× 4mm。试验装置的约束材料选用不锈钢，结构如图1所示。

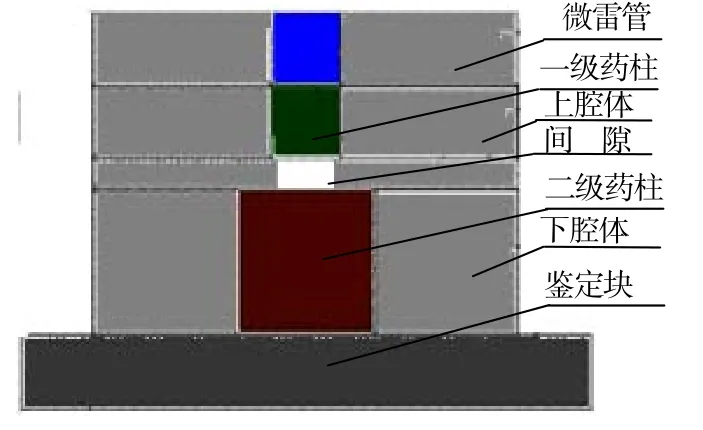
图1 试验结构装置Fig.1 Testing device

运用AUTODYN有限元软件对微火工序列间隙起爆进行仿真研究[2]，涉及的材料包括药柱材料、空气介质、壳体及鉴定块材料。一级药柱、二级药柱的爆轰为非线性流体力学问题，壳体及鉴定块材料涉及固体大变形[3]，所以，研究涉及到流体、固体相互作用时，选用流固耦合法进行仿真计算。

为准确地对问题进行模拟，需对结构进行合理假定：微起爆序列中所有材料初始应力为零，除炸药受到壳体约束，其余边界为自由面；药柱为均匀密度。模拟过程从一级药柱开始，以中心点起爆方式起爆。

1.2.1 有限元模型

微起爆序列为轴对称结构，根据其旋转对称性，取一级药柱底面中心点为坐标原点，X轴为对称轴建立模型，如图2所示，考虑微起爆序列仿真精确度及计算时间，有限单元大小设置为0.1mm。

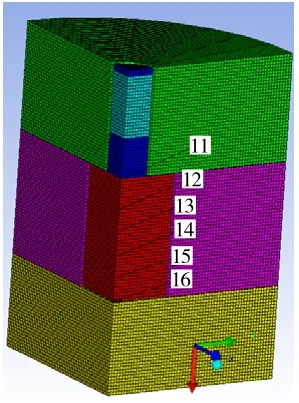
图2 简化后仿真有限元模型Fig.2 Simplified model of device

在模型轴对称中心建立观测点，获取压力时间曲线，二级药柱是否被起爆由观测点压力曲线判断。

1.2.2状态方程

微起爆序列仿真材料包括约束壳体、鉴定块、空气、药柱。高速冲击下约束壳体和鉴定块的力学行为选择Gruneisen状态方程计算；空气材料模型采用理想气体状态方程。一级药柱CL-20爆轰及其产物膨胀过程以JWL方程描述[4-6]：

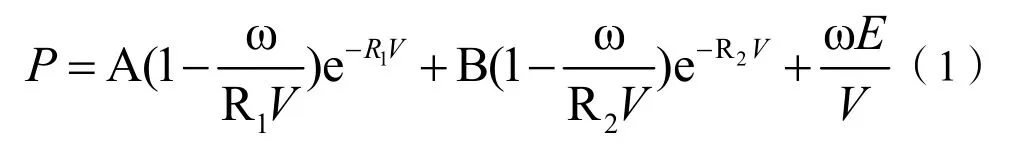
式（1）中：P为爆轰产物的压力；V为相对体积；E为比热力学能；A、B、R1、R2和ω为常数，可通过圆筒试验拟合。其JWL方程参数根据参考文献[7-8]进行设置。

二级药柱由一级药柱爆轰压力引起作用，反应过程不可忽略，以Lee-Tarver方程[9]描述其作用过程。Lee-Tarver方程反应率函数形式为：

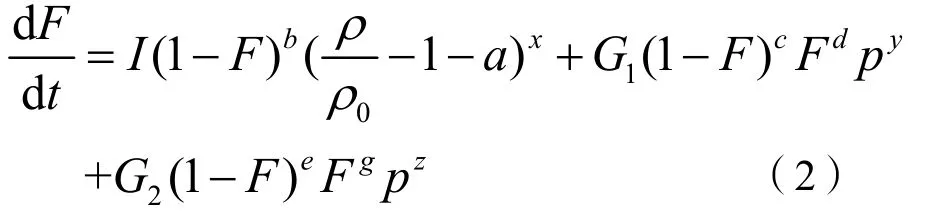
式（2）中：F为炸药反应度，且0≤F≤1，当F=0时，表示炸药未反应，当F=1时表示炸药完全反应；t为时间；ρ为密度；ρ0为初始密度；p为压力；方程中包括12个未知参数：I、b、a、x、G1、c、d、y、G2、e、g和z，见表1。

管理系统评价因子就是对当前管理系统的运行状况进行评价，通常对相关人员采取调查和填表的方式，每部分调查内容都有对应的评价分数，在完成所有对应的评价后，会得到管理系统的评估总分，最后将实际的评估总分转化成FMS，计算如式(4)所示:

表1 仿真中JO-9C的 Lee-Tarver方程参数Tab.1 The simulation parameters of JO-9C of Lee-Tarver equation

2 微起爆序列间隙起爆数值模拟结果

采用流固耦合法对微起爆序列进行仿真，研究密度为1.84g/cm3、不同尺寸的一级药柱起爆二级药柱的临界间隙大小。药柱不同观测点的压力——时间曲线代表药柱不同深度处的爆轰压力值。

2.1 φ2mm×2mm一级药柱的仿真结果

φ2mm×2mm的一级药柱在不同间隙下起爆二级药柱的仿真结果如图3所示。

图3（a）间隙大小为1.5mm，当t=0.4µs时，爆轰到二级药柱底部，观测点压力逐渐上升至28GPa左右，且沿着传播方向稳定传播，二级药柱达到稳定爆轰；图3（b）间隙为2.0mm，当t=0.5µs时，爆轰传到二级药柱底部，沿着爆轰波传播的方向，观测点压力逐渐上升至25GPa左右，与图3（a）情况相同，二级药柱达到稳定爆轰；图3（c）间隙为2.1mm，当t=0.6µs时，爆轰传到二级药柱底部，沿着爆轰波传播方向，药柱底部观测点压力逐渐上升至14GPa左右，然后其压力值随时间下降。随着药柱深度的增加，观测点压力峰值大幅减小，且低于爆轰压力，二级药柱未发生爆轰。

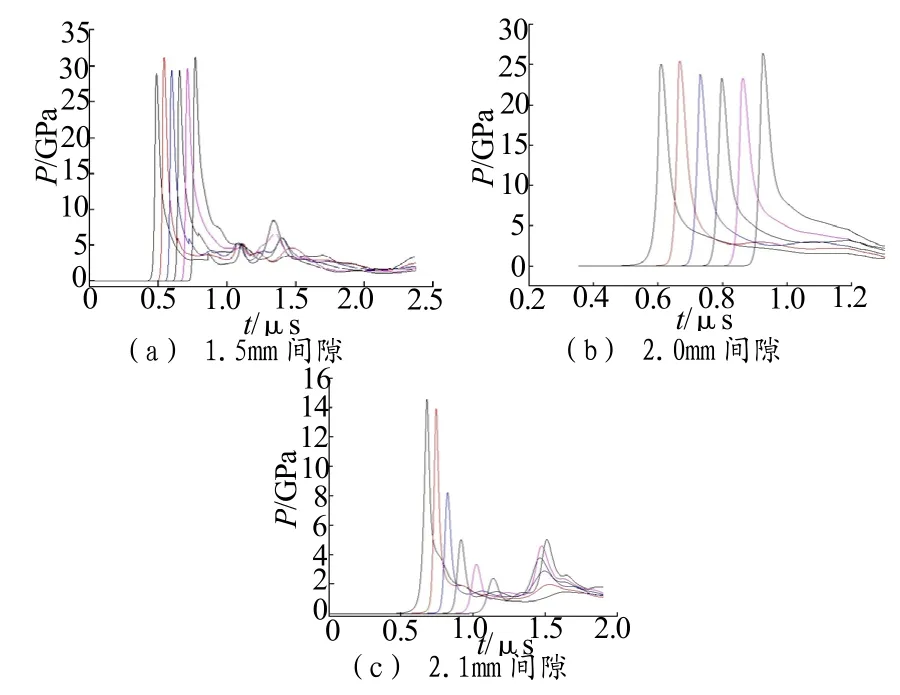
图3 φ2mm×2mm一级药柱、不同间隙下二级药柱上各观测点的压力——时间曲线Fig.3 The P——t curve of gauge points of second grain under φ2mm×2mm first grain and different gap condition

2.2 φ1.5mm×1.5mm一级药柱的仿真结果

φ1.5mm×1.5mm的一级药柱在不同间隙下起爆二级药柱的仿真结果如图4所示。

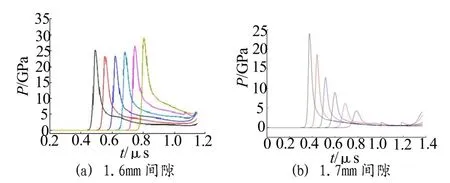
图4 φ1.5mm×1.5mm一级药柱、不同间隙下二级药柱上各观测点压力——时间曲线Fig.4 The P——t curve of gauge points of second grain underφ 1.5mm×1.5mm first grain and different gap condition

由图4（a）可见，间隙1.6mm时爆轰波在药柱内稳定传播，二级药柱爆轰；间隙1.7mm时二级药柱未发生爆轰。当t=0.4µs时，爆轰波传到二级药柱底部，沿着爆轰波传播方向，压力值随时间减小，并且随着药柱深度的增加观测点压力峰值大幅减小，逐渐降至5GPa左右，低于爆轰压力。

2.3 φ1.0mm×1.0mm一级药柱的仿真结果

φ1.0mm×1.0mm一级药柱在不同间隙下起爆二级药柱的仿真结果如图5所示。

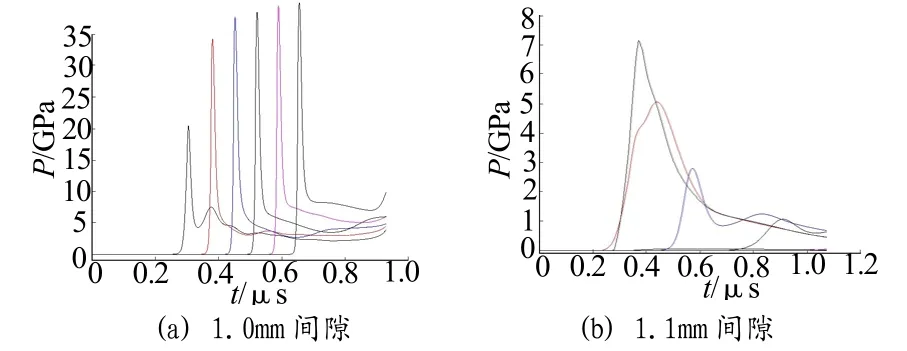
图5 φ1.0mm×1.0mm一级药柱、不同间隙下二级药柱上各观测点压力——时间曲线Fig.5 The P——t curve of gauge points of second grain under φ1.0mm×1.0mm first grain and different gap condition

由图5可见，间隙1.0mm时爆轰波在药柱内稳定传播，二级药柱爆轰；间隙1.1mm时，传到二级药柱底部的压力值低于爆轰压力，二级药柱未发生爆轰。

3 微起爆序列间隙起爆试验验证

3.1 试验装置

通过微起爆序列间隙起爆发火试验对仿真结果进行验证，选用的一级药柱尺寸为φ2mm×2mm，密度为1.84g/cm3，二级药柱尺寸为φ4mm×4mm，密度为1.84g/cm3。采用小雷管对一级药柱起爆，起爆方式为电起爆，发火条件为12V。试验装置中上腔体尺寸为φ1.2mm×0.2mm，下腔体尺寸φ1.2mm×0.4 mm，鉴定块尺寸为φ1.6mm×0.2mm。间隙尺寸如表2所示，试验样品如图6所示。

表2 试验中间隙结构参数Tab.2 The gap size

图6 微起爆序列间隙起爆试验样品图Fig.6 Photo of tested sample

3.2 试验结果

共进行了10发试验，试验结果如表3和图7所示。由表3和图7可见，间隙大小为1.5mm时，二级药柱腔体被炸开，鉴定块凹坑明显，可以断定二级药柱起爆；间隙大小2.0mm时，二级药柱腔体炸裂，鉴定块凹坑也比较明显，二级药柱起爆；间隙大小为2.1mm时，二级药柱腔体完好，鉴定块无痕迹，二级药柱未起爆。将试验结果与仿真结果进行对比，对于φ2mm×2mm的一级药柱，其稳定起爆二级药柱的临界间隙结果是一致的，均为2.0mm。

表3 微起爆序列间隙起爆试验结果Tab.3 The test result of micro train explosive

图7 试验结果Fig.7 Photo of test result

4 结论

本文采用AYTODYN软件对微序列中结构间隙对起爆规律的影响进行仿真计算，并对仿真结果进行试验验证。可以得出如下结论：

（1）通过不同大小CL-20药柱对JO-9C药柱的起爆能力的仿真研究，得到了密度为1.84g/cm3的CL-20起爆JO-9C的临界间隙：一级药柱尺寸分别为φ2mm×2mm、φ1.5mm×1.5mm、φ1.0mm×1.0mm时，其对应的临界起爆间隙分别为2.0mm、1.6mm、 1.0mm。（2）通过对φ2mm×2mm的一级药柱进行间隙起爆试验，证明仿真结果与试验结果是一致的，说明此仿真方法的正确性，可为MEMS火工品微起爆序列设计提供数据支持。

[1]王少卫,聂伟荣.一种微小型传爆序列的设计[J].弹箭与制导学报, 2011, 31(1):107-109.

[2]ANSYS theoretical manua[M]. Livermore Software Technology Corporation,1998.

[3]奥尔连科. 爆炸物理学[M].孙承纬,译.北京:科学出版社,2011.

[4]王辉,沈飞,袁建飞,任新联,张磊.JO-9159炸药强爆轰雨贡纽实验及产物的状态方程研究[J].火炸药学报,2014,37(6): 12-15.

[5]南宇翔,蒋建伟,王树有,陈东萍,等.一种CL-20基压装混合炸药JWL状态方程参数研究[J].含能材料,2015,23(6): 516-521.

[6]穆慧娜,温玉全.基于 NESSUS 的空气隙传爆界面可靠性分析[J].北京理工大学学报,2013,33(4): 331-334.

[7]沈飞,王辉,袁建飞.一种确定JWL状态方程参数的简易算法[J].振动与冲击, 2014,33(9):107-110.

[8]孙占峰,李庆忠,张崇玉.钝感高能炸药爆轰产物JWL状态方程再研究[J].高压物理学报,2010,24(1):55-60.

[9]E. L. Lee, C. M. Tarver. Phenomenological model of shock initiation in heterogeneous explosives[J]. Phys, Fluids,1980,23 (12): 2 362-2 372.

The Simulation on the Effect of Interface Clearance of Micro Explosive Train on Detonation

LUO De-hong1，LI Hui2，ZHANG Jing-xin2，REN Wei2，BAI Ying-wei2，WANG Ke-xuan2，YIN Ming2
(1.Military Representative Office of Naval Ammunition in Xi’an, Xi’an，710061；2. National Key Laboratory of Applied Physics and Chemistry, Shaanxi Applied Physics and Chemistry Research Institute, Xi’an, 710061)

In order to study the effect of structure clearance on detonation capability of micro explosive train, the twodimensional simulation model of micro explosive train is built using the finite element analysis method, and the calculation was carried out using the JWL and Lee-Tarver equation. The critical clearance value for first grain with three diameters were obtained. Then, the simulation result is tested and verified, which shows that the simulation can accurately reflect the actual situation.

Explosive train；Miniature；Simulation analysis；Transmission of detonation

TJ450.2

A

1003-1480（2016）06-0017-04

2016-09-05

罗德宏（1966 -），男，高级工程师，主要从事弹药工程研究。

兵器集团战略基金。