同步轨道双星定位中等频差曲线特性分析

石 荣,姜道安

(电子信息控制重点实验室,四川 成都 610036)

同步轨道双星定位中等频差曲线特性分析

石 荣,姜道安

(电子信息控制重点实验室,四川 成都 610036)

针对同步轨道双星对地面卫星通信类辐射源时差频差定位应用中，用传统方法无法解释等频差曲线的几何物理意义而只能通过复杂数值仿真计算得到的缺点，利用同步轨道双星对地定位中主副星间经度间隔的工程应用约束条件，将地面卫通辐射源与两颗卫星间连线的方向性单位矢量，采用角平分线上的单位矢量进行近似，巧妙地将该问题转为同步轨道单星运动对地所形成的等多普勒曲线问题，从而清晰地展示了模型的几何物理意义，并可快速获得等频差曲线的形状分布与综合定位性能等特性。讨论了等时差与等频差曲线对定位性能的影响，发现在主星选择固定时，在多个满足频率转发条件的副星中选择与主星间相对运动速度较大，且相对运动速度方向尽量平行于地球自转轴线者，能使等时差线与等频差线尽可能形成正交，从而进一步改善定位精度。仿真结果验证了该法的有效性。研究为同步轨道双星定位特性分析提供了新的途径。

同步轨道； 双星定位； 时差频差定位； 无源定位； 等多普勒曲线； 等频差曲线； 等时差曲线； 定位性能

0 引言

利用同步轨道的两颗配置有透明转发器的通信卫星分别接收并转发地面上处于静止状态的卫星通信类辐射源所发射的信号，并测量这两颗卫星接收到信号的时间差(TDOA)和频率差(FDOA)参数，建立起时差方程、频差方程和地球表面位置约束方程，便可求解出该辐射源的位置坐标。这一同步轨道双星TDOA/FDOA定位方法对卫星通信终端和卫星干扰源的定位十分有效，目前已经在各类卫星通信信号及卫星干扰源信号监测系统中得到了应用，并开发了相应的商业化产品[1-2]。十多年来有文献对此同步轨道双星TDOA/FDOA定位方法的技术原理、参数测量与误差分析、定位精度、邻星选择、工程实现、发展趋势和扩展应用等进行了研究，但未对该定位体制中频差方程形成的等频差曲线的相关特性进行深入探讨[3-9]。虽有部分文献对低轨双星定位中的等时差曲线与等频差曲线的特性开展了分析，但同步轨道双星定位与低轨双星定位有较大差异[10]。在低轨双星定位应用中两颗卫星通常是同轨道飞行，相互间隔一定距离，在此条件下两星的速度矢量近似相同；同步轨道双星定位应用中两颗卫星的轨道参数与微动漂移特性各不相同，定位过程中存在两个各异的速度矢量，等频差曲线的形成与这两个各异的运动速度的大小与方向都有关系，难以建立几何意义明晰的简洁数学模型，只能通过复杂的数值仿真计算以获得最终结果。这导致双星定位中邻星选择的多方案对比、定位特性的分析等过程繁琐而复杂，而隐藏于数值计算结果背后的物理规律和几何意义并未得到清晰的解释，从而影响了实际工程应用中定位条件的快速有效构建。

针对这一情况，本文在同步轨道双星对地定位原理简要概述的基础上，阐述了单颗同步轨道卫星运动对信号接收所产生的多普勒效应，讨论了单颗卫星的运动方向对地面上所形成的等多普勒曲线形状的影响。利用同步轨道双星对地定位中主副星经度间隔的工程应用约束条件，将地面卫星通信类辐射源与两颗同步轨道卫星间连线的方向性单位矢量，采用位于这两个矢量构成夹角的角平分线上的单位矢量进行近似，从而将同步轨道双星定位中的等频差曲线问题巧妙地转化成为同步轨道单星对地的等多普勒曲线问题。由此利用已有的分析结果，得到同步轨道双星定位中的等频差曲线的相关特性，给出具直观几何意义的物理解释，以使工程实际应用中对副星的选择和定位特性的分析能快速有效实施。

1 同步轨道双星定位模型

同步轨道双星对地面卫通类辐射源的定位应用场景如图1所示。卫通类辐射源的天线主瓣指向主星，而旁瓣指向副星，所发射的上行信号被卫星上的透明转发器转发后由地面观测站进行接收[2]。

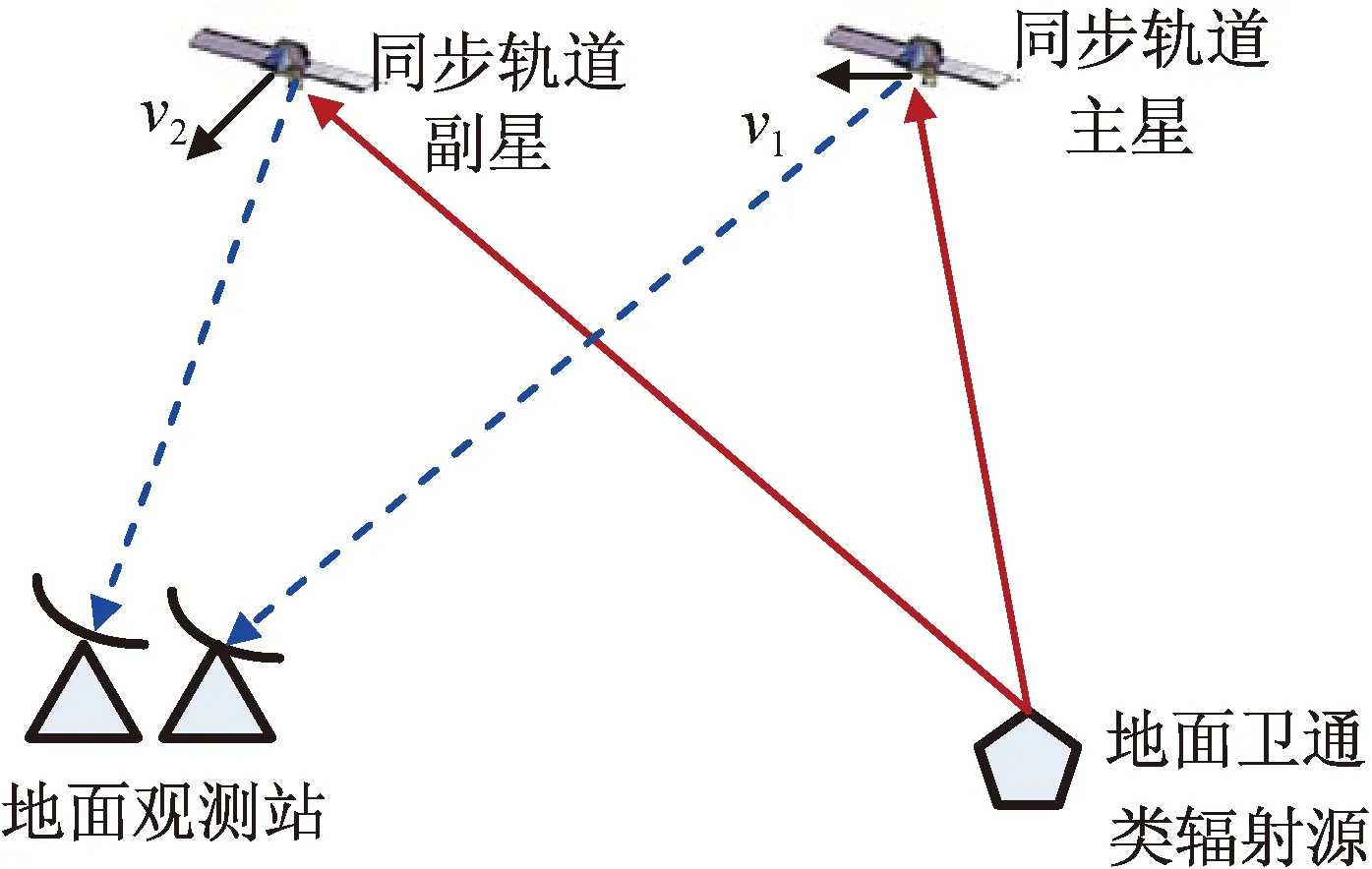
图1 同步轨道双星对地面卫通类辐射源定位场景Fig.1 Geosynchronous orbit dual satellites location for communication equipment on earth

在这一应用场景中，地面卫通类辐射源处于静止状态，地面观测站的位置、2颗同步轨道卫星的位置与速度均为已知量。因在模型建立过程中可补偿掉2颗卫星下行转发至地面观测站路径上的时差与频差，故为简化讨论，在补偿后可只针对2颗卫星接收到的上行信号构建定位模型。

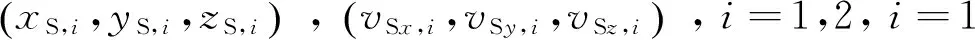
ΔT；

(1)

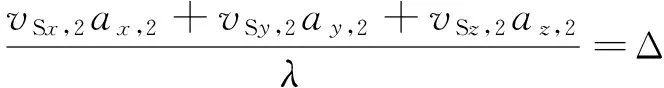
(2)

式中：c为电磁波传播速度；λ为信号波长；[ax,iay,iaz,i]为地面卫星通信终端至第i颗同步轨道卫星的方向性单位矢量(i=1,2)，且

(3)

假设地面卫星通信终端位于地球表面，且地球模型采用球形简化模型，则有

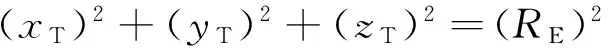
(4)

式中：RE为地球平均半径。

2 单颗同步轨道卫星运动产生的多普勒效应

由于地球偏心率、等轴谐波引起的共振、太阳与月亮引力场、太阳光压等因素的影响，同步静止轨道卫星(后文简称同步轨道卫星)相对地面并不是绝对静止，即卫星轨道的倾角is和偏心率es都不为零，这使同步轨道卫星相对地面作周期性的微小运动。如卫星轨道的长半轴与标准同步轨道半径有差异，卫星还会向东或西发生漂移运动。正是由于上述相对地面的微小运动才导致同步轨道卫星在接收信号时产生了多普勒效应，从而为双星频差FDOA的形成提供了条件。在轨道半径与同步轨道标准半径值相差1km，is=0.000 1°，es=0.000 1条件下，仿真所得同步轨道卫星围绕同步轨道静止参考点处的漂移，以及对应的三维运动速度如图2所示(仿真时间段为24×5h)。

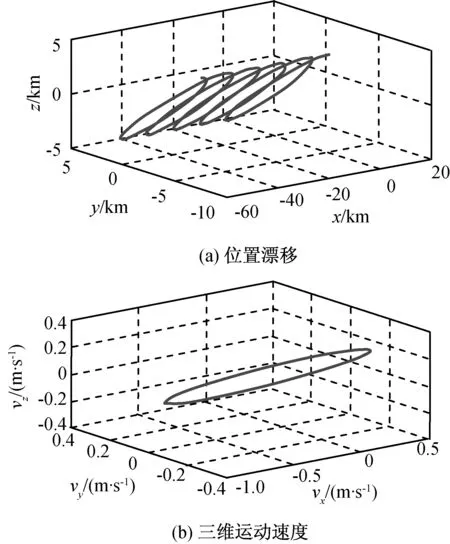
图2 同步轨道卫星微小运动仿真结果Fig.2 Simulation for geosynchronous orbit satellitesmall movement

由图2可知：同步轨道卫星相对地面的运动速度较小，一般为数个米/秒的量级，且以24h为周期变化。由该运动速度可计算出卫星在接收地面卫通类辐射源信号时产生的多普勒频移

fd=vScosθγ/λ.

(5)

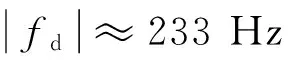
由式(5)可知：在三维空间中由于卫星运动产生的等多普勒频率面是一组圆锥面，其顶点为卫星所在位置处，轴线为卫星运动速度所在方向线。该圆锥面与地球表面相交即形成分布于地球表面的等多普勒曲线簇。对卫星运动速度矢量方向线、地球球心与同步轨道卫星间的连线，设上述两线间的夹角为θγ,e，两线所在平面与地球赤道平面间的夹角为θκ,e。在θκ,e=0，θγ,e取不同典型值情况下，在地球表面产生的等多普勒曲线的形状如图3所示(图中卫星星下点对应经度0°纬度0°的坐标点)。无论卫星的运动速度大小如何改变，图中的等多普勒曲线的形状不会改变，改变的仅是具体的多普勒频率数值。

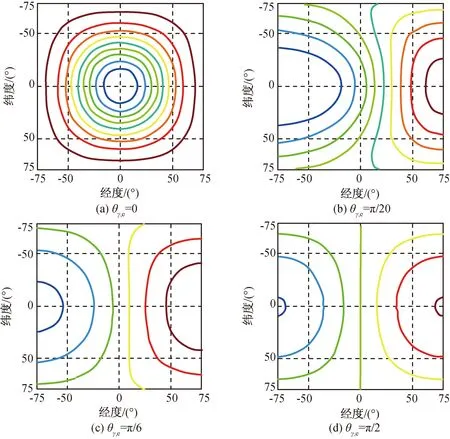
图3 在θγ,e为典型取值时地球表面等多普勒曲线Fig.3 Equal Doppler curves on earth on condition of typical θγ,e

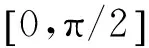
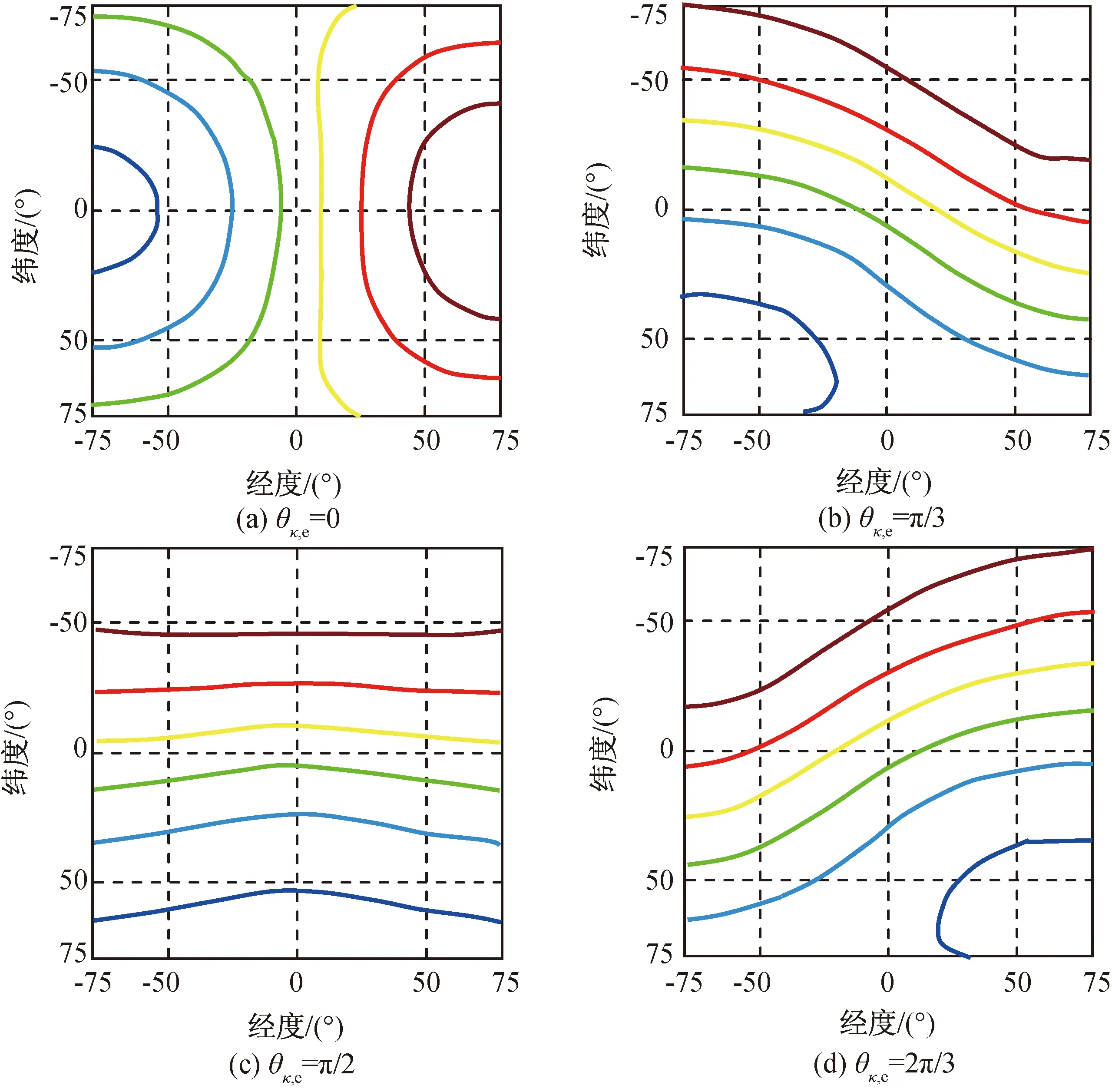
图4 在θκ,e不同取值下地球表面等多普勒曲线旋转效应Fig.4 Rotation of equal Doppler curves on earth on condition of typical θκ,e

图3为θκ,e=0条件下的等多普勒曲线，当θκ,e≠0时，上述等多普勒曲线簇会围绕图3中的中心发生旋转。以图3(c)为例，θκ,e分别为0，π/3，π/2，π2/3时的曲线如图4所示。由图4可明显观察到多普勒曲线的旋转变化。

3 同步轨道双星对地定位的等频差曲线近似逼近

由式(2)可知：在同步轨道双星对地定位模型的频差方程中，绝对频率之差实际上对应了多普勒频率之差，即式(2)中等号左边的被减数与减数分别为两颗卫星对地面卫通类辐射源信号接收时的多普勒频移。虽然从纯粹的数学表达式上看，可由式(2)直接形成等频差曲面，该曲面然后与式(4)表示的地球表面相交，从而形成位于地球表面的等频差曲线，但这样的直接处理，缺乏直观而明晰的几何意义，只能通过数值仿真实现。为解决该问题，可对同步轨道双星定位的等频差曲线进行近似逼近。

根据同步轨道双星定位的实际工程应用条件，为避免地面卫通类辐射源的天线副瓣增益大幅度衰减给时差频差测量带来的低灵敏度问题，一般要求选择的同步轨道主星与副星轨位间的经度间隔不能太大，如在Ku频段通常不超过8°。根据此约束条件，地面卫通类辐射源与两颗同步轨道卫星间的连线的方向性单位矢量[ax,iay,iaz,i]，i=1,2，可用位于这两个矢量构成夹角的角平分线上的单位矢量[bx,Tby,Tbz,T]近似。此处：

(6)

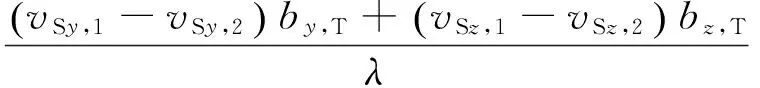
(7)

设两颗同步轨道卫星间的相对运动速度矢量为[vx,Tvy,Tvz,T]，即vx,T=vSx,1-vSx,2，vy,T=vSy,1-vSy,2，vz,T=vSz,1-vSz,2，则式(7)可用两个矢量内积形式表示为

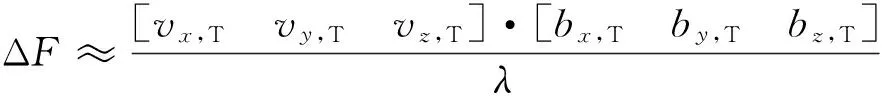
(8)

比较式(5)、(8)可知：式(8)可解释为前文中单星多普勒频移的表现形式，即在同步轨道双星对地面卫通类辐射源的定位应用中所形成的位于地球表面的等频差曲线，可近似认为是两颗卫星间的相对运动速度(具体体现为两者的速度矢量之差)在地球表面产生的等多普勒曲线。

则前文中描述的单颗同步轨道卫星微小运动产生的多普勒效应的相关分析结果可完全对应到同步轨道双星对地频差定位的分析中，即前文所绘制的各种条件下的单星等多普勒曲线对应了同步轨道双星对地等频差曲线。这样，同步轨道双星定位中等频差曲线的直观几何意义就明显展现出了。

4 等时差曲线与等频差曲线对定位性能的影响

同步轨道双星对地面卫通类辐射源的定位主要是基于TDOA，FDOA的测量。对式(1)表达的时差方程来说，其几何意义是以同步轨道的2颗卫星为焦点的旋转双曲面，该双曲面与式(4)表达的地球表面相交，从而形成位于地球表面的等时差曲线。在双星对地面卫通类辐射源的定位应用中，典型的等时差曲线如图5所示。(图5中2颗卫星连线中点的星下点对应经度0°、纬度为0°的坐标点，且2颗卫星间的经度差为6°)。

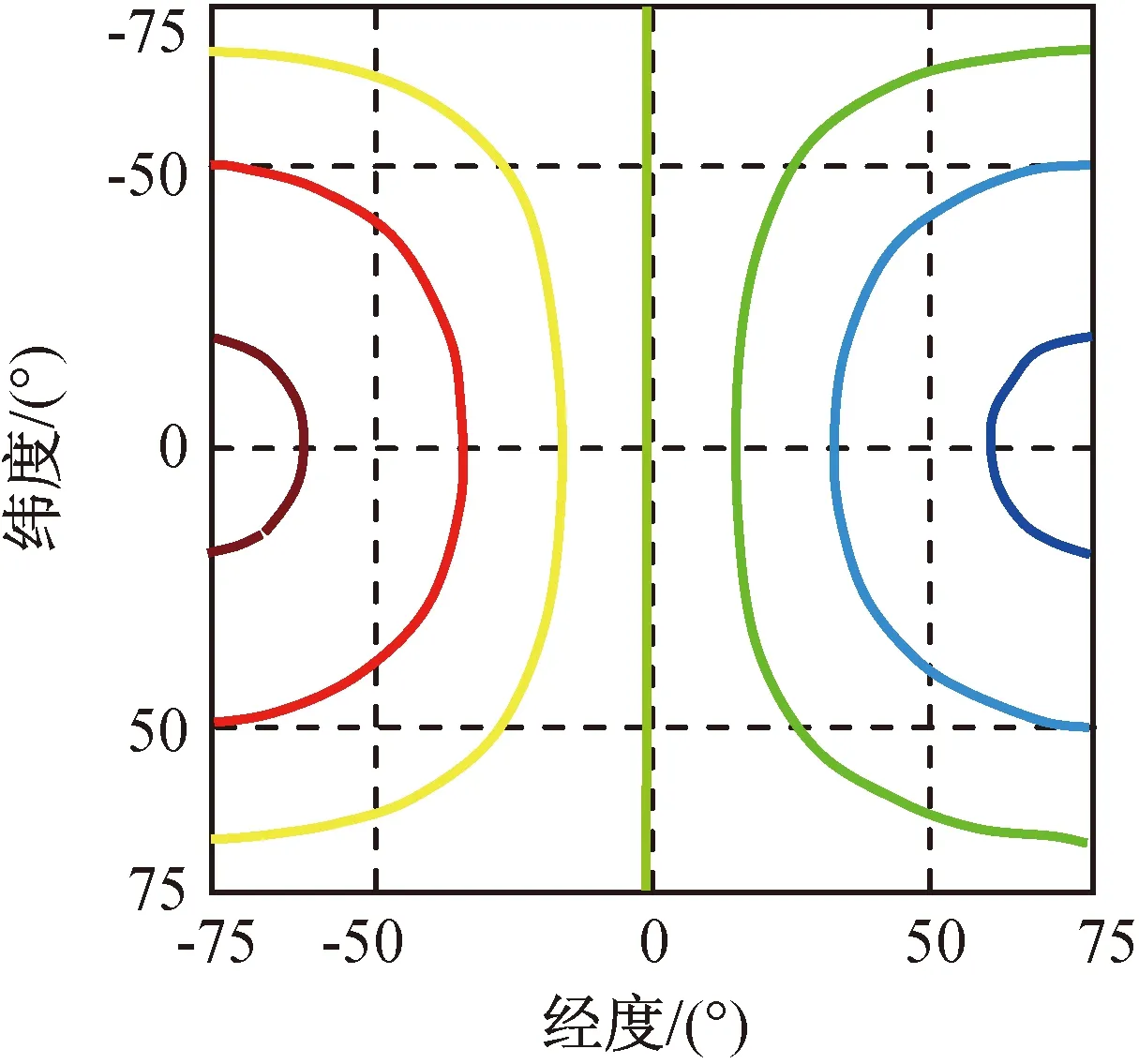
图5 地球表面等时差曲线Fig.5 Equal TDOA curves on earth

前述定位原理表明：地球表面相应的频差曲线与时差曲线的交点处即为目标所在位置。根据前文的等频差曲线的特性可知：当速度矢量方向线、地球球心与同步轨道卫星间连线的夹角θγ,e接近于π/2时，等频差曲线有较好的分布特性，这意味着同步轨道双星间的速度差矢量需尽量垂直于地球球心与同步轨道卫星间的连线。在此基础上，结合等频差曲线旋转特性可知，为在卫星星下点覆盖区域内与图5所示的地球表面的等时差线尽可能有正交的分布，同步轨道双星间的速度差矢量需尽可能平行于地球的旋转轴，在此条件下形成的地球表面的等频差曲线簇类似于如图4(c)所示。则在θγ,e=π/2，θκ,e=π/2的条件下，较理想的地球表面等时差曲线与等频差曲线的交汇如图6所示。图6中，在星下点±50°经纬度范围时差曲线与频差曲线都有较好的交汇状态，这利于定位精度的提高。

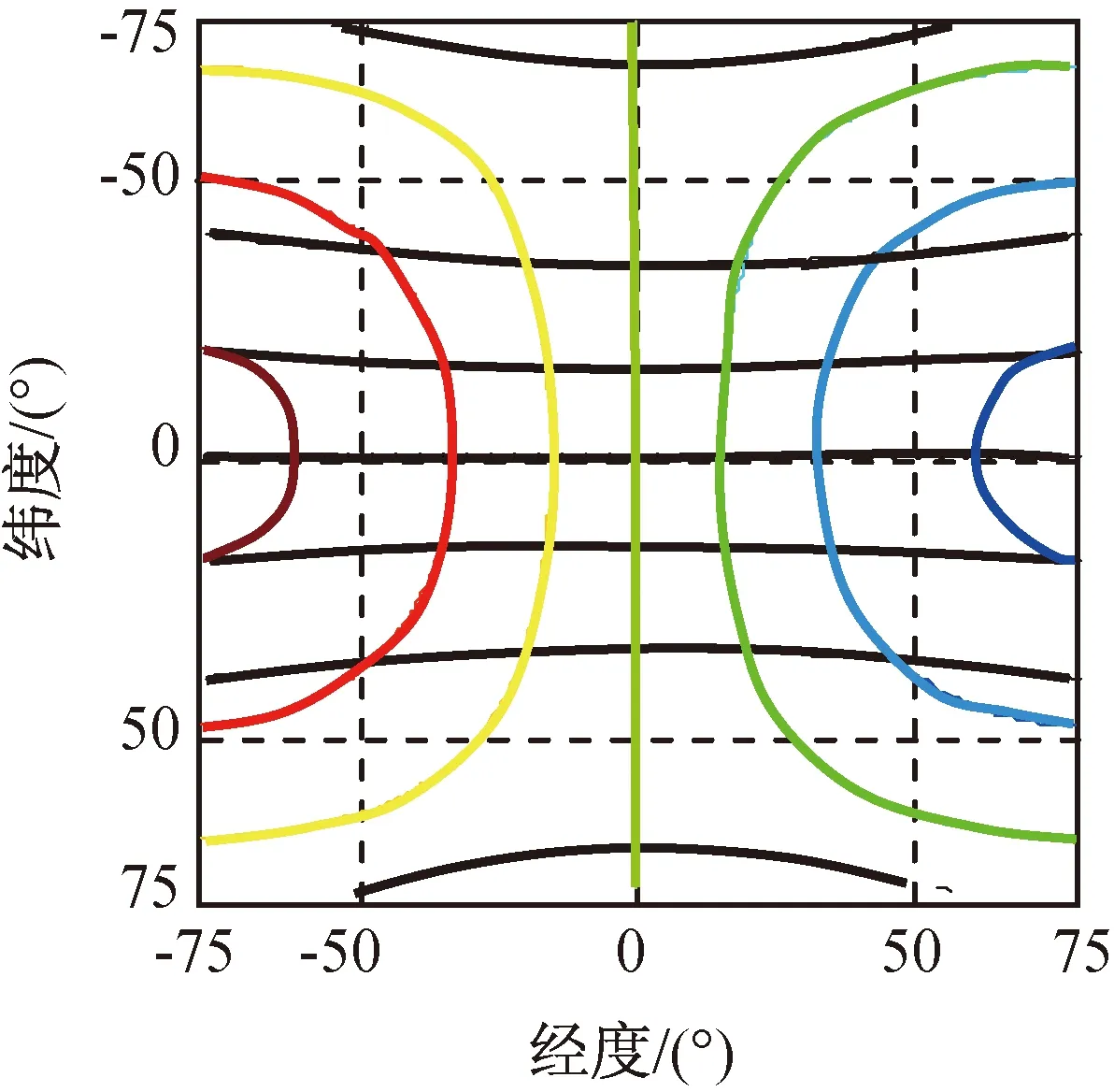
图6 较理想的等时差曲线与等频差曲线的交汇图Fig.6 Intersection of equal TDOA and FDOA curves onideal condition

在同步轨道双星对地面卫星通信类辐射源定位应用中，主星的选择是固定的，因为这与目标信号直接相关，而对副星的选择可按上述分析结果，在多个满足频率转发条件的副星中选择与主星间相对运动速度较大，且相对运动速度方向尽量平行于地球自转轴线的副星，这样的选择能使等时差线与等频差线尽可能地形成正交，从而进一步改善定位精度。另一方面，从上述分析结果并结合卫星轨道特点可知：为满足上述条件，需优先选择有相对较大轨道倾角的卫星作为副星，由此形成的相对运动速度方向会尽可能地平行于地球自转轴线。

5 仿真验证

由上述理论分析可知：同步轨道双星定位中频差曲线的形成与两颗卫星相对地面的运动速度，以及它们之间的相对经度间隔有密切的关系，本文对两颗卫星运动速度的大小比取不同数值进行仿真，在不同经度间隔条件下，比较由式(2)算得的精确频差值，以及由式(8)算得的近似频差值。因运动速度是一个矢量，故对2颗同步轨道卫星的运动方向单位向量采用空间内等概率随机方式产生。对地球表面的频差测量点在经度与纬度向均在星下点±50°范围内以1°等间隔方式均匀抽样，共由抽样点101×101个，用每个抽样点上的频差误差的绝对值除以该次仿真中的最大精确频差的绝对值表征该点频差测量的相对误差，将该次仿真中101×101个相对误差的平均值作为其频差相对误差。

在两颗同步轨道卫星速度大小比分别为1∶1，1∶3，1∶10条件下，求精确频差值与近似频差值间的误差，再按前述方法求相对误差，所得2颗卫星间不同经度间隔下频差的相对误差大小分别如图7～9所示。其中经度间隔变化范围为[1°，8°]，如两颗卫星间的经度间隔大于8°，会出现接收灵敏度问题；如经度间隔小于1°，会造成时差曲线密集问题，上述两种情况都会导致定位性能的下降，因此合理的经度间隔范围一般在两者之间。仿真中，在每个经度抽样点上进行蒙特卡罗仿真2 000次，取2 000次仿真的平均值作为最终值。

图7 卫星速度大小比1∶1时频差的相对误差Fig.7 Statistic results for relative error of FDOA (1∶1)

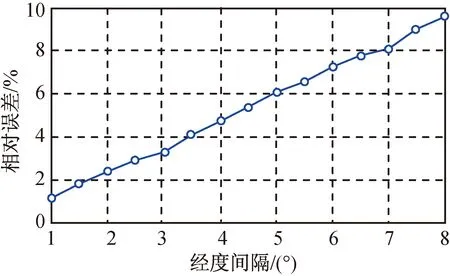
图8 卫星速度大小比1∶3时频差的相对误差Fig.8 Statistic results for relative error of FDOA (1∶3)

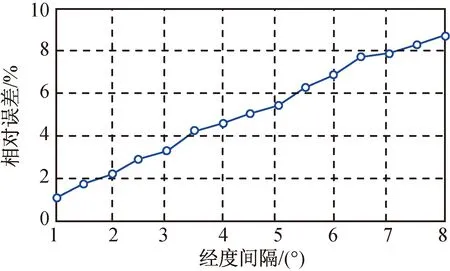
图9 卫星速度大小比1∶10时频差的相对误差Fig.9 Statistic results for relative error of FDOA (1∶10)

由仿真试验的统计结果可知：按式(8)的近似处理后，频差的相对误差随两颗同步轨道卫星间的相对经度间隔增大而变大，原因是采用角平分线矢量近似替代处理时，角度越小，近似程度越高；随着两颗同步轨道卫星间的速度大小相差越大，近似处理后，频差的相对误差越小，这是因为两颗卫星的速度相差越大，有较大运动速度的卫星在频差曲线形成过程中发挥的主导作用就越强，另一颗卫星的作用也越小，这样与单星运动产生多普勒效应的情形也更相似，故在此情况下式(8)的近似处理精度也就更高。上述仿真统计结果表明：即使在两颗同步轨道卫星速度大小一样的情况下，最大相对误差统计平均值不超过12.5%。由此可见，按式(8)所作的近似处理是较合理的。这也同时说明本文对同步轨道双星定位中等频差曲线的近似逼近和特性分析结果在统计意义上是正确的。

6 结束语

本文针对同步轨道双星对地面卫星通信类辐射源实施TDOA/FDOA定位中等频差曲线的特性进行了分析与讨论。根据实际工程应用中的约束条件，通过小角度的角平分线矢量近似方法巧妙地将

同步轨道双星定位中的等频差曲线问题转换为同步轨道单星对地形成的等多普勒曲线问题，避免了复杂的数值仿真计算过程，从而利用单颗同步轨道卫星运动产生的多普勒效应分析结果，建立了同步轨道双星定位中等频差曲线的几何模型，对定位特性进行了分析，给出了具有直观几何意义的物理解释，仿真试验结果验证了上述处理的合理性与有效性。上述研究结果一方面为同步轨道双星定位特性的研究提供了新途径，另一方面也使工程实际应用中对副星的选择和定位特性分析能快速进行，更利于对短暂持续信号的定位。

[1] 齐晓东, 潘玉平, 丁静. 民用卫星干扰源定位技术[J]. 无线电工程, 2005, 35(9): 28-29+34.

[2] 叶尚福, 孙正波, 夏畅雄, 等. 卫星干扰源双星定位技术及工程应用[M]. 北京: 国防工业出版社, 2013.

[3] 周鸿顺. 卫星干扰源的定位技术和手段[J]. 中国无线电管理, 2001(7): 30-31.

[4] 瞿文中, 叶尚福, 孙正波. 卫星干扰源定位中的误差分析与预测[J]. 电波科学学报, 2005, 20(5): 590-593+609.

[5] 陈静. 双星定位中精度空间模型的建立及应用[J]. 微计算机信息, 2010, 26(1): 160-161+159.

[6] 朱锐, 朱莉. 谈卫星干扰源双星定位法中的邻星选择[J]. 卫星与网络, 2007(8): 62-64.

[7] 刘卓然. 浅谈TDOA & FDOA卫星干扰源定位原理和实践中的几个关键因素[J]. 中国无线电, 2006(10): 23-25.

[8] 穆旭成, 张鹏, 李烨. 卫星干扰定位技术的最新发展动态[J]. 中国无线电, 2014(12): 58-59+64.

[9] 姜道安, 石荣. 航天电子侦察技术[M]. 北京: 国防工业出版社, 2016.

[10] 张勇, 盛卫东, 郭富成, 等. 低轨双星无源定位算法及定位精度分析[J]. 中国惯性技术学报, 2007, 15(2): 188-192.

Characteristic Analysis on Equal FDOA Curves for Geosynchronous Orbit Dual Satellites Location

SHI Rong, JIANG Dao-an

(Science and Technology on Electronic Information Control Laboratory, Chengdu 610036, Sichuan, China)

The equal frequency difference of arrival (FDOA) curves in geosynchronous orbit dual satellites time difference of arrival (TDOA) and FDOA location are obtained through the complicated numerical calculation in traditional methods because geometry significance cannot be revealed obviously. The engineering constrained conditions about longitude interval between major satellite and accessorial satellite were utilized in this paper. The unit vectors along earth communication equipments and satellites were approximated through the angle bisector vector. Then the problem was changed into another equivalent one, which was equal Doppler curve produced by single geosynchronous orbit satellite. Its geometry significance was definitely disclosed. The shape distribution of equal FDOA curves and integration location characteristics could be obtained quickly. The influence of equal FDOA curves and equal TDOA curves on location performance was discussed. It found that the salve satellite would be chosen among the satellites satisfying frequency transmission condition which relative motion velocity was big and the velocity direction was parallel to the earth self-rotation axis when the master satellite was fixed. It would make the equal TDOA perpendicular to the equal FDOA so the location performance could be improved. The simulation results proved the validity of this method. It is a new approach for characteristic analysis on geosynchronous orbit dual satellites location.

Geosynchronous orbit; Dual satellites location; Location by TDOA and FDOA; Passive location; Equal Doppler curves; Equal FDOA curves; Equal TDOA curves; Location performance

1006-1630(2016)06-0129-07

2016-09-18；

2016-11-12

预研共用技术基金资助(9140A21XX01XXDZX9066)

石 荣(1974—)，男，博士，研究员，主要研究方向为电子对抗、通信与雷达系统。

V443； TN971

A

10.19328/j.cnki.1006-1630.2016.06.019