离心压缩机组负载试车时振动故障的排除

文/沈阳鼓风机集团股份有限公司 郭杨

离心压缩机组负载试车时振动故障的排除

文/沈阳鼓风机集团股份有限公司 郭杨

离心压缩机广泛应用在工业的众多领域，随着工业技术水平的提高，对离心压缩机相关性能参数的要求也越来越高，这对于机组的平稳运行提出了挑战。本文就某离心压缩机组带负载试车时产生的振动故障，从振动现象出现时运行参数的变化，以及振动瀑布图、频谱图的记录入手，采用经验分析的方法，初步判断振动是由气体激振引起的，又通过理论计算和机理分析得到了进一步的证实，经过采取针对性的解决措施后，再次带负荷试车，振动故障排除了，振动值在要求范围内且运行平稳。对类似产品的设计、类似的振动故障的诊断具有借鉴作用。

离心压缩机；气体激振；密封

1 振动现象

某透平离心压缩机组，工作转速为10636rpm，一段进口压力为0.5MPa，二段出口压力为2.7MPa，三段出口压力为6.9MPa。该机组在厂内进行机械运转试车，运行平稳。机组在用户现场负荷试车时，中压缸达到设计转速后，增加负荷，当压力升到5.4MPa时，轴振动突然增大至报警值，试车被迫停止。为了查找原因，再次试车，结果与前一次（的现象）相同。利用频谱采样，发现幅值谱中除了基频（工频）成分外，还有低频成分，且低频振幅大于工频的振幅。障

表1 离心压缩机组设计及故障时的参数对比

图1 振动瀑布图

图2 频谱图

2 振动故障的原因分析

离心2 压 缩振机动发故生大障的的振原动，因一分定是析由于作用力引起的。针对于离动故故动心动2故障 压障故故 障的缩振障障机的原2动的 来的2原因 故 说原振原 因分可障振因动因分能析的动分故存分析原故在析障析因的障的作分的原用析原力因为因分：分附析加析件（如叶轮等）的不平衡力（强迫振动）；密封气体激振力（自激振动）。

2.12 .附1 加附件加的件不的平不衡平力衡力件的件加的2不.的件不1平 不的平附叶衡平不衡加轮2力平衡.力件等21力衡. 的转1附力 不动

附加平的

加件衡部

件的力件的不，不平在平衡加衡力工力的过程中，一定会存在不平衡量。当加件的不平衡力

转子转动时，不平衡量就会对转子有一个交变的力的作用，这个力被称为不平衡力。这种振动形式属于强迫振动，即系统在外界激振下所产生的振动。不平衡力作用下的转子的动力学公式，可以简写为：其中：ω

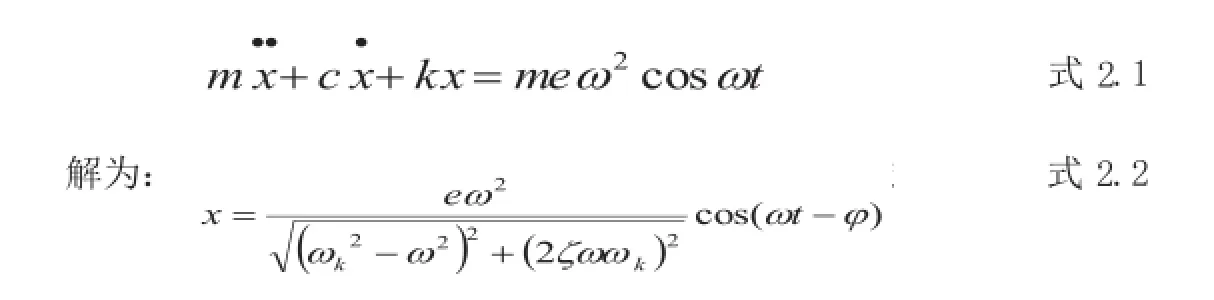
——转子角速，ωk——转子固有频率，φ——相位差。由上可知

：当转子的转速等于转子的固有频率（一般被称为临界转速）时，振幅值会很大（由于阻尼存在；若系统没有阻尼则振幅为无穷大），此时，结构发生共振。为了保证转子的平稳运行，工作转速与转子的临界转速之间必须有一定的隔离欲度，以来满足转子的稳定运转需要。根据2.

上2密述封的气事体故激机振组力的情况描述：厂内离心压缩机机械运转试验，机组运行平稳；在现场，机械运转试验和空载试验，机组运行平稳。API中提到，密封的作用力，对于转子不平衡力的分析，是可以忽略的。所以，完全可以由转子的机械运转试验和空载试车来判断结构发生的较大的振动，是否是由于不平衡量引起的。由此，可以得出结论：导致机组振动过大的原因，不是由于不平衡响应引起的。2.2 密封气体激振力3 振动故障的理论透平机械

转子中的密封在防止流体泄漏的同时，还会产生重要的流体激

振力，从而使转子的振动过大，影响3转.1子 转的子稳失定稳性（的平定稳义运和衡行）。气流激振属于自激振动范围（系统受到其自身运动诱发出来的激励作用而产生的、维持的振动）。此时，系统包含有补充能量的能源。这种振动不能由动平衡的方法消除。密封间隙气体力与设备工作介质的压力和负荷变化相关。密封气体激振失稳振动有一个门槛负荷，超过此负荷，立即激发气体振动；相反，气流激振在小于某一负荷下会消失。气流激振在负荷增加过程中，易重复发生。另外，气流激振的振动频率等于或者略高于一阶临界转速。

由此，可以得出气体密封力的特点：（1）随着介质的压力的增加，振动越大。（2）密封前后的压差越大振动越大。（3）密封的间隙越小，越易发生振动。（4）转子的涡动频率为第一阶临界转速。

表2 密封气体激振情况描述

根据现场的描述：机械运转试车时，运行平稳；现场有介质输入时，进出口的压力达到一定的值时，突然振动过大。机械运转试验，是指在机组没有介质情况下进行的，密封内的气体激振力也就不存在。当现场有介质的输入时，密封的间隙内就会有密封气体激振力的产生，而且随着压差的增加突然振动变大；当减小压差时，机组的振动消失。通过频谱图的测试也可以看出，振动的频率在一阶临界转速处。这些现象与密封气体激振导致的失稳情况很一致，所以，可以得出结论该机组的振动过大，是由于密封气体激振引起的。

3 振动故障的理论计算及机理分析

3.1 转子失稳的定义和衡量

当转子系统受到瞬时的一个激励，若系统的阻尼足够大，则这种自由振动可以很快的就衰减，转子系统是稳定；若系统的阻尼不足，则系统的自由振动会越来越大，转子系统失稳。

选取一个单自由度系统来说明一下问题。

转子系统的自由振动方程为：

其中m为质量；c为系统的阻尼；k为系统的刚度；x为转子的位移。一般将连续两个振幅的比值取对数，

该数被称为对数衰减率，通过对数衰减率的正或者负就可以来描述转子系统是稳定还是不稳定的了：

转子的自由振动随时间可能的变化曲线见图3和图4转子的自由振动时，转子会按照系统的固有频率来做周期行的运动，由于阻尼的存在，周期运动的幅值会改变的。若系统是稳定的，即阻尼力较大，则振动幅值逐渐衰减；若系统不稳定，即阻尼力做功不能消耗掉系统内部的力，则振动幅值会越来越大。

图3 稳定系统的自由振动迅速衰减

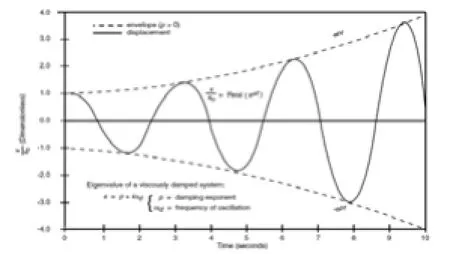
图4 不稳定系统的自由振动迅速增加

API617相关标准章节中规定，对数衰减率应该大于0.1，则转子系统的稳定性满足要求。

3.2 理论计算

稳定性计算结果可以看出：发生激振问题的机组，利用软件计算的结果，对数衰减率小于API617中的要求，即大于0.1，所以可以得出结论，该产品存在发生气体激振的危险，理论计算稳定性不满足要求。

3.3 振动机理分析

转子受到外界的干扰时，转子除了绕自身轴线转动外，还可能以一定的角速度绕平衡位置涡动。密封气体激振力的特点是，一个方向的位移可以引起两个方向的力的作用，即合力并不是沿着位移的方向的。所以，通过主动力系数和交叉动力系数两种参数来表达密封气体激振力的这个特点。当转子绕轴心做小挠度运动时，其动力方程可以表示成：

其中K、C为密封的主动力系数；k、c为密封的交叉动力系数。

图5 轴颈涡动受力示意图

图6 轴蜂窝密封图片

其中切向力是推动转子进行涡动的力，一般通过转子—轴承—密封系统的有效阻尼和有效刚度来进行定义，来量化结构的稳定特性：

由3.2，3.3和3.4式可知：若想提高转子的稳定性可以通过改善刚度、阻尼以及密封的交叉耦合刚度。对应于轴承、密封和转子的结构这几个方面来进行完善。

密封结构的更改，通过改变密封的形式：

——提高密封的阻尼；

——减小密封的交叉耦合刚度。

减小密封的气体激振力：减小密封的进口气流周向速度

——密封进口处理。

轴承的影响：

——增加轴承的阻尼。

转子结构的影响：

——提高转子的刚性。

4 采取的措施

大型离心式压缩机组的密封常用迷宫式密封（又称梳齿密封）。气体在迷宫密封中的流动是一种复杂的三维流动。当转子因挠曲、偏磨、不同心或旋转产生涡动运动时，密封腔内的周向间隙将会不均匀，即使密封腔内人口处的压力周向分布是均匀的，在密封腔的出口处也会形成不均匀的周向压力分布，从而产生一个作用于转子上的合力，此激振力会导致转子运动失稳，发生异常振动。

4.1 密封结构的改进—蜂窝密封代替迷宫密封

为了增加密封的稳定性，国内外经常采用的方式是发展阻尼密封技术即蜂窝密封代替迷宫密封。蜂窝密封是一种常见的阻尼密封，其结构特点是具有光滑的转子和粗糙的定子面。由于粗糙度，使得这种密封拥有比迷宫密封大的阻尼系数，同时还能削弱密封内的周向速度，进而减小了密封的交叉刚度。这就通过两个方面：增加密封内部的阻尼和减小密封的交叉耦合刚度，两方面都可以提高密封的有效阻尼，从而提高转子的稳定性。是使用了蜂窝密封代替原来的迷宫密封，而解决了密封气体激振问题。

4.2 减小密封进口气流的周向速度

在叶轮机械中，由于各部件的旋转作用或设计时就带有预旋，密封进气口的气流都会带有不同程度的周向速度。密封内较大的周向速度会对转子的稳定性产生显著的影响。这是因为进口预旋对密封内周向速度的发展起着重要的作用，而周向速度的增大，会加大密封系统的交叉耦合刚度，根据式3.4可知，交叉刚度的增加，有效阻尼就会相应的减小。

5 结论

应用经验分析和理论计算机理分析两种方法，成功地排除了某离心压缩机组用户现场带负荷试车时产生的振动故障。首先针对试车过程的运行参数，振动出现时运行参数的变化以及频谱图的记录，采用经验分析的方法，初步诊断为机组振动故障的原因是密封气体激振引起了转子的失稳而造成的;又应用理论计算和振动机理的分析，进一步证实了经验分析的结论。通过采取改变密封的进口速度方向和密封的形式等有针对性的解决措施，再次带负荷试车，振动数值符合要求，机组运行平稳。

实践证明，本文的经验分析和理论计算诊断出的振动原因是准确的，采用的解决措施是恰当的，有效地解决了气体激振所造成的机组振动故障，从而保证离心压缩机组正常平稳运转，为类似产品的设计、类似的振动故障的诊断具有借鉴作用。

责编/魏晓文

[1] API Standard 684, 2005, "Tutorial on Rotordynamics: Lateral Critical, Unbalancing Response, Stability, Train Torsional and Rotor Balancing," Second Edition, American Petroleum Institute, Washington, D.C.

[2] 李军，晏鑫，丰振平，等.透平机械阻尼密封技术及其转子动力特性研究进展[J].热力透平，2008-10-8.

[3]何立东，夏松波.转子密封系统流体激振及其减振技术研究简评[J].振动工程学报，1999-12.

[4]张克峰，杨爱学.气流激振对离心压缩机的影响及其消除对策[J].大氮肥，2006-4.

[5]何立东，袁新尹.新蜂窝密封减振激励的研究实验[J].中国电机工程学报，2001-10.

[6]刘士学，方先清.透平压缩机强度与振动[M].西安交通大学，1996.

该项目2013年为沈鼓集团“讲理想、比贡献”项目，并评为一等奖。