改进的Dijkstra算法在多点最优路径组合中的应用——以大学生出游App为例

唐彬文,卓雨嘉,陈小青

集美大学诚毅学院,福建厦门361021

改进的Dijkstra算法在多点最优路径组合中的应用
——以大学生出游App为例

唐彬文,卓雨嘉,陈小青

集美大学诚毅学院,福建厦门361021

随着我国经济发展和社会进步，人们满足了日益丰富的物质生活的同时更多追求精神上愉悦，因此，旅游业方兴未艾。面对如火如荼的旅游在线平台的发展，如何为游客提供多点组合的最优观光路径，成为当下迫切的需求。本文摈弃传统的点对点导航模式，利用改进的Dijkstra算法设计和开发了一个具有旅游线路推荐功能的大学生出游App，充分利用现有的移动平台载体，为游客方便快捷地规划合理的游览线路。

Dijkstra算法;旅游;App

Dijkstra方法是目前公认最好的最短路径计算方法，是由Dijkstra于1959年提出的。Dijkstra算法是典型最短路径算法，用于计算一个节点到其他所有节点的最短路径[1]。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法的基本思想是源点V0出发，逐步向外扩张，寻找最短路径直至终点Vn的过程。经典的Dijkstra算法只能分别计算出源点（出发点）到各个点的最短路径。但是现实的旅游线路需求不是点对点的，经常是多点的集合。那么针对多点最优路径组合，经典的Dijkstra算法是无法计算的。本项目运用面向对象的程序设计思想，前端设计采用Html5风格设计，后台开发采用php+mysql+apache组合，最后使用Cordova进行App的封装。App核心模块功能旅游线路推荐模块是通过改进Dijkstra算法，经过多次循环嵌套、迭代和数组遍历等方法推算出多点的最优路径组合。

1 算法思想

1.1 前提假设

（1）所有节点组成的集合图是赋权无向图。即Vn-1到Vn之间的距离与Vn到Vn-1之间的距离相等；

（2）V0为源点（出发点）；

（3）所有路径的组合必须回到源点，形成回路；

（4）为了便于输出结果的解读，算例使用的节点个数为5，包括源点V0。

1.2 算法逻辑

（1）经典Dijkstra算法的引入；

（2）改进算法，分别计算出包括源点在内的所有点之间的最短路径；

（3）将最短路径值和最短路径经过的点集分别存入多维数组Djz和Ejz；

（4）根据游客选择的景点（包括源点）构成一个点集Vx，VxÎVn。(n为景点总数，n包括源点)；

（5）使用循环迭代判断Vi-1→Vi之间的路径是否包括第三点j(iÎx;jÎx)，如果有则从Vx中剔除；

（6）最终得到的点集Vm就为最优路径组合(mÎx)；

（7）m个节点依次排列形成组合（V0→V1→V2→¼→Vm），按照点对点组合分别从Djz和Ejz获取值，组成最优路径值和最优路径组合点集。

2 算法实现

2.1 算法案例

算法通过实测30多个算例，能够满足20个节点以内的最优组合计算。本项目为周边游项目（短期旅游项目），为了良好的用户体验和论文阐述清晰，便以厦门地区四个主要景点的实际距离赋权为算例。图1是以四个景点构建的赋权无向图。并将节点之间的距离存入初始矩阵。2.2构建类计算最短路径和最短路径经过的点集

图1 赋权无向图Fig.1 Undirected weighted graph

图2 初始矩阵Fig.2 The initial matrix

2.2.1 改进的Dijkstra算法

2.2.2 初始算法解释

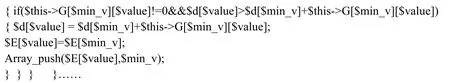
2.2.3 最优点集算法解释

①用数组$V存放包括源点在内的所有节点；

②数组遍历距离源点最近的节点X，并从数组$V中，去除该节点;

③比较其他点Y与源点的距离$d[Y]是否大于$d[X]（X与源点距离）+$G[X][Y](节点X与Y的距离)，是则用该距离存入最短路径数组$d,同时更新最短路径组合覆盖原有的二维数组$E[$value]，并将该节点的编号添加在$E[$value]的尾部。

④循环以上操作则可以得出：

$d=Array([0]=>0[1]=>5[2]=>3[3]=>1[4]=>6)

$E=Array([0]=>Array([0]=>0)[1]=>Array([0]=>0[1]=>2)[2]=>Array([0]=>0)[3]=> Array([0]=>0)[4]=>Array([0]=>0[1]=>2[2]=>1))

例如：V0到V4的最短距离为：$d[4]=6；经过的路径为$E[4]=V0→V2→V1。

2.2.4 节点间最短路径值和最短路径经过节点集的计算

多源点算法解释：分别以0～4，五个节点为源点求出与其他点的最短距离存入二维数组$Djz，和最短路径节点集存入三维数组$Ejz。

2.2.5 结果输出及解释

$Djz为：

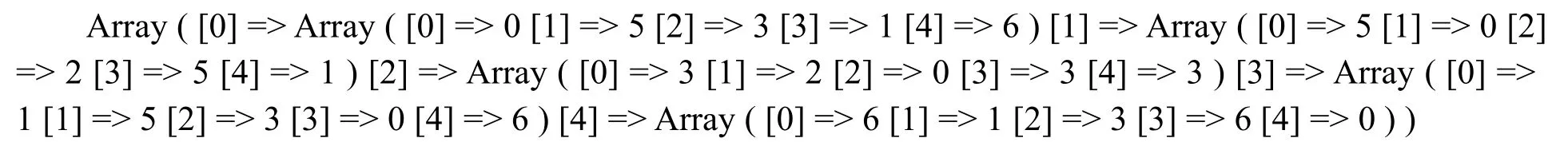
以上值转化为多点最优矩阵为：

图3 最优矩阵Fig.3 Optimal matrix

三维数组$Ejz为：

输出结果解释：例如$Ejz[0][1]=(0,2),表示到达V1的最短路径点集为(V0,V2)。

2.3 多点最优组合计算

2.3.1 最短距离算法

算法解释：三维数组$Ejz[x][y][i]，x与y表示两个节点，第三维i表示它们之间最短路径经过的节点集。用循环计算出两点之间的最短路径$sum。

2.3.2 交叉节点剔除算法

2.3.3 算法解释

(1)根据游客提交的景点组合作为节点存入数组$Vs，$Vs=(0,a,b,c,d),0为源点，a,b,c,d为景点对应的节点（0为源点为必选项，其余节点可任意组合）；

(2)将$Vs付给$Os，因为$Vs将进行删除重复节点操作，需要一个完整的初始值做重复的遍历；故定义$Us数组存放经过删除操作的$Vs数组；

(3)通过三层嵌套的数组迭代，剔除路径交叉时的重复节点。依次剔除$Vs中两个节点的x,y，并获取对应三维数组$Ejz[x][y]的值，遍历剩余节点数组$Us，判断是否有节点与$Ejz[x][y]中的节点重复，有将其从$Vs中删除。

(4)以上代码段若$Vs=Array(0,1,2,3,4)，输出结果为Array([0]=>0[1]=>3[2]=>4)，

即$newVs=Array(0,3,4)。

2.3.4 多点最优路径组合算法

2.3.5 算法解释

(1)方法best()用于计算最优的距离和路径，假设从源点V0出发并回到源点V0；

(2)调用三维数组$Ejz，用for循环分别将$new Vs中的V0→V1，V1→V2，¼Vn-2→Vn-1的节点距离和节点路径累加存入总距离$sum all和节点集合二维数组$programme；

(3)调用三维数组$Ejz，将Vn-1→V0两节点的最短距离和最短路径节点集合分别加入总距离$sum all和节点集合二维数组$programme。

2.4 多点最优路径组合计算结果

(1)Array(0,1,2,3,4)为选中所有的景点，得出最短路径为13；

(2)最优路径节点集合为：V0→V3→V2→V1→V4→V1→V2→V0

(3)因为节点V2属于重复节点，故(0,1,3)和(0,1,2,3)两种组合得到结果是一样的。

3 结束语

通过利用PHP+MYSQL+APACHE技术设计和开发出了一个以大学生及其家人团体为目标客户群的App，希望以此App构建的平台能给那些计划旅行，对旅游线路组合信息检索具有需求的学生或家长用户提供帮助。程序内核是通过改进Dijkstra算法构建多点最优路径组合模型，并具体实现其应用功能。经过实测，能够满足20个节点以内的多点赋权无向图的优化组合运算。不仅在技术上取得突破，而且有效弥补了App应用在该领域的空缺。

[1]Hofner P,Moller B.Dijkstra,FloydandWarshallmeetKleene[J].FormalAspectsof Computing,2012,24(4-6):459-476

[2]Chang JR,Jheng YH,Chang CH,et al.An Efficient Algorithm for Vehicle Guidance Combining Dijkstra and A* Algorithm with Fuzzy Inference Theory[J].Journal of Internet Technology,2015,16(2):189-200

[3]Payette S.Hopper and Dijkstra:Crisis,Revolution,and the Future of Programming[J].IEEE Annals of the History of Computing,2014,36(4):64-73

[4]Daylight EG,Wirth N,Hoare T,et al.The Dawn of Software Engineering:From Turing to Dijkstra[J].IEEE Annals of the History of Computing,2014,36(1):71-73

[5]王树西,吴政学.改进的Dijkstra最短路径算法及其应用研究[J].计算机科学,2012,39(5):223-228

[6]潘若愚,褚伟,杨善林.基于Dijkstra-PD-ACO算法的大城市公交线路优化与评价方法研究[J].中国管理科学,2015,23(9):106-115

The Application of Improved Dijkstra Algorithm in the Selection for Optimal Multi-point Traveling Routes－Taking the travelingApp for college students as a case

TANG Bin-wen,ZHUO Yu-jia,CHEN Xiao-qing
Chengyi College/Jimei University,Xiamen 361021,China

Along with the economical development and social progress in our country,people not only meet the increasingly rich material life but also pursuit the more spiritual pleasure,therefore,tourism industry is in the ascendant.In the face of the flourishing tourism online platform development,it is pressing how to provide visitors with more combination of the optimal traveling routes.Away from the traditional pattern of point-to-point navigation,this paper used the improved Dijkstra algorithm to design and develop an App with the recommending function for college students to fully use the existing mobile platform carriers to provide reasonable routes for tourists conveniently and quickly.

Dijkstra algorithm;traveling;App

U284.37

A

1000-2324(2016)06-0927-05

2016-02-10

2016-03-05

福建省2015年省级大学生创新创业训练计划项目:大学生出游网络服务平台(201513471030)

唐彬文(1982-),男,硕士,讲师,研究方向:管理信息系统和电子商务.E-mail:tom414@jmu.edu.cn