土层剪切波速与埋深关系统计分析和应用

贺为民 刘明军 杨 杰

(中国地震局地球物理勘探中心，郑州 450002)

土层剪切波速与埋深关系统计分析和应用

贺为民 刘明军 杨 杰

(中国地震局地球物理勘探中心，郑州 450002)

一般认为土层剪切波速与埋深关系的回归公式主要用于对当地土层剪切波速值的初步估计。为了提高钻孔波速测试数据的应用价值，基于土层剪切波速与埋深关系的主要数学模型及其拟合参数，推导了场地覆盖层厚度计算公式、 等效剪切波速计算公式和时深转换中反射波组埋深计算公式。以河南省长垣县场地为例，采用上述新公式计算获得的场地覆盖层厚度值、 等效剪切波速值可满足工程需要。并提出应用这些新公式的步骤为： 1)依据场地相关资料划分地震工程地质单元； 2) 对同一个地震工程地质单元内的钻孔波速测试数据进行统计分析，综合判别和选择土层波速与埋深统计关系的数学模型及其拟合参数； 3)将选择的数学模型的拟合参数分别代入上述的新公式，即可分别获得场地覆盖层厚度、 等效剪切波速或地层反射波组埋深。

等效剪切波速 场地覆盖层厚度 时深转换 地震工程

0 引言

土层剪切波速是地震工程中的重要参数之一，在中国建筑的场地类别划分(彭艳菊等，2009； 黄雅虹等，2010)、 饱和地基土地震液化判别(曹振中等，2010； 袁晓铭等，2011)、 土层地震反应分析(李小军，2006)、 隐伏(活)断层横波勘探中的时深转换(刘保金等，2008； 许强等，2009)等方面得到了应用。许多学者(陈国兴等，1998； 刘红帅等，2010； 邱志刚等，2011)在整理土层剪切波速测试数据的基础上，对土层剪切波速与埋深关系进行了统计分析，常用的回归公式数学模型有3个： 线性函数模型、 一元二次函数模型和幂函数模型，获得的模型参数(拟合参数)带有明显的地域土质特征。一般认为这些剪切波速与埋深关系的回归公式主要用于对当地土层剪切波速值的初步估计。然而，在同一个地震工程地质单元内，如果有较多钻孔的剪切波速测试数据，对其进行统计分析获得的回归公式不但可以用来计算统计埋深区间上的土层剪切波速值，而且可以计算场地覆盖层厚度和统计埋深区间上任意深度段土层剪切波速平均值(含等效剪切波速值)，这对于当地一般工程建筑的场地类别划分和隐伏(活)断层横波地震勘探反射时间剖面与深度剖面之间的转换具有实用价值。本文以豫东平原长垣县主城区地震小区划场地中的钻孔土层剪切波速测试数据为例，利用前述3个数学模型以及一元三次函数模型和一元四次函数模型，通过统计分析建立了该场地土层剪切波速与埋深关系的回归公式，在此基础上，推导了场地覆盖层厚度、 土层剪切波速平均值(含等效剪切波速)、 时深转换中反射波组埋深等相关计算公式，为提高土层剪切波速与埋深关系的回归公式的实用价值提出了具体方法和步骤。

1 剪切波速与埋深关系统计分析

1.1 地震工程地质概况

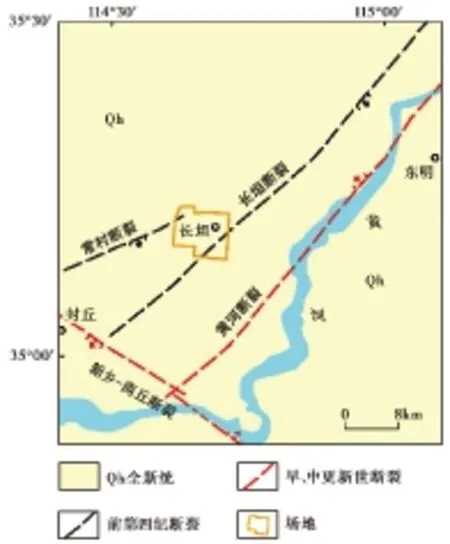
图1 长垣县地质构造略图Fig. 1 Geological sketch map of Changyuan County.

长垣县主城区位于河南省豫东平原东北部，东南距黄河17km(图1)。在长垣县主城区地震小区划项目中，场地面积52.0km2，该场地地貌单元属黄河冲积平原，地形平坦，相对高差0.5～2.0m。场地地下水类型为潜水，水位埋深8.0～10.0m，水位年变幅1.0～1.5m。钻探揭示(图2)，该场地土层分布比较稳定连续，层状结构特征明显，在埋深0～27m范围内，土层岩性主要为黄褐—灰黄色稍密—中密粉土、 黄褐色可塑粉质黏土，夹黄褐色稍密粉砂； 在埋深27～75m范围内，土层岩性主要为浅灰黄色中密粉砂、 黄褐色中密—密实粉土、 浅灰黄色中密细砂、 黄褐色硬塑粉质黏土； 在埋深75～100m范围内，土层岩性主要为浅灰黄色密实细砂和黄褐色硬塑粉质黏土。

剪切波速测试采用XG-I型悬挂式波速测试仪，测点间距1.0m，测试钻孔64个，其中100m深度钻孔20个。结果表明，长垣县主城区场地等效剪切波速最小值为192m/s，最大值为178m/s，平均值为184.2m/s； 场地覆盖层厚度最小值为89m，最大值为94m，平均值为91.6m。依据现行建筑抗震设计规范(GB50011-2010)，建筑的场地类别为Ⅲ类。长垣县主城区整个场地位于同一个地貌单元，地层地质年代和成因类型相同，场地地震工程地质条件与水文地质条件相同，可划为同一个地震工程地质单元。

1.2 统计数学模型

目前，许多学者(陈国兴等，1998； 刘红帅等，2010； 邱志刚等，2011)对土层剪切波速与埋深关系进行回归分析时常用的数学模型为

(1)

(2)

(3)

式(1)—(3)中： v为土层剪切波速(m/s)，h为土层埋深(m)，a、 b、 c、 e、 f、 g、 i为拟合参数，h1、 h2分别为统计埋深区间的上限值(m)和下限值(m)。式(1)为线性函数模型，式(2)为一元二次函数模型，式(3)为幂函数模型。

从数学角度来看，线性函数模型不适用于土层剪切波速与埋深关系散点图(曲线)有拐点的情况，一元二次函数模型和幂函数模型不适用于散点图(曲线)上存在2个拐点的情况。为适用于场地土层剪切波速与埋深关系散点图(曲线)存在2个以上拐点的情况，增加一元三次函数模型、 一元四次函数模型分别为

(4)

(5)

式(4)、(5)中： j、 k、 l、 p、 q、 r、 s、 u、 w为拟合参数。

1.3 统计结果初步分析

长垣县主城区场地实测剪切波速与埋深关系散点图和钻孔综合柱状图见图2。其中，散点图在埋深27m和75m附近存在拐点，分别对应于土层结构为黄褐色中密粉土与浅灰黄色密实粉砂的分层界面和黄褐色硬塑粉质黏土与浅灰黄色密实细砂的分层界面，是土层层状结构的具体反映。为了获得最适合本场地土质特征和使用目的的数学模型及其拟合参数，统计分析时采用试算法，利用Origin9软件对上述各个数学模型分别在整个埋深区间[0，98]和分段埋深区间[0，20]以及区间[75，98]上进行了回归分析，其结果见表1，在埋深区间[0，98]上的回归曲线见图2。

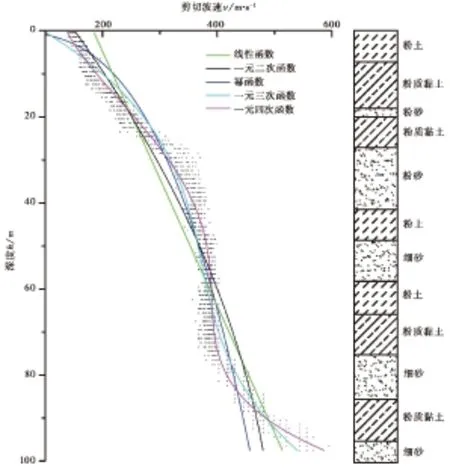
图2 长垣县土层剪切波速与埋深关系图和钻孔综合柱状图Fig. 2 The relationship between shear wave velocity and depth of soil layer，integrated histogram of borehole in Changyuan County.

表1 长垣县土层剪切波速与埋深关系拟合参数统计表

Table1 Statistics of parameters of fitting relationship between shear wave velocity and depth of soil layer in Changyuan County

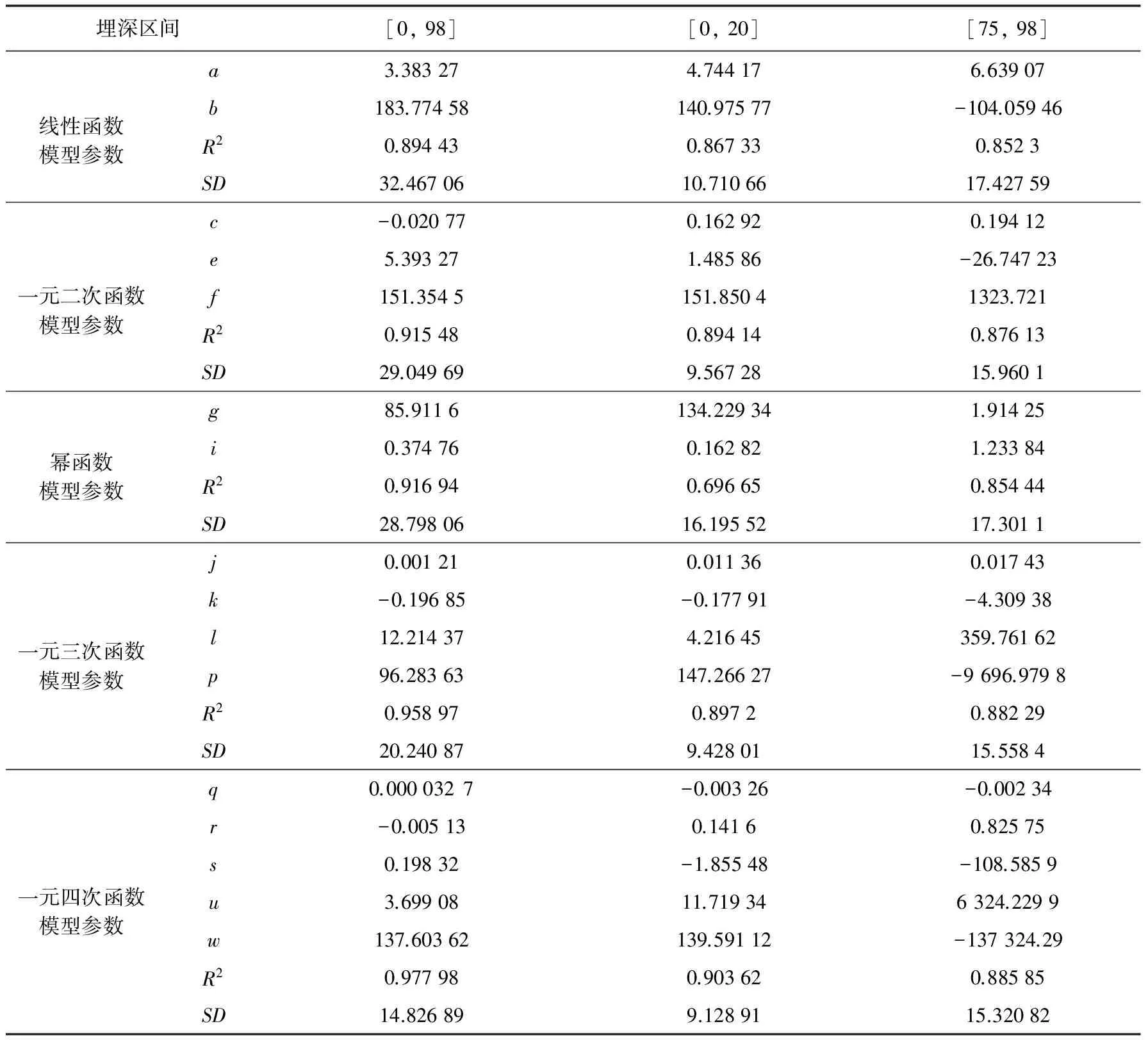
埋深区间[0，98][0，20][75，98]线性函数模型参数a3．383274．744176．63907b183．77458140．97577-104．05946R20．894430．867330．8523SD32．4670610．7106617．42759一元二次函数模型参数c-0．020770．162920．19412e5．393271．48586-26．74723f151．3545151．85041323．721R20．915480．894140．87613SD29．049699．5672815．9601幂函数模型参数g85．9116134．229341．91425i0．374760．162821．23384R20．916940．696650．85444SD28．7980616．1955217．3011一元三次函数模型参数j0．001210．011360．01743k-0．19685-0．17791-4．30938l12．214374．21645359．76162p96．28363147．26627-9696．9798R20．958970．89720．88229SD20．240879．4280115．5584一元四次函数模型参数q0．0000327-0．00326-0．00234r-0．005130．14160．82575s0．19832-1．85548-108．5859u3．6990811．719346324．2299w137．60362139．59112-137324．29R20．977980．903620．88585SD14．826899．1289115．32082

表1中，R2值是校正决定系数(Adj. R-Square)，相当于Excel中为表述拟合优度而引入的决定系数R2值(钟晓鸣等，2009)。部分学者(刘红帅等，2010)仅采用R2来检验这些回归关系对观测数据的拟合程度，用来度量总体回归效果的优劣。然而，由表1 可知，埋深区间[0，98]上的校正决定系数R2值普遍高于埋深区间[0，20]和埋深区间[75，98]上的R2值，但是其线性函数拟合曲线、 一元二次函数拟合曲线和幂函数拟合曲线有多处明显偏离图1 中土层剪切波速散点的分布区域，而埋深区间[0，20]和埋深区间[75，98]上的拟合曲线皆与图1 中土层剪切波速散点图吻合程度较高。可见仅采用校正决定系数R2来判定回归效果存在误判的情况。

表1中，SD值是标准差(Root-MSE)。从图2 中各条拟合曲线与土层剪切波速散点图吻合程度来看，SD值可以16为界，SD值>16的拟合曲线与土层剪切波速散点图吻合程度较差，包括埋深区间[0，98]上的线性函数拟合曲线、 一元二次函数拟合曲线、 幂函数拟合曲线、 一元三次函数拟合曲线、 埋深区间[0，20]上的幂函数拟合曲线； 而SD值<16的拟合曲线与土层剪切波速散点图吻合程度较好。

残差与自变量关系散点图(图3)表明，在埋深区间[0，98]上的线性函数模型(图2a)、 一元二次函数模型、 幂函数模型以及在埋深区间[0，20]上的幂函数模型的残差幅值范围较大(-60～110)，并且可看到残差值随自变量有一定的变化规律，说明模型不稳定(拟合结果较差)； 而在埋深区间[0，20]上的一元四次函数模型(图2b)以及其他模型残差幅值范围较小(-25～30)，并且残差散点基本呈杂乱无序分布，说明残差值基本不随自变量变化，模型是比较稳定的(拟合结果较好)。

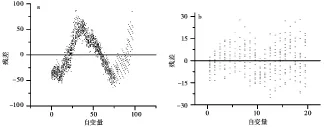
图3 残差与自变量关系散点图Fig. 3 The relationship between regular residual and independent variable.a 线性函数模型，埋深区间[0，98]； b 一元四次函数模型，埋深区间[0，20]

2 场地覆盖层厚度计算公式推导与应用

现行建筑抗震设计规范(GB50011-2010)规定，在一般情况下场地覆盖层厚度为从地面到剪切波速>500m/s 且其下卧层剪切波速均≥500m/s 的土层顶面的距离。因为前述土层剪切波速与埋深关系表达式在统计埋深区间内均为增函数，故取剪切波速v为500m/s，分别代入式(1)—(5)，即可分别获得基于线性函数模型、 一元二次函数模型、 幂函数模型、 一元三次函数模型、 一元四次函数模型的场地覆盖层厚度H(m)计算公式或方程为

(6)

(7)

(8)

jH3+kH2+lH+p-500=0

(9)

qH4+rH3+sH2+uH+w-500=0

(10)

方程(9)、 (10)分别为一元三次方程和一元四次方程，虽然有求根公式(范盛金，1989)，但比较复杂； 可采用迭代法求解，不再赘述。

将表1 中各个模型的拟合参数分别代入式(6)、 (7)、 (8)和方程(9)、 (10)中，可得长垣县主城区场地覆盖层厚度计算值(表2)。

表2 长垣县场地覆盖层厚度计算结果

Table2 Calculation results of the thickness of ground cover layer in Changyuan County

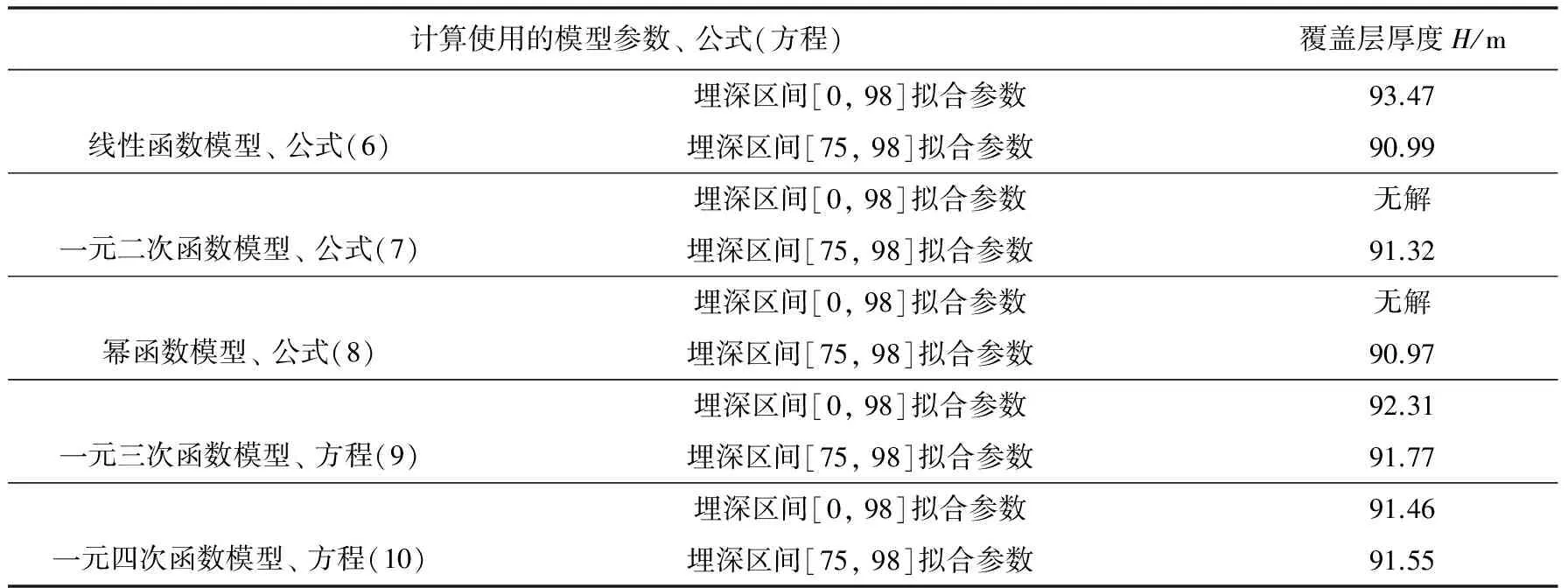
计算使用的模型参数、公式(方程)覆盖层厚度H/m线性函数模型、公式(6)埋深区间[0，98]拟合参数93．47埋深区间[75，98]拟合参数90．99一元二次函数模型、公式(7)埋深区间[0，98]拟合参数无解埋深区间[75，98]拟合参数91．32幂函数模型、公式(8)埋深区间[0，98]拟合参数无解埋深区间[75，98]拟合参数90．97一元三次函数模型、方程(9)埋深区间[0，98]拟合参数92．31埋深区间[75，98]拟合参数91．77一元四次函数模型、方程(10)埋深区间[0，98]拟合参数91．46埋深区间[75，98]拟合参数91．55

采用上述公式或方程时，获得的场地覆盖层厚度计算值一定要结合其所属的统计埋深区间[h1，h2]等因素来判别取舍。例如，式(7)实际上为一元二次方程的2个根，将表1 中一元二次函数模型在埋深区间[75，98]上的拟合参数代入式(7)，可得2个根分别为46.5m和91.32m； 显然，舍去不在埋深区间[75，98]上的根46.5m，而取91.32m为场地覆盖层厚度。再如，表1 中一元二次函数模型在统计埋深区间[0，98]上的校正决定系数R2高达0.915,48，采用式(7)求得的2个根分别为121.58m和138.04m，皆不在埋深区间[0，98]上，即无解。这表明在埋深区间[0，98]上一元二次函数模型不适用于表达长垣县土层剪切波速与埋深关系，也表明仅采用校正决定系数R2来判别回归效果存在缺陷； 采用幂函数模型在埋深区间[0，98]上的拟合参数和式(8)计算场地覆盖层厚度也出现无解即计算值溢出于埋深区间[0，98]的现象； 其原因是，从几何图形上来看，一元二次函数曲线和幂函数曲线上仅有1个拐点，因此，一元二次函数和幂函数不能用来准确描述具有2个或2个以上拐点的曲线，而从图2 可以看出，在埋深区间[0，98]上，土层剪切波速与埋深关系散点图(曲线)存在2个拐点，采用一元二次函数模型或幂函数模型来拟合该段曲线必然会产生较大偏差。

由表2 可知，采用一元四次函数模型在埋深区间[75，98]上的拟合参数计算获得的场地覆盖层厚度为91.55m，与实测平均值(91.6m)最为接近。若以场地覆盖层厚度计算值与实测平均值的差值不超过0.5m为限(因钻孔波速测试间距为1.0m，实测场地覆盖层厚度绝对误差绝对值≥0.5m)，则在埋深区间[0，98]上的一元四次函数模型以及在埋深区间[75，98]上的一元二次函数模型、 一元四次函数模型拟合结果可以满足计算场地覆盖层厚度的要求。

方安平等(2009)认为，对拟合结果做出正确解释是相当艰难的，通常情况下可以根据拟合的校正决定系数R2、 标准差SD(或加权卡方检验系数)以及残差分析而得出拟合结果的优劣。综上所述，笔者认为，在对拟合结果优劣的判别中，除了应考虑拟合曲线的R2值、SD值以及残差分析等指标因素外，还应考虑在统计区间上数学模型函数曲线几何图形与实测数据散点图图形的匹配性、 计算场地覆盖层厚度的精度要求以及回归公式的简便性等因素。针对计算场地覆盖层厚度的需要，长垣县主城区场地剪切波速与埋深关系推荐使用在埋深区间[75，98]上的一元二次函数模型及其拟合参数。

3 剪切波速平均值计算与应用

3.1 剪切波速平均值计算公式推导

根据高等数学中的积分中值定理(同济大学应用数学系，2002)，如果函数v(h)在闭区间[h1，h2]上连续，则在积分区间[h1，h2]上至少存在1个点ζ，使式(11)成立：

(11)

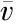
(12)

(13)

(14)

(15)

(16)

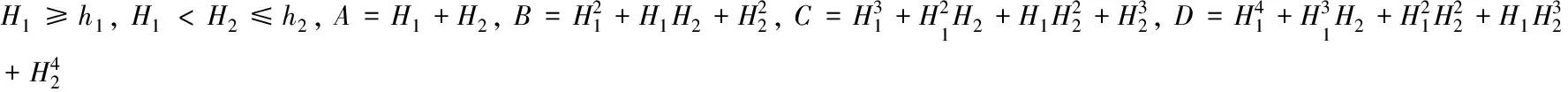
式(12)—(16)分别为基于土层剪切波速与埋深关系的线性函数模型、 一元二次函数模型、 幂函数模型、 一元三次函数模型、 一元四次函数模型推导出的土层剪切波速平均值计算公式。有趣的是，自式(12)、 (13)、 (15)至式(16)，具有一定的规律性，可类似地递推出基于一元更高次函数模型的函数平均值计算公式。

3.2 等效剪切波速计算公式推导与应用

作为1个实用特例，若土层等效剪切波速计算深度为d0(m)，即取H1为0.0m，H2为d0(m)，分别代入式(12)—(16)，可得基于土层剪切波速与埋深关系的线性函数模型、 一元二次函数模型、 幂函数模型、 一元三次函数模型、 一元四次函数模型的土层等效剪切波速vse(m/s)，计算公式分别为

(17)

(18)

(19)

(20)

(21)

依据现行建筑抗震设计规范(GB50011-2010)，计算深度d0取覆盖层厚度H值和20m两者中的较小值。显然，式(17)的几何意义是采用式(17)计算的等效剪切波速值为在埋深区间[0.0，d0]中点处(即h取0.5d0)的线性函数模型(式(1)的函数值)。

对于长垣县场地而言，计算深度d0取20m。将表1 中各个模型的拟合参数分别代入式(17)—(21)中，可得长垣县主城区场地土层等效剪切波速计算值(表3)。

表3 长垣县土层等效剪切波速计算结果

Table3 Calculation results of equivalent shear wave velocity of soil layer in Changyuan County

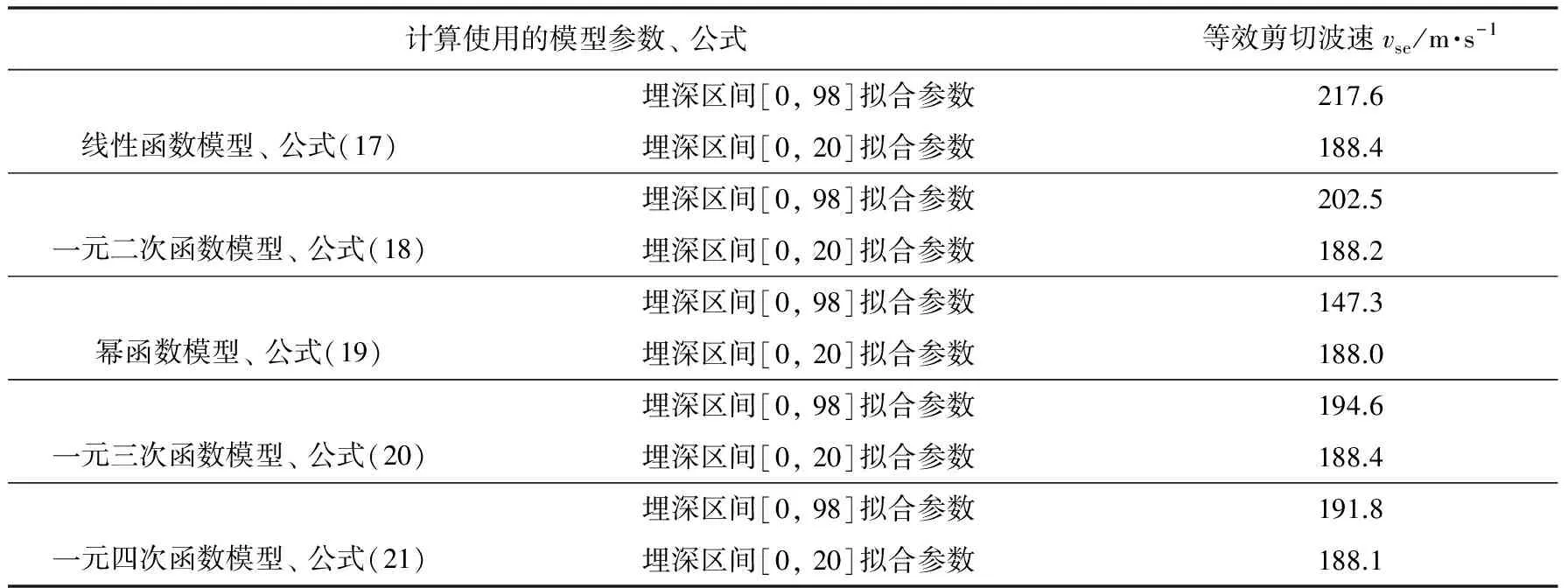
计算使用的模型参数、公式等效剪切波速vse/m·s-1线性函数模型、公式(17)埋深区间[0，98]拟合参数217．6埋深区间[0，20]拟合参数188．4一元二次函数模型、公式(18)埋深区间[0，98]拟合参数202．5埋深区间[0，20]拟合参数188．2幂函数模型、公式(19)埋深区间[0，98]拟合参数147．3埋深区间[0，20]拟合参数188．0一元三次函数模型、公式(20)埋深区间[0，98]拟合参数194．6埋深区间[0，20]拟合参数188．4一元四次函数模型、公式(21)埋深区间[0，98]拟合参数191．8埋深区间[0，20]拟合参数188．1

表3表明，利用埋深区间[0，98]上的各个数学模型及其拟合参数和相应公式计算获得的等效剪切波速计算值与实测平均值(184.2m/s)之间的差值较大，相差7.6～36.9m/s； 而在埋深区间[0，20]上计算获得的等效剪切波速计算值与实测平均值之间的差值较小，≤4.3m/s，即其相对误差 ≤2.3% 。从求取土层等效剪切波速的角度看，采用拟合曲线的标准差SD值来评价拟合效果的优劣比较符合实际，而采用校正决定系数R2值来评价拟合结果同样存在误判。

综上分析，考虑到土层等效剪切波速计算值的精度、 回归公式的简便性、 拟合曲线的R2值、SD值、 残差以及在统计区间上数学模型函数曲线几何图形与实测数据散点图图形的匹配性等因素，长垣县主城区剪切波速与埋深关系推荐使用在埋深区间[0，20]上的线性函数模型及其拟合参数。

3.3 时深转换求取反射波组埋深计算公式推导

在反射波地震勘探中，时深转换是指将地震反射时间剖面转换为地质剖面，即将反射时间转换为埋藏深度，其计算公式为(许强等，2009)

(22)

式(22)中，H0为地层反射波组埋深(m)； v0为反射波自地面至地层反射波组处的平均速度(m/s)，可由反射地震勘探资料分析计算给出或地层测井以及钻孔波速测试等资料给出； t0为反射波组的双程垂直到时(s)，由地震勘探野外原始地震记录经过一系列资料处理后得到的地震反射时间剖面图给出。

在横波(剪切波)浅层反射地震勘探中，若地层反射波组埋深H0位于当地剪切波速与埋深关系统计区间[H1，H2]内，则取H1为0.0m，H2为H0，分别代入式(12)—(16)，可得v0表达式，再将其代入式(22)，可分别获得地层反射波组埋深H0的计算公式或方程为

(23)

(24)

(25)

(26)

(27)

值得指出的是，式(24)，方程(26)、 (27)计算结果的判别应结合土层剪切波速与埋深关系统计的埋深区间。

目前，在隐伏(活)断层地震勘探中，P波地震勘探比横波地震勘探的应用更加广泛。如果在P波地震勘探区有钻孔P波测试数据，地层P波波速与埋深关系也满足上述统计数学模型，则上述公式也同样适用于P波反射法浅层地震勘探中的时深转换计算。

4 钻孔波速与埋深关系统计及应用方法步骤

为了充分挖掘钻孔波速测试资料信息，提高波速测试成果应用价值，在一个新的地区能够推广应用上述公式，提出下列钻孔波速与埋深关系统计及应用方法步骤：

(1)对新地区场地钻探与波速测试等相关资料进行分析研究，划分地震工程地质单元。在场地调查、 勘察和收集资料的基础上，对钻探与波速测试资料、 地貌资料、 地质构造资料、 工程地质与水文地质资料、 工程地震资料等一系列资料进行分析研究，将地貌单元类型相同、 地层地质年代和成因类型相同，场地地震工程地质条件与水文地质条件相同的区域划分为同一个地震工程地质单元。

(2)在同一个地震工程地质单元内，对钻孔波速测试数据进行统计分析，综合判别和选择土层波速与埋深统计关系的统计数学模型及其拟合参数。在统计分析时，首先，宜针对应用目的确定统计区间。例如，为了计算场地土层等效剪切波速，统计区间宜为地面至计算深度即[0，d0]； 为了计算场地覆盖层厚度，统计区间宜为场地覆盖层埋深上下一定范围； 为了计算地层反射波组埋深，统计区间可为地面至波速测试深度。当然，对波速-埋深散点图形状简单(无拐点)的情况，也可采用1个统计区间(地面至波速测试深度)进行统计； 而对散点图形状复杂(拐点多)的情况，也可采用多个统计区间即分多段进行统计。第二，选择与统计区间内波速-埋深散点图形状相匹配的统计数学模型。例如，散点图形状为 “线状”时可采用线性函数模型，散点图形状有1个拐点时可采用一元二次函数模型、 幂函数模型等，散点图形状有2个拐点时可采用一元三次函数模型、 一元四次函数模型等统计数学模型。第三，采用Origin等统计软件对实测波速数据进行统计，获得统计数学模型的相应回归公式及其拟合参数。最后，再结合校正决定系数R2、 标准差SD(或加权卡方检验系数)、 残差、 回归公式的简便性等因素进行综合判别，选择和确定统计数学模型及其拟合参数。

(3)根据上述统计分析选择的回归公式及其拟合参数，将拟合参数代入基于其统计数学模型及其拟合参数的场地覆盖层厚度计算公式、 土层等效剪切波速计算公式或地层反射波组埋深计算公式(方程)，即可获得场地覆盖层厚度、 等效剪切波速或地层反射波组埋深。例如，长垣县主城区场地剪切波速与埋深关系在埋深区间[75，98]上选择采用一元二次函数模型及其拟合参数，将表1 中其拟合参数代入式(7)，即可获得该场地覆盖层厚度为91.32m； 在埋深区间[0，20]上选择采用线性函数模型及其拟合参数，将表1 中其拟合参数代入式(17)，即可获得该场地土层等效剪切波速为188.4m/s。

5 结论与建议

(1)基于土层剪切波速与埋深关系的线性函数模型、 一元二次函数模型、 幂函数模型、 一元三次函数模型、 一元四次函数模型等统计数学模型，推导了统计埋深区间内任意埋深段土层剪切波速平均值计算公式、 土层等效剪切波速计算公式、 反射法浅层地震勘探中时深转换时反射波组埋深计算公式以及场地覆盖层厚度计算公式。这些新公式为提高土层剪切波速与埋深关系的回归公式的应用价值提供了有效途径。土层等效剪切波速计算公式、 场地覆盖层厚度计算公式等新公式在长垣县场地的应用效果良好。在钻孔波速测试中，如果土层P波波速与埋深关系也满足上述统计数学模型，则上述新公式同样适用于P波波速的相关计算和应用。

(2)土层剪切波速与埋深关系的统计数学模型的选择可采用试算法，统计区间也可采用分段区间。在对土层剪切波速与埋深关系拟合结果的优劣判别中，不但要考虑校正决定系数R2、 标准差SD、 残差等因素，而且要考虑在统计区间上数学模型函数曲线几何图形与实测数据散点图图形的匹配性、 回归公式的应用目的及其简便性，进行综合评判。针对计算长垣县场地覆盖层厚度、 土层等效剪切波速和反射波组埋深等应用目的，分别推荐采用在埋深区间[75，98]上的一元二次函数模型及其拟合参数、 在埋深区间[0，20]上的线性函数模型及其拟合参数和在埋深区间[0，98]上的一元四次函数模型及其拟合参数。

(3)在一个新地区的同一个地震工程地质单元内，利用较多钻孔剪切波速测试数据(分段)进行统计分析，可以建立该区土层剪切波速与埋深关系的(分段)统计数学模型及其拟合参数，将其拟合参数代入基于其统计数学模型的场地覆盖层厚度计算公式、 土层等效剪切波速计算公式或地层反射波组埋深计算公式(方程)，即可获得该区场地覆盖层厚度、 等效剪切波速或地层反射波组埋深； 并且计算获得的土层等效剪切波速值和场地覆盖层厚度值可以满足一般建设工程建筑的场地类别划分需要，亦可作为重要建设工程建筑的场地类别划分的参考依据。

曹振中，袁晓铭. 2010. 砂砾土液化的剪切波速判别方法 [J]. 岩石力学与工程学报，29(5): 943—952.

CAO Zhen-zhong，YUAN Xiao-ming. 2010. Shear wave velocity-based approach for evaluating gravel soils liquefaction [J]. Chinese Journal of Rock Mechanics and Engineering，29(5): 943—952(in Chinese).

陈国兴，徐建龙，袁灿勤. 1998. 南京城区岩土体剪切波速与土层深度的关系 [J]. 南京建筑工程学院学报，45(2)： 32—37.

CHEN Guo-xing，XU Jian-long，YUAN Can-qin. 1998. Relation between depth and shear wave velocity of soil and rock in Nanjing City [J]. Journal of Nanjing Architectural and Civil Engineering Institute，45(2)： 32—37(in Chinese).

范盛金. 1989. 一元三次方程的新求根公式与新判别法 [J]. 海南师范学院学报，2(2)： 91—98.

FAN Sheng-jin. 1989. A new extracting formula and a new distinguishing means on the one variable cubic equation [J]. Journal of Hainan Normal University: Natural Science，2(2)： 91—98(in Chinese).

方安平，叶卫平. 2009. Origin 8.0 实用指南 [M]. 北京： 机械工业出版社.

FANG An-ping，YE Wei-ping. 2009. Origin 8.0 Practical Guide [M]. China Machine Press，Beijing(in Chinese).

黄雅虹，吕悦军，兰景岩，等. 2010. 工程场地分类中等效剪切波速计算深度问题的讨论 [J]. 地震地质，32(2): 312—319. doi: 10.3969/j.issn.0253-4967.2010.02.014.

HUANG Ya-hong，LU Yue-jun，LAN Jing-yan，etal. 2010. Discussion on the issue of proper depth in calculating equivalent shear wave velocity for site classification [J]. Seismology and Geology，32(2): 312—319(in Chinese).

李小军. 2006. 工程场地地震安全性评价工作及相关技术问题 [J]. 震灾防御技术，1(1)： 15—24.

LI Xiao-jun. 2006. Evaluation of seismic safety for engineering sites and relevant technical problems [J]. Technology for Earthquake Disaster Prevention，1(1)： 15—24(in Chinese).

刘保金，赵成彬，尹功明，等. 2008. 浅层人工地震P波和S波资料揭示的郑州老鸦陈断层特征 [J]. 地震地质，30(2): 505—515.

LIU Bao-jin，ZHAO Cheng-bin，YIN Gong-ming，etal. 2008. The characteristics of the Laoyachen Fault in Zhengzhou revealed by shallow seismic data of P wave and S wave [J]. Seismology and Geology，30(2): 505—515(in Chinese).

刘红帅，郑桐，齐文浩，等. 2010. 常规土类剪切波速与埋深的关系分析 [J]. 岩土工程学报，32(7)： 1142—1149.

LIU Hong-shuai，ZHENG Tong，QI Wen-hao，etal. 2010. Relationship between shear wave velocity and depth of conventional soils [J]. Chinese Journal of Geotechnical Engineering，32(7)： 1142—1149(in Chinese).

彭艳菊，吕悦军，黄雅虹，等. 2009. 工程地震中的场地分类方法及适用性评述 [J]. 地震地质，31(2): 349—362. doi: 10.3969/j.issn.0253-4967.2009.02.016.

PENG Yan-ju，LÜ Yue-jun，HUANG Ya-hong，etal. 2009. A review on site classification method and its applicability in earthquake engineering [J]. Seismology and Geology，31(2): 349—362(in Chinese).

邱志刚，薄景山，罗奇峰. 2011. 土壤剪切波速与埋深关系的统计分析 [J]. 世界地震工程，27(3)： 81—88.

QIU Zhi-gang，BO Jing-shan，LUO Qi-feng. 201l. Statistical analysis of relationship between shear wave velocity and depth of soil [J]. World Earthquake Engineering，27(3)： 81—88(in Chinese).

同济大学应用数学系. 2002. 高等数学(上册)· 第五版[M]. 北京： 高等教育出版社. 232—233.

Department of Applied Mathematics of Tongji University. 2002. Advanced Mathematics，5th Edition(Volume I)[M]. China Higher Education Press，Beijing. 232—233(in Chinese).

许强，张学强. 2009. 横波地震在工程勘察中的应用 [J]. 工程地球物理学报，6(6)： 746—749.

XU Qiang，ZHANG Xue-qiang. 2009. The application of S-wave seismic to engineering investigation [J]. Chinese Journal of Engineering Geophysics，6(6)： 746—749(in Chinese).

袁晓铭，孙锐. 2011. 中国规范液化分析方法的发展设想 [J]. 岩土力学，32(增刊2): 351—358.

YUAN Xiao-ming，SUN Rui. 2011. Proposals of liquefaction analytical methods in Chinese seismic design provisions [J]. Rock and Soil Mechanics，32(Suppl 2): 351—358(in Chinese).

中华人民共和国住房与城乡建设部，国家质量监督检验检疫总局. 2010. 建筑抗震设计规范(GB 50011-2010)[S]. 北京: 中国建筑工业出版社. 19—20.

Ministry of Housing and Urban-Rural Development，General Administration of Quality Supervision，Inspection and Quarantine of People’s Republic of China. 2010. National Standards of People’s Republic of China GB 50011-2001: Code for Seismic Design of Buildings [S]. China Architecture & Building Press，Beijing. 19—20(in Chinese).

钟晓鸣，万小笠. 2009. Excel在统计分析中的应用 [M]. 北京： 科学出版社.

ZHONG Xiao-ming，WANG Xiao-li. 2009. Application of EXCEL in Statistical Analysis [M]. Science Press，Beijing(in Chinese).

APPLICATION AND STATISTICAL ANALYSIS OF RELATIONSHIP BETWEEN SHEAR WAVE VELOCITY AND DEPTH OF SOIL-LAYERS

HE Wei-min LIU Ming-jun YANG Jie

(GeophysicalExplorationCenter，ChinaEarthquakeAdministration，Zhengzhou450002，China)

The shear wave velocity is one of the important parameters in seismic engineering. The common mathematical models of relationship between shear wave velocity and depth of soil-layers are linear function model，quadratic function model，power function model，cubic function model，and quartic function model. It is generally believed that the regression formulae based on aforementioned mathematical models are mainly used for preliminary estimation of the local shear wave velocity. In order to increase the value of test data of wave speed in boreholes，the calculation formulae for the thickness of ground cover layer are derived based on the aforementioned mathematical models and their fitting parameters. The calculation formulae for the mean shear wave velocity of soil-layers are derived by integral mean value theorem. Accordingly，the calculation formulae for the equivalent shear wave velocity of soil-layers are derived. The calculation formulae for the depth of reflective waves in time-depth conversion of the reflection seismic exploration are derived. Through the statistical analysis of test data of shear wave velocity of soil layers in Changyuan County，Henan Province，regression formulae and their fitting parameters of aforementioned mathematical models are obtained. The results show that in the determination of the quality of these regression formulae and their fitting parameters，the adjusted R-square，root mean square error and residual error，the matching on the statistical range between the geometry of function of mathematical models used and the scattergram of the measured data，the application purpose and the simplicity of the regression formulae should be considered. With the aforementioned new formulae，the results show that the calculated values of equivalent shear wave velocity of soil-layers and thickness of ground cover layer meet the engineering needs. The steps for statistics and applications of the relationship between shear wave velocity and depth of soil-layers for a new area are as follows: (1)Analyze the relevant data about the site such as the drilling and wave speed test data，etc. and divide the site into seismic engineering geological units; (2)In a single seismic engineering geological unit，make statistical analysis of the data of borehole wave speed test，comprehensively identify and select mathematical models and their fitting parameters of the relationship between shear wave velocity and depth of soil-layers; (3)Substitute the selected fitting parameters into the formulae，based on their mathematical models for the thickness of ground cover layer，or the equivalent shear wave velocity of soil-layers，or the depth of reflective wave，then the thickness of ground covering layer，equivalent shear wave velocity，and depth of reflective wave are obtained.

equivalent shear wave velocity，the thickness of ground covering layer，time-depth conversion，earthquake engineering

10.3969/j.issn.0253- 4967.2016.04.011

2015-10-27收稿，2016-03-25改回。

中国地震局地震科技星火计划攻关项目(XH15058)资助。

P315.9

A

0253-4967(2016)04-0937-13

贺为民，男，1965年生，2008年毕业于中国地质大学(北京)地质工程专业，获博士学位，高级工程师，主要从事地震工程、 地震地质等方面的研究，电话： 0371-69133028，E-mail: wmhe65@163.com。