S变换对地震信号滤波的应用研究
徐涛
(武夷学院机电工程学院,福建武夷山354300)
S变换对地震信号滤波的应用研究
徐涛
(武夷学院机电工程学院,福建武夷山354300)
短时傅里叶变换的窗函数宽度固定不变,处理非平稳信号有局限性,改变窗函数使其可调,即为S变换。S变换的窗函数可以随信号自适应调节,信号经S变换得二维时频谱,确定噪声时频范围对其清零,再利用S逆变换到时间域,最终得到去噪后的有效信号。通过理论计算和地震信号仿真表明,S变换能够得到信号的时频信息,确定噪声的时间范围,并能有效滤除不同时段不同频率的噪声,提高信号的信噪比。
S变换;窗函数;地震信号
经典傅里叶变换是处理稳态信号的有效方法,可以立即得出信号的频谱信息,但无法反映出信号频率随时间的变化情况,基于此,提出了窗函数的概念,使时域信号在此窗内能够体现频率信息,这种处理方法称为时频分析方法[1],其中,CWT、STFT是比较有代表性的时频分析方法。但时频分析法的局限性在于无法有效处理变化剧烈的非平稳信号,且时频分析方法的窗函数仍受到Heisenberg W不确定性原理的限制,即时频分辨率无法共同达到最优。
地球物理学家Stockwell R G在1996年提出了一种加时窗的时频可逆分析方法,也就是S变换[2]。S变换是在STFT基础上对窗函数进行改进[3-4],采用CWT思想,以Morlet小波(具有非正交性和Gaussian调节的指数赋值小波)为基本小波,根据不同时间区域信号的剧烈程度,确定合适的时窗分辨率,从而计算出不同时刻的功率谱,确定噪声存在的区域,对该区域进行清零,再经S逆变换到时间域,最终得到滤波后的有效信息。与STFT、CWT相比,S变换有其独特的优势[5-6]:窗函数分辨率具有多分辨性,宽度又可以随信号频率自适应地做出改变,其Morlet小波可以不受容许性条件限制等[7]。
1 S变换
1.1 由傅里叶变换导出
设为连续时间序列,其傅里叶变换表达式可以表示为:H(f)=由于傅里叶变换无法分析非平稳信号的局部信息,也无法体现信号频率随时间的变化情况,针对这些缺陷,在1946年,Gabor率先提出了加窗函数的思想,即在h(t)上乘以一个窗函数,设为w(t),用w(t)按时间轴去截每段信号,再对截下来的每段信号作傅里叶变换,所得到的一系列傅里叶变换结果排开则成为二维表象,这些傅里叶变换的集合记为:H(f)=(2),可以证明,窗函数的时频宽度的乘积存在最小值,其最小值为2,这恰恰符合了测不确定性原理,该原理说明了不可能同时获得最佳的时频分辨率。基于此,将窗函数归一化,定义为高斯窗,且该高斯窗可以平移和伸缩,平移量为τ、伸缩量为σ,那么,w(t-τ)=此时时间序列h(t)的时间频率二维表象又可写为:

(4),上式除了时间和频率二维表象元素外,还多了一个伸缩变量σ,作为时频分析工具是不切实际的。考虑将伸缩变量与频率产生关系,令,这样就得到一个公式:S(t,f)=exp(-j2πft)dt(5),这就是连续时间序列h(t)的S变换表达式。根据傅里叶逆变换很容易得到:该式为S逆变换表达式。
1.2 离散S变换及其实现
由于计算机处理的是离散信号,而在离散域内,又必须满足周期性或有限性条件,所以必须要导出有限序列的离散S变换。
h(KT),K=0,1,2,…,N为连续信号h(t)的离散信息,T为采样时间间隔,其离散傅里叶变换可以表示为:N,时间序列h(KT)的离散S变换可以表示为:(8),式中N为采样点数,j为正整数且无单位,m和n为频率,是h的离散傅里叶变换。离散S反变换为:中,n≠0。
1.3 S变换的实现
首先记n=n/NT,m=m/NT,k=kT和j=jT。序列h(k)的S正变换步骤如下:
(1)在时间序列h(k)上进行采样,设采样点数为N,采样时间间隔为T,对这N个点求FFT(快速傅里叶变换),得到其频谱,记为H[m]。
(2)计算频率为n的高斯函数值G[m,n]。
(3)将H[m]向左移动n个频率单位得H[m+n],即频移谱。
(4)将G[m,n]乘以H[m+n]所得结果记作B[n,m]。
(5)将B[n,m]做快速傅里叶逆变换,得其S变换谱表达式S[n,j],j=1,2,…,N。
(6)返回执行步骤(3)、(4),当所有频率全部计算完毕,就得到了h(K)的S变换谱。
同样,可以根据S逆变换的离散形式得出S逆变换步骤:
(1)对谱S[n,j]按行求和,计算出频率n的傅里叶谱,记为C[n]。
(2)循环频率n,返回再执行步骤(1),计算出谱H[m]。
(3)对H[m]执行傅里叶逆变换运算,还原得出时间序列h(k)。
2 S变换在时频域上的滤波
2.1 滤波方法简介
短时傅里叶变换在对信号进行滤波时,是比较常用的方法,对比傅里叶变换最大的优点就是,添加了可伸缩可平移的高斯窗函数,能够获取信号在各个时刻对应的频谱信息,但是高斯窗函数不够灵活,缺乏自适应性,因此无法跟踪信号的突变过程,而信号的噪声部分又往往发生在该过程,即信号突变区,所以设置随信号频率变化的自适应高斯窗函数显得尤为重要,用自适应的高斯窗函数对信号进行截取,得到不同时间对应的频域信息,在时间-频率这个二维平面上就确定了信号噪声的存在的时间频率范围,简单来说就是将信号分为有效部分和噪声部分,利用S变换,得到信号的时频谱,确定噪声区域,将噪声区域清零,然后经逆S变换回时间域,具体做法如下,将信号表示为originalsignal(t)=realsignal(t)+noise(t),等式右边为原始信号,左边为有效信号和噪声信号,将两边进行S变换得:SToriginalsignal(t)=STrealsignal(t)+STnoise(t)。在信号S谱上确定噪声区域,对该区域清零,也就是让STnoise(t)为0,最后将STrealsignal(t)经S逆变换回时间域,最终得到清除干扰后的近似有效信号realsignal(t)。
2.2 滤波步骤
(1)首先对待处理信号进行S变换,得其S谱,即时间-频率信息,如图1。

图1 信号S变换时频图Figure 1 Time frequency diagram of signal’s S-transform
(2)确定噪声区域,即时间范围[t1,t2]和频率范围[f1,f2],将此二维时间-频率区域标为D,注意,有效信息和噪声信息的边界是一个敏感区域(误差产生区域),边界可以通过对信号分时分频计算来确定。
(3)对噪声区域进行清零。
(4)对清零后数据进行S逆变换,最终得到滤除噪声后的时间域信息。
3 S变换与小波变换模型试算
图2是一幅原始的待处理的信号,由人工叠加噪声合成,为时间域信息;图3为该信号经S变换后的时频谱,得到由低到高的三段频率信息,分别为0.05、0.1和0.15 Hz,其中,0.05 Hz的低频信号上叠加了高斯白噪声,噪声功率约为0.6,此时的信噪比为7.923 5;原始信号的S变换谱中可以清楚的看到三段不同频率的信号以及它们存在的时间区域,同时也能够清楚的看到噪声所在的时频区域(频率区域大概为0.2~ 0.6 Hz,时间区域大概为65~85 s),对这部分区域进行清零,将噪声清除,然后将S变换后的时频谱反变换回时间域,得到去噪后的近似有效信号,如图4,可以看出通过S变换后滤波并不是完全彻底,这是由于在对噪声时频范围的确定时存在误差信息,滤波后信号除开始部分、与噪声产生的频率段产生些许畸变外,其余部分与原信号基本一致,经计算,滤波后信号信噪比约为12.355 6,大大提高了信噪比。图5为信号经过小波变换滤波后的结果,经过计算,经小波变换滤波后的信号信噪比为11.423 3,对比得出,S变换滤波效果要优于小波变换滤波结果。
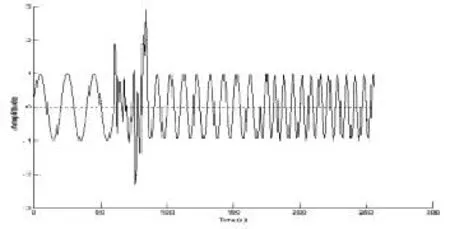
图2 人工合成噪声的原始信号Figure 2 Artificial synthetic raw noise signal

图3 原始信号经S变换后的时频谱Figure 3 Time spectrum after S-transform
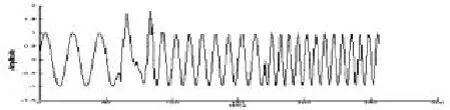
图4 经S变换滤波后的时域信息Figure 4 Time domain signal after S-transform filtering

图5 经小波变换滤波后的时域信息Figure 5 Time domain signal after wavelet transform filtering
4 S变换对实际地震信号去噪
图5为某一地区的实际地震记录资料,选取60道地震信号进行滤波分析,其中每一道的道长为3 s,信息的采样点数为1 500,采样间隔为2 ms,从图中可以看出每一道信号在低频的基础上叠加了高频信息,分别取出每一道的地震信号,进行S变换,确定噪声存在时频区域,对噪声进行清零,然后返回时间域,直到处理完所有的60道信号,最终得到去噪后的60道地震时域信息如图6。

图6 原始地震信号Figure 6 Original seismic signal

图7 去噪后的地震信号Figure 7 Seismic signal after denoising
与图5比较可以明显看出这60道信号的高频部分干扰已经基本完全滤除,信号相对平稳与清晰。将60道信号的干扰信息完全滤除后,从宏观角度来看,这60道信息的干扰分量已经基本完全滤除,地震信息呈现低频状态且比较平稳,由此来看,基于S变换的去噪方法能够很好地对实际地震信息进行滤波。
5 结论
对比短时傅里叶变换S变换的优势在于,其窗函数可以根据信号特征调整其高度和宽度;对比小波变换其优势在于,信号的S变换结果更加直观,能够更加细致地对高频区进行分析。通过模型试算对比,S变换滤波方法要优于小波变换滤波方法。虽然S变换的窗函数可调,但是其形态还是保持不变,仅限于平移与伸缩,这样也就制约了S变换对信号分析的灵活度,另外,窗函数时频分辨率依然受测不确定性原理的约束。所以,基于S变换去噪方法仍有待于完善。
[1]焦叙明.时频分析及其在地震资料处理分析中的应用[D].青岛:中国海洋大学,2007.
[2]Stockwell R G,Mansinha L,Lowe R P.Location of the complex spectrum:the stransform[J].IEEE Transactions on Signal 1996;44(4):998-1001.
[3]杨志强,单娜林,刘占兴,等.S变换在岩溶区地震映像资料处理中的应用[J].工程地球物理学报,2012(2):227-230.
[4]迟华山,王红星,赵培红,等.基于S变换的线性调频信号时频滤波[J].无线电通信技术,2012(1):21-24.
[5]赵淑红,王璇.S变换时频滤波与其它滤波方法的比较[J].地震工程学报,2007(3):224-229.
[6]刘霞,徐涛,段玉波,等.基于广义S变换的时频滤波技术研究[J].自动化技术与应用,2012(2):15-19.
[7]Pinnegar C R,Mansinha L.Time-local spectral analysis for non-stationary time series:the S-transform for noisy signals [J].Fluctuation and Noise Letters,2003,3(3):357-364.
(责任编辑:叶丽娜)
Application Study on S-transform to Seismic Signal Filteration
XU Tao
(School of Mechanical and Electrical Engineering,Wuyi University,Wuyishan,Fujian 354300)
The width of the short time Fourier transform window function is invariable.There are limitations in dealing with non-stationary signals.Change window function and make it adjustable,this is S-transform.The window function of S-transform can be adjusted with signals.The signal is transformed to be two dimensional time-frequency spectrum by S-transform.Determine the time-frequency range of noise and clear the noise.it is transformed to be time domain by S-inverse-transform.Finally,obtain the effective and filtered information. Through the theoretical calculation and simulation of seismic signal,S-transform can get the time frequency information of signal,determine time scope of the noise,improve the SNR of signal.
S transform;window function;seismic signal
TN911.72
A
1674-2109(2016)12-0059-04
2015-09-12
徐涛(1984-)男,汉族,助教,主要从事故障诊断与容错控制的研究。

