面向多级中断系统的任务最差响应时间分析
于广良,杨孟飞,徐建,姜宏
1.北京控制工程研究所,北京100190 2.中国空间技术研究院,北京100094
面向多级中断系统的任务最差响应时间分析
于广良1,*,杨孟飞2,徐建1,姜宏1
1.北京控制工程研究所,北京100190 2.中国空间技术研究院,北京100094
针对航天嵌入式系统中存在多级中断情况下的时间分析问题,提出了中断与任务混合的响应时间计算模型。该模型中断与任务使用统一的优先级定义,将多级中断嵌套的响应时间分析与任务嵌套的响应时间分析相结合,推导出了混合模型下响应时间计算公式。并进一步比较了中断与任务的异同,阐述了公式中关键参数的含义与计算方法。最后利用开源的LEON3平台和Modelsim软件对所述方法进行了仿真验证,结果表明,任务最差响应时间过估小于5%,可以得到准确的分析结果,有较高的工程应用价值。
实时系统;嵌入式软件;多级中断;固定优先级调度;可调度性分析;最差响应时间;航天器
对于航天嵌入式系统而言,其上运行的软件通常有着明确的时间约束,保证其正确性的一个关键问题是保证各个任务在其截止时间之前完成。由于此类系统通常使用中断方式接收和处理来自外部设备的各种随机或周期信号,随时随处都会发生的中断成为影响实时性的一个重要因素,当系统中有多级中断时更是如此[1]。
中断会打断任务程序的执行,引入额外的时间开销,这对于验证任务是否满足其截止时间提出了挑战。最差响应时间(Worst Case Response Time,WCRT)[2]是指任务从释放到执行完成的最大可能时间间隔,通常的分析是针对任务间的抢占情况,通过计算各任务被其他任务抢占时的最差响应时间,将其与该任务的截止时间比较,以求得出任务集的可调度性,目前这方面研究已有进展[3-4]。但是对于中断影响下的任务时间特性的分析研究还比较少。
文献[5]考虑了中断驱动程序截止时间分析问题,即检查每个中断是否都能在截止时间前处理完成。文献[6]利用了上下文切换次数限制和采用基本路径来限制需搜索的路径空间,将中断驱动程序转化为顺序程序进行分析,以得出主程序在多个中断服务程序(Interrupt Service Routine,ISR)影响下的最差执行时间。文献[7]分析了卫星控制系统时序问题,建立了包含中断在内的时序模型。文献[8]考虑了中断处理开销对动态优先级系统可调度性的影响,文献[9]则考虑了多处理器系统的中断开销计算。
但是上述研究都将中断单独考虑,没有与任务的时间分析方法融合。本文将中断集与任务集结合起来,定义统一的参数并在一个统一的优先级空间里进行分析。利用任务响应时间分析方法来分析多级中断下的任务最差响应时间,仿真结果表明本文所述方法可以很好地推广到包含多级中断系统的时间和时序分析中。
1 系统描述及模型定义
1.1 系统描述
本文研究的航天嵌入式系统软件模型由任务程序和中断服务程序组成,如图1所示。系统在上电复位之后首先进行硬件的初始化,在最开始部分是初始化中断向量表,为每个中断的服务程序定义一个入口地址;完成硬件初始化后跳转到系统主函数,完成系统的配置及操作系统内核初始化等;最后使能中断,内核启动空闲任务,等待各个满足条件的任务进行调度(如图1中任务1到任务N所示)。在任务运行期间,如果有中断请求信号产生,则处理器会响应相应的中断请求,运行图1中中断1到中断M代表的中断服务程序。
一般来说,处理器的异常包含了中断、陷阱、故障和终止。陷阱、故障和终止通常是同步发生的,是执行当前指令的结果,中断是异步发生的,是来自处理器外部的I/O设备的信号的结果[10]。本文只考虑异步中断,不考虑其他异常控制流。
中断对低优先级任务的抢占除了引入其最差执行时间之外,其中一项非常重要的代价是由于高速缓存(cache)块的驱逐引起的。中断可能会将对低优先级任务有用高速缓存块驱逐出高速缓存,导致重新运行低优先级任务时这些高速缓存块需要从内存中重新加载,这段抢占代价称为高速缓存相关的抢占延迟(Cache Related Preemption Delay,CRPD),其大小限界为g×tbr,其中g为由于抢占导致的重新加载的高速缓存块数目的上限,tbr为从内存中加载块到高速缓存内需要的时间上限[11]。本文研究的是航天嵌入式系统,通常为了保证时间确定性,较少使用高速缓存,本文为了简化分析,暂不考 虑cache的影响,对其分析将作为以后的工作。
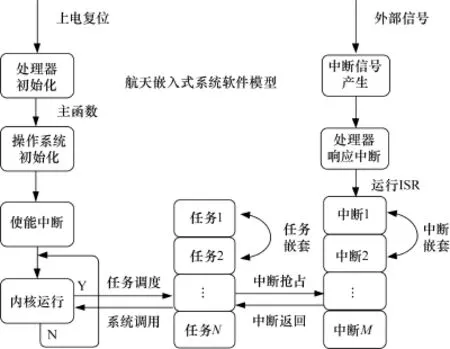
图1 航天嵌入式系统软件模型Fig.1 Software model of aerospace embedded system
1.2 模型定义
本文考虑的系统采用固定优先级抢占式调度,允许多级中断嵌套。系统的中断服务程序集定义为IM=(ξ1,ξ2,…,ξm),任务集定义为TN=(τ1,τ2,…,τn),对中断和任务而言,下标顺序代表了其优先级顺序,下标越小,则优先级越高,任务和中断都具有惟一独有的优先级。为了方便起见,本文使用相同的符号表示任务和中断,将中断与任务的混合集定义为(τ1,τ2,…,τm,τm+1,…,τm+n),按照优先级从大到小排列,下标从1到m代表中断,从m+1到n代表任务。在需要区分时,用下标τ和ξ来分别代表任务和中断的性质。所用到的符号及其描述(i=1,2,…,m+n):τi为任务集中优先级为i的任务;ξi为中断集中优先级为i的中断;ri为任务的释放时间或者中断的触发时间;ai为任务的到达时间或中断信号的产生时间;si为任务或者中断的开始执行时间;fi为任务或者中断的执行完成时间;Ci为任务或者中断的最差执行时间;Di为任务或者中断的相对时间限(相对于任务到达时间或者中断产生时间);Ti为任务或者中断的周期,对于非周期任务和中断为其最小间隔时间;Bi为任务的阻塞时间,或者中断禁止导致的中断延迟时间;Ji为任务或者中断的释放抖动时间,即为任务从到达到释放或者中断从信号产生到触发的时间;Ri为任务或者中断的响应时间,有Ri= fi-ri。
定义hp(i)和lp(i)代表优先级高于和低于τi或ξi任务和中断,用hep(i)和lep(i)代表优先级大于等于或者小于等于τi或ξi的任务和中断。这里认为任务和中断的截止时间是受限的,即Di≤Ti。并且任务和中断一旦开始执行,不会停顿一直到执行完毕,除非被抢占或阻塞。任务的最差响应时间为其释放到其运行结束的最长时间,中断的最差响应时间为其被处理器识别到其运行完毕的最长时间。任务和中断的最差响应时间应该满足小于或等于截止时间减去其抖动时间Ri≤Di-Ji。
图2给出了上述模型的一个例子,整个系统由两个中断和两个任务组成,分别属于中断集和任务集,依照其优先级从高到低,统一进行编号,不过相同的参数对于中断与任务来说,含义可能不同。在任务2执行过程中任务1到达,然后被操作系统释放到就绪队列,调度器检测到高优先级任务1就绪则发起上下文切换,任务1抢占任务2得到优先运行,期间中断2被触发,系统响应中断后执行中断服务程序,中断2的中断服务程序运行期间中断1产生,发生中断嵌套,各自运行完成后依次返回,最后返回到任务2继续执行。

图2 任务与中断混合模型示例Fig.2 Example of task and ISR integrated model
2 响应时间分析
由图1和图2的系统模型和示例可以看出,系统中可能包含有任务嵌套、中断嵌套以及中断对任务的抢占。假设系统中没有或禁止中断,则某任务的响应时间主要受到高优先级任务抢占的影响,这是目前大部分响应时间分析所研究的问题。如果系统中存在中断,由于所有中断的优先级均高于任务的优先级,故某中断的响应时间主要受到高优先级中断抢占的影响,本节将详细阐述如何利用任务抢占下的任务响应时间分析方法来分析中断抢占下的中断响应时间。有了中断的响应时间分析,则容易分析系统中只有一个主函数,其他功能都是通过中断来实现的中断驱动程序的响应时间,此类系统的时间开销主要来自于中断的抢占。如果系统中同时存在任务嵌套与中断嵌套,这时候某任务的响应时间将分别受到高优先级任务抢占与中断抢占所带来的影响,利用前面所得到的分析结果也容易扩展到这种情况。
本节首先回顾固定优先级抢占式调度下任务的响应时间计算公式,接着说明如何利用其计算中断响应时间,进而得出中断驱动程序的响应时间计算,最后导出在多任务和多级中断情况下的任务的最差响应时间计算公式。
2.1 任务嵌套下的任务响应时间
对固定优先级抢占式调度的响应时间分析[]:
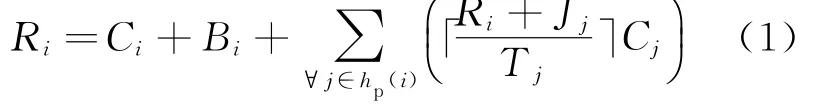
式中 ⌈·⌉为向上取整运算,代表任务τi的响应期间被任务τj抢占的最大次数;Ci为任务τi的最差执行时间;Bi为其最大阻塞时间;Jj为高优先级任务τj的释放抖动;Cj为其最差执行时间,Tj为其周期。
2.2 中断嵌套下的中断响应时间
利用式(1)计算中断嵌套下的中断响应时间,不改变公式的形式,式(1)中的参数含义采用第2.2节模型中的中断参数的定义,记为

对于式(2)的求解应从高优先级到低优先级依次进行,首先从最高优先级中断ξ1开始,由于其为最高优先级,所以hp(1)=Ø,根据式(2),其最差响应时间应为R1=C1+B1,其中C1为其最差执行时间,其值包含了从处理器跳转到返回之间的所有执行时间的最大值;B1为优先级小于1的中断程序和任务程序中的最长关中断的时间。
接着依次求解ξ2一直到ξm,对于ξm,其可能被ξm-1到ξ1抢占,所以hp(m)={ξm-1,ξm-2,…,ξ1},求解过程是一个迭代的过程。首先计算其不被中断情况下的最差响应时间为R0m= Cm+Bm,其中Cm为其最差执行时间,Bm为任务程序中最长关中断时间。考虑被抢占的情况,则有:

式(3)中上标n代表迭代次数,对于存在抢占情况下ξm响应时间的求取是一个迭代过程,迭代从R0m开始,直到Rnm=Rn-1m或者Rnm>Dm-Jm为止,前者表明已经求得最差响应时间为Rnm,而后者代表最差响应时间已经超过了ξm的截止时间限。需要说明的是,式(3)的迭代在优先级高于m的所有中断的总CPU利用率小于1时总会收敛,即总会有时间留给中断m执行,则最终会执行完毕。
下面做进一步说明,式(3)中⌈·⌉为ξm可能被高优先级中断抢占的最大次数,向上取整;包含了阻塞时间Bm,这是因为假设当系统关中断时产生中断,在系统开中断后将依次响应相应的中断请求,而不会丢失中断;使用Cj而不是Rj,是因为对于阻塞时间来说,如果中断j<m被阻塞,则可能存在两种情况:①中断m正在执行关中断区域,这段时间包含在了Cm中;②中断m也被阻塞,这段时间包含在了Bm中。对于中断j再被更高优先级的中断抢占的情况来说(中断m被更高优先级的中断间接抢占),也已经包含在抢占次数的计算里了。
对于中断而言,一般情况下,截止时间应小于其周期,这样便不会发生中断丢失。实际上,若在某中断响应期间,同一中断信号再次到来,只要这时已经清除了CPU的中断请求位,中断也不会丢失。但是这样的设计余量非常小,本文并不考虑这种极端情况,而认为中断的截止时间小于等于其周期,即Di≤Ti, 1≤i≤m。
2.3 中断嵌套下的任务响应时间
对于任务之间不存在嵌套,但是中断之间存在嵌套的中断驱动软件而言,某任务τi的响应时间为

式中Ci为任务τi的最差执行时间,由于任务间无嵌套,故不会被阻塞,因此没有包含阻塞时间。式(4)等式右端第2部分为所有中断对其可能的抢占所占用的时间。
2.4 中断与任务嵌套下的任务响应时间
由本节前面的分析可得,在图1和图2所示的集成模型里,某任务τi的响应时间为

其中,等式右边第3部分为优先级大于i的任务对其的抢占所占用的时间,第4部分为所有中断对其抢占所占用的时间。式(5)求解迭代到其响应时间不再变化或者超过截止时间为止,得到在中断与任务嵌套下的某任务的最差响应时间。
3 参数含义与计算方法
3.1 最差执行时间
程序的最差执行时间(Worst Case Execution Time,WCET)[12]是指在所有可能的情况中,程序在对应的硬件平台上执行时花费的最长时间。WCET给出了某段程序执行的时间上限,评判其分析方法或者工具好坏的两个准则是安全性和精确性:如果分析得到的时间大于程序的实际WCET值,称这种分析结果是“安全(Safe)”的;分析结果越接近实际的WCET值,称其越“精确(Precision)”。
WCET是任务自身(例如独享处理器)的最差行为,而WCRT是任务在任务集(例如共享同一处理器)中的最差行为,WCET分析是WCRT分析的基础。在一个实时系统中,当没有抢占时,可以用WCET来检查任务是否满足截止时间;当有多个任务允许抢占时,需要使用WCRT来验证是否满足时间约束。
寻找程序的WCET有静态分析和基于测量的方法共两种主流方法,代表性的商业工具有aiT和RapiTime等,在这里并不展开阐述,对于任务的最差执行时间可以通过上面任意一种方法或工具获得。但是对于中断的最差执行时间的获取却并不那么直接,因为其中包含了中断的切换时间。一个典型的中断处理流程如图3所示。
任务程序在t0时刻开始执行,t1时刻中断信号产生,t2时刻处理器开始响应中断,此时处理器将继续完成正在执行的指令(有些处理器可能允许中断长指令),完成断点保存并跳转到中断向量表处,以上部分由处理器自动完成。从t3时刻起执行中断向量表中指令并分支到相应的中断服务程序,开始任务上下文的保存等,从t4时刻到t5时刻为用户编写的中断服务程序的执行时间,到t6时刻恢复了被中断任务的上下文,中断服务程序处理完成,任务程序继续执行到t7时刻结束。
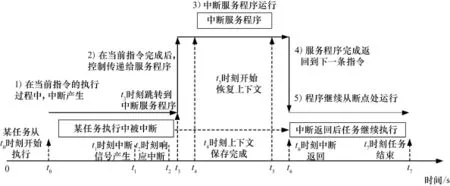
图3 中断服务时间流程Fig.3 Timeline of ISR
前述公式中中断的Cj(1≤j≤m)指的是t2~t6时间段,其中t2~t3时间段为CPU相关,设其最大时间为tξp;t3~t4时间段和t5~t6时间段为操作系统相关,分别设为tξo1和tξo2,总的为tξo;t4~t5时间段为用户相关,最大时间设为tξu。在分析的时候,应根据相应CPU手册和操作系统的说明并进行测试得到tξp和tξo,这两个时间是相对固定的。但对tξu而言,与应用相关,差别较大,这里对不同中断使用其优先级来区分,表示为tu,j,可得Cj= tξp+tξo+tu,j(1≤j≤m),与中断相比,任务抢占导致的上下文切换完全是由操作系统来完成的,故没有处理器跳转的时间,一般来说其切换效率要比中断低,花费的时间也比中断长。
3.2 最大阻塞时间
对任务而言,当其访问一些共享变量时,通常要确保独占性访问,此任务操作共享变量的指令构成了一个临界区,为了保证正确性,不同的任务执行临界区指令时,必须实现互斥的访问。一个低优先级任务通过锁定临界区来确保独占性访问时可以阻塞高优先级的任务,这样可能导致优先级反转的产生,采用优先级继承协议能够避免优先级反转问题,但是难以避免死锁的发生,采用优先级上限协议可以避免优先级反转和死锁[13]。
但是对于中断而言,为了保证快速响应,一般不能被阻塞,所以中断服务程序与任务间共享数据只能通过开关中断进行保护;同时任务程序中和中断服务程序中某些需要连续执行的部分也会采用关中断的方式进行保护。定义βi为任务程序和优先级小于ξi的中断服务程序中所有关中断区域的集合,设bmaxi为集合βi中关中断区域最差执行时间的最大值,则有Bi=bmaxi。
3.3 最小到达时间
对于周期性中断而言,其最小到达时间就是其周期。但对于随机中断,可能会随时到达,但通常会有一个最小的时间间隔。以总线的接收中断为例,其最小时间间隔为发送的数据包在线上的传输时间加上数据包发送之间的时间间隔[7]。
假设单次中断所需要的数据总传输位数为d,数据传输的速率为f,则可知其线上传输时间为设定两次数据之间的最小发送时间间隔为tδ,则可估算中断的最小触发周期为Tj= tδ,j+tl,j。
3.4 释放抖动
任务到达后不一定会被立刻被放到就绪队列里,这样从任务到达到其释放(放到就绪队列)之间的时间称为释放抖动。对中断而言,从中断信号产生到被识别(例如高电平触发,电平变高需维持一段时间被识别)的时间定义为中断的释放抖动,这段时间一般非常短暂。事实上,释放抖动使得中断连续两次触发的时间间隔并不严格等同于其周期,对于中断的多次释放,抖动对被抢占的任务或中断响应时间影响仅存在第一个和最后一个,设释放抖动的最大时间为tmaxJ,最小时间为tminJ,容易得到Jj=tmaxJ-tminJ。
4 仿真分析
以一个航天嵌入式控制软件为例分析,控制系统的任务通常是同步的、周期性的、由时间触发的。本文设定在一个任务周期内任务在各自分配的时间片内运行,没有相互间的嵌套和跨时间片任务,时间片的结束时刻是其截止时间。在不同的任务周期间,任务重复的运行。中断是异步发生的,它们可以抢占任务得到优先运行,造成任务执行时间的延迟,当系统中有多个中断时,中断之间还可能产生嵌套,这样不但要分析中断下任务的最差响应时间,同时需要分析中断嵌套下中断的最差响应时间。
4.1 环境配置
利用开源的处理器LEON3和自主开发的SpaceOS操作系统在Modelsim软件中仿真验证多级中断对任务响应时间的影响。LEON3是欧洲航天局下的Gaisler研究所开发的一个使用SPARC V8指令集的32位RISC处理器,它的源代码由可综合的VHDL代码构成。基于GPL许可证协议,LEON3非容错版本软核IP提供VHDL源代码。空间嵌入式操作系统SpaceOS是由北京控制工程研究所研制的星载计算机嵌入式操作系统,已经在多个航天型号任务上得到了应用[14]。
硬件环境配置是时钟频率为100 MHz,处理器核心数为1,寄存器窗口数目设置为8个,为保证时间确定性,不使用浮点数单元,整数单元不使用分支预测,不使用指令与数据cache,不开启存储器管理单元(MMU)。片外连接8 M×32bit的SRAM存储器,带有5个片内定时器和两个通用串口等。软件环境配置为使用分时调度,任务周期中断由外部中断0产生,时间片中断由定时器1产生,任务的读写等待周期全部设置为1。系统另外设计为包含4个任务和4个中断,相应参数如表1和表2所示,表1中TIMR1括号内的值是带有任务释放时的最差执行时间。

表1 系统的中断组成Table 1 Interrupts of the system

表2 系统的任务组成Table 2 Tasks of the system
表1和表2中WCET的值是通过测试的方法,采用大量仿真选取的最大值,由于系统的软硬件设计比较确定,所以时间波动很小,时间抖动则是采用第3.4节所述方法求得。对于最大阻塞时间Bi的计算,由于任务在不同的时间释放并在不同的时间区间内运行,所以任务间无阻塞发生。对中断而言,阻塞主要由关中断引起的,通过大量仿真得到,任务程序最长关中断时间为bmax=47.9μs,中断程序的最长关中断时间bmax=5.5μs,故Bi可以通过4.2节所述方法求得。
4.2 仿真结果分析
综上所述,计算得到的任务和中断最差响应时间与仿真得到的最差响应时间对比见表3。对于中断只给出了具有代表性的EXINT 0和 UART1的值,由于TIMER1和EXINT0不会同时发生,故表中UART(1)指的是在EXINT0抢占下的最差响应时间,UART(2)则是在TIMER1抢占下的最差响应时间。可以看出,所有任务的最差响应时间的分析值均大于仿真值,说明分析结果是安全的;同时最差响应时间的最大过估比率仅为3.74%,说明本文所述的多级中断下任务最差响应时间的计算方法是精确的。中断的最差响应时间最大过估比率达到31.09%,这是由于中断发生的随机性,很难使用测试的方法得到最差情况。当然一般情况下,中断并不会如此频繁发生,所以在实际的工程应用中对于中断的时间分析还需要设定一些约束条件,以便得到更加实用的结果,这将留作以后的工作。
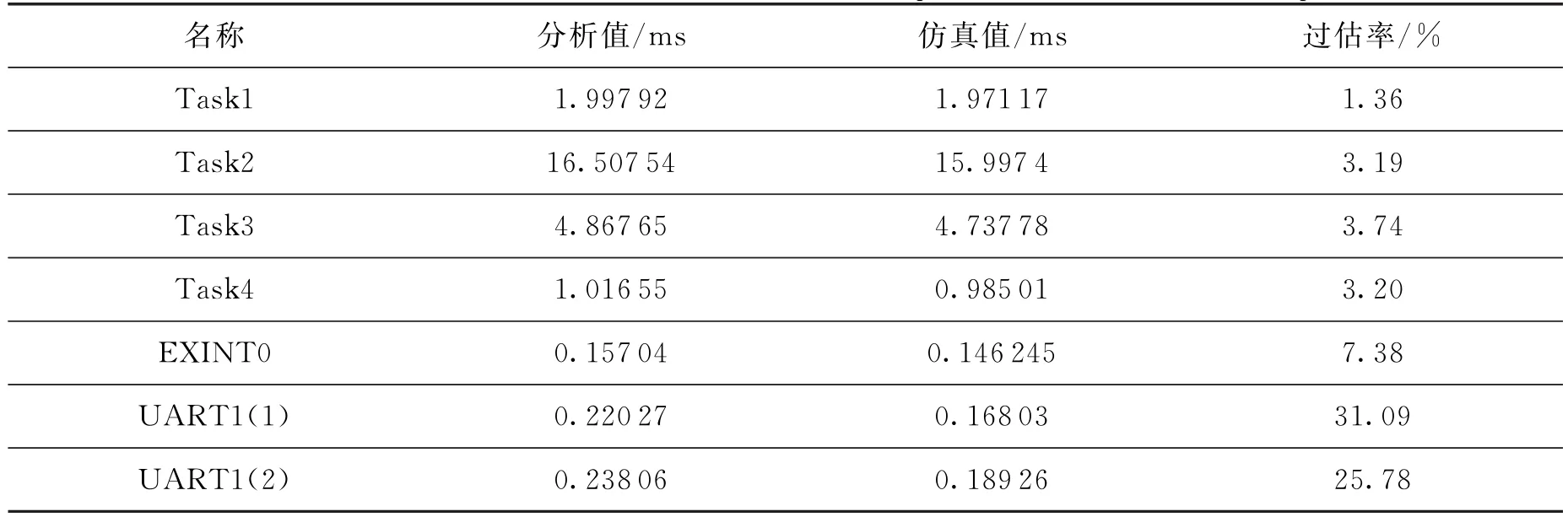
表3 多级中断下任务和中断最差响应时间结果Table 3 Results of WCRT of tasks and interrupts under multilevel interrupts
5 结束语
本文针对包含多级中断的航天嵌入式系统,通过定义中断与任务的混合时间分析模型,将任务间抢占的响应时间分析方法推广到了中断与任务混合抢占的时间分析中,更加符合航天嵌入式系统的应用环境。文中给出的仿真实例说明了该方法的有效性,但是在最差响应时间计算时,考虑的是最差情况而忽略了一些实际工程的约束条件,根据真实工程应用的约束进一步提高分析的精度将作为后续工作。
References)
[1] 杨孟飞,顾斌,郭向英,等.航天嵌入式软件可信保障
技术及应用研究[J].中国科学:技术科学,2015,45(2):198-203. YANG M F,GU B,GUO X Y,et al.Aerospace embedded software dependability guarantee technology and application[J].Scientia Scinica Technologica,2015,45(2): 198-203(in Chinese).
[2] JOSEPH M,PANDYA P.Finding response times in a real-time systems[J].The Computer Journal,1986,29 (5):390-395.
[3] DAVIS R I,BURNS A.Response time upper bounds for fixed priority real-time systems[C].Real-Time Systems Symposium,Barcelona,Spain,November 30-December 3,2008.
[4] MÄKI-TURJA J,NOLIN M.Efficient implementation of tight response-times for tasks with offsets[J]. Real-time System,2008,40:77-116.
[5] BRYLOW D,PALSBERG J.Deadline analysis of interrupt-driven software[J].IEEE Transactions on Soft-ware Engineering,2004,30(10):634-655.
[6] JONATHAN K,DORSA S,SANJIT A S.Timing analysis of interrupt-driven programs under context bounds[C].Formal Methods in Computer-Aided Design, Austin,Texas,USA,October 30-November 2,2011.
[7] 王磊,袁利,戴居峰.卫星控制系统时序建模分析方法研究[J].空间控制技术与应用,2014,40(3):31-35. WANG L,YUAN L,DAI J F.Timing modeling and analysis method for satellite control system[J]. Aerospace Control and Application,2014,40(3):31-35(in Chinese).
[8] JEFFAY K,STONE D L.Accounting for interrupt handling costs in dynamic priority task systems[C]. Real-Time Symposium,NC,USA,December,1993.
[9] BRANDENBURG B B,LEONTYEV H,ANDERSON J M.An overview of interrupt accounting techniques for multiprocessor real-time systems[J].Journal of Systems Architecture,2011,57:638-654.
[10] RANDAL E BRYANT,DAVID R O′HALLARON. Computer systems:a programmer′s perspective[M].2nd ed.New Jersey:Pearson Prentice Hall,2011.
[11] SEBASTIAN A,ROBERT I D,CLAIRE M. Improved cache related preemption delay aware response time analysis for fixed priority preemptive systems[J].Real-time System,2012,48: 499-526.
[12] WILHELM R,ENGBLOM J,ERMEDAHL A,et al.The worst-case execution-time problem-overview of methods and survey of tools[J].ACM Transactions on Embedded Computing Systems,2008,7(3):1-53.
[13] SHA L,RAJKUMAR R,LEHOCZHY JP.Priority inheritance protocols:an approach to real-time synchronization[J].IEEE Transactions on Computers, 1990,39(9):1175-1185.
[14] 谭彦亮,杨桦,乔磊.基于Event-B的Space OS2操
作系统任务管理需求形式化建模与验证[J].空间控制技术与应用,2014,40(4):57-62. TAN Y L,YANG H,QIAO L.Formal modeling and verification of task-management requirement for Space OS2 based on Event-B[J].Aerospace Control and Application,2014,40(4):57-62(in Chinese).
(编辑:车晓玲)
Worst case response time analysis of multi-level interrupt systems
YU Guangliang1,*,YANG Mengfei2,XU Jian1,JIANG Hong1
1.BeijingInstituteofControlEngineering,Beijing100190,China2.ChinaAcademyofSpaceTechnology,Beijing100094,China
A computation model integrated with interrupts and tasks was presented for the analysis of worst case response time(WCRT)for an aerospace embedded system with multilevel interrupts.Both interrupts and tasks was used for a unified priority definition in this model,so the timing analysis of nested interrupts can be combined with task response time analysis techniques.The WCRT of both interrupts and tasks was derived in the integrated model.Furthermore,detailed descriptions of key parameters were proposed and the differences between interrupts and tasks were also discussed.The open source LEON3processor platform and Modelsim software were introduced to simulate and verify the method.The results show that the overestimate of task WCRT is less than 5%which demonstrates the effectiveness of the method and the value for engineering applications.
real time system;embedded software;multi-level interrupt;fixed priority scheduling;schedulability analysis;worst case response time;spacecraft
A
10.16708/j.cnki.1000-758X.2016.0003
2015-05-08;
:2015-07-27;录用日期:2015-09-28;< class="emphasis_bold">网络出版时间
时间:2016-04-19 14:46:13
http:∥www.cnki.net/kcms/detail/11.1859.V.20160419.1446.002.html
*
:于广良(1986-),男,博士研究生,yal_222@126.com,主要研究方向为航天嵌入式系统可信软件
于广良,杨孟飞,徐建,等.面向多级中断系统的任务最差响应时间分析[J].中国空间科学技术,2016,36(2): 28-36.YUGL,YANGMF,XUJ,etal.Worstcaseresponsetimeanalysisofmulti-levelinterruptsystems[J].Chinese SpaceScienceandTechnology,2016,36(2):28-36(inChinese).
:V411.8
http:∥zgkj.cast.cn

