3D FEM随钻电磁波电阻率测井响应影响因素研究

姜 明，柯式镇*，李安宗，康正明，李成远，张文豪

1中国石油大学(北京)油气资源与探测国家重点实验室，北京102200

2中国石油大学(北京)地球物理与信息工程学院，北京102200

3中国石油集团测井有限公司随钻测井仪器研究中心，西安 710061

3D FEM随钻电磁波电阻率测井响应影响因素研究

姜 明1,2，柯式镇1,2*，李安宗3，康正明1,2，李成远1,2，张文豪1,2

1中国石油大学(北京)油气资源与探测国家重点实验室，北京102200

2中国石油大学(北京)地球物理与信息工程学院，北京102200

3中国石油集团测井有限公司随钻测井仪器研究中心，西安 710061

影响随钻电磁波电阻率测井仪器响应的因素主要来自两方面:一方面是自身结构因素，包含线圈、天线凹槽、盖板、钻铤等，这些因素通过影响接收线圈感应电动势的幅度，进而对电阻率测量结果产生影响；另一方面因素来自外界环境，包括井眼泥浆、围岩、侵入、介电常数以及地层各向异性等，测井过程中的仪器响应，是对井下多种不同介质的综合响应，为了达到探测原状地层电阻率的目的，需要扣除其它因素对仪器响应的影响。因而研究影响随钻电磁波电阻率测井响应的因素，对测井资料的解释与应用是十分必要的。本文以随钻电磁波电阻率仪器WPR (Wave Propagation Resistivity)为算例，建立真实的3维仪器结构，采用3维有限元3 D FEM (Three-Dimensional Finite Element Model)方法，针对真实仪器自身结构以及外界环境因素对仪器响应造成的影响进行了数值模拟，并利用解析解对本文的数值解进行了验证。感应电动势绝对值随着线圈半径、线圈凹槽宽度、天线槽长度、盖板占空比增大而明显增大；随着凹槽深度增加而减小。其中，浅探测模式受以上因素影响较深探测模式更大。此外，感应电动势绝对值受金属钻铤的电导率影响较小。在外界环境因素方面，井眼与泥浆存在使视幅度比电阻率偏小，视相位差电阻率偏大；泥浆电阻率越大，对仪器响应造成的影响越小；各向异性使视幅度比电阻率与视相位差电阻率均偏大；泥浆侵入、围岩、介电常数以及各向异性因素使视幅度比电阻率与视相位差电阻率在数值上差异逐渐增大；泥浆侵入使视相位差电阻率与视幅度比电阻率差异先增大再减小；介电常数影响在高阻地层中更加明显，其中视相位差电阻率受影响更大。

随钻测井；随钻电磁波测井；仪器结构；环境校正；有限元

0 引言

相比传统电缆测井，随钻测井在水平井测量以及实时地质导向方面具有巨大优势，已经成为未来测井发展方向。随钻电磁波电阻率测井仪器响应不仅与地层电导率相关，还受自身仪器结构以及外界环境因素影响，其中自身结构因素主要包括线圈、天线凹槽、盖板、钻铤、填充材料等因素；环境因素主要包括井眼泥浆、围岩、侵入、介电常数以及各向异性等因素。目前有关随钻电磁波电阻率测井的数值模拟研究工作，主要围绕着仪器自身结构以及外界环境这两方面展开。但大多数研究成果是基于简化二维仪器模型，基于三维仪器结构的数值模拟研究较少，因而仪器结构影响因素往往被简化或忽视，无法准确地考察真实仪器结构对仪器响应的影响[1-19]。杨震计算了二维仪器模型下不同环境因素造成的影响[9,12]；范宜仁完成了基于时域有限差分的随钻电磁波仪器偏心条件下响应模拟与分析[10]；陈爱新采用基于加权余量法的矢量有限元方法，计算得到了水平地层环境对仪器测量结果影响趋势[13]；吴宝玉、夏宏泉等比较分析了斯伦贝谢等公司的随钻电磁波测井仪器的环境校正图版，并分析了环境影响的主次因素[14-16]；魏宝君在三维条件下采用并矢Green函数方法考察了通讯槽以及仪器偏心对仪器响应的影响[18-19]；文艺通过傅里叶-汉克尔变换法研究了层厚-井斜因素对随钻电磁波电阻率仪器响应的影响，考察了不同井斜条件下层厚与仪器响应的关系。本文以电磁波电阻率随钻测井仪WPR为算例，建立3D FEM模型，相比二维模型可以更加真实地反映仪器三维结构对测井响应的影响，系统地模拟了线圈、钻铤电阻率、天线槽、盖板等仪器自身结构因素对感应电动势绝对值大小的影响，并给出了合理的仪器设计参数；模拟了井径-泥浆、围岩-层厚、侵入、各向异性等对仪器响应的影响，给出了具有代表性的环境校正图版。

1 随钻电磁波测井仪器结构与3D FEM建模

1.1 仪器结构

电磁波电阻率测井仪器WPR采用四发双收的线圈系结构。T1、T2为上发射线圈，T3、T4为下发射线圈，接收线圈为R1、R2。线圈绕制在钻铤上的6个环形凹槽，并盖有天线盖板，盖板周向上开一系列贯穿的矩形槽口。WPR工作频率为2 MHz和400 kHz，有浅探测(T2-R1-R2，T3-R1-R2)和深探测(T1-R1-R2，T4-R1-R2)两种探测模式，其中，浅探测线圈系的发射到接收线圈的源距L=0.463 6 m，深探测线圈系的发射到接收线圈的源距L=0.806 5 m。当工作频率为2 MHz时，深探测模式下幅度比电阻率探测深度为1.12 m，相位差电阻率探测深度为0.71 m。浅探测模式下幅度比电阻率探测深度为0.87 m，相位差电阻率探测深度为0.53 m。该工作频率下垂直分辨率均为0.2 m。当目的地层电阻率为0.1～50 Ω·m时，仪器探测精度为1％，当目的地层电阻率大于50 Ω·m时，仪器探测精度为0.5 S/m。

设接收线圈R1中的感应电动势为V1，接收线圈R2中的感应电动势为V2，则实际测量记录的幅度衰减EATT和相位差φΔ分别为：

1.2 3D FEM建模与方法验证

从经典Maxwell方程、本构方程以及库仑规范出发，令：

得到如下方程：

边界条件为：

根据有限元的变分原理，泛函表达式为：

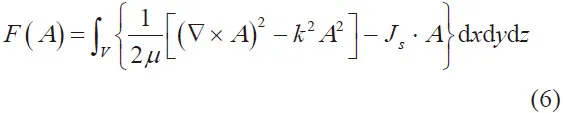
泛函(6)用离散单元可以表示为：

其中，每个单元的泛函表达式为：

将整个求解空间的所有单元的所有节点合起来形成有限元求解问题矩阵方程为：

文中计算时假设所有线圈匝数均为1匝，发射电流幅度为1 A。为了验证算法的正确性，将均匀介质的数值模拟结果与解析解进行对比，计算条件为测量频率2 MHz，线圈半径0.08 m，井眼半径8.5 inch，源距0.806 5 m。结果如图1至图2所示，图中Rt是地层真电阻率。由图可以看出幅度比信号有限元解与解析解基本吻合，相位差信号有限元解与解析解基本一致，这与文献21的计算结果也能较好地吻合，证明了本文数值算法的正确性。

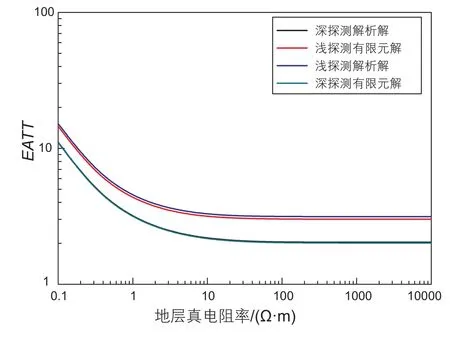
图1 幅度比信号有限元解与解析解对比Fig. 1 Amplitude ratio signal comparison between finite element and analytical solutions

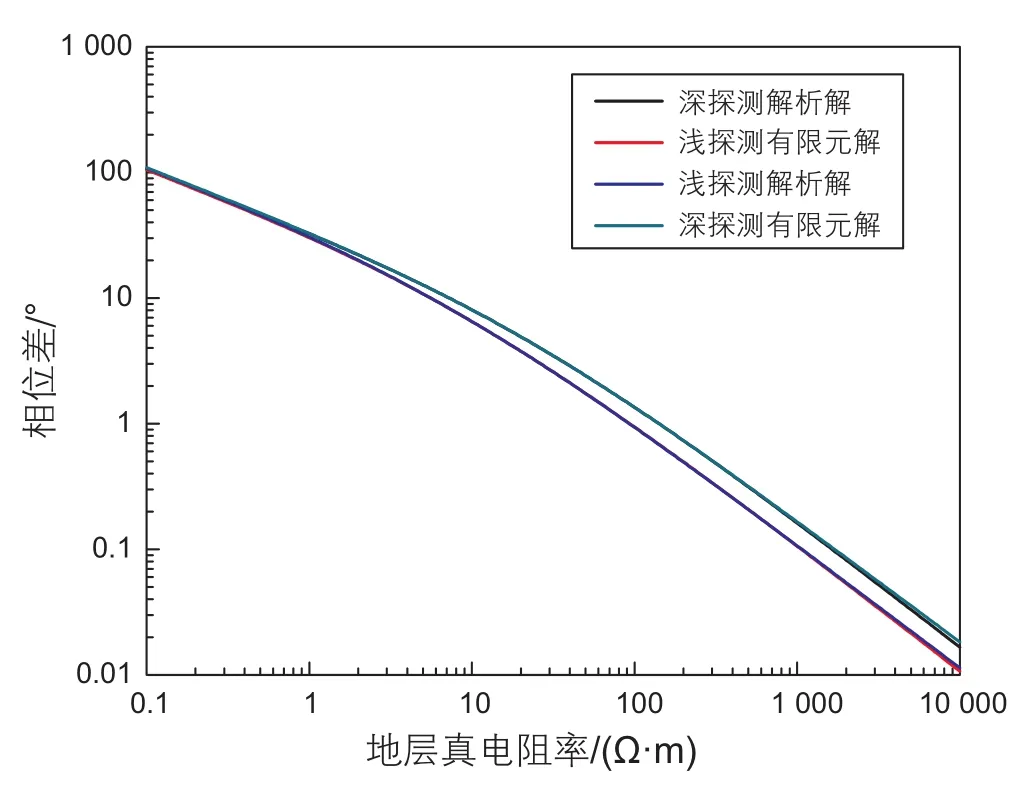
图2 相位差信号有限元解与解析解对比Fig. 2 Phase shift signal comparison between fnite element and analytical solutions

2 仪器结构数值模拟结果分析

随钻电磁波电阻率仪器线圈放置在无磁钻铤外部的环形凹槽里，外面有金属盖板保护。金属盖板周向开贯穿的天线槽，以保证电磁波信号的传播。为了防止钻井过程中泥浆岩屑侵入天线槽内，内部填充了高阻、无磁、低介电常数材料，其电学特性接近真空的电学特性，对电磁波传播影响很小，因此，对填充材料影响不展开介绍。由于幅度比EATT和相位差φΔ较难直观地反映仪器结构对电磁波信号的影响程度，因此采用接收线圈电动势绝对值对不同仪器结构影响进行评价。

2.1 线圈半径

在均匀地层模型中，分析了不同线圈半径对仪器响应的影响。浅探测与深探测模式计算结果如图3所示。图中纵坐标为仪器测得的感应电动势绝对值信号，横坐标为均匀地层电阻率。由图可知，线圈半径越大，感应电动势信号越大，即线圈接收到的电磁场能量越大。线圈半径不仅取决于钻铤尺寸，更需要考虑仪器电子线路对信号幅度的探测能力。在背景噪声一定的情况下，信噪比正比于信号幅度大小，信噪比越大对电路的要求越低。由于随钻测井环境恶劣，目前被广泛采用的信号幅度范围为μV级。由于浅探测比深探测感应电动势大，因而在选取仪器线圈半径时，应以满足深探测信号检波要求为准。在图3中，当线圈半径取0.068 m，不考虑钻铤影响时即可满足要求。

2.2 钻铤

金属钻铤采用低磁材料，可以较大程度上减少钻铤对电磁波信号的干扰。由于钻铤电导率较高，钻铤内部仍然会感生微弱的涡流，从而对接收线圈感应电动势产生影响。选取线圈半径为0.068 m，数值模拟结果如图4所示，随着钻铤电阻率增大，接收线圈电动势绝对值信号增大；当钻铤电阻率大于1 Ω·m或小于10-5Ω·m时，接收线圈感应电动势信号趋于稳定。一般情况下，随钻电磁波仪器钻铤均采用金属材料(电阻率小于10-5Ω·m)，因而接收线圈的感应电动势几乎不受仪器钻铤电阻率变化的影响。

2.3 天线凹槽

线圈放置在钻铤外部环形天线凹槽中，凹槽深度与宽度对电磁波信号的传播造成了一定影响。选取线圈半径为0.068 m，钻铤电阻率为10-5Ω·m，基于均匀地层的计算结果如图5与图6所示。由结果可以看出，当固定凹槽宽度为0.14 m时，随着线圈凹槽深度变大，深浅探测感应电动势绝对值均减小，其中浅探测幅度下降更快；当固定凹槽深度为0.022 m时，随着线圈凹槽宽度增加，深浅探测感应电动势绝对值均随凹槽宽度增大而增大，其中浅探测增大幅度大于深探测。可以看出凹槽深度小于0.03 m，宽度大于0.08 m时，感应电动势信号幅度大于10 μV，满足仪器设计要求。

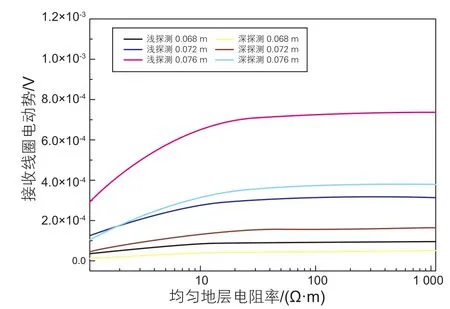
图3 不同线圈半径下地层电阻率与接收线圈电动势的关系Fig. 3 Relations between induced voltage and radius of the coil at different coil radius

图4 钻铤电阻率影响Fig. 4 Effects of metal mandrel resistivity

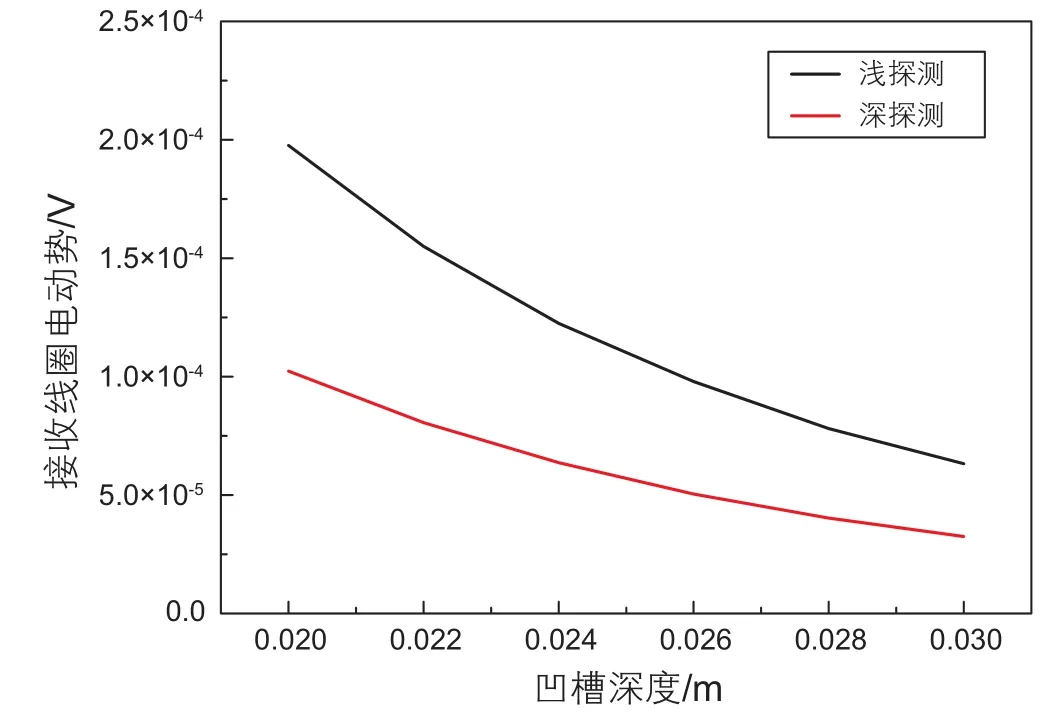
图5 凹槽深度影响Fig. 5 Effects of groove depth

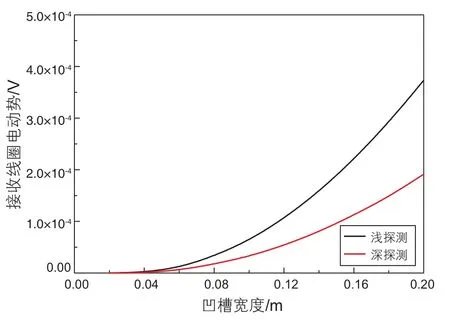
图6 凹槽宽度影响Fig. 6 Effects of groove width

2.4 盖板

线圈盖板采用金属材料，高电导率材料对电磁波信号屏蔽效果明显，为此在盖板周向上开一系列天线槽。假设线圈半径为0.068 m，钻铤电阻率为10-5Ω·m，凹槽深度为0.022 m，宽度为0.14 m，盖板结构影响的数值模拟结果如图7到8所示。其中图7表示当固定占空比为50％时，天线槽长度对感应电动势的影响，图8表示当固定天线槽长度为0.1 m时，占空比对感应电动势的影响。由图中结果可以看出，当分别固定占空比或天线槽长度时，随着天线槽长度或占空比增加，感应电动势绝对值均增大，其中占空比因素对信号幅度影响较大，天线槽长度影响较小。实际应用时，在满足机械强度与电子线路检波要求下，占空比应在15％～50％之间，天线槽长度应在0.08 m以上。

3 外界环境数值模拟分析

外界环境因素主要包括井眼泥浆、围岩、侵入、偏心以及各向异性。以下计算时假设所有线圈匝数均为1匝，发射电流强度为1 A，线圈半径均取0.068 m，钻铤电阻率为10-5Ω·m，仪器直径为0.178 m，凹槽深度为0.022 m，凹槽宽度为0.14 m，天线槽长度为0.15 m，盖板占空比为30％。

图7 天线槽长度影响Fig. 7 Effects of slot length

图8 盖板占空比影响Fig. 8 Effects of space proportion of cover

图9 井眼泥浆影响(深探测幅度比电阻率，Rm=0.5 Ω·m, f=2 MHz)Fig. 9 Effects of borehole-mud (amplitude ratio deep resistivity, Rm=0.5 Ω·m, f=2 MHz)

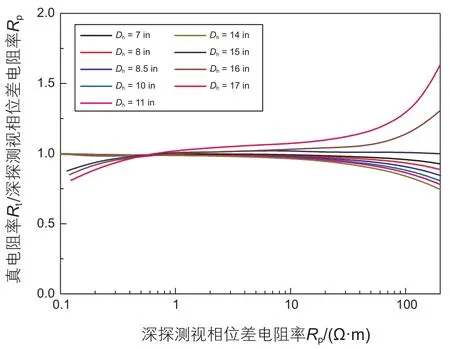
图10 井眼泥浆影响(深探测相位差电阻率，Rm=0.5 Ω·m, f=2 MHz)Fig. 10 Effects of borehole-mud (phase shift deep resistivity, Rm=0.5 Ω·m, f=2 MHz)

3.1 井径与泥浆

井眼直径以及泥浆电阻率变化，对电磁波电阻率仪器响应造成影响。在均匀地层模型中，计算了泥浆电阻率{0.05、0.1、0.2、0.5、1、2、5 Ω·m}范围内时，井径变化对视电阻率的影响。其中探测频率为2 MHz，泥浆电阻率为0.5 Ω·m时，深探测视电阻率计算结果如图9与图10所示。图中横坐标为视幅度比电阻率或视相位差电阻率，纵坐标为真电阻率与视电阻率比值。图中，Dh为井眼直径，单位为英寸。可以看出，泥浆电阻率与地层电阻率对比度越大，泥浆影响越明显。井眼因素使视幅度比电阻率偏小，视相位差电阻率偏大，但在井径较大时，视相位差电阻率开始偏小。当泥浆电阻率增大时，井径与泥浆对视电阻率影响变小，原因是较高电阻率的泥浆对电磁波的衰减能力减弱，因而幅度衰减与相位移也较小，所以高阻泥浆对视电阻率影响较小。

3.2 围岩-层厚

垂直井中，井眼轴向上岩性剖面常由不同岩性和厚度的地层组成。围岩层和目的层的电阻率差异将会影响视电阻率值，在均匀三层地层模型中，计算了{0.5、1、2、4、6、8、10、15、20、30、40、50 Ω·m}范围内12种不同围岩电阻率条件下，围岩对视电阻率的影响。其中围岩电阻率为10 Ω·m时计算结果如图11和图12所示，图中目的层厚度变化范围为0.5～10 m，视电阻率范围为0.2～500 Ω·m。可以看出随目的层厚度不断增大，仪器受围岩影响逐渐减小；视幅度比电阻率受围岩影响较大，视相位差电阻率受围岩影响较小，且其薄层响应更加接近真电阻率；目的层为高阻薄层时，视电阻率受低阻围岩影响较大，这使得视电阻率明显小于真电阻率。

图11 围岩-层厚影响(深探测幅度比电阻率，Rs=10 Ω·m, f=2 MHz)Fig. 11 Effects of surrounding rock and thickness (amplitude ratio deep resistivity, Rs=10 Ω·m, f=2 MHz)

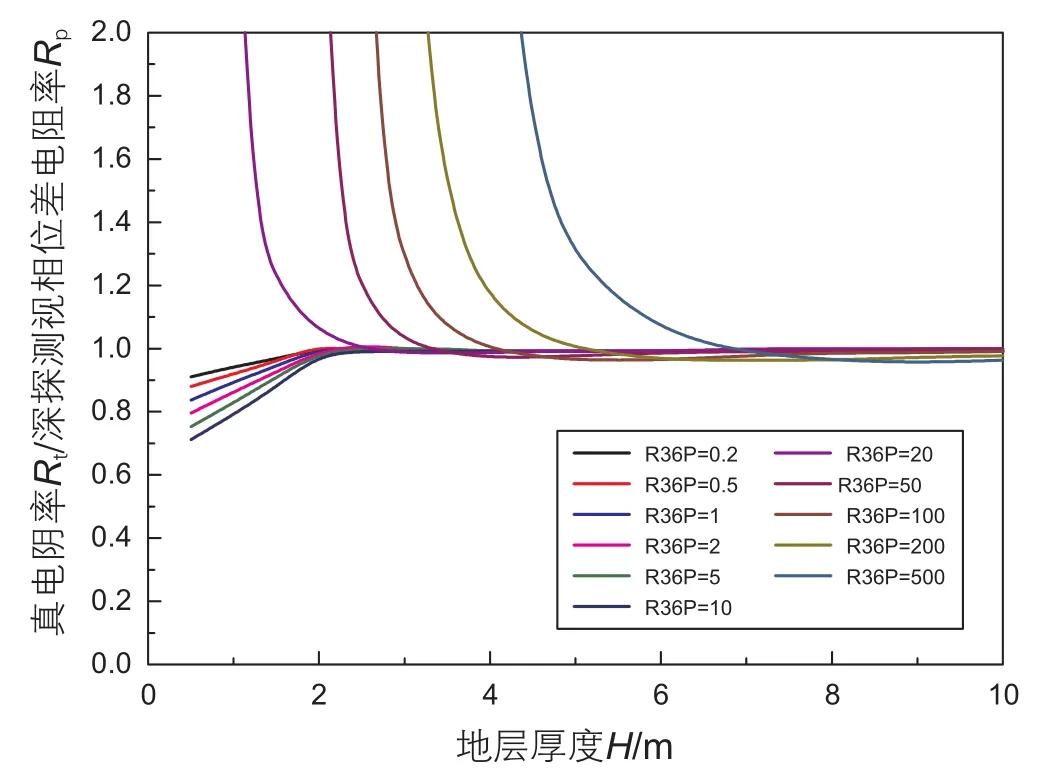
图12 围岩-层厚影响(深探测相位差电阻率，Rs=10 Ω·m, f=2 MHz)Fig. 12 Effects of surrounding rock and thickness (phase shift deep resistivity, Rs=10 Ω·m, f=2 MHz)

3.3 侵入带

国内外有关随钻电磁波电阻率测井侵入校正图版研究较少。本文依据幅度比电阻率与相位差电阻率的差异，以及冲洗带电阻率3个参数作为随钻电磁波电阻率侵入校正依据。假设地层轴向均匀且无井眼影响，地层无限厚。侵入深度Di变化范围为10～40英寸，地层电阻率Rt变化范围为0.1～500 Ω·m。计算了{1、2、5、10、20、50 Ω·m}范围内6种不同侵入带电阻率情况下的侵入校正图版。其中当侵入带电阻率Rxo=1 Ω·m时，深探测模式下，2 MHz工作频率时，计算结果如图13所示。

当Rxo/Rt＞1时(即井眼泥浆高侵)，视电阻率大于真实地层电阻率。此时视相位差电阻率大于视幅度比电阻率，随着侵入半径的增大，视相位差电阻率与视幅度比电阻率的差异先增大后减小(当侵入深度达到一定程度后，视幅度比与视相位差电阻率受到侵入影响相当)。当Rxo/Rt＜1时(即井眼泥浆低侵)，视电阻率小于真实地层电阻率。此时视相位差电阻率小于视幅度比电阻率，随着侵入半径的增大，视相位差电阻率与幅度比视电阻率的差异同样先增大后减小(当侵入深度达到一定程度后，视幅度比与视相位差电阻率受到侵入影响相当)。

3.4 介电常数

由于泥浆与地层的介电常数影响，导致视幅度比电阻率与视相位差电阻率在数值上散开，其中视幅度比电阻率较真电阻率偏大，视相位差电阻率偏小。实际测量过程中，含水砂岩存在介电频散现象，在低频测量段时(主要为10 MHz以下)，由于多种极化机制的叠加导致实际测得的相对介电常数出现高值[22-23]。

基于无井眼均匀地层模型，介电常数影响的计算结果如图14与15所示，图中相对介电常数变化范围为1～1 000 F/m。显然相比400 kHz测量频率，2 MHz测量频率更易受到介电影响，仅对仪器测量频率为2 MHz时，深探测受介电常数影响的计算结果进行介绍。由图中可以看出，当地层电阻率增大时，仪器响应受介电常数影响也变大。相对于幅度比电阻率，相位差电阻率受介电常数影响更大。介电影响使视幅度比偏大，视相位差电阻率偏小。

图13 侵入影响(Rxo=1 Ω·m, f=2 MHz)Fig. 13 Effects of invasion (deep investigation, Rxo=1 Ω·m, f=2 MHz)

图14 介电常数影响(深探测幅度比电阻率，f=2 MHz)Fig. 14 Effects of permittivity (amplitude ratio deep resistivity, f=2 MHz)

图15 介电常数影响(深探测相位差电阻率，f=2 MHz)Fig. 15 Effects of permittivity (phase shift deep resistivity, f=2 MHz)

3.5 各向异性

随钻测井过程多数情况会遇到各向异性地层。各向异性是指由于目的地层厚度小于仪器纵向分辨率，或者仪器与地层存在相对夹角导致水平电阻率(RH)与垂直电阻率(RV)不一致的现象。

当目的地层厚度小于仪器纵向分辨率时，视电阻率受水平电阻率与垂直电阻率对比度RV/RH影响。选取水平目的层真电阻率为1 Ω·m，仪器与水平地层相对倾角为65°，视电阻率与RV/RH关系如图16与17。可以看出，RV与RH的差异使视幅度比电阻率与视相位差电阻率均比水平目的层真电阻率偏大，二者随着RV/ RH增大而散开。其中视幅度比电阻率受RV/RH影响较小，且不同频率的视幅度比电阻率受RV/RH影响几乎相同；而不同频率的视相位差电阻率受RV/RH影响程度不同，其中2 MHz视相位差电阻率受影响较大。

图16 各向异性影响(RV/RH，深探测幅度比电阻率，65°)Fig. 16 Effects of anisotropy (RV/RH, amplitude ratio deep resistivity, 65°)

图17 各向异性影响(RV/RH，深探测相位差电阻率，65°)Fig. 17 Effects of anisotropy (RV/RH, phase shift deep resistivity, 65°)

图18 各向异性影响(相对倾角，深探测幅度比电阻率，RV/RH=4)Fig. 18 Effects of anisotropy (relative dip angle, amplitude ratio deep resistivity, RV/RH=4)

图19 各向异性影响(相对倾角，深探测相位差电阻率，RV/RH=4)Fig. 19 Effects of anisotropy (relative dip angle, phase shift deep resistivity, RV/RH=4)

对于由相对倾角引起的各向异性，存在类似规律，选取水平目的层真电阻率为1 Ω·m，固定RV/RH=4，改变相对倾角，规律如图18与19，即视幅度比电阻率与视相位差电阻率均偏大，其中视相位差电阻率受倾角影响更大。不同频率的视幅度比电阻率受相对倾角影响的差异不明显，而不同频率视相位差电阻率差异明显。

4 结论

感应电动势绝对值随着线圈半径、线圈凹槽宽度、天线槽长度、盖板占空比增大而明显增大；随着凹槽深度增加而减小。其中浅探测模式受以上因素影响较深探测模式更大。此外，感应电动势绝对值受金属钻铤的电导率影响较小。

井径与泥浆因素，使得视幅度比电阻率偏小；视相位差电阻率偏大(井径较大时开始偏小)；当泥浆电阻率增大时，泥浆对视电阻率影响变小；视幅度比电阻率受围岩影响较大，视相位差电阻率受围岩影响较小；当泥浆高侵时，视相位差电阻率大于视幅度比电阻率；当泥浆低侵时，视相位差电阻率小于视幅度比电阻率；随着侵入半径增大，视相位差电阻率与幅度比视电阻率的差异先增大后减小；当地层电阻率增大时，仪器响应受介电常数影响变大；视相位差电阻率受介电常数影响更大；由地层的各向异性，使得视幅度比电阻率与视相位差电阻率均偏大，其中视幅度比电阻率比相位差电阻率受到的影响较小。各向异性对不同频率的视相位差电阻率影响差异较大，对不同频率的视幅度比电阻率影响差异较小。

[1]ANDERSON B, BARBER T, LLING M, et al. Observations of large dielectric effects on LWD propagation-resistivity logs[C]. SPWLA 48thAnnual Logging Symposium, Austin, 2007.

[2]DAVYDYCHEVA S, DRUSKIN V, HABASHY T. An effcient fnite-difference scheme for electromagnetic logging in 3D anisotropic in homogeneous media [J]. Geophysics, 2003, 68(5): 1525-1536.

[3]DYATLOV G, ONEGOVA E, DASHEVSKY Y. Efficient 2.5D electromagnetic modeling using boundary integral equations [J]. Geophysics, 2015, 80(3): E164-E173.

[4]LI J. Comparing tool eccentricity effects on LWD propagation resistivity for oil-based and waterbased muds[J]. Seg Technical Program ExpandedAbstracts, 2008, 27(1): 3713.

[5]JACKSON C, HAGIWARA T. A new simultaneous anisotropy and dielectric correction algorithm for LWD resistivity measurements[C]. SPWLA 39th Annual Logging Symposium, Houston, 1998.

[6]MEYER W H. Analysis of environmental corrections for propagation resistivity tools[J]. SPWLA 41th Annual Logging Symposium, Houston, 2000.

[7]MICHAEL S. BITTAR, HU H Y, et al. The effects of rock anisotropy on LWD toroidal resistivity sensors[C]. SPWLA 44th Annual Logging Symposium. Houston, 2004.

[8]YANG J, OMERAGIC D, LIU C, et al. Bed-Boundary effect removal to aid formation resistivity interpretation from LWD propagation measurements at all dip angles[C]. SPWLA 46th Annual Logging Symposium. New Orleans, 2005.

[9]杨震, 杨锦舟, 韩来聚.随钻电磁波电阻率测井实时井眼影响校正[J].石油勘探与开发, 2013, 40(5): 625-629. [YANG Z, YANG J Z, HAN L J. A real-time borehole correction of electromagnetic wave resistivity logging while drilling[J]. Petroleum Exploration and Development, 2013, 40(5): 625-629.]

[10]范宜仁, 胡云云, 李虎, 等.随钻电磁波测井仪器偏心条件下响应模拟与分析[J].中国石油大学学报(自然科学版), 2014, 38(2): 59-66. [FAN Y R, HU Y Y, LI H, et al. Numerical modeling and analysis of responses of eccentric electromagnetics logging while drilling tool[J]. Journal of China University of Petroleum (Edition of Natural Science), 2014, 38(2): 59-66.]

[11]宋殿光, 段宝良, 魏宝君, 等.金属钻铤对随钻电磁波电阻率测井仪测量信号的影响[J].测井技术, 2014, 38(2): 201-205. [SONG D G, DUAN B L, WEI B J. The Infuence of metal mandrel on electromagnetic resistivity logging responses[J]. Well Logging Technology, 2014, 38(2): 201-205.]

[12]杨震, 刘庆成, 岳步江, 等.随钻电磁波电阻率测井仪器响应影响因素数值模拟[J].测井技术, 2011, 35(4): 325-330. [YANG Z, LIU Q C, YUE B J, et al. Numerical simulation on infuence factors of electromagnetic wave resistivity logging while drilling response[J]. Well Logging Technology, 2011, 35(4): 325-330.]

[13]陈爱新.随钻电磁波测井环境影响分析[J].石油地球物理勘探, 2006(5): 601-605. [CHEN A X. Electromagnetic logging-while-drilling environmental impact analysis[J]. Geophysical Prospecting For Petroleum, 2006(5): 601-605.]

[14]吴宝玉, 夏宏泉, 张智勇.随钻电阻率测井的围岩影响及校正方法研究[J].西南石油学院学报, 2006, 28(6): 20-23+112-113. [WU B Y, XIA H Q, ZHANG Z Y. Effect of shoulder beds on resistivity logging while drilling and its correction method[J]. Journal Of Southwest Petroleum Institute, 2006, 28(6): 20-23+112-113.]

[15]刘红岐, 夏宏泉, 郭璞, 等.随钻电阻率测井介电效应校正图版分析及方法[J].西南石油大学学报: 自然科学版, 2010, 32(2): 58-62+198. [LIU H Q, XIA H Q, GUO P, et al. Study on the correction chart for dielectric effect of resistivity logging while drilling[J]. Journal Of Southwest Petroleum University (Science & Technology Edition), 2010, 32(2): 58-62+198.]

[16]夏宏泉, 刘之的, 朱猛, 等.随钻电阻率测井的环境影响校正主次因素分析[J].测井技术, 2008, 32(2): 159-163. [XIA H Q, LIU Z D, ZHU M, et al. Analysis of the primary and secondary environmental effects correction on LWD resistivity log[J]. Well Logging Technology, 2008, 32(2): 159-163.]

[17]刘国胜, 杨海东, 汤健超.复杂地质层中电磁波测井响应特性的数值研究[J].中南大学学报: 自然科学版, 2013, 44(2): 656-661. [LIU G S, YANG H D, TANG J C. Numerical investigation for responses of electrical logging-while-drilling in complex formations[J]. Journal of Central South University(Science and Technology), 2013, 44(2): 656-661.]

[18]魏宝君, 徐丹, 王莎莎.通讯槽对电磁波传播随钻测量信号的影响[J].中国石油大学学报: 自然科学版, 2011, 35(1): 56-60. [WEI B J, XU D, WANG S S. Infuence of communication slots on signal of electromagnetic propagation measurement while drilling[J]. Journal of China University of Petroleum (Edition of Natural Science), 2011, 35(1): 56-60.]

[19]魏宝君, 田坤, 张旭, 等.用并矢Green函数的矢量本征函数展开式评价偏心对随钻电磁波电阻率测井响应的影响[J].中国石油大学学报: 自然科学版, 2010, 34(5): 57-62. [WEI B J, TIAN K, ZHANG X, et al. Evaluating infuence of eccentricity on response of electromagnetic wave resistivity logging-while-drilling by vector eigenfunction expansion formulae for dyadic Green’s functions[J]. Journal of China University of Petroleum (Edition of Natural Science), 2010, 34(5): 57-62.]

[20]文艺, 韩晓梅.大斜度井随钻电磁波层厚影响模拟及机理分析[J].西南石油大学学报(自然科学版), 2013, 35(04): 75-80. [WEN Y, HAN X M. Simulation of bed thickness effect and mechanism analysis of electromagnetic wave resistivity logging while drilling in highly-deviated wells. Journal Of Southwest Petroleum University (Science & Technology Edition), 2013, 35(04): 75-80.]

[21]范宜仁, 李炜, 李虎, 等.基于时域有限差分亚网格与共形网格技术的随钻电磁波测井响应数值模拟[J].测井技术, 2015, 39(5): 561-566. [FAN Y R, LI W, LI H, et al. Numerical simulation of electromagnetic LWD response based on subgridding algorithm and conformal FDTD[J]. Well Logging Technology, 2015, 39(2): 561-566.]

[22]MEHDI. H, HENRI. B, BENOIT D, et al. Dielectric dispersion: A new wireline petrophysical measurement [C]. SPE Annual techogic Conference. and Exhibition, Denver, 21-24 September 2008.

[23]赵淑芳.高频场中岩石介电性质的实验研究[J].石油学报, 1982(s1): 63-72. [ZHAO S F. Study of dielectric properity of rocks in a high-frequency feld[J]. Acta Petrolei Sinica, 1982(s1): 63-72.]

Factors effecting simulation of the response of LWD electromagnetic wave resistivity based on 3D FEM

JIANG Ming1,2, KE Shizhen1,2, LI Anzong3, KANG Zhengming1,2, LI Chengyuan1,2, ZHANG Wenhao1,2
1 State Key Laboratory of Petroleum Resources and Prospecting, China university of petroleum, Beijing 102200, China
2 College of Geophysics and Information Engineering, China university of petroleum-Beijing, Beijing 102200, China
3 China Petroleum Logging Co. Ltd., Xi’an 710061, China

Both of the structure of logging tools and environmental factors affect the response of LWD (Logging While Drilling) electromagnetic wave resistivity tools. The structures of the receiver coil, coil groove, coil cover and metal mandrel impact on the amplitude of the induced voltage in the receiver coil, and the measurements of resistivity are affected indirectly. In terms of environment factors, the responses of borehole-mud, surrounding rock, drilling fuid invasion, dielectric properties and anisotropy contribute to the real response of logging tools. These responses corresponding to environment factors should be removed to obtain the real response of the undisturbed formation. Thus, it is indeed imperative to study the effects of tool-structure and environments factors for the interpretation and application of logging information. In this paper, an example of numerical simulation of a wave propagation resistivity tool based on a 3D FEM (Three-dimensional Finite Element Model) method is introduced. We have conducted the numerical simulation of the tool-structure and environments factors based on the real structure of the logging tools. The absolute value of the induced voltage rapidly increases with an increase of coil radius, width of coil groove, length of coil slot, and space proportion of cover. The absolute value decreases with an increase of the depth of the coil groove. The shallow mode is more susceptible than the deep mode to the above factors. Moreover, the absolute value has a weak relation with the conductivity of the metal drill collar. In the respect of environmental factors, the apparent amplitude ratio resistivity decreases while the apparent phase shift resistivity increases due to the borehole-mud while the effects of mud become weaker as the mudresistivity increases; both in the apparent amplitude ratio and the apparent phase shift resistivity increase due to the anisotropy. The value difference between the apparent amplitude ratio and apparent phase shift resistivity increases owing to the effects of the mud invasion, surrounding rock, dielectric or anisotropy. The difference of the two above resistivity values increases at frst, and then decreases due to the effect of mud. The infuence of dielectric properties becomes more signifcant in high resistivity formations. Apparent phase shift resistivity is more sensitive than the apparent amplitude ratio resistivity for dielectric effects.

LWD; electromagnetic propagation resistivity logging; tool structure; environment correction; fnite element model

2016-07-06

国家油气重大专项(2011ZX05020-002)资助

10.3969/j.issn.2096-1693.2016.03.029

(编辑 付娟娟)

姜明, 柯式镇, 李安宗, 康正明, 李成远, 张文豪. 3D FEM随钻电磁波电阻率测井响应影响因素研究. 石油科学通报, 2016, 03: 342-352

JIANG Ming, KE Shizhen, LI Anzong, KANG Zhengming, LI Chengyuan, ZHANG Wenhao. Factors effecting simulation of the response of LWD electromagnetic wave resistivity based on 3D FEM. Petroleum Science Bulletin, 2016, 03: 342-352. doi: 10.3969/ j.issn.2096-1693.2016.03.029

*通信作者, wksz@cup.edu.cn