铁路网多流向超限货物运输路径优化模型及算法

陈 皓， 王文宪， 李雪芹

（1．西南交通大学交通运输与物流学院，四川成都610031；2．综合交通运输智能化国家地方联合工程实验室，四川成都610031）

铁路网多流向超限货物运输路径优化模型及算法

陈 皓1，2， 王文宪1， 李雪芹1

（1．西南交通大学交通运输与物流学院，四川成都610031；2．综合交通运输智能化国家地方联合工程实验室，四川成都610031）

为了将铁路网中具有不同去向的超限货物合理地分配至各条路径，以超限货物的运输路径里程、运输时间以及对既有线路正常运营组织干扰最小为目标，以路段运输限界、通过能力和途经桥梁乘载能力为约束，建立多流向超限货物运输路径选择的多目标规划模型．根据模型特点设计多目标混合遗传算法进行求解，该算法采用自然数组编码方式以及特殊的交叉、变异算子用以满足约束条件，同时引入模拟退火策略提高邻域搜索能力．实例结果表明，对于包含14个节点车站、23个路段的复杂铁路网，利用本文模型算法获得方案的目标函数值均优于遗传算法和退火算法得到的方案，从而为铁路网超限货物运输路径选择提供技术决策方法．

超限货物；路径优化；非线性混合整数规划模型；混合遗传算法

Key words：out-of-gauge freights；path optimization；nonlinear mixed integer programming model；ant colony algorithm

超限超重货物多数是国家基础建设设施或大型机械设备，具有长大、笨重的特征，且具有极高的价值．这就决定了超限超重货物运输的特点是高费用、高风险、高复杂度的作业过程．特别是在组织超限超重专列进行运输时，其运输过程需要调度、车辆、机务、工务、电务等多个铁路运输部门协同完成．这就使得超限超重货物的运输条件比普通货物更严格［1-2］．本文对铁路网多流向超限货物运输问题的界定是，将具有不同来源或去向的超限货物分配在铁路网中的不同运输路径上，其实质为货物运输路径选择问题．

针对该问题，国内外学者做过较多相关研究．文献［3］用双目标双容量数学模型求解超限超重货物的运输路径选择，将该问题转化成具有最大流限制的最短路径问题，并设计了求解该问题的算法．文献［4-5］综合考虑限界、桥梁承载能力、车流平衡等约束，以对正常运输组织干扰、运输里程和费用最小化为目标，构建了超限超重货物运输路径优化模型，设计了基于不断修正规范化目标函数权重的实例匹配策略，构造了启发式路径搜索算法．文献［6］深入分析了超限车运行决策优化问题，根据超限车装载加固实例匹配原理，构建超限车运行决策网络模型，并提出超限车运行决策优化算法，有效解决了超限车运行决策优化问题．文献［7］采取层次分析法，对超限超重货物运输中的突出问题进行了权重分析，并针对这些问题建立了应急预案的基本框架和应急响应体系，提出了突发事件的应急措施、应急预案的编制与实施方法，对超限超重货物运输方案的设计过程实例进行了分析．文献［8］建立了超限超重货物运输影响因素的模糊综合评价模型，设计了优化算法的思想，应用模糊数学思想设计了单层和多层路径决策模型，并给出了相应的单层和多层路径决策优化算法．

上述研究主要是通过建立各种超限货物路径选择模型，设计不同启发式算法实现路网最优路径的搜索．但随着路网规模的扩大，以及线路区间运输组织的复杂化，获取该问题的精确解具有相当的难度．根据超限货物运输的特性及铁路运输状况设计相应的高效启发式算法，是提高求解效率的重要策略．遗传退火算法是在遗传算法的基础上，用模拟退火策略以增强邻域搜索能力的混合优化算法，即引入模拟退火Metropolics选择机制作为另一个算子的改进算法．对于模拟退火的研究已有较多成果．文献［9］使用混合遗传-模拟退火算法对公交行车调度进行优化，表明该算法比标准遗传算法具有更高的效率．文献［10］提出改进遗传模拟退火算法，对大件公路运输路径选择问题进行优化，实例仿真验证了该算法相对于其他算法的优越性．

本文在上述研究的基础上，综合考虑路段区间的铁路限界、桥梁承载能力与线路通过能力等约束，以及对正常运输组织的干扰，对运营里程、运输时间进行综合优化，建立多流向超限超重货物运输径路综合优化模型．在融合遗传算法并行计算能力以及模拟退火算法邻域搜索优势的基础上，设计改进的混合算法求解模型，从而快速确定各流向超限超重货物的运输路径．

1 模型构建

超限货物运输网络是运输路径优化的基础，铁路网

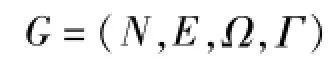
中，铁路网中的车站节点和连接线路分别为网络顶点和有向弧．

车站节点集

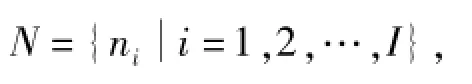
I表示车站节点的数量；连接车站节点i和j的线路集

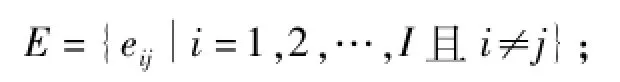
线路的能力属性集

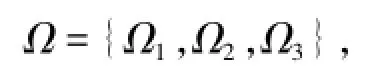
包括线路的综合最小建筑限界、桥梁检定承载系数以及通过能力；线路的广义运输属性集

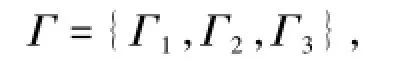
包括线路的运输密度、运输里程以及运输速度．铁路网超限货物运输路径优化模型M1为

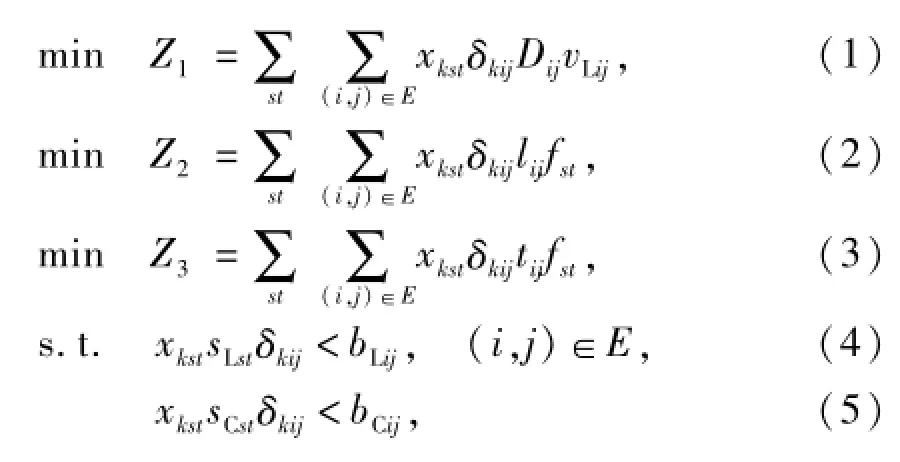
式中：fst为s→t流向的超限货物运量；

K为超限货物列车的平均编成辆数；

sLst为超限货物装载后在直线线路上的轮廓；

sCst为超限货物装载后在曲线线路上的轮廓；

Qst为超限货物列车通过桥梁的运行活载；

δkij为某流向超限货物的运输路径与区间i→j的关联系数，取1表示区间i→j在其运输路径上，取0为否；

bLij为区间i→j上的最小直线建筑限界；

bCij为区间i→j上的最小曲线建筑限界；

mij为区间i→j的最小桥梁承载系数；

Cij为区间i→j的通过能力；

cij为区间i→j的原有列车数；

Dij为区间i→j的运输密度；

vLij为超限货车在区间i→j的限速；

lij为区间i→j的里程；

Tij为区间i→j的单位运输时间；

xkst为0-1决策变量，取1时表示s→t流向的超限货物选取路径pkst，取0为否，

Pst为s→t流向超限货物的可行路径集．

式（1）表示对正常运输组织干扰最小的目标函数．由于开行超限超重的货运列车，需要铁路多部门的合作协调，运输组织极为复杂．例如，超限等级或重心较高时，有严格的限速且不能会车等，这些因素会对原有线路运输车辆的正常运营造成极大的影响．所以开行这类超限超重货车，需要尽量避开主要干线或繁忙线路，尽可能地减少对现有线路运输组织的影响．在此用对线路正常情况下运输密度的干扰程度来表示开行超限超重货车对正常运输组织的影响，干扰程度与超限货车的限速有关，限速越小，干扰越大［13］．

式（2）表示运输里程短的目标函数．在尽可能满足约束条件的前提下，最短运输路径是指相对较短，而非绝对的最短路径．

式（3）表示运输时间短的目标函数．在一些线路条件较差的地方，如果进行超限超重货物列车的运输，由于超限等级、线路线间距、曲线半径等因素的限制，超限货物列车需要限速通过．

超限超重货物由于其运输货物的特殊性，对运输路径选择的要求更为苛刻，为保障运输安全，除了要满足一般货物运输所需考虑的车流平衡和站线能力约束，还应考虑其它安全方面的约束要求［11-12］．

式（4）和（5）表示限界限制约束条件．运输限界限制了该线路允许通过车辆的尺寸范围，尤其是超宽、超高、超长的货物运输，在直线或曲线线路上，货物任意位置的尺寸必须严格地与实际建筑限界保持一定的距离．

式（6）表示桥梁承载能力限制约束条件．桥梁的承载能力应以桥梁的检定承载系数表示，车辆在通过桥梁或线路时，车辆重量必须小于或等于该段线路或桥梁所允许的检定承载系数．

式（7）表示区间通过能力限制约束条件．超限货物列车通过某区间，与该区间原有车流量的总和不得超过该区间的通过能力．

2 混合遗传算法设计

在上述多目标优化问题中，这些子目标之间并非正相关，很难找到一组解使多目标优化模型的各子目标同时达到最优，通常只能求得模型的非劣解，即Pareto最优解．

2．1 多目标优化的概念

对于具有α个子目标的多目标优化问题

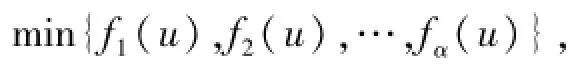
如果u、v分别为该问题的两个可行解，其对应的各子目标的目标函数值记为

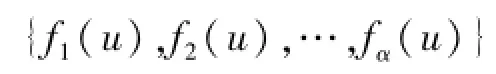
和

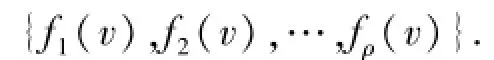
定义1 Pareto占优．当且仅当∀δ＝1，2，…，α，fρ（u）≤fρ（v），且∀β＝1，2，…，α，fβ（u）＜fβ（v）时，可行解u对于可行解v占优．

定义2 Pareto最优．设u*为可行解，其目标函数为｛f1（u*），f2（u*），…，fα（u*）｝，对于所有u，不存在fρ（u）＜fρ（u*），则称可行解u*为Pareto最优解．

2．2 算法设计

遗传退火算法的基本思路是，首先随机产生初始种群，执行完基本遗传算子后，按照某种策略生成邻域种群，然后针对两种群个体分别执行Metropolics选择，并下降温度．本文借鉴SA-GA（simulated annealing-genetic algorithm）算法机理，对算子进行适当修改，应用于求解铁路网超限货物运输路径决策问题．

（1）编码方式

一般来说，运用遗传算法解决组合优化问题时，应将该问题的解编码为一个具有某种设计规则的自然数组［14］．本文用向量Schrom＝（p1，p2，…，pm）作为一个染色体来表示从1～m流向超限货物的各运输路径，其中，染色体中的每个基因片段pi（i＝1，2，…，m）都对应该流向超限货物所经过的路径，即pi＝（r1，r2，…，rn）．

（2）适应度函数

个体适应度主要由目标函数值决定，在本文中，每条染色体都具有3个适应度值，即对正常运输组织干扰、运输里程与运输时间的适应度分别为

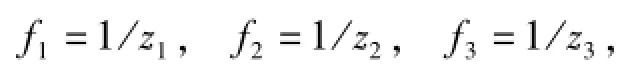
式中：z1～z3为模型M1的目标函数．．

对于超出限界限制的区段，引入惩罚系数M和阶跃函数J（x）．定义

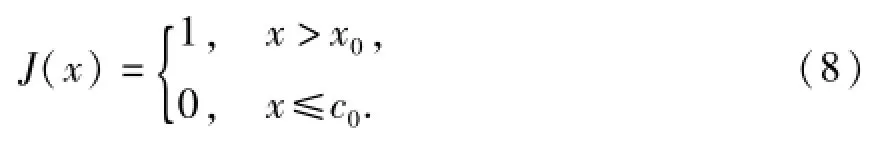
将式（8）代入目标函数，即

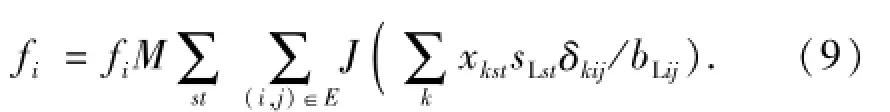
可采用上述方法将桥梁承载与区间通过能力限制约束条件转化为虚拟路段能力．

（3）选择方式

本文采取保留精英的选择策略，首先根据适应度函数选择种群中具有最优适应度的个体直接进入子代，再对当前种群执行随机遍历抽样，直至子代种群规模与父代相同．

（4）交叉方式

交叉方式如图1所示．在染色体中随机选择两个不同流向超限货物所选路径的代表基因片段（n1，n2，…，nn）和，并随机选择它们之间的某个公共节点，即ni＝n′i，交换两个基因片段在该节点后的部分染色体，从而得到两个新的染色体：

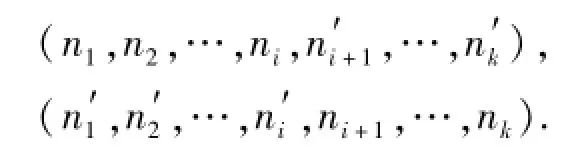
图1 交叉方式Fig．1 Cross mode

（5）变异方式

在对染色体进行变异时，首先随机选择某个流向超限货物所代表的基因片段，然后在｛1，2，…，k｝中随机产生一个整数i，再寻找一条从节点ni～nI的路径

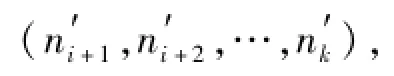
从而得到一条新的染色体

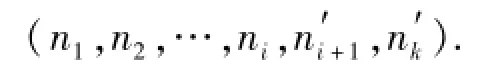
（6）模拟退火策略

在混合遗传算法中，遗传算法控制全局的寻优方向，模拟退火的Metropolics邻域搜索策略提高算法的邻域搜索能力，两者结合使算法的求解性能得到提高．

每次迭代时，在执行完遗传策略的子代种群中，随机选择一个当前个体Schromi并按照变异的方式产生其邻域个体Schromj，然后按照Metropolics策略对当前个体进行替换：

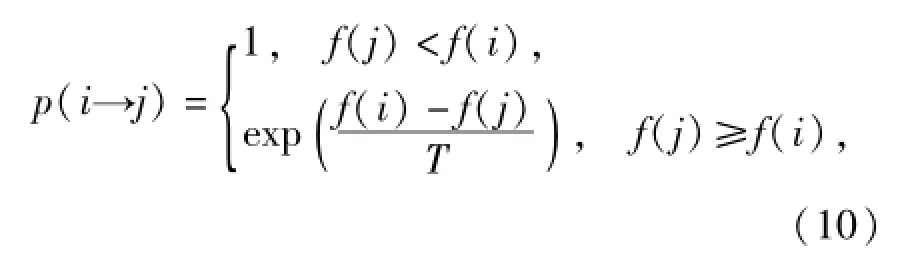
式中：p（i→j）为当前个体Schromi被邻域个体Schromj替换的概率；

f1（i）、f2（i）为当前个体Schromi的适应度；

T为当前温度．

用遗传算法求解超限货物运输路径优化问题的流程如下．

步骤1 设定参数，种群大小为popsikze，交叉概率调整参数为pc，变异概率为pm，最大迭代次数为Gmax；

步骤2 按照本节文染色体编码方式生成初始种群pop，当前代数g←1；

步骤3 计算当前种群中各染色体的适应度，根据本节设计的选择规则生成父代种群；

步骤4 根据本节设计的交叉方式，对种群进行交叉操作；

步骤5 根据前文设计的变异方式，对种群进行变异操作；

步骤6 在子代种群随机选择一个染色体生成其邻域解，按式（10）对两者进行选择，更新当前迭代次数g←g＋1；

步骤7 算法终止判定，若g≤Gmax，转步骤3循环计算，否则输出当前种群中最优染色体，并解码为最优运输路径方案．

3 算例分析

以我国某地区局部铁路网拓扑结构图为例，采用模拟OD车流数据，利用本文构建的优化模型进行配流和路径优化，验证模型及算法的适应性．

简化后的铁路网结构如图2所示，图2中有14个节点车站、23个路段．各流向超限货物量为：

1→13流向为82车；

1→14流向为94车；

12→13流向为103车；

12→14流向为97车．超限货物列车的平均编成辆数为K＝50，总载重4 000 t．超限货物装载后在直线与曲线上的轮廓分别为2 320和2 400 mm，属于超级超限情况．各路段的线路参数如表1所示．

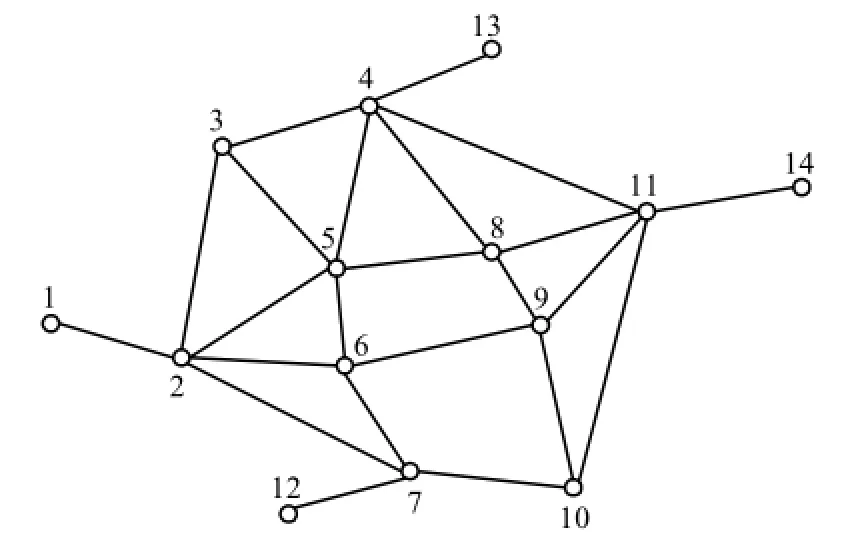
图2 铁路网示意图Fig．2 Schematic diagram of railway network

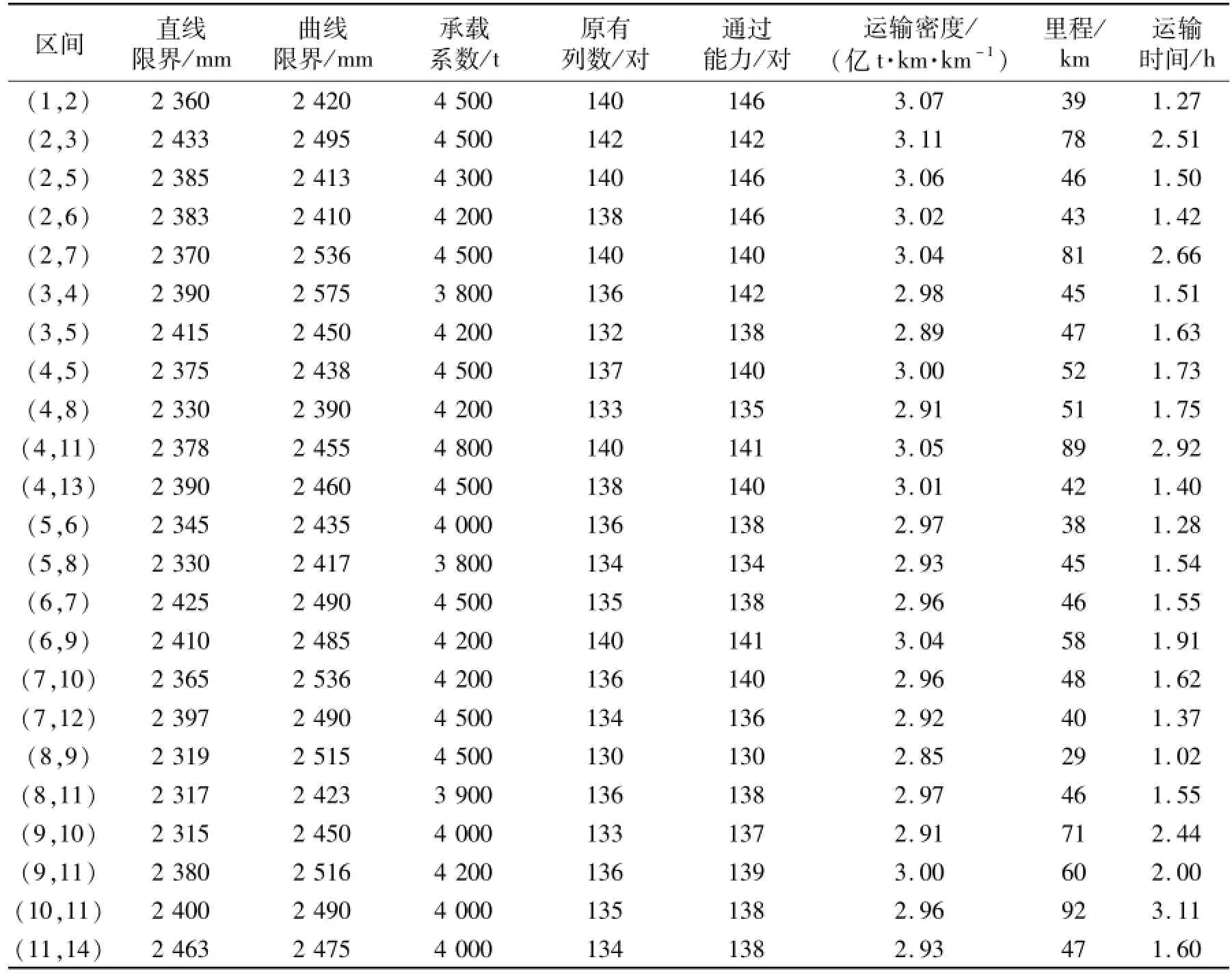
表1 各个路段的线路参数参考值Tab．1 Reference values of line parameters for different road sections

利用本文模型，经过试算和调整，最终确定各个参数值：种群大小为60，交叉概率

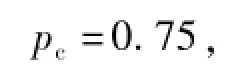
变异概率

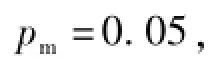
初始温度

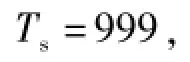
结束温度

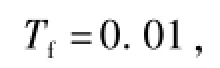
温度衰减参数

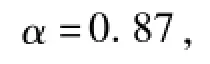
最大迭代次数

每次均包括算法对超限货物运输路径的寻优和对出发时间的调整．

当种群执行完选择、交叉、变异算子后，遗传操作停止，进入模拟退火Metropolics选择．整个计算求解过程基于Matlab7．0软件运行，最终得到目标函数最优的染色体为

解码后得到各流向超限货物的运输路径如表2所示．整个铁路网输送超限货物对正常运输组织的干扰程度为53．83，运输里程为871 km，运输时间为29．13 h．

表2 各流向路径选择结果Tab．2 Results of path selection in different flow directions

针对同一铁路网多流向超限货物运输路径优化问题，将本文方法与基本遗传算法和模拟退火算法的求解结果进行对比分析．在基本遗传算法的种群大小、迭代次数、编码、交叉与变异方式，以及模拟退火算法的温度衰减参数均与混合遗传算法相同的情况下，分别运行上述3种算法各6次，计算结果的对比如表3所示．

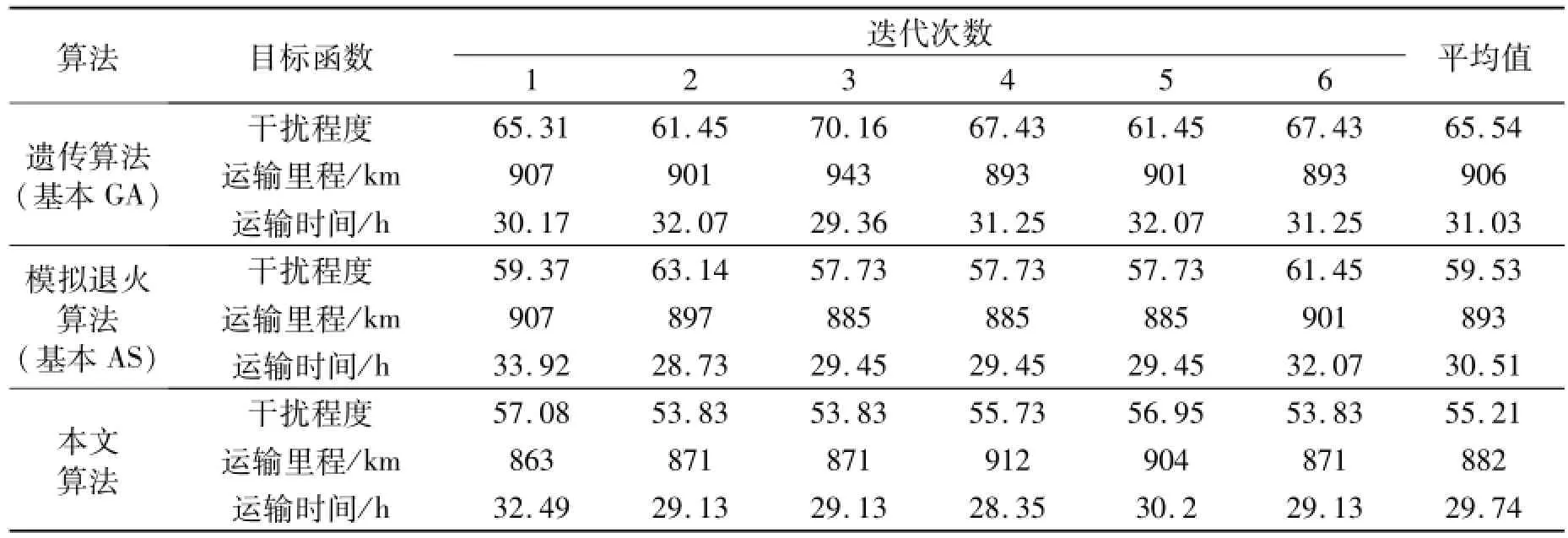
表3 仿真结果比较Tab．3 Comparison of simulation results

从表3可知，经过6次迭代后，本文设计的遗传模拟退火算法得到的3个目标平均结果优于遗传算法和模拟退火算法的平均结果，且在迭代过程中3次得到了该问题的最优解．可见，利用本文设计的改进遗传模拟退火算法，可以方便有效地求得多约束条件下的铁路网多流向超限货物运输径路优化问题的最优解或近似最优解．

4 结束语

作为超限超重货物运输调度的核心内容之一，路径方案的决策需要考虑其整体性与复杂性．本文综合考虑超限超重货物的运输里程、时间，以及对既有线路正常运营的干扰程度，在此基础上构建了多流向超限超重货物径路优化模型，用于确定不同流向超限货物的运输路径，并基于模型特点设计了遗传退火算法进行求解．通过14个节点车站、23个路段构造的铁路网算例，以及大量的仿真试验计算，获得以下结论：

（1）在该算法的设计和实现方面，采用组合序列编码方法产生初始种群，通过对交叉、变异等遗传算子的适应性设计，保证每个染色体的可行性，通过引入模拟退火策略，克服了不成熟的收敛，并增加了算法的邻域搜索能力．

（2）在算法性能方面，以某地区局部铁路网为例，分别采用遗传算法、模拟退火算法和遗传退火算法进行求解，通过对径路选择结果对比分析发现，遗传退火算法具有更好的全局寻优能力，同时验证了本文提出的遗传模拟算法在求解超限货物运输径路优化问题的优越性，具有重要的理论和现实意义．

［1］ 王花兰，李伟，张婷．铁路阔大货物装载加固方案比选方法的研究［J］．兰州铁道学报，2002，21（6）：112-115．WANG Hualan，LI Wei，ZHANG Ting．Study on the method of making choices from railway long heavy goods' loading and firming schemes［J］．Journal of Lanzhou Railway University，2002，21（6）：112-115．

［2］ 钟喜云．阔大货物装载加固方案评价［D］．成都：西南交通大学，2009．

［3］ 雷定猷．货物装运优化理论与应用研究［D］．长沙：中南大学，2005．

［4］ 汤波．铁路超限超重货物运输优化研究［D］．长沙：中南大学，2012．

［5］ 汤波．铁路超限超重货物运输径路综合优化模型与算法［J］．计算机应用研究，2012，29（8）：2876-2881．TANG Bo．Integrated optimizing model and algorithms of transportation route in out-of-gauge and overweight freights of railway［J］．Application Research of Computers，2012，29（8）：2876-2881．

［6］ 王新宇．铁路超限车运行组织优化研究［D］．长沙：中南大学，2012．

［7］ 尹晔飞．超限超重货物运输方案研究［D］．长沙：中南大学，2009．

［8］ 徐盛，雷定猷，张英贵．超限超重货物运输路径决策模型和算法［J］．铁道货运，2009（8）：31-35．XU Sheng，LEI Dingyou，ZHANG Yinggui．The model and algorithm of route decision in out-of-gauge and enhanced-load freight transportation［J］．Railway Freight Transport，2009（8）：31-35．

［9］ 任传祥，张海，范跃祖．混合遗传-模拟退火算法在公交智能调度中的应用［J］．系统仿真学报，2005，17（9）：2075-2078．REN Chuanxiang，ZHANG Hai，FAN Yuezu．Optimizing dispatching of public transit vehicle［J］．Journal of System Simulation，2005，17（9）：2075-2078．

［10］ 程博，杨育，刘爱军，等．基于遗传模拟退火算法的大件公路运输路径选择优化［J］．计算机集成制造系统，2013，19（4）：779-787．CHENG Bo，YANG Yu，LIU Aijun，et al．Highway transportation route selection optimization based on improved genetic annealing algorithm［J］．Computer Integrated Manufacturing Systems，2013，19（4）：779-787．

［11］ 蒋卓强．基于遗传模拟退火算法的静态路径规划研究［D］．重庆：重庆大学，2007．

［12］ 张东杰，牛瑶婷．铁路超限货物运输可行径路选择［J］．铁道运营技术，2010，16（3）：53-55．ZHANG Dongjie，NIU Yaoting．Railway out-of-gauge goods transportation behavior way choice［J］．Railway Operation Technology，2010，16（3）：53-55．

［13］ 刘胜，朱晓宁．超限车合理径路的选择方法研究［J］．物流技术，2011，30（6）：139-143．LIU Sheng，ZHU Xiaoning．Study on route selection for out-of-gauge trains［J］．Logistics Technology，2011，30（6）：139-143．

［14］ 王海星，海涛，李振江．铁路危险货物运输径路的选择策略［J］．北京交通大学学报，2009，33（6）：27-30．WANG Haixing，HAI Tao，LI Zhenjiang．Pathway selection process of dangerous goods railway transportation［J］．Journal of Beijing Jiaotong University，2009，33（6）：27-30．

（中文编辑：秦萍玲 英文编辑：兰俊思）

Routing Optimization Model and Algorithm for Out-of-Gauge Freights in Multiple Flow Railway Network

CHEN Hao1，2， WANG Wenxian1， LI Xueqin1
（1．School of Transportation and Logistics，Southwest Jiaotong University，Chengdu 610031，China；2．National United Engineering Laboratory of Integrated and Intelligent Transportation，Chengdu 610031，China）

In order to distribute the out-of-gauge freights reasonably to paths in railway network，a multi-objective optimization model was built for route selection of multi-direction out-of-gauge freights．In the model，the minimum transport route mileage，the minimum haulage time，and the minimum interference to the normal operation of the existing railway lines were taken as targets；and the distance between railway out-of-gauge freights and structure gauge，the railway transport capacity，and the loading capacity of the bridge along the way were used as constraints．According to the model characteristics，a multi-objective hybrid genetic algorithm was proposed to solve the model．In the algorithm，the natural array coding mode，together with cross and mutation operators，were designed to fit the constraints，and a simulated annealing strategy was introduced to enhance its neighborhood search capability．In addition，the proposed method was applied to the complex network containing 14 node stations and 23 sections to verify its validity．The application results show that the objective function values obtained by the proposed model and algorithm are superior to those obtained by genetic algorithm and annealing algorithm．Therefore，this method provides a technical measure for the decision-making of path selection in out-of-gauge freights transportation．

U294．6

A

0258-2724（2016）01-0145-07

10．3969／j．issn．0258-2724．2016．01．021

2014-09-27

中国铁路总公司重点资助项目（2014S14022）

陈皓（1986—），男，博士研究生，研究方向为运输组织优化理论与方法，电话：13568953471，E-mail：490646541＠qq．com

陈皓，王文宪，李雪芹．铁路网多流向超限货物运输路径优化模型及算法［J］．西南交通大学学报，2016，51（1）：145-151．