混合小波去噪在瞬变电磁资料处理中的应用
解海军, 颜 羽, 董 毅
(西安科技大学 地质与环境学院, 西安 710054)
混合小波去噪在瞬变电磁资料处理中的应用
解海军, 颜 羽, 董 毅
(西安科技大学 地质与环境学院, 西安 710054)
为提高小波阈值去噪在瞬变电磁资料处理中的效果,将多种改进的小波阈值函数和传统小波阈值函数对各实测TEM数据进行滤波处理,再按一定的标准筛选出各点最优的阈值处理函数作为该点最终的去噪函数。结果表明:对比混合小波和单一小波函数去噪的效果发现,混合小波去噪在瞬变电磁资料处理中能更有效压制噪声,突出信号异常,去噪效果优于单一的阈值去噪方法。通过改进该混合小波函数去噪的代码还可以筛选出适合各点去噪的最优小波基,使混合小波去噪更加完善。
瞬变电磁; 混合小波; 小波去噪; 阈值函数
0 引 言
野外瞬变电磁在数据采集时,经常受到高压线、厂矿影响等各种人为因素的干扰,导致噪声掺杂在信号源中,使采集数据的质量受到一定程度影响,给地质异常特征的分析与解释带来诸多不便。小波去噪通过在时频领域对原始信号进行多尺度分解,利用阈值去噪后再对信号重构,可在压制噪声的同时,有效保留有用信号。近些年来,小波去噪在瞬变电磁资料的处理中应用较多,将小波变换用于瞬变电磁去噪中,有效提高了信噪比,取得较好的去噪效果[1-3]。但传统的小波软、硬阈值去噪是将分解出的噪声系数按照某一固定值衰减或直接置为零,这会导致去噪前后小波系数间存在恒定的偏差。因此,一些学者对阈值函数进行改进,许文博[4]和张弛等[5]通过构造出新的阈值去噪函数,再经仿真实验证明其去噪效果优于传统的小波去噪。
上述对小波阈值函数改进后其相较于软、硬阈值去噪效果有了明显改善,但均为单一的阈值函数去噪方法,而同一种阈值函数可能只对个别测点的去噪效果很好,却不一定适合于研究区的所有测点[6-8]。鉴于此,笔者利用混合小波阈值函数对瞬变电磁数据进行去噪,通过将多种小波阈值函数同时对某测点去噪,并计算出各个阈值函数的信噪比及最小均方差。信噪比越大,表明有用信号越强,最小均方差越小,表明测点的衰减曲线越光滑,数据质量越高[9]。为在提高信噪比的同时保证数据质量,需要综合考虑这两个因素。对同一点同时对比两个判别标准较为困难,因此,文中利用判别标准MS值,针对各个测点筛选出其最优的阈值去噪函数,然后分别对所有测点进行混合去噪,并结合实例,对混合小波去噪后的效果进行评价。
1 单一的小波阈值函数去噪
小波阈值去噪认为,信号经小波变换后,能量不同的信号可转化为值大小不同的小波系数,有效信号的能量集中在小波域内的有限几个系数中,而噪声系数能量分布在整个小波域内[10],经小波分解后有用信号的小波系数要大于噪声信号。因此,设置合适的阈值,尽可能剔除噪声保留有用信号的小波系数,再经逆小波变换重构新的小波系数,就可达到去噪的目的。小波阈值去噪的核心是小波阈值的处理。1.1 传统的小波阈值函数去噪
传统的小波去噪函数包括硬阈值去噪和软阈值去噪,它们的去噪函数如下[11-12]:

(1)
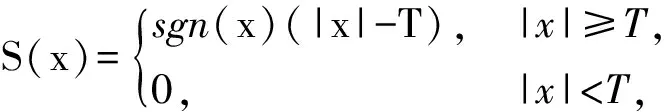
(2)
其中,式(1)为硬阈值去噪函数,式(2)为软阈值去噪函数。对实例数据进行硬阈值去噪处理时发现,部分点因硬阈值函数的不连续性而出现较大奇异值,因此,不作硬阈值去噪效果的进一步研究,只对比软阈值去噪和改进阈值去噪的效果。
1.2 改进的小波阈值函数去噪
改进的小波阈值去噪函数较多,文中为了体现混合小波去噪的效果,另外选用了两种改进的小波去噪函数,定义如下:
(3)
(4)α、β为调节参数,取值范围为0~1,通过改变α、β值的大小,改进的阈值函数可在软硬阈值函数之间变动,其中函数αT-βT/[1+exp(x/T)]可使原始采集的数据,经分解后计算出的绝对值大的小波系数作变动衰减,有效减小高频信息的损失,且具有很大的灵活性。张晓宁[13]对此阈值函数做了大量仿真实验,证明当α=0.4,β=0.618时,去噪效果最好。
2 混合小波阈值去噪
混合小波去噪是综合HY和HD阈值去噪函数和软阈值函数,通过Matlab编程自动筛选出各测点最优去噪函数,最后对所有测点依次进行混合滤波。衡量信号去噪效果好差的标准为均方误差(Eu)及信噪比(γ)[14]。其定义如下:
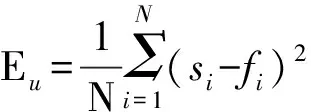
(5)
(6)
式中,si是原始信号;fi为小波阈值处理后的信号;N为信号长度。为筛选出各测点最优的阈值去噪函数,定义新的去噪效果判别标准σ:
σ=γ/100+Eu。
(7)
它综合考虑了信噪比和均方误差,能够在提高有用信号强度的同时提高信号质量,其中σ越小,信号去噪效果越好。
3 混合小波去噪应用实例
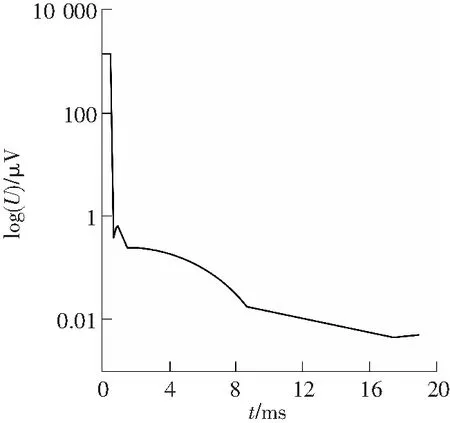
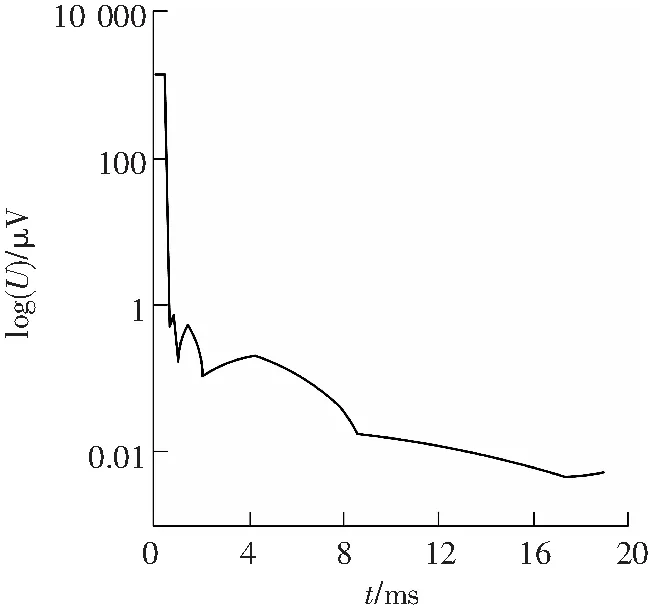
陕北张家峁煤矿是一座大型的现代化矿井,矿区烧变岩分布较广,由于安全生产的需要,需对矿区烧变岩的富水性分布情况进行探查。综合考虑已知地质资料和勘探区情况,施工时采用对低阻反应敏感、施工效率高的瞬变电磁法。工作时使用TerrTEM中功率瞬变电磁仪,数据采集延迟时间为20ms,78道时间窗口,保证了每个测点在不同深度上具有足够的采样数据。由于矿区高压线纵横遍布,人文干扰较强,仪器中自带的滤波方法未能有效压制干扰,衰减曲线出现一定的波动,数据的质量不够理想。数据处理时采用混合小波去噪方法,小波基的选择对除噪效果有一定的影响,数据处理中经过多次对比,发现bior2.4小波的降噪效果明显好于其他小波,信噪比和均方误差都较小,因此,选择bior2.4小波作为去噪小波基。首先,对原始信号进行小波分解,再进行阈值去噪,然后,对分解后的小波系数进行合成、重构信号,得到去噪后的瞬变电磁信号。对于阈值的选取,采用Matlab中的自适应阈值函数获得。为更清晰对比各种小波函数的去噪效果,图1中分别绘出各个去噪函数降噪后的衰减曲线,图1和图2是测线上7号点和20号点的三种阈值函数去噪后的衰减曲线。
从滤波后的曲线可以明显看出,对于7号点HY的去噪效果要优于其他函数,对于20号点HD的去噪效果最优。混合小波去噪会自动对于7号点选用 函数去噪,20号点选用HO函数去噪,图1和图2也说明了混合小波去噪用σ值作为筛选最优去噪函数是有效的。表1列出前10号点的σ值及第20号点的σ值。
图3是受干扰严重的一条勘探线所采集的原始数据经计算、反演、绘制的拟视电阻率断面。图3a中可以看出,地层的分层性较好,低阻异常体位置明显。但由于噪声的干扰,导致异常分布较多,影响物探资料的地质解释精度。图3b是经混合去噪后的数据绘制的拟视电阻率断面,可以看出,经去噪后异常体的分布并未改变,但由噪声引起的异常得到有效的压制与消除,突出了局部异常特征,结合地质资料能够有效提高异常解释的准确性。

a 实测衰减曲线
b HY阈值函数去噪

c HD阈值函数去噪
d 软阈值函数去噪

a 实测衰减曲线
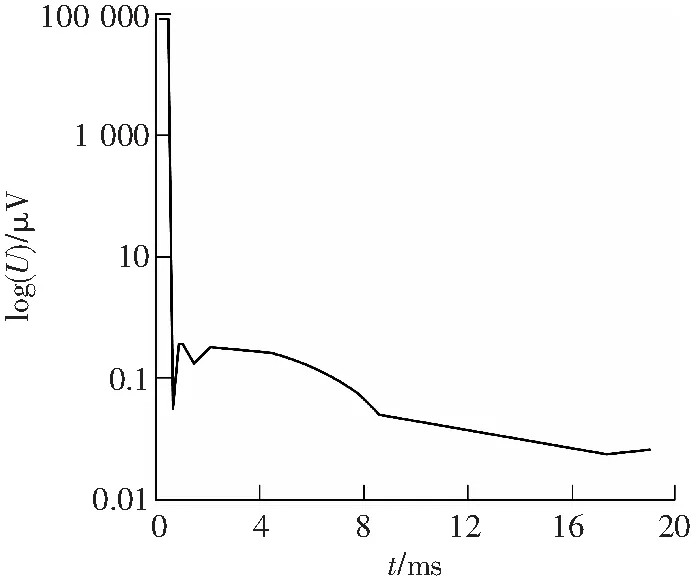
b HY阈值函数去噪
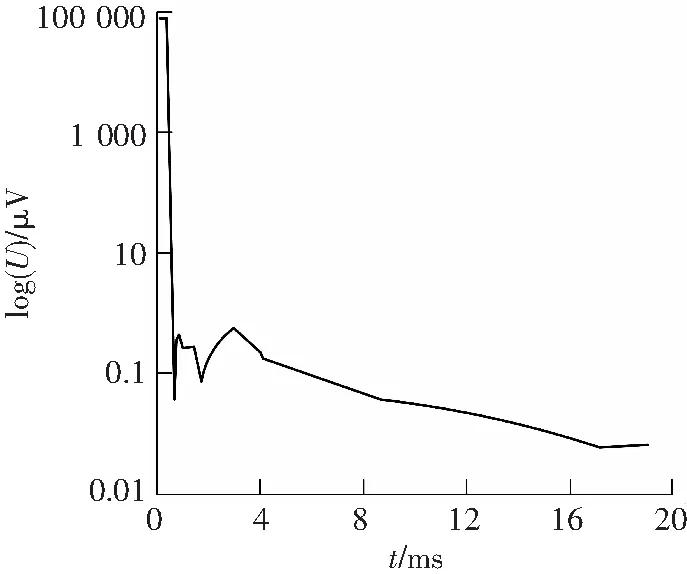
c HD阈值函数去噪
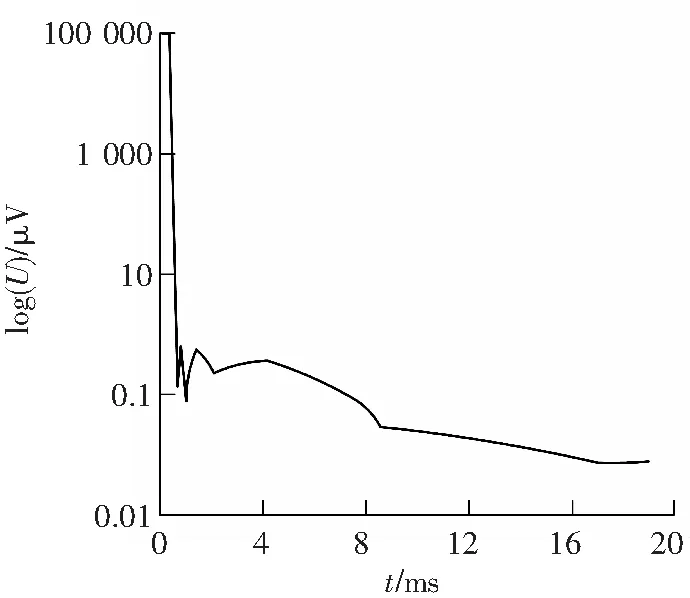
d 软阈值函数去噪
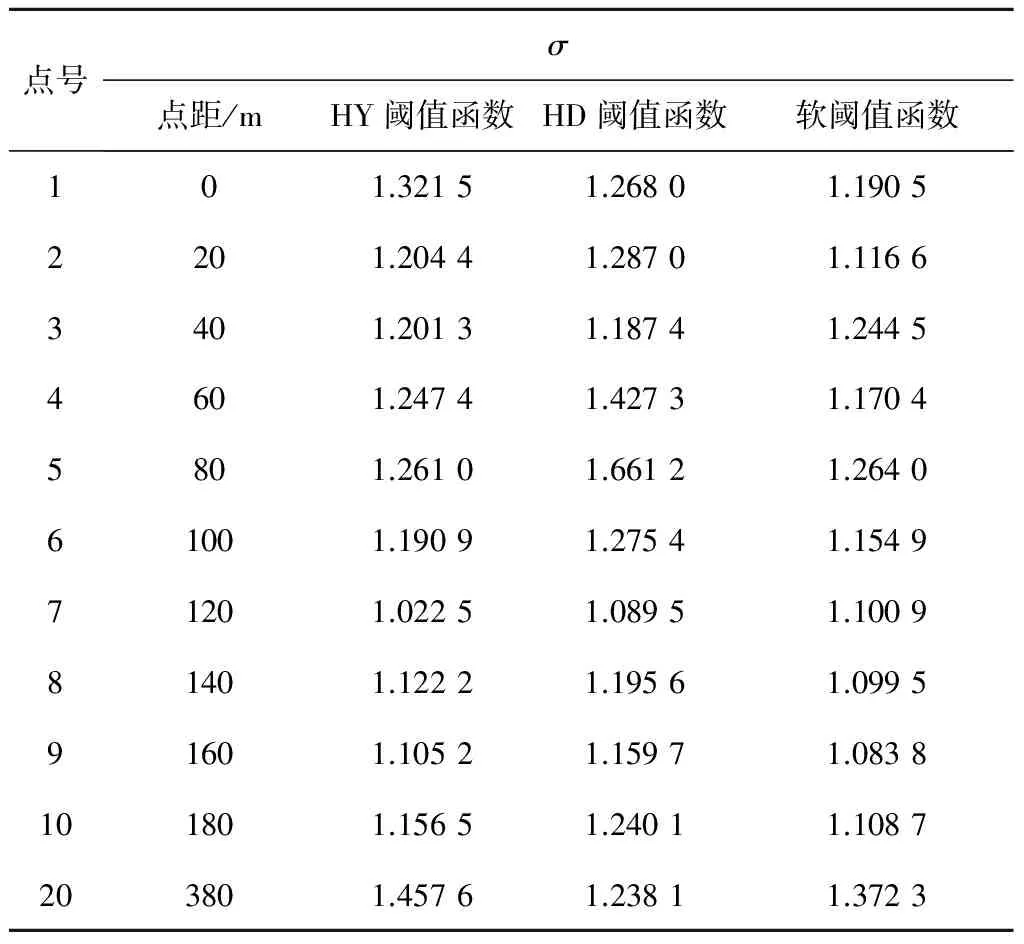
表1 三种小波去噪阈值函数的σ值对比
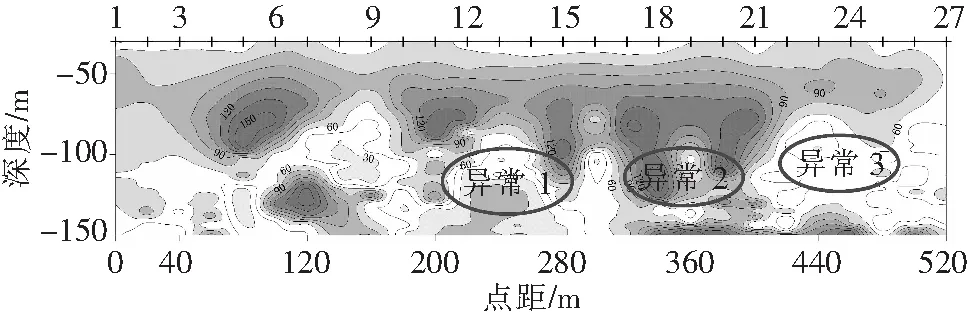
a 去噪前
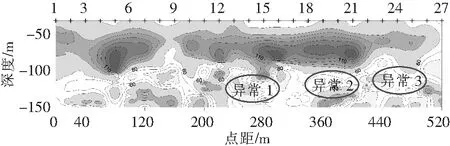
b 混合小波去噪后
4 结 论
将混合小波去噪应用于瞬变电磁资料的处理中,经分析对比去噪的效果,得出以下结论:
(1)混合小波去噪通过对比σ值筛选出各测点最优的去噪函数,既消除了传统的阈值去噪函数时存在的恒定偏差的缺陷,也避免了用单一的阈值函数对所有测点进行去噪。可以优化小波阈值去噪的效果,提高地质资料解释的准确性。
(2)混合小波去噪中可以通过添加合理改进的小波阈值函数提高去噪效果,灵活性很大。
(3)小波去噪的效果还与小波基的选取有关,混合小波中在对阈值函数对比筛选的同时,也能够筛选出各测点最优的小波基,可使混合小波阈值去噪更加完善。
[1] 闫 赛, 郭恒庆, 刘树才, 等. 小波变换在瞬变电磁数据去噪中的应用[J]. 工程地球物理学报, 2010, 7(6): 656-660.
[2] 解海军, 曾方禄, 姬中奎. 基于小波分析的瞬变电磁法资料去噪技术[J]. 煤炭学报, 2006
[3] 解海军, 孟小红, 王信文, 等. 煤矿积水采空区瞬变电磁法探测的附加效应[J]. 煤田地质与勘探, 2009(2): 71-74.
[4] 许文博, 武晓春, 邢建平. 一种新的小波阈值去噪方法[J]. 兰州交通大学学报, 2012, 31(3): 120-124.
[5] 张 驰, 李 翔, 姚 磊. 一种改进的小波阈值函数去噪方法[J]. 计算机与现代化, 2014(3): 219-222.
[6] 崔国华. 小波变换在煤层自燃区瞬变电磁数据去噪中的应用[J]. 煤炭与化工, 2014(7): 40-42.
[7] 程文波, 陈劲松. 一种新的改进阈值的小波包图像去噪方法[J]. 西安科技大学学报, 2010, 30(4): 479-483.
[8] 刘家富, 雷 宛, 张 扬, 等. 瞬变电磁信号去噪方法对比分析与评价[J]. 工程勘察, 2014(11): 88-93.
[9] ZHOU MAX C, KEN PIJ. Interpretation of wavelet analysisand its application in partial discharge deteertion[J]. IEEE Trans.on Dielectrics Ricsand Electrical Insulation, 2002, 9(3): 446-457.
[10] 李蕴奇. 基于小波变换的图像阈值去噪及其效果评估[J]. 东北师大学报: 自然科学版, 2012, 44(1): 60-66.
[11] 刘家富, 雷 宛, 张 扬, 等. 基于改进的小波阀值的瞬变电磁去噪应用研究[J]. 工程地球物理学报, 2014(4): 547-552.[12] 沈显庆, 段小龙. 变电站容性设备介损在线监测数据压缩与预处理方法[J]. 黑龙江科技大学学报, 2016, 26(2): 187-191.[13] 张晓宁, 孙丽君. 一种改进的小波阈值信号去噪方法[J]. 电子科技, 2012(11): 15-17.
[14] 刘卫东, 刘尚合, 胡晓峰, 等. 小波阈值去噪函数的改进方法分析[J]. 高电压技术, 2007(10): 59-63.
(编辑 晁晓筠 校对 李德根)
Application of mixed wavelet denoising method in TEM data processing
XieHaijun,YanYu,DongYi
(College of Geology & Environment, Xi’an University of Science & Technology, Xi’an 710054, China)
This paper is an effort to improve the effect of wavelet threshold denoising on transient electromagnetic data processing. The effort is directed at applying a variety of improved wavelet threshold functions and the traditional wavelet threshold functions for filtering all the measured TEM data; and according to a certain criterion, selecting the best optimal threshold function of each point as the final denoising function. The comparison between the denoising effect of mixed wavelet and that of single improved wavelet reveals that, when applied in transient electromagnetic data processing, the mixed wavelet method may afford a better denoising effect than the single threshold denoising one, thanks to its more effective noise suppression and better abnormal signal clarification. An improvement in the mixed wavelet denoising function allows the selection of the optimal wavelet base suitable for each point, thus contributing to a better performance of the mixed wavelet denoising method.
TEM; mixed wavelet; wavelet denoising; threshold functions
2016-10-16
西安科技大学科研培育基金项目(2015QDJ082)
解海军(1969-),男,陕西省兴平人,副教授,博士,研究方向:电法勘探技术,Email:xhj_ccri@163.com。
10.3969/j.issn.2095-7262.2016.06.020
P631.3
2095-7262(2016)06-0687-04
:A

