流域水污染治理动态模糊参与度模型研究
唐红霞
(辽宁省丹东水文局,辽宁 丹东 118001)
流域水污染治理动态模糊参与度模型研究
唐红霞
(辽宁省丹东水文局,辽宁 丹东 118001)
生态文明的构件取决于流域水资源和水环境的条件改善。流域是完整性比较高的生态体系,流域在不同区域的关联性很强,要想处理水污染问题就需要各个区域相互配合工作才能完成。在此期间就需要把进行污染处理所需的成本就需要各方进行资金的合理分配。对进行水污染处理中所产生的利润分配构建水污染动态治理模糊参与度模型,利用动态夏普利值进行模型准确度的验证。
模糊参与度;动态夏普利值;水污染;利润分配
0 前 言
我国大部分领土都是流域,其中有无数条小河流,横穿于不同的流域区域,流域的污染问题影响着国家经济的快速发展,流域水资源的保护和水资源环境条件的改善对对河流污染的治理起着决定性的作用。国内外相关学者主要是针对夏普利值的理论研究,更多的是放在静态上的理论研究,对动态的研究困乏[1-3]。
对水污染治理的动态模型的建立是时代发展的必然趋势,本文通过建立动态模糊参与度模型,把模型应用到具体工程案例中。
1 夏普利值在流域水污染治理利润分配中的应用
1.1 基本假设
选取相邻的三个区域进行分析,设定集合N={1,2},1表示上游区域,2表示中游区域。对这两个区域进行联盟为两种形式:①区域之间不结合而成的单独联盟{1}、{2};②两个区域相互配合而成的强强联盟:{1,2}。博弈持续期间的集合为Γ=[0,T]。
假设1令Qi(t)表示区域i在时刻t的工业生产量,所排放的污染量为ei(t),如果设工业生产量与污染排放产量成正比,即Qi=Qi(ei(t))。区域i利用工业生产所取得的利益为Ri(Qi),因此,对应的利益ei(t)的表达式为:

0≤ei(t)≤bi
(1)
式中:bi为给定系数,代表利润最大时的排放量。
假设2:区域i项目成本ci与投资金额hi的关系是逐渐增加的二次凸函数,即:
(2)
式中:ai为投资成本效率系数。
假设3:工业所排放的污染物给流域所产生的成本破坏di(s)受至于流域各区域的污染存放量k,即:
di(s)=πiki(t),πi>0
(3)
式中:π为污染物对区域i的破坏程度。
假设4:区域i利用投资项目降低的污染减排量ERUi(t),令其和投资hi成线性关系,即:
ERUi(t)=rihi(t),ri>0
(4)
式中:ri为投资规模参数。
1.2 模型构建
1.2.1 区域间不结合
区域i在标准时间内取得的利润大小:
(5)
ki(t)的辩护主要受新增的污染排放量、治理降低的污染排放量、污染物的自然衰减量的影响,可以通过下述方程为:
ki(t)=ei(t)-rihi(t)-δiki(t)-φiki(t)
(6)
式中:δ为对污染物的吸收率(0<δ<1)。
利用贝尔曼的动态计划,可以分析:
-Vt(0)i(t,ki)=max
(7)
对上式进行求导并取最大值,为:
ei0*(t)=bi+Vki(0)i(t,si)e-rt,hi0*(t)
(8)
区域i在要求时间内所取得的利润函数是:
V(0)(t,ki)=e-rt[Ai(t)ki+Bi(t)]
(9)
把(9)式带到(8)式中,可以得出:
ei(0)*(t)=bi+Ai(t)
(10)
1.2.2 强强联盟
两个区域进行强强联盟所取得的利润为:
-π12k12(t)]e-rtdt
(11)
两区域所排放的污染量公式表达式为:
(12)
利用贝尔曼的动态计划,进而有:
-Vt(0)12(t,k12)=max
(13)
其求导来算最大值,最大值的条件为:
e120*(t)=b12+Vk12(0)12(t,k12)e-rt,
(14)
在时间要求范围内所取得的利润表达式为:
V(0)12(t,s12)=e-rt[A12(t)s12+B12(t)]
(15)
将(15)带进(14),可以求得:
e1(0)*(t)=2bi+2A12(t)
e2(0)*(t)=2b2+2A12(t)
(16)
2 算例分析
2.1 选取参数
进行区域的选取,要求选择两个区域的发展状况相差大,治理措施不一样的区域[4-6]。取所选取的区域所涉及到的参数值为:
a1=0.5,a2=1,a12=1.5,b1=20,b2=40,h1(1)=h1(2)=10,h2(1)=h2(2)=20,e1(1)=20, e1(1)=30,e2(1)=30 , A1(1)=-6, B1(1)=20, A2(1)=-8, B2(1)=30, A12(1)=-14, B12(1)=50, A(1)=-24, B(1)=90,r1=0.5,r2=1,r12=1.5,π1=4,π2=5,π12=9,k11=20,k21=30,δ1=δ2=δ12=0.1,r=0.05。

表1 两区域在联盟过程中的参与度
2.2 计算结果
依靠上述参数度的大小,进而可以求出3个区域在不同联盟方式下的参数变化值,详细见表2、表3、表4。
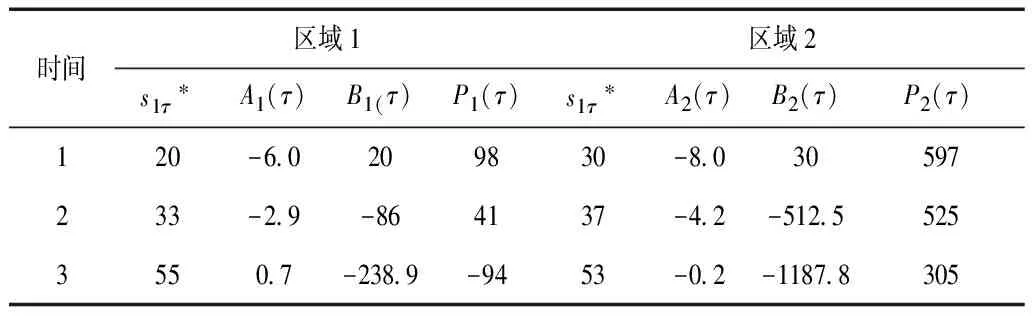
表2 区域间不结合下的参数值

表3 区域间合作下的参数值
对此,可以计算出区域1在时刻t=1时的利润。

表4 区域1在t=1时分配到的利润
根据上述计算方式,进而可以求出量区域合作的动态夏普利值,见表5所示。

表5 区域1和区域2在时间要求内的利润分配情况
通过表5中的数据分析可知:进行流域水污染的治理以后,对这两个区域的利润分配依据夏普利值进行得到如下结果:第1个区域的盈利开始为-807.38,进行治理后慢慢上升到307.30,第2个区域的利润值开始为-604.98,进行治理后逐步上升到1059.04,第1个地区的利润实现正侧增长是从治理的第3期开始的,第2个区域的利润实现正增长是从治理第2期开始的[7]。
3 结 语
本文主要是通过把模糊联盟与动态夏普利值方式相互结合,将流域的水污染治理过程中的获利情况进行分析,在分析过程中主要参考2个方面的情况:
1)参加联盟的区域数量不确定性。
2)对于流域的水污染情况进行治理是一个长期的过程,由于这个过程中存在许多的不确定因素,所以也是一个动态的过程。
考虑到以上现两点,本文的分析结果可为流域的水污染治理提供一个可靠度高的参考依据。
[1]李学森.凌河流域水资源现状及保护措施[J].水土保持应用技术,2015(03):36-37.
[2]高素丽.辽阳市水资源开发利用和管理保护对策[J].水土保持应用技术,2011(04):45-47.
[3]柴雅丽,霍延召.朝阳市水资源供需矛盾分析及解决途径[J].水土保持应用技术,2015(03):44-45.
[4]凌敏华,陈喜,程勤波,等.地表水与地下水耦合模型研究进展[J].水利水电科技进展,2010(04):79-84.
[5]包宇.大凌河流域朝阳区段水环境恢复治理对策[J].水土保持应用技术,2011(06):39-40.
[6]郭福厚,梁凤国.辽宁省湿地资源保护的对策分析[J].水土保持应用技术,2006(01):33-34.
[7]郎俊,孙晓菊,朱茂森.抚顺市构建节水型社会的必要性及措施[J].水土保持应用技术,2012(05):29-30.
1007-7596(2016)11-0031-03
2016-11-02
唐红霞(1981-),女,辽宁丹东人,工程师,研究方向为水资源管理、水资源开发利用、水质监测等。
X522
B

