混沌蚁群算法应用于小规模换热网络综合问题

张春伟，崔国民

（上海理工大学 新能源科学与工程研究所，上海 200093）

混沌蚁群算法应用于小规模换热网络综合问题

张春伟，崔国民

（上海理工大学 新能源科学与工程研究所，上海 200093）

针对换热网络综合问题的严重非凸、非线性，采用一种混沌优化算法即混沌蚁群算法，同步综合换热网络。为充分验证混沌蚁群算法的搜索能力与特性，选择相对于固定结构更为复杂的小规模换热网络综合问题作为研究对象。同时引入Powell法作为局部搜索策略，提高算法的求解精度。选用3个小规模算例对算法进行验证，均获得了相对文献更好的换热网络设计，证明了混沌蚁群算法优越的搜索能力。

换热网络综合；混沌蚁群算法；Powell法

换热网络同步综合的目的是发现一个年综合费用最小的网络结构，其研究方法大致可分为确定性方法和随机性方法两类。确定性方法以分支定界法［1］和外部逼近法［2］等为代表，但其在处理大规模换热网络问题时存在一定的不足。随机性方法，如遗传算法［3］、微分进化算法［4］和粒子群算法［5］等，已在换热网络中得到广泛的应用。但此类算法受种群多样性等因素影响，易陷入局部最优解。

混沌优化算法是一类基于混沌动力学的新型优化方法，如混沌神经网络算法［6］、混沌模拟退火算法［7］和混沌免疫算法［8］等，得到了学者们的广泛研究。混沌特有的遍历性、伪随机性等使混沌优化算法具有很强的爬山及跳出局部最优能力，所以混沌搜索较随机搜索更加有效。混沌蚁群算法是一种基于混沌理论和自组织理论的新型混沌优化算法［9］，已成功解决参数辨识［10］、电力资源分配［11］和多目标优化［12］等问题，具有搜索能力强、性能稳定等特点。

本工作将混沌蚁群算法应用于小规模换热网络问题，分析算法的搜索能力与特性，并提出了一条能够适用于混沌蚁群算法的判断准则，辅助算法处理问题中的整型变量，同时引入Powell法作为局部搜索策略，提高混沌蚁群算法的求解精度及搜索能力；选用3个算例对算法进行了验证。

1 换热网络综合问题的数学模型

1.1 超结构模型及其序列表示

换热网络综合问题可表述如下：有NC股冷流体需要加热，NH股热流体需要冷却，通过冷、热流体之间的匹配，回收过程流体的能量，同时为未达到目标温度的流体设置热、冷公用工程。冷、热流体的进口温度、目标温度、热容流率，公用工程的进、出口温度，各换热器换热系数等均已知。根据冷、热流体的匹配顺序形成一个换热网络，在所有流体达到目标温度的情况下，最小化换热网络的投资费用与运行费用。投资费用包括换热器固定投资费用与换热器面积费用，运行费用为公用工程消耗所产生的费用。对于有分流的换热网络模型而言，虽然有时能够得到相对无分流模型费用值更低的换热网络设计，但由于增加了问题的复杂性，且未计算由于流体分流而增加管路、阀门等造成的额外投资费用，所以在实际工程中的可接受度不高。鉴于此，本工作采用Grossmann无分流分级超结构模型［13］，其中，换热网络级数为NS=max（NH，NC），最大换热器个数为NK=NSNHNC。以2股热流体与2股冷流体为例，分级超结构模型见图1。

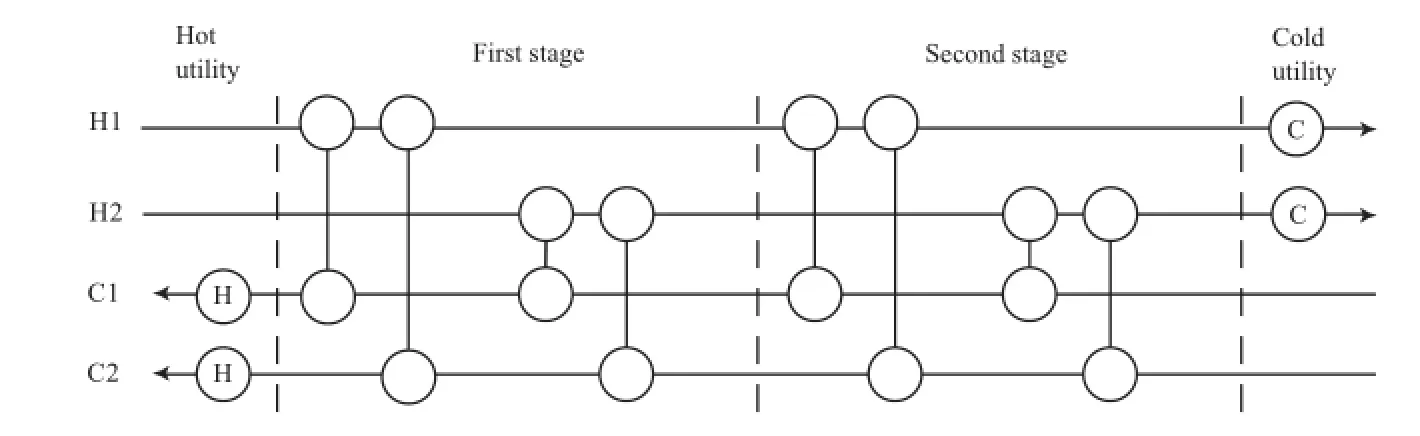
图1 换热网络无分流的分级超结构模型Fig.1 Superstructure of heat exchanger networks without stream splits.H1，H2：hot fuids；C1，C2：cold fuids.

1.2 优化的目标函数

针对上述换热网络模型，以最小年综合费用为优化目标，其数学函数为：

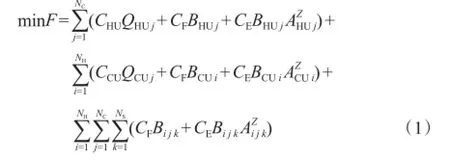
式中，当换热器存在时，B=1；反之，B=0。

本工作以单个换热器的换热量Qijk为优化变量，各换热器均采用逆流传热方式。换热器相关参数的计算式见式（2）～（4），加热器与冷却器的计算方式与换热器相同。

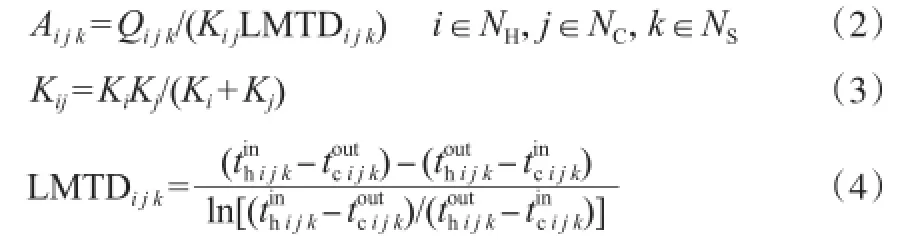
当进行匹配的冷、热流体的热容流率相等时，可采用算术平均温差AMTD代替对数平均温差LMTD，AMTD的计算式见式（5）。具体约束条件见文献［14］。

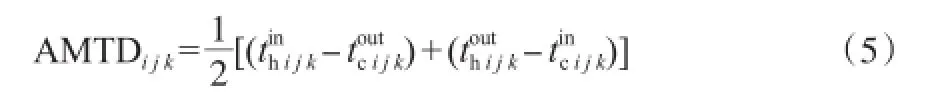
2 混沌蚁群算法

2.1 混沌蚁群算法

混沌蚁群算法中的搜索过程中包含两个连续阶段，即蚂蚁个体的混沌搜索阶段和整个种群的自组织阶段。单个蚂蚁的混沌行为到整个种群自组织行为的转变是通过引入一个连续改变的组织变量来实现的。为使蚂蚁个体在开始时进行混沌搜索，文献［9］引入Solé等［15］给出的混沌函数并进行相应改进，得到变量更新公式（以种群Np中第n个蚂蚁，第G代更新为例），见式（6）：

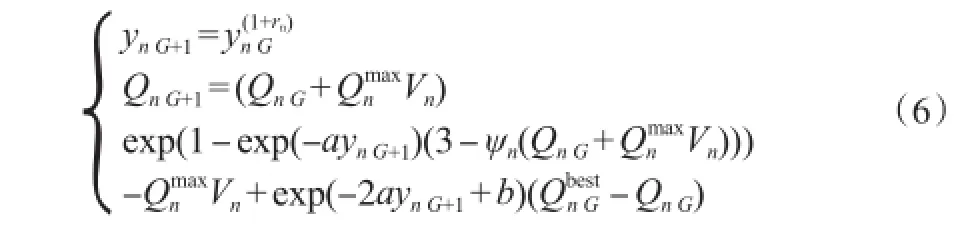
式中，为蚂蚁个体的搜索范围，其每一维大小为每个换热器所在冷热流体的最大换热潜能；为蚂蚁个体邻居反馈的最佳位置；Vn决定了蚂蚁个体在每一维空间上的搜索范围，如Vn=1/2，则表示此蚂蚁的混沌动力学行为方程的吸引子与Vn=0时相比，向负方向移动了一半，本工作令Vn=0.1；其余相关参数可参考文献［9］。

2.2 局部搜索策略

根据混沌搜索特性，蚂蚁会遍历整个求解域，但由于换热网络问题的非凸、非线性严重，对算法的精度要求高，所以引进Powell法作为局部搜索策略。蚂蚁每移动到一个新点，Powell法会找到其所在区域的局部最优值。在算法收敛阶段，蚂蚁会聚集在种群保存的最优解上。此外，由于蚂蚁个体具有记忆功能，局部搜索并不会影响蚂蚁的搜索路径。Powell法是一种求解无约束最优化问题的直接搜索法［16］，具有收敛速度快、求解精度高、无需计算导数等优点，较其他传统的局部优化方法更适合换热网络综合问题。Powell法搜索的步骤如下。

步骤1：确定变量维数N，即当前蚂蚁个体结构所包含的换热器个数，读取当前位置信息Q0。设置收敛精度ε。给定一组线性无关的方向De（e=1，2，…，N），De取N个坐标轴的方向，即N阶单位矩阵。其中N的最大取值为NK。

步骤2：从初始点Q0出发依次沿方向De（e=1，2，…，N）进行一维搜索，确定每次迭代的步长λe，得到Q1，Q2，…，QN，即：

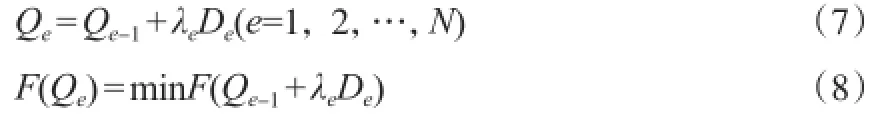
步骤3：判断迭代计算是否结束。若满足式（9），则得到解QN，计算结束；否则进行步骤4。

步骤4：计算最速上升方向上函数F（Q）的变化：

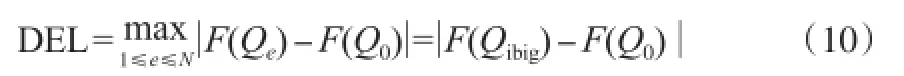
步骤5：引进第（N+1）个搜索方向和新的点Qt，并计算F（Qt）。

步骤6：方向替换判断。

若满足式（13），则将QNh作为新的初始点，沿原方向重新搜索，即转至步骤2。

若满足式（14），则将QN作为新的初始点，沿原方向搜索，即转至步骤2。

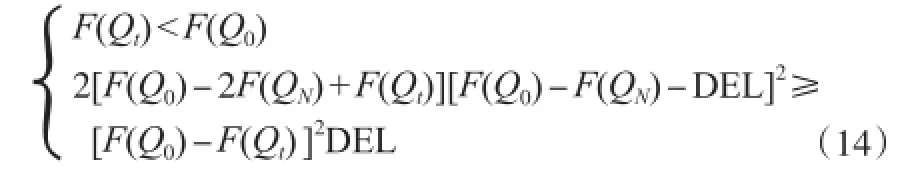
若以上两条件均不满足，则转至步骤7。

步骤7：以QN作为起始点，沿方向DN+1进行一维搜索，并得到此方向上的极小值点QN+1。将方向Dibig用新方向DNh+1=QN+1-QN替换，产生一组新的方向组De（e=1，2，…，N），以QN+1作为新初始点，转至步骤2。

2.3 整型变量判断准则

在本工作中，所有个体的初始解均为全结构，即所有换热器都存在。通过测试发现，混沌蚁群算法能够使个体的某一维的换热量Q近似为零。从投资费用方面分析，当某一换热器上的热负荷小于一特定值时，可认为此换热器对于减少年综合费用值是不利的，即这一维表示的换热器应该消去。但由于精度的影响，优化变量Q不可能完全为零。鉴于此，本工作提出了一条适用于混沌蚁群算法的整型变量判断准则，见式（15）：

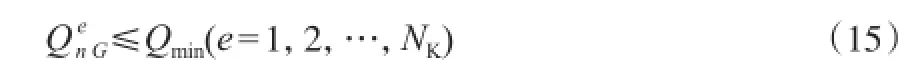
式中，Qmin为设定的换热器最小换热量，当蚂蚁个体某一维的变量小于此值时，消去对应的换热器。当换热器被消去后，若费用值降低，则此新解作为最佳的概率相应增大，种群中其他个体倾向于消去此换热器；若费用值升高，则此新解作为最佳的概率相应减小，所以其他个体消去此换热器的概率也相应减少，而此个体在下次迭代过程中又可通过学习其他个体，重生已消去的换热器。此外，由于混沌蚁群算法本身具有一定的跳出局部最优的能力，且本工作研究的对象均为小规模问题，所以判断准则对整型变量具有一定的处理能力，但并不适用于大规模换热网络问题。

3 算例验证

为验证混沌蚁群算法算法性能，本工作选取3个小规模算例进行计算。计算环境为WIN7系统下Fortran编程，计算机参数为Intel（R） Xeon（R） CPU E5-2670 v2 2.5 GHz 32 GB RAM。

3.1 算例1

算例1取自文献［17］，相关参数见表1。采用基于局部搜索策略的混沌蚁群算法优化算例1，优化结构见图2，计算所得费用值为115 890 $/a。算例1混沌蚁群算法的计算值与文献方法计算结果的比较见表2。严丽娣等［17］采用标准粒子群算法优化算例1，获得结构对应的费用值为124 670 $/a，但未直接说明如何处理整型变量。何巧乐［18］提出了具有局部搜索能力的文化基因粒子群算法并采用一种处理策略避免由于固定投资费用较高引起算法陷入局部最优解，将其应用于算例1后，所得结构的费用值为123 900 $/a。

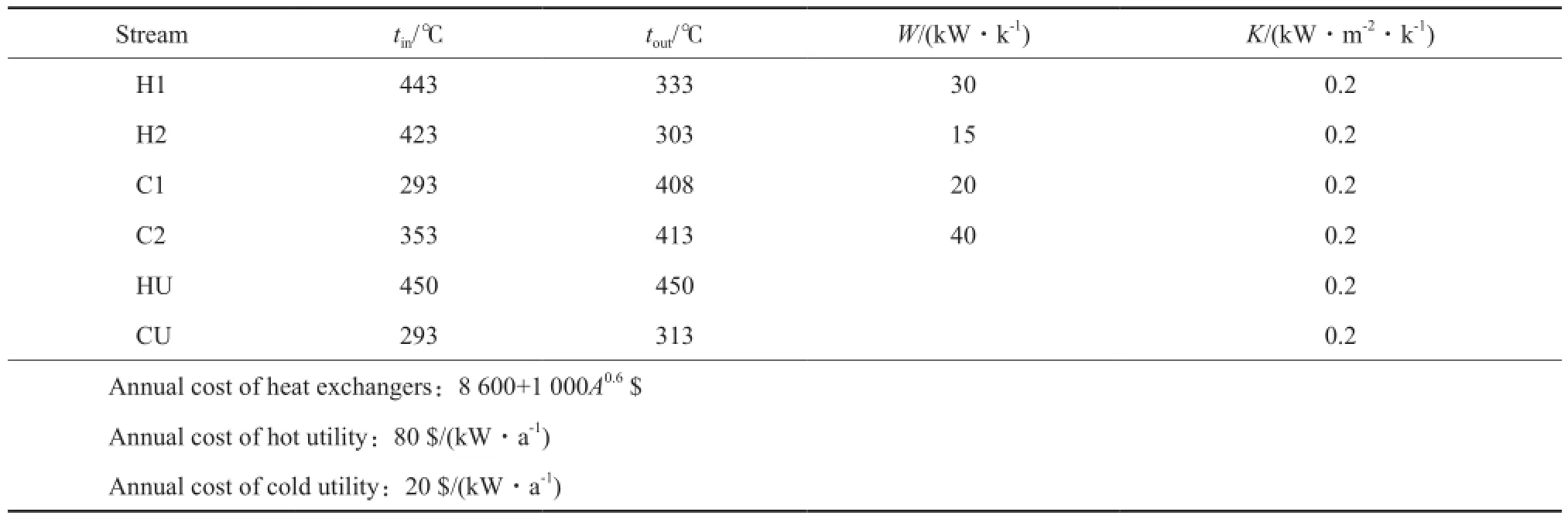
表1 算例1的参数Table 1 Parameters of case 1

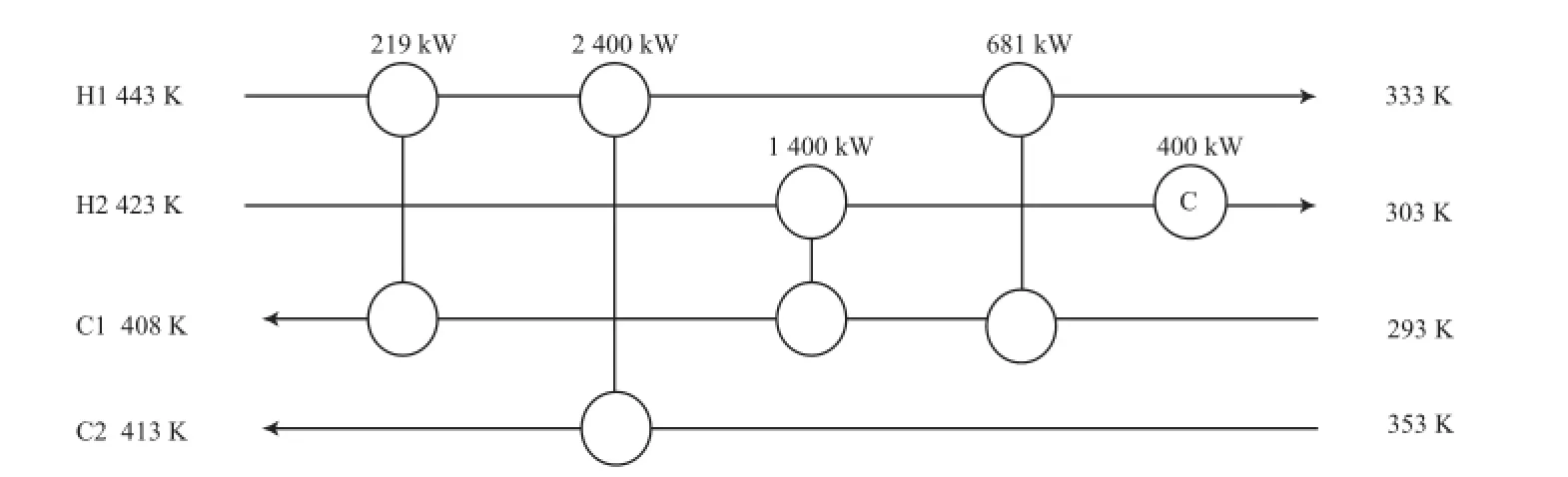
图2 算例1的优化结构Fig.2 Optimal results for case 1.

表2 算例1的优化结果对比Table 2 Comparison of the optimal results for case 1

3.2 算例2

算例2取自文献［19］，是由2股冷流体与2股热流体组成的换热网络问题，相关参数见表3。采用基于局部搜索策略的混沌蚁群算法优化算例2，优化结构见图3，计算所得费用值为11 540 $/a。算例2混沌蚁群算法的计算值与文献方法计算结果的比较见表4。

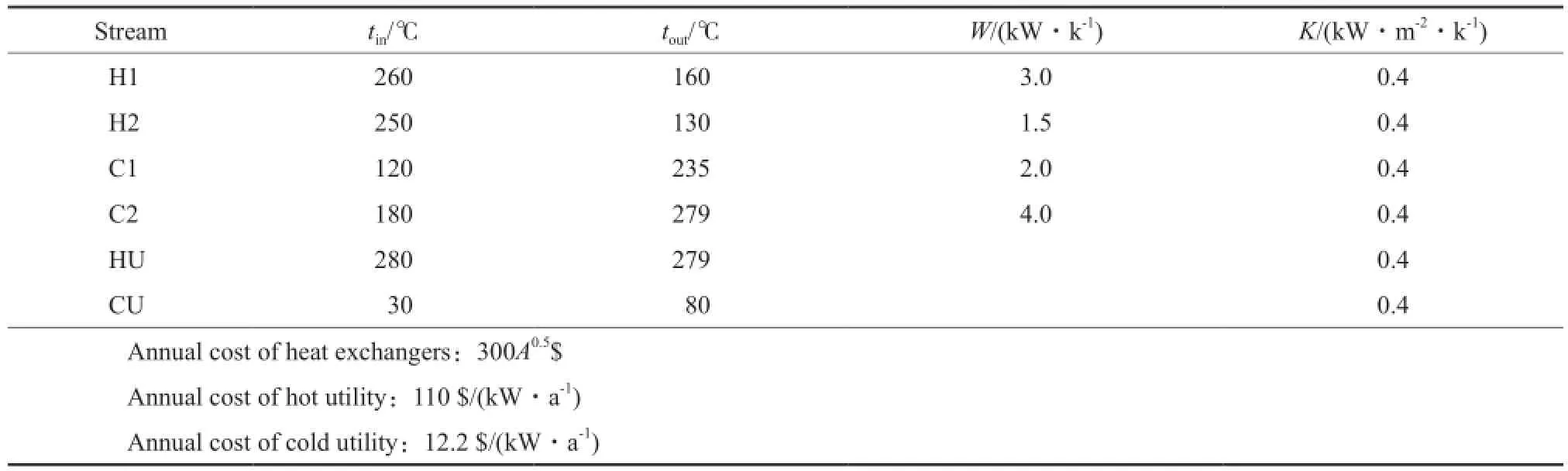
表3 算例2的参数Table 3 Parameters of case 2

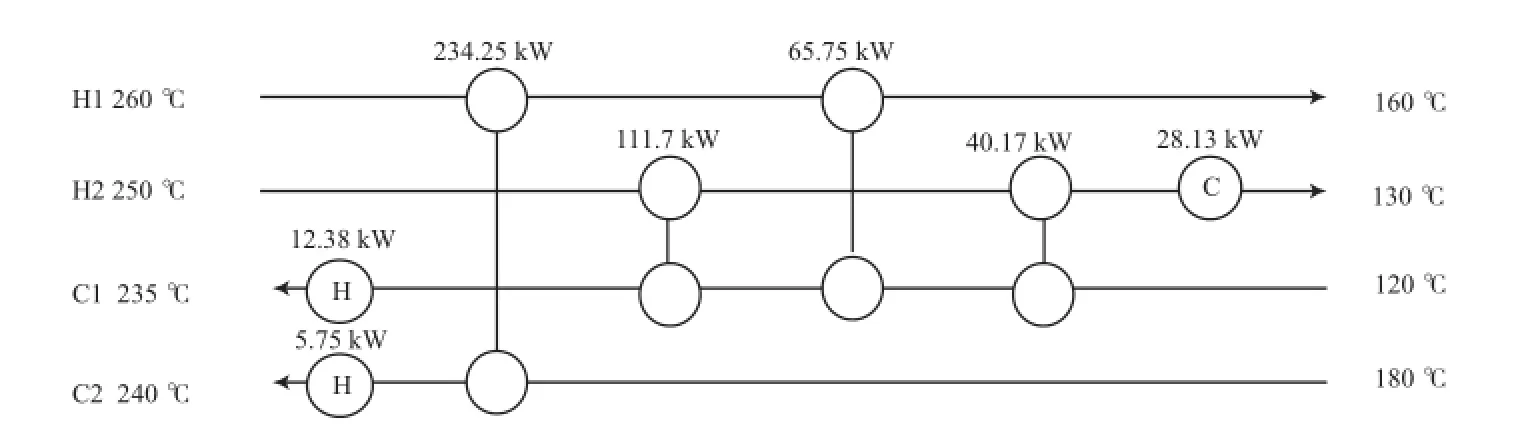
图3 算例2的优化结构Fig.3 Optimal results for case 2.

表4 算例2的优化结果对比Table 4 Comparison of the optimal results for case 2

Ahmad［19］基于一个特定的效率参数XP提出了一种设计换热器最小管壳数的方法，获得的结构对应费用值为12 870 $/a。Nielsen等［20］首先提出了一种新的换热网络结构的表示方法，随后选取模拟退火算法作为优化方法，其所获得结构对应的费用值为12 306 $/a。Khorasany等［21］采用了双层结构算法，即外层使用禁忌搜索算法产生结构，内层采用禁忌搜索算法与序列二次规划法相结合优化换热器的热负荷以及分流比，其获得的结构的费用值为11 895 $/a。Huo等［22］也采用了双层优化算法，外层采用遗传算法产生候选结构，内层采用粒子群法优化热负荷以及分流比，获得的结构对应的费用值为11 632 $/a。

3.3 算例3

算例3取自文献［23］，包含3股热流体、2股冷流体，相关参数见表5。采用基于局部搜索策略的混沌蚁群算法优化算例3，优化结构见图4，计算所得费用值为100 459 $/a。算例3混沌蚁群算法的计算值与文献方法计算结果的比较见表6。

Björk等［23］选用此算例论证有分流分级超结构中流体非等温混合对优化结果的影响，包含了两个换热网络设计。一为基于等温混合模型的设计，对应的费用值为100 720 $/a。另一为基于非等温混合模型的设计，对应的费用值为96 001 $/a。Huang等［24］在有分流分级超结构模型中允许流体进行非等温混合，同时为获得更好的解，改进了温度边界条件并提出了一系列逻辑约束，获得的结构对应的费用值为95 463 $/a。通过对比发现，此结构与Björk等［23］的基于非等温混合模型获得的结构相同，只在连续变量上存在微小的差异。

表5 算例3的参数Table 5 Parameters of case 3

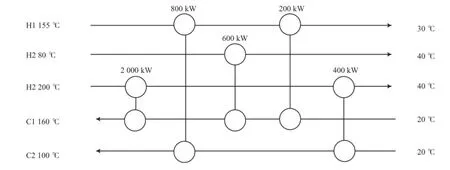
图4 算例3的优化结构Fig.4 Optimal results for case 3.

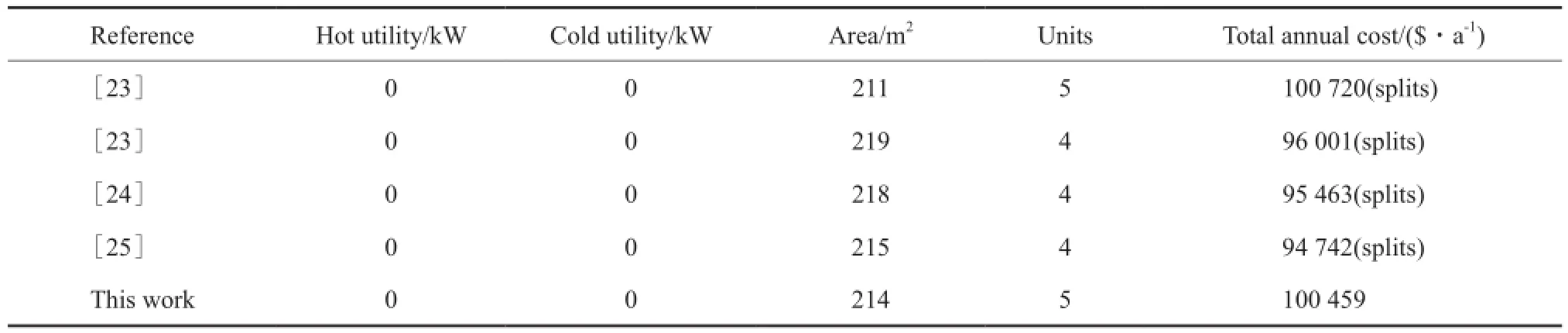
表6 算例3的优化结果对比Table 6 Comparison of the optimal results for case 3

Huang等［25］提出了一种新的基于非等温混合有分流分级超结构模型，即在一条分流上允许存在多个换热器，其所得结构对应的费用值为94 742 $/a。对比混沌蚁群算法的计算值与文献值发现，此算例中的冷量与热量可完全抵消而不需配置公用工程，文献结果间的差异主要归因于模型不同，进而导致温差、换热面积不同。本工作所获得的最优结构同样实现了流体的冷热量完全抵消，可认为此结果是在Grossman无分流分级超结构模型下的最优结构。

由以上3个算例的优化结果可知，混沌蚁群算法能够得到较文献更好的解，表明混沌蚁群算法适用于换热网络综合问题。

4 结论

1） 首次将混沌蚁群算法应用于小规模的换热网络问题，引入Powell法作为局部搜索策略，强化了算法的优化能力。

2） 整型变量判断准则有效地优化了算例中的网络结构，与混沌蚁群算法能够很好地契合，适用于换热网络同步综合。

3） 与文献中采用随机性方法或通过改变模型所获得的结果相比，本工作获得的结果相对更优，可认为是基于Grossmann无分流分级超结构的次优解或最优解，充分证明了混沌蚁群算法优良的局部跳出能力以及全局搜索能力。

符 号 说 明

［1］ Quesada I，Grossmann I E. An LP/NLP based branch and bound algorithm for convex MINLP optimization problems［J］. Comp Chem Eng，1992，16（10）：937 - 947.

［2］ Viswanathan J，Grossmann I E. A combined penalty function and outer-approximation method for MINLP optimization［J］. Comp Chem Eng，1990，14（7）：769 - 782.

［3］ Ravagnani M，Silva A P，Arroyo P A，et al. Heat exchanger network synthesis and optimisation using genetic algorithm［J］. Appl Therm Eng，2005，25（7）：1003 - 1017.

［4］ Yerramsetty K M，Murty C V S. Synthesis of cost-optimal heat exchanger networks using differential evolution［J］. Comp Chem Eng，2008，32（8）：1861 - 1876.

［5］ Silva A P，Ravagnani M A S S，Biscaia Jr E C，et al. Optimal heat exchanger network synthesis using particle swarm optimization［J］. Opt Eng，2010，11（3）：459 - 470.

［6］ Aihara K，Takabe T，Toyoda M. Chaotic neural networks［J］. Phys Lett A，1990，144（6）：333 - 340.

［7］ Chen Luonan，Aihara K. Chaotic simulated annealing by a neural network model with transient chaos［J］. Neural Net，1995，8（6）：915 - 930.

［8］ Zuo X Q，Fan Y S. A chaos search immune algorithm with its application to neuro-fuzzy controller design［J］. Chaos Soli Fract，2006，30（1）：94 - 109.

［9］ Li Lixiang，Yang Yixian，Peng Haipeng，et al. An optimization method inspired by “chaotic” ant behavior［J］. Int J Bifur Chaos，2006，16（8）：2351 - 2364.

［10］ Li Lixiang，Yang Yixian，Peng Haipeng，et al. Parameters identification of chaotic systems via chaotic ant swarm［J］. Chaos Soliton Fract，2006，28（5）：1204 - 1211.

［11］ Cai Jiejin，Ma Xiaoqian，Li Lixiang，et al. Chaotic ant swarm optimization to economic dispatch［J］. Electric Power Sys Res，2007，77（10）：1373 - 1380.

［12］ Li Lixiang，Yang Yixian，Peng Haipeng. Computation of multiple global optima through chaotic ant swarm［J］. Chaos Soliton Fract，2009，40（3）：1399 - 1407.

［13］ Yee T F，Grossmann I E. Simultaneous optimization models for heat integration：Ⅱ. Heat exchanger network synthesis［J］. Comp Chem Eng，1990，14（10）：1165 - 1184.

［14］ Zhang Chunwei，Cui Guomin，Peng Fuyu. A novel hybrid chaotic ant swarm algorithm for heat exchanger networks synthesis［J］. Appl Therm Eng，2016，104：707 - 719.

［15］ Solé R V，Miramontes O，Goodwin B C. Oscillations and chaos in ant societies［J］. J Theory Biol，1993，161（3）：343 - 357.

［16］ Powell M J D. An efcient method for fnding the minimum of a function of several variables without calculating derivatives［J］. Comp J，1964，7（2）：155 - 162.

［17］ 严丽娣，霍兆义，尹洪超. 粒子群算法最优同步综合换热网络［J］. 化工进展，2009（S1）：439 - 442.

［18］ 何巧乐. 双层优化算法处理大规模换热网络［D］. 上海：上海理工大学，2014.

［19］ Ahmad S. Heat exchanger networks：Cost tradeofs in energy and capital［D］. Manchester：University of Manchester Institute of Science and Technology，1985.

［20］ Nielsen J S，Hansen M W，bay Joergensen S. Heat exchanger network modelling framework for optimal design and retroftting［J］. Comp Chem Eng，1996，20（S）：249 - 254.

［21］ Khorasany R M，Fesanghary M. A novel approach for synthesis of cost-optimal heat exchanger networks ［J］. Comp Chem Eng，2009，33（8）：1363 - 1370.

［22］ Huo Zhaoyi，Zhao Liang，Yin Hongchao，et al. A hybrid optimization strategy for simultaneous synthesis of heat exchanger network［J］. Korean J Chem Eng，2012，29（10）：1298 -1309.

［23］ Björk K M，Westerlund T. Global optimization of heat exchanger network synthesis problems with and without the isothermal mixing assumption［J］. Comp Chem Eng，2002，26（11）：1581 - 1593.

［24］ Huang K F，Al-mutairi E M，Karimi I A. Heat exchanger network synthesis using a stagewise superstructure with non-isothermal mixing［J］. Chem Eng Sci，2012，73：30 - 43.

［25］ Huang K F，Karimi I A. Simultaneous synthesis approaches for cost-effective heat exchanger networks［J］. Chem Eng Sci，2013，98：231 - 245.

（编辑 王 馨）

中国科大发现新型广谱光催化制氢技术

中国科学技术大学提出了一种新型的光催化制氢机制，将配位化学的理念引入有机纳米材料中，产品在广谱光照下展现出大幅度提高的光催化制氢性能。

该研究借鉴了均相配位化合物中金属中心与配体分子之间的电荷转移跃迁过程。该金属-配体电荷转移跃迁可以在低于带间跃迁的能量范围内吸光，从而与带间跃迁形成了互补型的广谱吸光。研究人员将有机半导体二维纳米材料作为大分子配体，利用其中的氮原子位点，引入不到千分之一含量的铂离子或者更为廉价的铜离子，形成了金属-有机半导体的纳米配位结构。该极少量的纳米配位单元诱导产生的电荷转移跃迁过程，使得催化剂产品可以在广谱太阳光范围内进行光催化制氢。

DSM公司以尼龙4T牌号扩展生物基聚合物组合Plast Technol，2016 - 06

DSM工程塑料公司公司透露，随着推出高达60%可再生资源衍生的高性能尼龙4T材料的新系列，该公司扩大了其高温耐生物基聚合物范围，以更薄和更可持续的电子设备为目标，新牌号拥有改进的加工窗口。这种新材料称为ForTii Eco，目标针对电子工业中更快、更薄和更可持续的设备的不断增长的趋势。用于电子市场的整个DSM塑料组合不含卤素和红磷，该材料之前在电缆、连接器、智能设备中的框架和天线使用。两种现有的材料是Arnitel Eco TPE以及EcoPaXX尼龙410，两者部分或完全地由可再生资源衍生的，据称新ForTii Eco牌号代表了下一代高温尼龙，能够满足几个方面更加严格的要求。它们提供更高的流动和改进的加工窗口，结合高韧性和充分的耐高温焊接。竞争的半芳香族尼龙如尼龙6T和尼龙10T，不同程度地具有较低的流动性和低韧性。

此外，据ForTii业务经理Konraad Dullaert称，这些材料显示对潮湿的低灵敏度，保证即使在空调状态下也可保持其卓越的机械性能和介电性能。随着数据传输速度不断提高，人们越来越需要像ForTii这样有稳定的介电常数和限制信号损耗的损耗因数的绝缘材料。

日本产综研开发出纳米碳材料新型合成方法

日经技术在线（日），2016 - 05 - 11

日本产业技术综合研究所（产综研）开发出棒状及带状纳米碳材料的新型合成方法。该方法除了采用以往的化学反应和热处理外，不需要其他复杂的工艺，就能简便且高效地合成碳纳米材料。

以往合成石墨烯纳米带采用的是电化学处理和等离子蚀刻等方法，但将碳纳米管剥离、展开存在工序复杂且效率低等问题。而新开发的以配位聚合物为原料的简易合成法，配位聚合物是大量金属离子与有机配位体相互连接，其结构类似于藤架的固体材料。目前，为了将这种材料内部有规则排列的纳米微孔作为有效空间加以利用，全球各地的研究人员都在开展相关研究。其中日本产综研开发的方法是在使用金属盐（乙酸锌）和能够与金属盐结合的有机配体2，5-二羟基对苯二甲酸（交联配体）合成配位聚合物时，加入不能连接金属盐的配体水杨酸（非交联配体）抑制配位聚合物在特定方向的生长，从而合成出棒状的配位聚合物。将这种棒状的配位聚合物放置到惰性气体中，在1 000 ℃下进行加热处理，制备出形状稳定的碳纳米棒。然后在KOH水溶液中对碳纳米棒进行超声波处理后，再在惰性气体中800 ℃下进行热处理激活，叠加成碳纳米棒石墨烯就会分散开，就得到石墨烯纳米带。

这样制备的碳纳米棒和石墨烯纳米带与通常用作电容器电极材料的微孔碳相比具有更高的充放电特性，今后有望成为高效能源储备及转化元件。

中科院固体所在高分散超细铂/还原石墨烯复合材料研究方面取得进展

直接甲醇燃料电池（DMFC）可以将甲醇和氧化剂的化学能直接转化成电能。直接甲醇燃料电池使用的电极催化剂大多为铂基催化剂，而这种催化剂制备成本高，催化活性及稳定性差，阻碍了DMFC的商业化。

中国科学院固体所研发了一种简便且“绿色”的合成方法来制备Pt/rGO纳米复合材料。LAL诱导的高活性锰胶体（MnOx）颗粒能均匀地负载在氧化石墨烯（GO）纳米片上，形成MnOx/rGO纳米复合材料。这种高活性的MnOx颗粒不但能作为还原剂，而且还能作为牺牲模板原位固定被还原的超细Pt纳米颗粒。最终得到的Pt纳米颗粒粒径大约在1.8 nm左右，且均匀地分布在rGO纳米片上。与商用的Pt/C催化剂相比，无论是在酸性还是碱性介质中，这种Pt/rGO催化剂对甲醇氧化均展现出较高的催化活性和稳定性。上述研究结果表明，合成的Pt/rGO催化剂在DMFC方面具有潜在的应用前景，且该合成方法为今后贵金属/石墨烯纳米复合材料的合成提供了一种新的思路。

Design of small-scale heat exchanger networks by chaotic ant swarm algorithm

Zhang Chunwei，Cui Guomin
（Research Institute of New Energy Science and Technology，University of Shanghai for Science and Technology，Shanghai 200093，China）

Because of serious non-convex and non-linear problems in heat exchanger networks synthesis，a chaotic optimization algorithm，namely chaotic ant swarm algorithm(CAS)，was proposed for the synchronous synthesis of the heat exchanger networks. The search ability and features of CAS were verifed with complicated small-scale heat exchanger network synthesis as the investigated subject. The Powell method was introduced as local search strategy to enhance the accuracy and stability of CAS. Three diferent cases based on small-scale heat exchanger networks were calculated by means of the proposed algorithm and the obtained solutions were compared with results published in literatures，which showed the excellent search ability of CAS.

heat exchanger network synthesis；chaotic ant swarm algorithm；Powell method

1000 - 8144（2016）10 - 1248 - 08

TQ 021.8

A

10.3969/j.issn.1000-8144.2016.10.016

2016 - 04 - 05；［修改稿日期］ 2016 - 07 - 06。

张春伟（1992—），男，内蒙古自治区通辽市人，硕士生，电话 13524420426，电邮 zcwaxc@163.com。联系人：崔国民，电话 021 - 55271466，电邮 cgm1226@163.com。

国家自然科学基金项目（51176125）。