用曲波变换消除VSP数据处理中的空间假频与采样不规则

彭军，韩立国，周家雄，王宇,隋波，李海鹏

(1.中海石油(中国)有限公司湛江分公司,广东湛江 524057；2.吉林大学地球探测科学与技术学院,吉林长春 130026)

用曲波变换消除VSP数据处理中的空间假频与采样不规则

彭 军1,2，韩立国2，周家雄1，王 宇1,隋 波1，李海鹏1

(1.中海石油(中国)有限公司湛江分公司,广东湛江 524057；2.吉林大学地球探测科学与技术学院,吉林长春 130026)

由于条件与经费的限制，在实际地震资料采集过程中，常常会遇到获得的地震资料较稀疏或不规则，导致空间假频、采样不规则的问题，影响地震资料的成像效果。可利用地震道空间插值来解决这些问题，提升地震数据处理结果品质。曲波变换的基函数是具有倾角、频率、时间三方面同时局部化的函数，它可以对空间信号做稀疏表达，适合地震资料的插值处理。本文采用该方法对理论模型数据和实际VSP数据作插值处理，解决不规则采样、空间假频问题。实际应用表明该方法精度高，插值准确，处理结果的振幅和同相轴连续性好。

曲波变换 空间假频 VSP 插值

Peng Jun，Han Li-guo，Zhou Jia-xiong，Wang Yu，Sui Bo，Li Hai-peng. Removing spatial alias frequency and irregularity of sampling in VSP data processing by using curvelet transform[J].Geology and Exploration，2016,52(3):0537-0542.

1 引言

随着油气勘探开发不断深入，油气勘探、开发由构造油藏转向岩性油藏，由厚层油气藏向薄层油气藏迈进。在复杂的地质条件下，提高钻探成功率，钻前地质研究与认识对边际油气藏的勘探、开发显得尤为重要。地震资料作为认识地下地质情况的重要手段，地震资料的好坏，将极大的限制地质人员对地下情况认知的质量。良好的地震资料品质将极大提高地质人员对地下地质情况认识的精度。无论海洋地震勘探、陆地地震勘探，还是VSP(垂直地震剖面)采集，由于资金和采集技术发展水平的限制，野外地震采集往往存在假频和不规则采样的问题，特别是海洋三维地震的联络线方向。海上油气勘探、开发相对陆地油气勘探、开发成本更高，对钻前地下地质条件认识要求更高，这就需要拥有质量品质优良的地震资料为地质研究人员提供较精细的地质认知条件。VSP数据为时间与深度记录格式，相比于传统地震资料具有分辨率高、具有深度信息等优势，使VSP数据处理近年来受到极大关注。

地震资料反射波勘探是对中深层地层识别的有效方法,广泛应用于油气与金属矿床成像(徐明才等，1999；梁光河等，2001；孙明等，2001；徐明才等，2005；李战业等，2009)，然而地震资料处理过程中的很多算法(如直达波分离处理、去多次波处理(SRME)、偏移成像处理等)都需要规则且密集的地震采样，就需采用恰当的方法将不规则采样处理为规则采样。在VSP采集中由于成本控制，一般在目的层段采集样点较为密集，在非目的层段采集样点较为稀疏。由于采样的不规则和空间采样较稀疏将产生空间假频。空间假频的存在会导致频散现象，无法得到较好的地震资料成像，使解释人员无法正确认识地下地质情况。目前，地震道插值和面元均化等处理技术，都在努力解决空间假频和不规则采样的问题，采用这些方法处理后的数据含有的地球物理信息更加真实地反映地下地质体，更有利于进行构造解释和地震地层学的研究。所以地震资料去假频和规则化是地球物理研究中的一个难点与热点问题，近20多来一直受到专业人员的关注和重视。

常见的地震资料插值技术主要有：T-X预测误差滤波插值方法，抗假频F-X域地震道插值方法、f-k域插值(李学聪等，2009)、Radon域插值等。这些传统的插值方法都存在它们各自的问题：有的是计算量太大，在实际地震资料处理中可用性大大降低；有的是插值系数不能为任意数；还有的是不能正确内插空间假频地震道。我们希望插值技术不仅可以解决不规则采样问题，同时也解决空间假频问题。针对以前算法的不足，最近也发展了很多新的算法(高建军等，2011，刘喜武等，2011)，希望寻找到一种既准确又易于快速实现的计算方法。

在1999年，Candesetal.(1999)提出了曲波变换(curvelet transform)，构建了曲波变换的数学理论基础。2006年，Candes发布了曲波变换的快速算法(第二代曲波变换数值算法)(Emmanueletal.，2005)，计算效率大大提高。2007年，Demanet和Ying发表了镜像延伸的曲波变换算法。最近一些年，曲波变换不仅理论上得到了快速的发展，并在工业计算中发挥了重要作用，广泛的应用在数字信号处理方面。曲波变换具有时频局部化、倾角局部化的性质；地震资料是分段连续、具有不同倾角的地震同相轴组成，地震资料也具有时倾角局部特性，因此将曲波变换能够稀疏的表达地震资料，更加适合地震资料去噪、插值、多次波去除等方面的处理研究(Neelamani，Retal.，2008；彭才等，2008；Kumar Vetal.，2009；仝中飞等，2009；Mostafa Naghizadehetal.,2010；薛念，2010；周家雄等，2010；刘磊等，2011； Jing Wangetal.，2013)。

2 基本原理

第一代曲波变换需要进行子带分解、平滑分块、正则化和Ridgelet分解实现曲波变换，这就导致了巨大的数据冗余，计算效率低下。第二代曲波变换脱离了Ridgelet理论，计算速度和计算冗余都得到了改善。第二代曲波变换的计算复杂程度满足O(n2logn)，它的逆变换不仅准确，并且逆变换的计算复杂程度也满足O(n2logn)。快速离散曲波变换算法的实现有三种算法：一种是基于不规则采样的快速傅立叶变换设计的算法，第二种是基于外推算法的快速曲波变换，还有一种是最新的基于镜像外推的快速算法(周家雄等，2010)。

(1)

对于每一个j≥j0，可以用傅立叶变换定义频率窗Uj，即

(2)

其中⎣j/2⎤是j/2的整数部分。所以，Uj是一个带方向的楔状体，它等于半径窗函数和角度窗函数的乘积，且具有对称性，Uj(r,θ)+Uj(r,θ+π)，如图1所示。

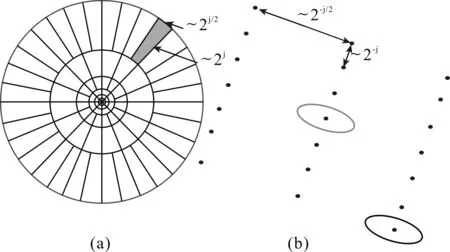
图1 频域和时域曲波Fig.1 Curvelets in frequency domain and time domain a-频域；b-时域a-frequency domain;b-time domain

(3)

其他2-j尺度的曲波函数都可以由该母函数φj(x)经过旋转、平移得到。

(4)

其中Rθ是旋转函数，θ是旋转角，

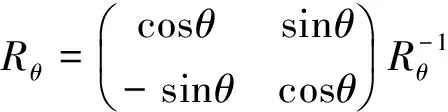
(5)

把上式带入到频率域中，可以得到

(6)

从曲波变换的原理可知曲波变换具有多分辨率分析以及时频局部性的特点，更重要的具有局部方向特性。在进行地震插值时，将缺失道标记为0，非缺失道标记为1，这样在计算时只针对缺失道进行数据填充，已有数据不被改变。然后对地震数据进行曲波变换，得到曲波系数。因为地震数据在曲波域是稀疏的，在曲波局部方向特性的控制下，缺失的地震数据可以通过相近地震道曲波变换系数得到相应的曲波系数。将得到的曲波系数经过曲波逆变换，就可以将缺失的地震数据填补上，达到插值的目的。

地震资料空间假频是由于地震资料采样不规则或采样太稀疏导致的，因此当地震数据空间采样规则、密度足够时，就能有效去除空间假频。

3 模型实验

地震资料的空间假频与地震同相轴的倾角关系密切。为了避免空间假频的出现，大倾角同相轴需要更小的空间采样间隔。本文采用40赫兹的雷克子波所组成的不同倾角的同相轴，共150道，如图 2a所示。模型数据的同相轴都是向右方向倾斜的，那么它的f-k谱的波数应该是正值。但是由于空间采样不足，大倾角的同相轴出现了假频的现象，模型数据的f-k谱的部分能量被划入了负象限。

为了消除空间假频现象，采用曲波进行均匀采样数据内插。通过1 ∶1的等间距插值处理，成功的解决了假频问题，处理后的数据的f-k谱的能量都恢复到了正象限，如图2b所示。

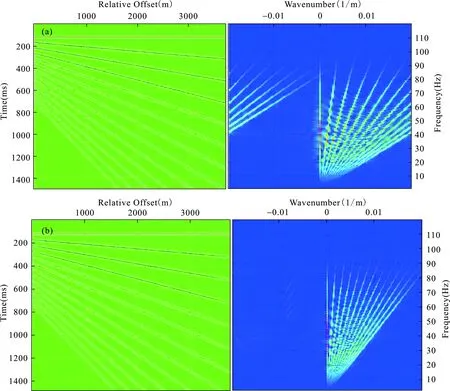
图2 去假频处理实验Fig.2 Experiment of removing alias a-存在假频的地震数据及其频谱；b-插值后的地震数据及其频谱a-eismic data and its spectrum with alias;b-interpolated seismic data and its spectrum

设计如图3a所示模型，研究在地震道缺失的情况下，该算法同时处理空间假频和不规则采样的能力。该数据不仅缺失道，同时也存在假频的影响，见图 3a。图 3b是插值处理后结果及其f-k谱。该结果表明，本文方法不仅可以消除假频，而且可以把缺失的数据补齐，达到均匀采样的目的。

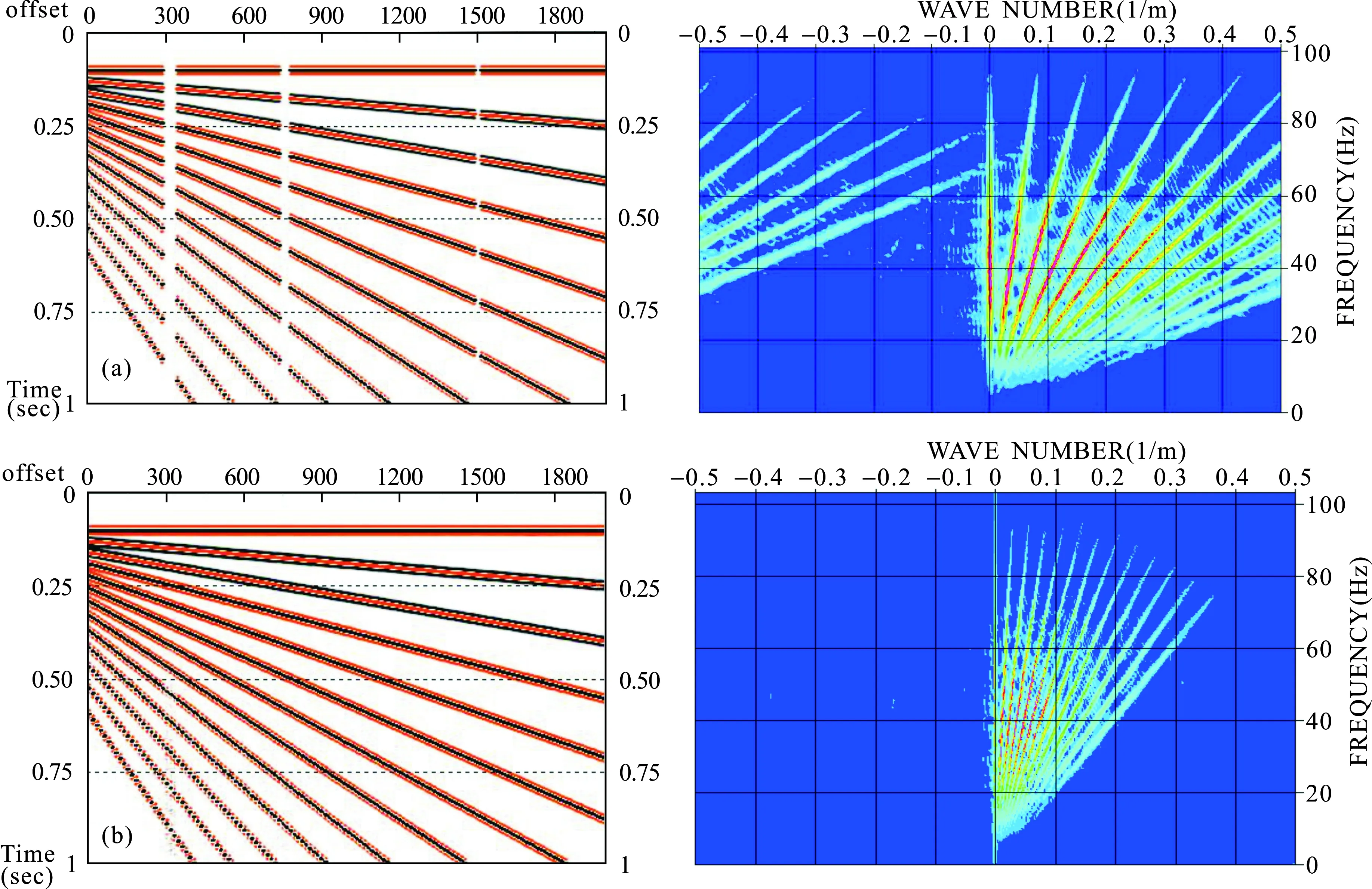
图3 缺失数据的模型及其数据恢复处理结果Fig.3 Missing data model and data recovery processing results a-不规则地震数据及其频谱；b-插值后的地震数据及其频谱a-irregular seismic data and its spectrum;b-interpolated seismic data and its spectrum

4 VSP数据处理

为了节省成本与时间，在非目的层层段，VSP野外采集的空间采样间隔都比较大。本次VSP采集用的是Sercel GeoWaves2级3分量检波器，2级检波点距离10m，在非目的层段炮检距40m，在目的层段炮检距20m。所以，非目的层的数据缺值达到了50%，同时这批数据也是不规则采样。本次插值运算的目的是补齐非目的层段缺失的数据。如图 4a所示，由于不规则采样，地震数据的f-k谱出现了类似假频的干扰。通过曲波变换插值处理，空间假频消除了，f-k谱更加符合理论，同相轴和振幅连续性好,如图4b所示。

5 结论

地震资料作为认知地下地质情况的基础资料，其品质的好坏直接决定了地质人员对地下地质情况认知的精度。地震资料的规则化与去假频是地震资料处理中的一个重要步骤。本文采用曲波变换进行VSP资料的规则化与去假频处理，通过理论模型实验表明，曲波变换能进行等间隔与非等间隔插值，采用该方法能有效去除假频，保证插值后的地震数据相位的精度。插值后VSP数据同相轴、振幅连续，频谱图清晰的显示插值前后仅有假频被去除，有效频率未有变化。将曲波变换插值应用于实际VSP数据表明，使用曲波变换的插值结果能有效去除空间假频，VSP数据信噪比高，振幅的局部特性保持较好。采用曲波变换对模型与实际VSP数据插值结果表明该方法计算结果准确，具有良好的实用性。曲波变换的高精度、振幅属性的局部保持特性对于高保真地震资料的处理将带来极大的帮助，有利于后续储层预测的顺利进行。

图4 插值处理前后VSP地震数据对比及频谱的变化Fig.4 Comparison of VSP seismic and spectra before and after interpolation and their variations a-处理前VSP地震数据与频谱；b-处理后VSP地震数据与频谱a-before processing;b-after processing

本文仅将该方法应用于VSP数据处理，下一步我们研究把该方法应用在海洋拖缆数据中。研究当海缆采集地震资料连续缺失大块数据时，如何使用曲波进行插值处理，重构该区地震资料。

Candes E J，Donoho D L. 1999. Curvelets: a surprisingly effective nonadaptive representation of objects with edges[C]. Curves and Surfaces，Vanderbilt University Press，Nashville，TN.: 1-16

EmmanuelCandès，Laurent Demanet，David Donoho，Lexing Ying. 2005.Fast Discrete Curvelet Transforms[J]. Siam Journal on Multiscale Modeling & Simulation，5:861-899

Gao Jian-jun，Chen Xiao-hong，Li Jing-ye. 2011. The reconstruction method for 3D irregular seismic data[J]，Oil geophysical prospecting,46(1):40-47 (in Chinese with English abstract)

Jing Wang，Xuekai Sun，Sam Zandong Sun. 2013. Seismic denoising in curvelet domain: an adaptive thresholding based on local variance analysis[C]. SEG Houston 2013 Annual Meeting: 4309-4313

Kumar V.，Herrmann，F. 2009. Incoherent noise suppression with curvelet-domain sparsity[C]. Technical Program Expanded Abstracts:3356-3360

Li Xue-cong，Liu Yi-ke，Chang Xu，Jin De-gang，Zhang Heng-chao.2009. Interpolation for seismic traces based on F-K migration and demigration [J]. Progress in Geophysics,24(6):2020-2029 (in Chinese with English abstract)

Li Zhan-ye，Yin Jun-jie，Wang Yun. 2009. The application of the numerical simulation and imaging of seismic scattered wave in exploration of metal mineral deposits [J]. Geology and Exploration,45(2):80-84 (in Chinese with English abstract)

Liang Guang-he，Cai Xin-ping，Zhang Bao-lin,Xu Xing-wang. 2001. The application of seismic exploration method in deep prediction of gold deposits [J]. Geology and Exploration，37(6):29-33 (in Chinese with English abstract)

Liu Lei，Liu Zhen，Zhang Jun-hua. 2011. Denoising and detecting seismic weak signal based on curvelete thresholding method. Progress in geophys,26(4):1415-1422 (in Chinese with English abstract)

Liu Xi-wu，Liu Hong，Liu Bin. 2004. Astudy on algorithm for reconstruction of De-alias uneven seismic data[J]. Chinese Journal of geophysics，47(2) :299-305(in Chinese with English abstract)

Mostafa Naghizadeh，Mauricio D. Sacchi. 2010. Beyond alias hierarchical scale curvelet interpolation of regularly and irregularly sampled seismic data. Geophysics，75(6):189-202

Neelamani R，A. I. Baumstein，D. G. Gillard，M. T.Hadidi，W. L. Soroka. 2008. Coherent and random noise attenuation using the curvelet transform[J]. The Leading Edge，27(2):240-248

Peng Cai，Chang Zhi，Zhu Shi-jun. 2008. Seismic data denoising by curvelet transformation[J]. Geophysical prospecting for petroleum,47(5):461-464(in Chinese with English abstract)

Sun Ming，Lin Jun. 2001. Study of seismic scattering wave field numerical model for metallic ore exploration [J] . Geology and Exploration，37(4):68-70 (in Chinese with English abstract)

Tong Zong-fei，Wang De-li，Liu Qi. 2009. The study on seismic data Interpolation with Curvelet thresholding iterative method[C].Chinese Geophysics:66(in Chinese with English abstract)

Xu Ming-cai，Gao Jing-hua，Chai Ming-tao，Wang Guang-ke，Liu Jian-xun，Rong Li-xin. 1999. Seismic technique applied to active fault assessment [J]. Geology and Exploration，35(1):36-40 (in Chinese with English abstract)

Xu Ming-cai，Gao Jing-hua，Rong Li-xin，Chai Ming-tao，Lv Qing-tian，Shi Da-nian. 2005. Combining exploration technique of the ground seismic tomography and the high-resolution seismic method[J]. Geology and Exploration,41(4): 83-87 (in Chinese with English abstract)

Xue Nian.2010. Curvelet transformation for seismic data denoising and interpolating[D]. Xi’an Jiao Tong University master thesis:5-6(in Chinese with English abstract)

Zhou Jia-xiog，Wang Yu，Guo Ai-hua，Sun Yue-cheng，Li Hai-peng.2010. A study on denoising poststack 3D seismic data by Curvelet transform [J]. China Offshore Oil And Gas，22(1):17-21(in Chinese with English abstract)

[附中文参考文献]

高建军,陈小宏,李景业.2011.三维不规则地震数据重建方法[J]. 石油地球物理勘探,46(1):40-47

李学聪,刘伊克,常 旭,金德刚,张恒超.2009.基于F-K偏移和反偏移的地震道插值方法研究[J]. 地球物理学进展,24(6):2020-2029

李战业,尹军杰,王 赟.2009.地震散射波模拟成像在金属矿勘探中的应用[J]. 地质与勘探,45(2):80-84

梁光河,蔡新平,张宝林,徐兴旺.2001.浅层地震勘探方法在金矿深部预测中的应用[J]. 地质与勘探,37(6):29-33

刘 磊,刘 振,张军华.2011. 曲波阈值法地震弱信号识别及去噪方法研究[J].地球物理学进展,26(4):1415-1422

刘喜武,刘 洪,刘 彬.2004.反假频非均匀地震数据重建方法研究[J]. 地球物理学报,47(2):299-305

彭 才,常 智,朱仕军.2008.基于曲波变换的地震数据去噪方法[J]. 石油物探,47(5):461-464

孙 明,林 君.2001.金属矿地震散射波场的数值模拟研究[J]. 地质与勘探,37(4):68-70

仝中飞,王德利,刘 琦.2009.Curvelet阈值迭代法在地震数据插值中的方法研究[C]. 中国地球物理:66

徐明才,高景华,柴明涛,王广科,刘建勋,荣立新.1999.应用于评价活动断层的地震方法技术[J]. 地质与勘探,35(1):36-40

徐明才,高景华,荣立新,柴铭涛,吕庆田,史大年.2005.地面地震层析成像和高分辨率地震联合勘探技术[J]. 地质与勘探,41(4):83-87

薛 念. 2010. 基于Curvelet变换的地震数据插值和去噪[D]. 西安交通大学硕士论文:5-6

周家雄,王 宇,郭爱华,孙月成,李海鹏. 2010. 基于三维曲波变换的叠后三维地震资料去噪处理研究[J]. 中国海上油气,22(1):17-21

Removing Spatial Alias Frequency and Irregularity of Sampling in VSP Data Processing by Using Curvelet Transform

PENG Jun1,2，HAN Li-guo2，ZHOU Jia-xiong1，WANG Yu1，SUI Bo1，LI Hai-peng1

(1.ChinaNationalOffshoreOilCompany，ZhanjiangBranch，Zhanjiang，Guangdong5240571; 2.CollegeofGeoExplorationScienceandTechnology，JilinUniversity，Changchun,Jilin130026)

Spatial alias frequency and irregularity of sampling are often encountered in seismic acquisition due to limited conditions and funds，which can affect many aspects of seismic processing. Seismic interpolation can be used to solve these issues to improve the quality of seismic data processing. To do so，the curvelet transform decomposes the seismic data into local wavelets which have local time-frequency and local dip attributes. Spatial signal can be expressed sparsely by curvelet transform，so is suitable for seismic data interpolation. In this paper，we employ the curvelet transform to solve the problems of spatial alias frequency and irregular spatial sampling. The tests on model data and real VSP field data show that this method can achieve high precision，accurate interpolation and good continuity in amplitude and co-phase axes.

curvelet transform，spatial aliasing，VSP，interpolation

2015-09-15；

2016-04-15；[责任编辑]陈伟军。

中海石油(中国)有限公司南海西部海域典型低孔低渗油气藏勘探开发关键技术研究及实践(编码:CNOOC-KJ125ZDXM07LTD02ZJ11)赞助。

彭 军(1984年-)，在读硕士，工程师，现从事地球物理解释与处理技术的研究和应用工作。E-mail:pengjun@cnooc.com.cn。

P315

A

0495-5331(2016)03-0537-06