基于Copula函数的流域内降雨丰枯遭遇研究

吕振豫,穆建新

(1.流域水循环模拟与调控国家重点实验室,北京 100038;2.中国水利水电科学研究院,北京 100038)

不同水文区的丰枯遭遇问题作为近年来降雨、径流频率分析的研究重点,对合理利用流域间丰枯互补、相机补水具有重要意义,可为流域水资源合理分配提供参考。研究不同区域水文事件的丰枯遭遇问题,实质上是求取具有线性或者非线性关系多元变量联合分布的过程。传统建立多变量联合分布的方法或假定变量为独立分布,或认为多变量联合分布存在固定格式,具有较大的局限性。Copula函数作为一种新型的建立多变量联合分布的有效工具,克服了传统方法在变量分布上的局限性,目前在水文事件频率分析中广泛使用。Copula函数理论最早的详细介绍要追溯到Joe[1]和Nelsen[2]的研究。Michele等[3]首次将Copula理论运用到水文频率分析中,利用Frank和Archimedean copula函数簇描述了流域降雨强度与降雨历时的相关性。而后Copula函数大量应用于水文频率分析,主要集中在水文事件丰枯遭遇问题研究以及水文要素二维和多维联合分布的建立方面。闫宝伟等[4]运用二维Copula函数构造了南水北调中线工程水源区与各受水区汛期、非汛期及全年降雨的联合分布。Jenq等[5]以干旱历时和干旱强度为研究对象,利用二维Clayton函数建立了2个干旱要素的联合分布,计算了干旱事件的发生概率及其重现期,打破了传统只利用一个指标分析干旱发生特征的局面;谢华等[6]利用三维Copula函数建立了长江、淮河、黄河3个区域的联合分布模型。冯平等[7]尝试采用四维Copula函数构造径流系列的联合分布,分析南水北调西线工程水源区河流与受水区的丰枯遭遇问题。除此之外,Copula函数在暴雨[8-10]、洪水[11-14]等极值事件的多特征属性频率分析中也得到大量应用。

图1 研究区域及站点分布

笔者以东江流域典型站点实测降雨系列丰枯遭遇问题为研究背景,运用Copula函数构建三维联合分布模型,计算分时段不同量级降雨事件的遭遇概率及条件概率,验证三维Copula函数是否适用于建立具有较强相关性系列的联合分布模型。

1 数据与方法

1.1 数据来源

东江作为珠江水系的三大河流之一,是河源、惠州、东莞、深圳等地的主要供水水源,承担着向香港供水的任务[15]。流域全长562 km,面积达27 040 km2,占珠江流域总面积的5.96%。东江自东北向西南流入广东省境内,经过龙川、河源、紫金、惠阳、博罗、东莞等县注入狮子洋。东江流域属于亚热带季风湿润气候区,具有明显的干湿季节,汛期多年平均降水量1 200～1 500 mm,非汛期多年平均降水量300～500 mm。

本文选取分布于东江流域上、中、下游的龙川、河源和博罗3个代表性水文站点(图1)1956—2005年月尺度实测降雨资料作为研究对象,分汛期(4—9月)、非汛期(10—次年3月)以及全年3个时段开展对比研究。文中所用数据均经过一致性、代表性、可靠性审查。

1.2 三维Copula函数理论

Copula函数是边缘分布为[0,1]区间均匀分布的联合分布函数。构造Copula函数的理论基础是Sklar定理,即,设X、Y、Z为连续的随机变量,边缘分布函数分别为F(X)、F(Y)和F(Z),F(X,Y,Z)为3个变量的联合分布函数,如果F(X)、F(Y)、F(Z)连续,则存在唯一的函数Cθ(u1,u2,u3)满足:

F(X,Y,Z)=Cθ(F(X),F(Y),F(Z))∀X,Y,Z

(1)

式中:Cθ(u1,u2,u3)为Copula联合分布函数,θ为copula函数的待定参数。

表1 常用三维阿基米德Copula函数

Copula函数的主要构造类型有3种,包括椭圆型、二次型以及阿基米德型。其中具有单参数特征的阿基米德型Copula函数结构简单、计算方便,可构造的形式多样,并且适应性强,目前在丰枯遭遇问题研究中得到广泛应用。阿基米德型Copula函数主要通过算子φ构造而成,n维阿基米德Copula函数定义为

Cn(u1,u2,u3)=φ[-1][φ(u1)+

φ(u2)+…+φ(un)]

(2)

(3)

式中:C(u1,u2,u3)为随机变量X,Y,Z的联合分布函数,表示变量间的相关结构;ui=F(X)为各变量的边缘分布函数,μ1,μ2,μ3分别为随机变量的边缘分布概率;φ为阿基米德生成算子,为连续、严格递减函数,φ(0)=∞,φ(1)=0;φ-1为φ的反函数。

当构造Copula函数的算子φ不相同时,所构造出的Copula函数也存在很大差别。表1为水文事件丰枯遭遇研究中较为常用的三维阿基米德Copula函数。

Copula函数的参数估计方法有很多[16],目前较常用的是非参数法和两阶段估计方法,非参数法要求获得明确的Kendall′τ与Copula参数θ的表达式,仅适用于二维阿基米德型Copula函数的参数估计,同时这种方法易受资料长度的影响,精度不够。两阶段估计方法则精度较高,适用于多维Copula函数的参数估计。本文采用两阶段估计方法确定三维Copula函数的参数。

两阶段参数估计方法是将随机变量的边缘分布参数和Copula联合分布参数分别进行估计,主要通过以下过程实现。

极大似然法估计边缘分布参数:

(4)

极大似然法估计Copula函数中的参数θ:

(5)

构造的Copula联合分布模型是否适合,能否描述变量间的相关性结构,则需要通过拟合优度检验来确定,最终选取拟合优度最高的作为最终模型,进行丰枯遭遇分析。本文通过Kolmogorov-Simirnov检验对Copula函数模型进行拟合检验。采用赤池信息法(Akaike information Criterion,AIC)优选待定参数不同的Copula函数模型,AIC最小为最优。采用离差平方和(OLS)最小准则对Copula函数进行拟合优度评价。具体定义见表2。

表2 拟合优度检验项目计算公式

注:F(xk,yk,zk)为xk,yk,zk的联合分布;mk为联合观测值样本中同时满足x≤xk,y≤yk,z≤zk的观测值个数;n为样本长度;RSS为模型拟合后的残差平方和;Pi,Pei分别为联合分布的理论频率和经验频率。

2 流域内丰枯遭遇联合分布模型建立

2.1 各站点降雨边缘分布确定

目前我国水文分析中一般假定降雨、径流服从P-Ⅲ型分布,其概率密度函数为

(6)

式中:α、β和a0分别为形状、尺度和位置参数。

表3 P-Ⅲ型曲线特征参数

表4 边缘分布拟合优度检验参数计算结果

表5 相关系数计算结果

鉴于流域内上、中、下游地理、气候特征的差异性,P-Ⅲ型分布并非普适。基于Copula函数建立流域降雨变化的联合分布模型不限定变量的分布线型,因此,选取拟合优度最好的边缘分布,成为决定联合分布模型拟合精度大小的关键。本文选取P-Ⅲ型分布、对数正态分布及指数分布作为待选边缘分布,降雨变化经验频率采用下式计算:

(7)

式中:F(X)为表示概率的代表函数;P(X≤xm)为经验频率,m为xm对应序号,N为样本容量。

通过计算各分布线型理论频率对于降雨变化经验频率的RSquare(确定系数)、RMSE(均方根误差)及AIC值(赤池信息准则),并择优选取,计算及选取结果见表4。从表4可以看出,3个站点汛期、非汛期、全年3个时段各线性拟合确定系数RSquare均在0.8以上,最高达0.997,说明3个线性拟合精度都较高。根据RMSE和AIC最小准则,以年尺度为例,可以看出龙川站年尺度降雨变化对数正态分布拟合的RMSE及AIC值较P-Ⅲ分布和指数分布小,因此,选取对数正态分布作为龙川站年尺度降雨变化的边缘分布;对河源、博罗站而言,P-Ⅲ型分布拟合参数RMSE及AIC明显小于其他2个分布线型,因此选取P-Ⅲ型分布作为河源和博罗站年尺度降雨变化的边缘分布。

2.2 初选Copula函数

阿基米德Copula函数对于变量的相关性有一定的要求,其中Clayton Copula函数和Gumbel-Hougaard Copula函数适用于具有正相关关系的随机变量,Frank Copula函数则对正、负相关关系的随机变量都适用。可根据3个站点不同时段降雨变化相关性的大小初步选取Copula函数。为此,首先分析3站点各时段降雨变化的相关性大小,见表5。从表5可知,上、中、下游3个站点降雨变化两两相关系数均在0.6以上,其中龙川-河源站非汛期降雨相关系数最大达0.93,说明3个站点降雨变化具有较强正相关性。综合考虑,最终选取Clayton Copula函数和Gumbel-Hougaard Copula函数作为联合分布模型建立的初选函数。

2.3 Copula函数参数估计及拟合优度检验

Copula函数的参数θ根据公式(4)～(5)进行估计(结果见表6)。为确定最优Copula函数,建立联合分布模型,需要对初选的2个Copula函数进行拟合优度检验,以分析比较3个站点不同时段降雨变化观测点的经验累积频率与理论累计频率的一致性。对3个站点不同时段降雨变化的观测值(xi,yi,zi)按x升序排列,得到新数据组(x1,y1,z1),(x2,y2,z2),…,(xN,yN,zN),三维经验联合概率计算公式为

F(xi,yi,zi)=P(X≤xi,Y≤yi,Z≤zi)=

(8)

式中:P为经验联合频率,m为同时满足xj≤xi,yj≤yi,zj≤zi的观测点个数(i≤j,1≤i≤N,1≤j≤N);N为样本容量。

降雨变化经验联合频率与理论联合频率的一致性检验结果见图2。因篇幅限制,文中只给出年尺度拟合结果。从图2可知,Clayton Copula函数与Gumbel-Hougaard函数构造的理论联合分布模型对经验联合频率的一致性均较强,线性相关系数在0.97以上。计算得到汛期、非汛期降雨变化2种Copula函数构造的理论联合分布频率,与经验联合分布频率一致性也较高。这说明仅通过一致性检验不足以选取最优的Copula函数。

图2 年尺度降雨变化经验联合频率与理论频率一致性检验

为更有效地选取最优Copula函数,通过K-S检验,采用OLS、AIC最小准则等进行拟合优度检验,检验结果见表6。通过对比分析发现,在0.05置信水平下,K-S检验统计量D均小于标准值D50,0.05=0.189(50是自由度、0.05是置信水平),说明初选Copula函数均能通过K-S检验。观察可知,就离差平方和DOLS及AIC的大小来看,Gumbel-Hougaard Copula函数明显小于Clayton Copula函数,表明Gumbel-Hougaard Copula函数拟合精度更高。

图3为3个站点不同时段2个Copula函数建立的理论模型与经验联合频率的拟合情况,进一步验证了Gumbel-Hougaard Copula函数较Clayton Copula函数拟合效果好。最终选取Cumbel-Hougaard Copula函数作为3站不同时段降雨变化联合分布模型的构造函数。

表6 3个站点降水丰枯遭遇Copula函数 拟合优度检验及参数估计结果

图3 不同时段经验联合频率与理论频率拟合结果

3 结果分析

3.1 3个站点不同时段丰枯遭遇分析

得到各时段降雨变化的边际分布,选定最优Copula函数,然后据此建立3个站点分时段降雨变化丰枯遭遇联合分布模型。龙川站、河源站、博罗站不同时段降雨量达到某一概率时的联合概率分布表示为

F(x,y,z)=P(X≤x,Y≤y,Z≤z)=

C(FX(x),FY(y),FZ(z))=C(u1,u2,u3)=

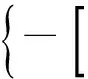
(9)

式中:θ为Gumbel-Hougaard Copula函数的参数,因计算时段的不同而异;X,Y,Z分别为龙川、河源、博罗站降雨系列值;u1=FX(x),u2=FY(y),u3=FZ(z)分别为龙川、河源、博罗站降雨边缘分布函数。

根据降雨量的大小将来水情况分为丰、平、枯3个等级,取丰、枯划分相应的来水保证率分别为Pf=37.5%、Pk=62.5%,转化为累计频率P(xf)=0.625、P(xk)=0.375。基于上述划分,3个站点降雨变化的丰枯遭遇可以分丰枯同步、丰枯异步2个大情形下共27种情况,包括:同丰、同平、同枯、两丰一枯、两枯一丰、两枯一平、两平一枯、两平一丰、两丰一平,一丰一平一枯等。通过Gumbel-Hougaard Copula函数建立联合分布模型,计算27种情况的遭遇概率，见表7。

表7 降雨变化丰枯遭遇概率计算结果 %

就时间尺度看,汛期、非汛期、全年丰枯同步发生概率分别为45.8%、57.3%、51.4%;丰枯异步发生概率分别为54.2%、42.7%、48.6%。丰枯同步组合发生概率最大的是非汛期,达57.3%,明显高于这一时段丰枯异步组合的发生概率。这种情况对于非汛期降雨量较少的东江流域极为不利,应予以重视。汛期丰枯同步组合发生概率45.8%,低于丰枯异步;其中同丰组合发生概率23.1%,高于同枯组合发生概率18.9%,调水重点应放在洪水遭遇上,调节水库运行机制;年尺度上,丰枯同步、丰枯异步发生概率基本持平。总体看来,3个时段丰枯组合发生概率各不相同,流域内降雨丰枯遭遇存在时间上的变异性。

就制定流域内水资源优化配置方案,实现水资源可持续利用来讲,应更关心调水的利弊情况。3个时段非汛期丰枯同步发生概率最大,是流域内调水最不利的时期。非汛期调水不利情况发生总概率为65.8%,汛期为61.5%,全年调水不利总概率为64%。分析表明,就研究流域来说,调水不利情况偏多,需要决策者制定针对性政策。就水资源总量来说,3个时段同丰组合发生概率占整体比重最大,说明流域内水资源总量相对较丰富。

3.2 丰枯遭遇条件概率分析

为更好地制定流域内水资源优化配置方案,已知上游发生一定量级降雨情况时,需要预测中、下游发生不同量级降雨的概率值。Copula函数建立的联合分布模型同样为解决这一问题提供了有效的工具。当已知上游分别出现枯、平、丰水年时,中、下游发生不同级别来水的条件概率计算公式如下(篇幅限制这里只列出已知上游来水情况,中、下游同枯的发生概率):

已知上游龙川站为枯水年,中、下游河源、博罗站为枯水年的发生概率:

F(y,z|x)=P(Y≤yk,

(10)

已知上游龙川站为平水年,中、下游河源、博罗站为枯水年的发生概率:

F(y,z|x)=P(Y≤yk,Z≤zk|xk≤x≤xp)=

(11)

已知上游龙川站为丰水年,中、下游河源、博罗站为枯水年的发生概率:

F(y,z|x)=P(Y≤yk,Z≤zk|x≥xf)=

(12)

图4为汛期、非汛期、全年上游龙川站为枯水情况时,中、下游河源、博罗站发生不同量级降雨的条件概率分布。图4更直观地表现出了条件概率的大小,可以直接查出上游枯水情况,中、下游某一量级降雨对应的发生概率,如在年尺度下,已知上游枯水,中、下游2站同枯的发生概率P(Y≤yk,Z≤zk|X≤xk)=57.1%。对比3站同枯的发生概率P(X≤xk,Y≤yk,Z≤zk)=21.4%,增加了2.7倍。图5为不考虑上游降雨情况,中、下游枯水年的发生概率与已知上游枯水,中、下游枯水发生概率的对比。从图5可知,3个时段对比,已知上游来水情况,中、下游枯水发生概率变化最大的为非汛期,增加了2.4倍,年尺度次之,汛期变化幅度最小,约增加2倍。

图4 上游龙川站降雨量为枯水情况下,中、下游河源、博罗站不同量级降雨遭遇条件概率

图5 中、下游同枯事件发生概率与条件概率对比

4 结 论

在全球气候变化的大背景下,以流域内不同站点降雨事件相关性为出发点,利用Copula函数建立流域降雨事件多变量联合分布模型。通过拟合优度检验,最终选取Gumbel-Hougaard Copula函数构建了东江流域上、中、下游3个站点汛期、非汛期及全年降雨的联合分布,并在此基础上深入分析了3个站点多种情境下丰枯遭遇发生的概率及条件概率,结论如下:

a. 3站点降雨丰枯遭遇在时间尺度上存在一定的差异性。汛期降雨丰枯同步发生概率45.8%,明显小于丰枯异步概率,对调水有利的情况较易发生;而对于非汛期来说,丰枯同步发生概率57.3%,丰枯异步发生概率仅为42.7%,调水不利情况较多,水资源不足。针对降雨事件年内分配不均匀问题,应制定针对性的调水方案;年尺度来看,丰枯同步、丰枯异步发生概率相差不大,但调水不利情况发生概率达64%。

b. 汛期、非汛期及全年降雨3站点同丰概率分别为23.1%、27.3%和25.2%,相对于其他情形来说发生概率较大。表明,流域内调水,在满足用水要求的同时可能会有富余水量,要充分发挥流域内水库的调蓄作用,合理高效利用水资源。

建立上游为枯水情况,中、下游不同量级降雨组合发生概率的等值线图,以方便查取,为流域水资源合理配置提供实用参考。对比分析上游降雨情况对中、下游在不同尺度下降雨事件发生概率的综合影响大小,具有一定的理论与实践意义。

[1] JOE H.Multivariate models and multivariate dependence concepts[M].London:Chapman & Hall/crc,1997.

[2] NELSEN R B.An Introduction to Copulas[J].New York:Springer Publishing Company,2010.

[3] MICHELE C D,SALVADORI G.A Generalized Pareto intensity-duration model of storm rainfall exploiting 2-Copulas[J].Journal of Geophysical Research Atmospheres,2003,108(D2):171-181.

[4] 闫宝伟,郭生练,肖义.南水北调中线水源区与受水区降水丰枯遭遇研究[J].水利学报,2007,38(10):1178-1185.(YAN Baowei,GUO Shenglian,XIAO Yi.Synchronous-asynchronous encounter probability of rich-poor precipitation between water source area and water receiving areas in the middle route of South-to-North Water Transfer Project[J].Journal of Hydraulic Engineering,2007,38(10):1178-1185.(in Chinese))

[5] JENQ T S,SONG F,SARELEES N.Assessment of hydrological droughts for the Yellow River,China,using copulas[J].Hydrological Processes,2007,21(16):2157-2163.

[6] 谢华,罗强,黄介生.基于三维copula函数的多水文区丰枯遭遇分析[J].水科学进展,2012,23(2):186-193.(XIE Hua,LUO Qiang,HUANG Jiesheng.Synchronous asynchronous encounter analysis of multiple hydrologic regions based on 3 D copula function[J].Advances in Water Science,2008,19(4):505-511.(in Chinese))

[7] 冯平,牛军宜,张永,等.南水北调西线工程水源区河流与黄河的丰枯遭遇分析[J].水利学报,2010,41(8):900-907.(FENG Ping,NIU Junyi,ZHANG Yong,et al.Analysis of wetness-dryness encountering probability among water source rivers and the Yellow River in the Western Route of South-to-North Water Transfer Project[J].Journal of Hydraulic Engineering,2010,41(8):900-907.(in Chinese))

[8] SUBIMAL G.Modelling bivariate rainfall distribution and ghroenerating bivariate correlated rainfall data in neighbouring meteorological subdivisions using Copula[J].Hydrological Process,2010,24:3358-3567.

[9] ZHANG L,SINGH V P.Bivariate rainfall frequency distributions using Archimedean Copulas[J].Journal of Hydrology,2007,332:93-109.

[10] 武传号,黄国如,吴思远.基于Copula函数的广州市短历时暴雨与潮位组合风险分析[J].水力发电学报,2014,33(2):33-40.(WU Chuanhao,HUANG Guoru,WU Siyuan.Risk analysis of combinations of short duration rainstorm and tidal level in Guangzhou based on Copula function[J].Journal of Hydroelectric Engineering,2014,33(2):33-40.(in Chinese))

[11] 梁忠民,郭彦,胡义明,等.基于Copula函数的三峡水库预泄对鄱阳湖防洪影响分析[J].水科学进展,2012,23(4):485-492.(LIANG Zhongmin,GUO Yan,HU Yiming,et al.Impact of the pre-release from Three Gorges Reservoir on flood control in Poyang Lake using a Copula-based approach[J].Advances in Water Science,2012,23(4):485-492.(in Chinese))

[12] ZHANG L,SINGH V P.Bivariate flood frequency analysis using the copula method[J].Journal Hydrologic Engineering ASCE,2006,11(2):150-164.

[13] 冯平,李新.基于Copula函数的非一致性洪水峰量联合分析[J].水利学报,2013,44(10):1137-1147.(FENG Ping,LI Xin.Bivariate frequency amalysis of non-stationary flood time series based on Copula methods[J].Journal of Hydraulic Engineering,2013,44(10):1137-1147.(in Chinese))

[14] 李小奇,郑东健,鞠宜朋.基于Copula熵理论的大坝渗流统计模型因子优选[J].河海大学学报(自然科学版),2016,44(4):370-376.(LI Xiaoqi,ZHENG Dongjian,JU Yipeng.Input factor optimization study of dam seepage statistical model based on copula entropy theory[J].Journal of Hohai University(Natural Sciences),2016,44(4):370-376.(in Chinese))

[15] 刘永定,吴对林,李美敏,等.东江东莞段水污染现状与防治对策[J].东莞理工学院学报,2011,18(5):6-9.(LIU Yongding,WU Duilin,LI Meimin,et al.Pollution situation of Dongguan Reaches of Dongjiang River and its relevant countermeasures[J].Journal of Dongguan University of Technology,2011,18(5):6-9.(in Chinese))

[16] 钟波,张鹏.Copula选择方法[J].重庆工学院学报(自然科学版),2009,23(5):155-160.(ZHONG Bo,ZHANG Peng.Research on the methods to choose Copula[J].Journal of Chongqing Institute of Technology(Natural Science),2009,23(5):155-160.(in Chinese))