复杂断层矿区地下水三维数值模拟

朱 君,安瑞瑞

(1.中国辐射防护研究院,山西 太原 030006; 2.山西晋环科源环境资源科技有限公司,山西 太原 030024)

随着地下水数值模拟技术的发展,应用该技术反映矿区地下水动态变化已是目前最常用的方法,国际上通用的商业软件有Visual Modflow、GMS、FEMWATER、FEFLOW等。如何提高数值模拟的精准度使之更加符合实际情况是亟待解决的问题。矿区断层构造复杂,有的区域甚至纵横交错,断层的概化和处理成为影响模拟结果的一个重要因素。目前,国内在地下水数值模拟中能概化三维断层并应用到模型中的实例很少,普遍的做法是将断层两侧地层的渗透系数分区取值,或者与相邻含水层视为一个系统。而考虑断层因素的情况也是应用Visual Modflow、GMS针对单断层的简单构造区,Visual Modflow和GMS采用有限差分法,缺点是网格剖分方向必须与断层走向一致,见图1中的Fa、Fb；否则概化断层的网格呈“锯齿”状,见图1中的Fc,影响计算结果的收敛性和精度,显然在复杂断层区域采用有限差分法已无法满足精度要求[1-5]。FEMWATER和FEFLOW采用有限节点法,能够消除“锯齿”状网格的不利影响,更好地描述复杂的断层构造,模拟计算结果更加真实[6-8]。国外应用FEFLOW在地下水模型中对复杂断层的概化已经能够做得非常精准,因此国内亟须弥补差距[9-13]。本文以内蒙古某煤矿内的10条断层为例,建立复杂断层区的地下水三维数值模型。

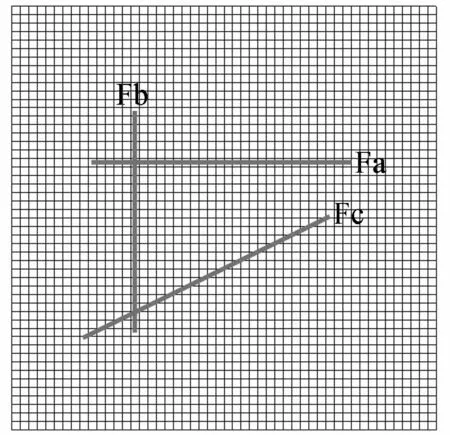
图1 有限差分法断层概化示意图

1 研究区概况

1.1 基本情况

研究矿区位于内蒙古自治区与宁夏回族自治区交界处,属于华北地台、鄂尔多斯盆地西缘褶皱冲断带的北段,即贺兰山—横山段。褶皱、断裂较发育,褶皱轴向及主要断裂多呈近南北向展布,其次为北东—北东东向断裂及北西向断裂。总体构造形态为受断层切割的单斜,地层总体东倾,走向近南北,在单斜基础上发育次级褶曲和少量断层。

1.2 构造特征

矿区内共有10条断层,其中逆断层6条(F1、F2、F3、F5、F6、F8),正断层4条(F4、F7、F9、F10),均属于倾斜断层,错断了新近系以下地层,断层特征见表1。

表1 断层特征

1.3 水文地质条件

矿区开采煤层位于二叠系山西组,上覆含水层从上至下为第四系松散孔隙含水层,厚2.05～59.50 m,主要以大气降水补给,受下伏新近系黏土隔水层控制,厚度82.60～397.32 m,由东北向西南径流。新近系下部砂砾石层含水层,厚度5.45～60.48 m,平均厚19.78 m,孔隙发育,透水性好,为该地区富水性最佳的含水层,主要接受区域侧向补给,由西北向东南径流。二叠系石盒子组砂岩裂隙含水层,厚128.06～638.76 m,主要接受上覆新近系砂砾石层含水层补给,由西北向东南径流。二叠系山西组砂岩裂隙含水层,厚24.42～121.69 m,主要接受上覆新近系砂砾石层含水层越流补给和二叠系石盒子组砂岩裂隙含水层直接补给,由西北向东南径流。因此二叠系砂岩裂隙含水层与新近系砂砾石层含水层地下水有着相同的变化规律。

2 地下水数值模拟

2.1 模拟区及边界条件

模型的东边界(AB段),以葱沟断层为界,概化为流量边界。模型的北边界(AD段)、南边界(BC段),大致以地下水流线为界,概化为流量边界。模型的西边界(CD段),以已知水头为界,概化为定水头边界。模拟区面积约130 km2,基本概况见图2。

图2 模拟区基本概况示意图

2.2 目标含水层概化

开采煤层上覆4含水层,分别为第四系松散孔隙含水层、新近系砂砾石含水层、二叠系石盒子组砂岩裂隙含水层和二叠系山西组砂岩裂隙含水层。另外第四系松散孔隙含水层与新近系砂砾石含水层之间有82.60～397.32 m的黏土层,可视为弱透水层,因此整个模拟区自上而下划分为5层(表2)。

表2 目标含水层概化情况

2.3 断层概化

矿区内的10条断层均属于倾斜断层,倾角在70°～75°之间,纵横交错,较为复杂,故将倾斜断层处理为垂直断层。空间离散时,垂向上分为5层,断层处网格加密,共生成三角网格370 060个,节点217 537个。网络剖分示意图见图3,断层概化三维示意图见图4。

图5 各含水层抽水历时曲线

图3 网格剖分示意图

图4 断层概化三维示意图

2.4 水文地质参数

水文地质参数的取值,包括含水层、弱透水层、断层x、y、z方向的主渗透系数Kxx、Kyy、Kzz、弹性释水系数Sy、单位贮存量Ss。渗透系数的取值主要是参考矿区及相邻矿区的抽水试验资料,抽水历时曲线见图5,图中S为水位降深,Q为流量,得到第四系松散孔隙含水层、新近系砂砾石含水层、二叠系石盒子组砂岩裂隙含水层、二叠系山西组砂岩裂隙含水层水平方向的渗透系数Kxx、Kyy,垂直方向的渗透系数Kzz一般为水平方向渗透系数的1/10[9-12]。另外,根据矿区《水文地质勘查成果报告》,断层透水,渗透系数约为相邻含水层的10倍,经模型校核后确定该参数取值。弹性释水系数Sy、单位贮存量Ss主要取经验值。另外,第四系松散孔隙含水层根据水文地质参数不同分为A、B 2个区。具体取值情况见图6和表3。

图6 第四系松散孔隙含水层水文地质参数分区

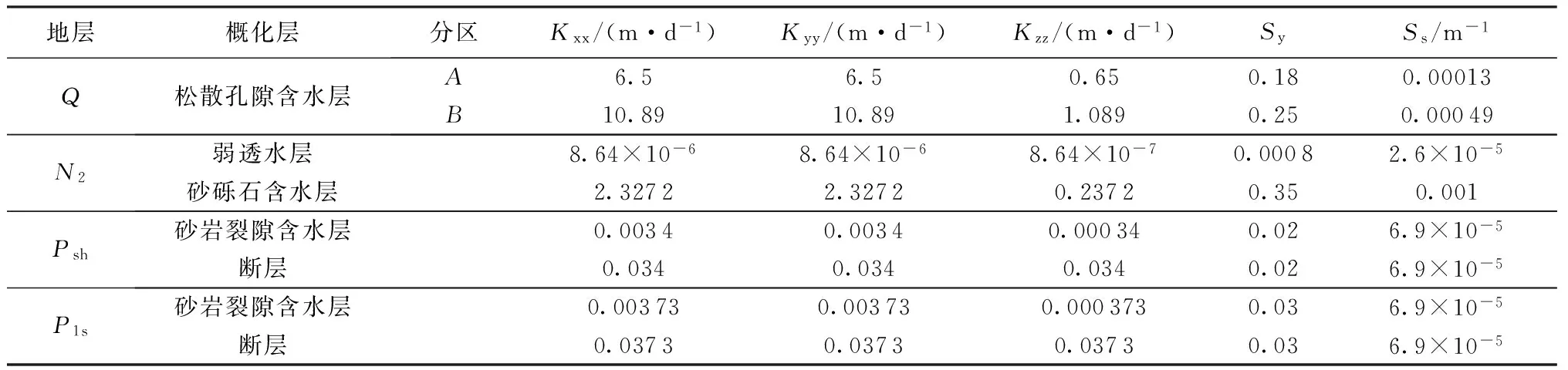
地层概化层分区Kxx/(m·d-1)Kyy/(m·d-1)Kzz/(m·d-1)SySs/m-1Q松散孔隙含水层A6.56.50.650.180.00013B10.8910.891.0890.250.00049N2弱透水层8.64×10-68.64×10-68.64×10-70.00082.6×10-5砂砾石含水层2.32722.32720.23720.350.001Psh砂岩裂隙含水层0.00340.00340.000340.026.9×10-5断层0.0340.0340.0340.026.9×10-5P1s砂岩裂隙含水层0.003730.003730.0003730.036.9×10-5断层0.03730.03730.03730.036.9×10-5

2.5 模型识别与验证

模拟区内共有12个第四系松散孔隙含水层地下水水位监测点,其位置分布见图2。在2014年8月—2015年3月的一个连续水文年对该含水层的水位进行了监测,具体监测值见表4,从监测结果分析,在一个连续水文年中,所有点位水位变化幅度在0.56～0.61 m,可视为稳定流,将3期水位的平均值作为模型校核资料。

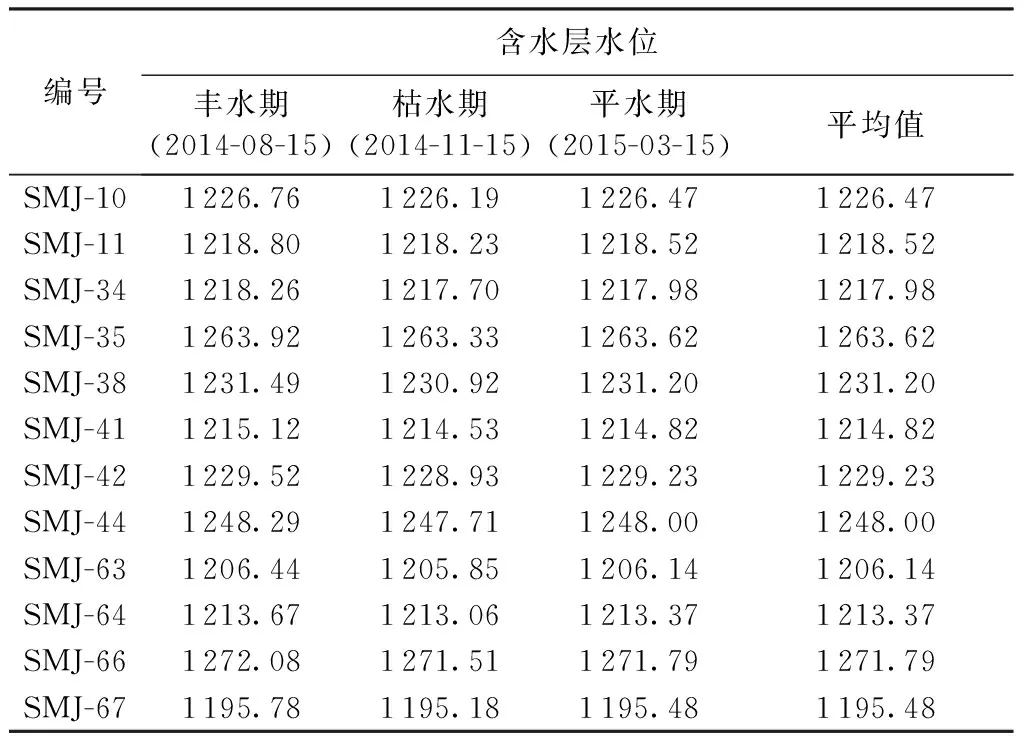
表4 第四系松散孔隙含水层水位监测值 m

图7 第四系松散孔隙含水层水位拟合线

图8 二叠系石盒子组砂岩裂隙含水层水位拟合线

模型建立后,对比计算水位与监测水位的吻合程度(图7～8),验证模型的合理性和准确性。在加入疏干排水条件前,以稳定流模式运行模型,计算得到第四系松散孔隙含水层的初始水位分布值。该地区年平均降雨量为270.4 mm,降雨入渗系数经过模型验证和校核后取0.12,输入模型的降雨入渗量为32.85 mm/d。通过稳定流模型计算得到第四系松散孔隙含水层初始水位与实际监测水位的偏差范围在0.39～1.83 m,其中偏差较大的有3处,分别是SMJ-11为1.69 m,SMJ-35为1.83 m,SMJ-44为1.74 m。其余监测点的偏差均小于0.72 m(表5)。

表5 拟合结果 m

表6 二叠系石盒子组砂岩裂隙含水层监测水位与计算水位 m

表7 二叠系山西组砂岩裂隙含水层和新近系砂砾石含水层之间的水位关系

另外根据《水文地质勘查成果报告》,矿区有9个水文地质钻孔监测过二叠系石盒子组砂岩裂隙含水层水位(表6);2个水文地质钻孔监测过二叠系山西组砂岩裂隙含水层和新近系砂砾石含水层之间的水位关系(表7)。由钻孔ZK2803、ZK2805可知,新近系砂砾石含水层(E)、二叠系山西组砂岩裂隙含水层(P1s)水位相差不大,间接说明新近系砂砾石层含水层以下地层没有稳定隔水层,二叠系石盒子组砂岩裂隙含水层和二叠系山西组砂岩裂隙含水层主要靠新近系砂砾石含水层补给,地下水有着相同的变化规律。

二叠系石盒子组砂岩裂隙含水层初始水位与实际监测水位的偏差范围在0.33～2.51 m,根据以上2含水层水位拟合程度可知,建立的模型和水文地质参数的取值基本上能够反映实际情况。第四系松散孔隙含水层计算水位等值线图和二叠系石盒子组砂岩裂隙含水层计算水位等值线见图9～10。

图9 第四系松散孔隙含水层计算水位等值线

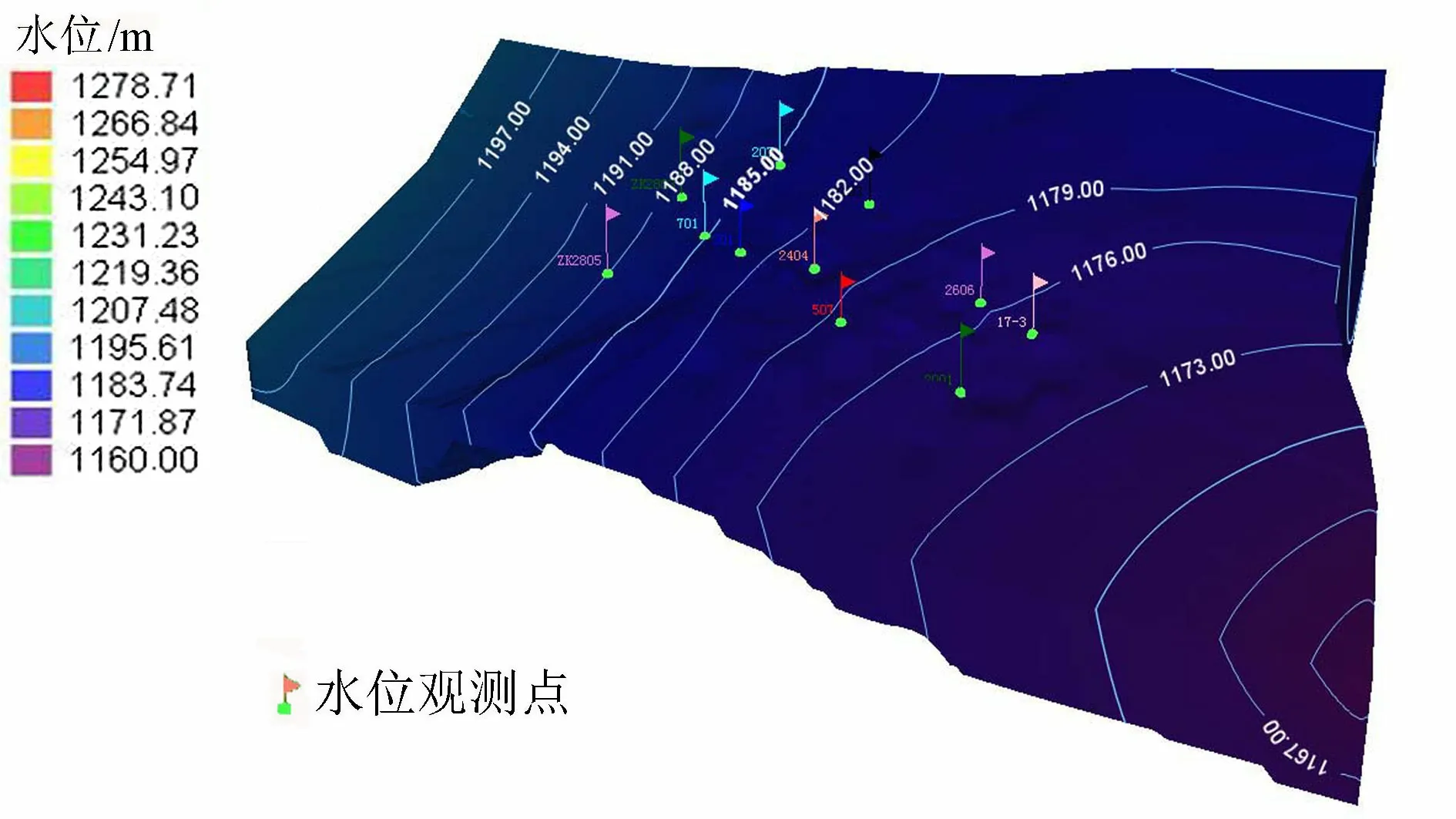
图10 二叠系石盒子组砂岩裂隙含水层计算水位等值线

2.6 计算结果

根据冒落裂隙带和导水裂隙带计算,在煤层隐伏露头处附近最大高度能导通新近系底部砂砾石含水层,矿区开采后正常涌水量为13 800 m3/d,垂向上地下水流速度加剧,将涌水量分采区、分时段输入模型,并以非稳定流模型计算矿区开采30年后对地下水资源的影响,得到矿区开采30年水位等值线见图11。预测结果显示,开采后水位变化部分集中在新近系砂砾石含水层及以下区域,第四系松散孔隙含水层的水位等值线基本上没有变化,分析原因是第四系松散孔隙含水层底部有厚度82.60～397.32 m的完整且连续的棕红色黏土层,有效阻隔了地下水的渗漏和越流,对该含水层影响较小。

图11 矿区开采30年后水位等值线

矿区开采30年后,二叠系山西组砂岩裂隙含水层、二叠系石盒子组砂岩裂隙含水层、新近系砂砾石含水层形成以开采区为中心的降落漏斗,最大降深及影响面积详见表8。分析原因是二叠系山西组煤层开采后,“两带”直接破坏二叠系山西组砂岩裂隙含水层、二叠系石盒子组砂岩裂隙含水层下部以及煤层露头处的新近系底部砂砾石含水层,加大了地下水的渗漏和越流。另外矿区内的10条透水断层,形成渗水通道,加剧了上述含水层地下水的下渗。

表8 含水层水位降深、影响面积

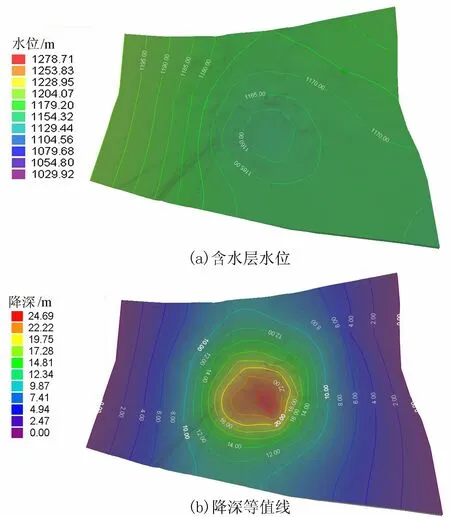
图12 开采30年后新近系砂砾石含水层水位及降深等值线

从预测结果来看(图12～14),二叠系石盒子组砂岩裂隙含水层与新近系砂砾石含水层的水位及水位降深等值线基本相似。原因是该地区二叠系石盒子组砂岩裂隙含水层主要接受上覆新近系砂砾石层含水层补给,且两含水层之间没有隔水层,因此地下水有着相同的变化规律。

图13 开采30年后二叠系石盒子组砂岩裂隙含水层水位及降深等值线

图14 开采30年后二叠系山西组砂岩裂隙含水层水位及降深等值线

3 结 论

复杂断层的概化和处理方式是影响数值模拟结果的重要因素,本文以内蒙古某矿区中的10条错综复杂的断层为研究对象,应用FEFLOW软件将倾斜断层简化为垂直透水断层,建立三维地下水数值模型,克服了以往Visual Modflow、GMS建模过程中断层处“锯齿”状网格对计算结果收敛性和精度的影响,并预测了矿区开采30年后,对上覆各含水层地下水资源的破坏程度,二叠系山西组砂岩裂隙含水层、二叠系石盒子组砂岩裂隙含水层、新近系砂砾石含水层受到了不同程度的影响,而第四系松散孔隙含水层由于底部较厚且完整、连续的黏土层阻隔几乎没有受到影响。

[1] 王博,刘耀炜,孙小龙,等.断层对地下水渗流场特征影响的数值模拟[J].地震,2008,28(3):115-123.(WANG Bo,LIU Yaowei,SUN Xiaolong,et al.Numerical simulation of the influence of fault on the groundwater seepage field[J].Journal of Earthquake,2008,28(3):115-123.(in Chinese))

[2] 梁世川,徐明,王磊,等.GMS在地下水数值模拟及断层处理中的应用：以盖孜河水源地为例[J].地下水,2013,35(6):53-54,125.(LIANG Shichuan,XU Ming,WANG Lei,et al.Application of GMS in numerical simulation of groundwater and fault generalizability: as an example for the water source location of Gez river[J].Ground Water,2013,35(6):53-54,125.(in Chinese))

[3] 武强,朱斌,徐华,等.MODFLOW在淮北地下水数值模拟中的应用[J].辽宁工程技术大学学报(自然科学版),2005,24(4):500-503.(WU Qiang,ZHU Bin,XU Hua,et al.Application of MODFLOW in groundwater numerical simulation in Huaibei City[J].Journal of Liaoning Technical University (Natural Science),2005,24(4):500-503.(in Chinese))

[4] 牛建立.地下水数值计算中断层处理的“切割—导通法”[J].煤田地质与勘探,2002,30(5):39-40.(NIU Jianli.Cutting-conduction method for fault generalizability in groundwater numerical calculation[J].Coal Geology & Exploration,2002,30(5):39-40.(in Chinese))

[5] 朱斌,武强.断层影响下的地下水流数值模拟[J].桂林理工大学学报,2005,25(1):31-35.(ZHU Bin,WU Qiang.Numerical simulation of groundwater flow under the influence of faults[J].Journal of Guilin University of Technology,2005,25(1):31-35.(in Chinese))

[6] 殷晓曦,陈陆望,林曼利,等.采动影响下任楼煤矿地下水流三维数值模拟[J].合肥工业大学学报(自然科学版),2013,36(1):93-98.(YIN Xiaoxi,CHEN Luwang,LIN Manli,et al.Three-dimensional numerical simulation of groundwater flow in Renlou Mine under mining disturbance[J].Journal of Hefei University of Technology(Natural Science),2013,36(1):93-98.(in Chinese))

[7] 韩巍,李国敏,黎明,等.大武水源地岩溶地下水开采动态数值模拟分析[J].中国岩溶,2008,27(2):182-188.(HAN Wei,LI Guomin,LI Ming,et al.Dynamic numerical simulation of groundwater in Dawu karst water source location[J].Carsologica Sinica,2008,27(2):182-188.(in Chinese))

[8] 刘志峰,柳硕林,王琳琳,等.数值模拟法在西龙河峄山断层带岩溶水允许开采量评价中的应用[J].地质学刊,2010,34(3):271-274.(LIU Zhifeng,LIU Shuolin,WANG Linlin,et al.The application of numerical simulation method to evaluation the allowable exploitation amount of cavern water in Xilong River Yishan fault zone[J].Journal of Geology,2010,34(3):271-274.(in Chinese))

[11]LUO J.Hydrogeological model Jura Os[R].Bern:Arbeitsbericht NAB 13-26,2014.