022Cr17Ni12Mo2不锈钢缺口试样的疲劳寿命预测

吴启舟，李江华，缑之飞，金 丹

(沈阳化工大学能源与动力工程学院， 沈阳 110142)



022Cr17Ni12Mo2不锈钢缺口试样的疲劳寿命预测

吴启舟，李江华，缑之飞，金 丹

(沈阳化工大学能源与动力工程学院， 沈阳 110142)

摘要：对022Cr17Ni12Mo2不锈钢光滑和缺口试样进行了拉伸试验及应力控制的低周疲劳试验，并采用Neuber律、Peterson方法和基于试验结果计算的疲劳缺口系数进行了疲劳寿命预测。结果表明：022Cr17Ni12Mo2不锈钢具有明显的缺口效应和良好的塑性，缺口效应在低应力水平下更为明显；在不同应力水平下不锈钢均表现出了循环硬化现象，且随着应力幅值的增加其循环硬化更为明显；Neuber律和Peterson方法得到的疲劳寿命预测结果均偏于保守，基于试验结果的疲劳寿命预测结果更准确。

关键词：022Cr17Ni12Mo2不锈钢；低周疲劳；缺口试样；疲劳寿命预测

0引言

在实际工程结构中不可避免地存在着键槽、螺纹孔等缺陷(统称为缺口)，从而带来明显的应力集中，疲劳裂纹往往在此处萌生，缺口件疲劳性能研究正日益引起各国学者的重视。022Cr17Ni12Mo2不锈钢(对应美国牌号316L)具有优异的高温强度,良好的加工硬化、塑性、焊接性、耐腐蚀性等综合性能，被广泛应用于造船以及石油化工等行业。

目前，针对316L不锈钢光滑件的疲劳性能已开展了一定的研究。Roy等[1-2]通过常温单轴低周疲劳试验及显微组织分析发现，316L不锈钢在循环初期表现为循环硬化，随后软化、饱和直至失效；Kim等[3-4]对316L和316LN不锈钢进行了疲劳试验，得出疲劳寿命、蠕变疲劳寿命以及峰值应力随氮含量增加而增大的结论；有限元分析为研究材料疲劳性能提供了一个新的途径，蒋春松等[5]利用ABAQUS软件对316L不锈钢构件的弯曲微动过程进行了有限元模拟计算，采用多轴疲劳准则Smith-Watson-Topper(SWT)参数模型预测了弯曲微动裂纹萌生的位置和构件的疲劳寿命。已有的316L不锈钢的疲劳性能研究大都局限于光滑试样，有关缺口对其疲劳性能的影响研究相对较少，且集中在缺口对疲劳裂纹扩展行为影响的研究方面[6]。

为此，作者针对022Cr17Ni12Mo2不锈钢光滑和缺口试样进行了拉伸试验和应力比为0的应力控制低周疲劳试验，得到了不同应力水平下的应力-寿命曲线，并采用Neuber律、Peterson方法和基于试验得到的疲劳缺口系数Kf计算损伤参量，进行缺口试样疲劳寿命预测。

1试样制备与试验方法

1.1　试样制备

试验材料为太钢不锈钢股份有限公司生产的022Cr17Ni12Mo2不锈钢，其化学成分如表1所示，热处理状态为冷轧态，屈服强度σs为342 MPa，抗拉强度σb为607 MPa，断面收缩率ψ为68%，弹性模量E为200 GPa。

在不锈钢板上截取光滑试样和缺口试样，其形状和尺寸见图1，厚度为1 mm。缺口试样的理论应力集中系数Kt为2.4。

1.2　试验方法

根据GB/T 228-2002，在EUT-1020型疲劳试验机上进行光滑和缺口试样的室温拉伸试验，加载速度为0.008 kN·s-1，做2组试验取平均值；随后根据GB/T 15248-2008，对光滑和缺口试样进行相同条件下应力控制的拉-拉疲劳试验，波形为三角波，周期4 s，设置最小载荷为0 kN(即应力比R为0)，最大载荷分别为1.4，1.3，1.2，1.1，1.0，0.9，0.8，0.7 kN，以试样断裂作为疲劳失效依据，记录最大循环周次，以此作为疲劳寿命。试验参数及结果如表2所示。

表1　试验钢的化学成分(质量分数)Tab.1　Chemical composition of experimental steel (mass)　%

图1　不同试样的形状和尺寸Fig.1　Shapes and dimensions of smooth (a) and notched (b) specimens

表2　光滑和缺口试样的试验参数及试验结果Tab.2　Experimental parameters and results of smoothand notched specimens

2试验结果与讨论

2.1　拉伸性能

由图2可见，缺口试样的屈服强度和抗拉强度分别为360 MPa和632 MPa，而光滑试样的分别为335 MPa和598 MPa，可见由于受到缺口效应的影响，出现了缺口强化，使得缺口试样的屈服强度和抗拉强度均高于光滑试样的；在应力-应变曲线后期，应力均随应变的增加而下降，试样在断裂前均出现了颈缩现象，说明022Cr17Ni12Mo2不锈钢具有良好的塑性。

图2　不同试样的工程应力-应变曲线Fig.2　Engineering stress-strain curve for notched specimen

2.2　拉-拉疲劳性能

2.2.1S-N曲线

从图3中可以看到，光滑和缺口试样的S-N曲线并不平行，可见不同应力水平下缺口效应并不相同。材料在交变载荷作用下，会发生疲劳裂纹的萌生和扩展，直至断裂；在较高循环应力作用下，材料的疲劳寿命较低，裂纹扩展寿命占总寿命比例较大。022Cr17Ni12Mo2不锈钢的塑性较好，在高的交变应力作用下，缺口根部会产生明显的塑性变形，导致应力重新分布，因此应力集中的影响相对减小，表现为在高应力水平下两种试样的S-N曲线有相交的趋势；而在较低的交变应力作用下，缺口效应明显，疲劳寿命降低显著，疲劳强度因子较大，这一结论与文献[7]的相一致。

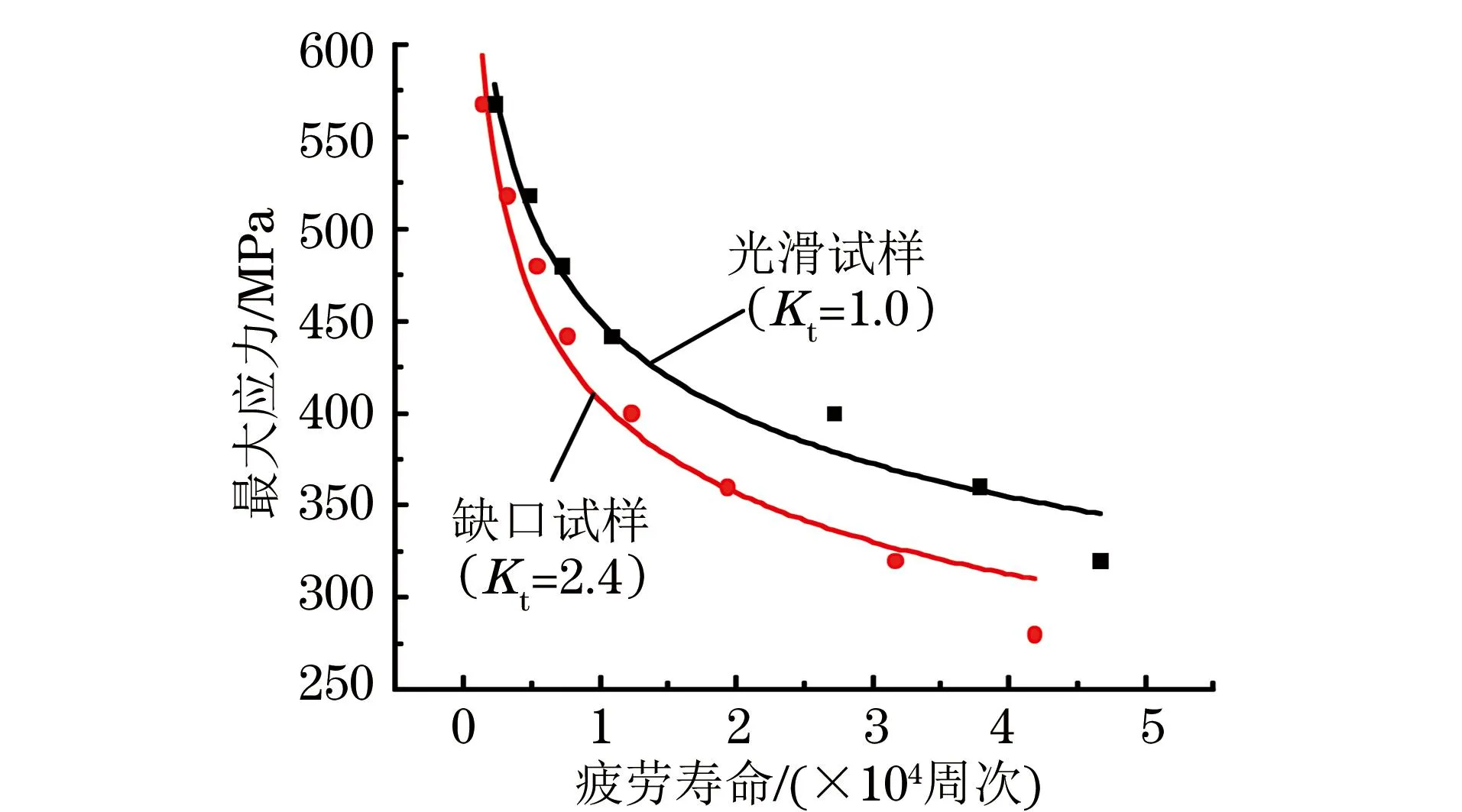
图3　光滑试样和缺口试样S-N曲线Fig.3　S-N curves of smooth and notched specimens

光滑试样S-N曲线拟合公式如下：

(1)

式中：σmax为最大循环应力；Nf为疲劳寿命。

缺口试样S-N曲线拟合公式如下：

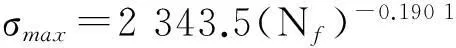
(2)

用式(1)除以式(2)得到缺口试样疲劳强度因子与疲劳寿命的关系式为:

(3)

式中：K′为缺口试样疲劳强度因子。

由式(3)拟合得到的曲线如图4所示。由图4可以看到，缺口试样的疲劳强度因子随着疲劳寿命的增加而增大。

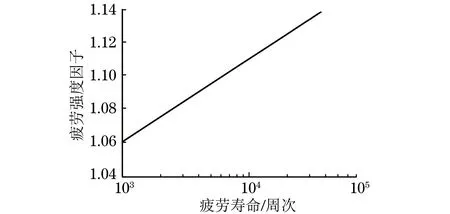
图4　缺口试样疲劳强度因子与疲劳寿命的关系Fig.4　Relation between fatigue strength factor and fatigue lifeof notched specimen

2.2.2循环硬化特性

由图5可知，在三种交变应力作用下缺口试样的应变均先随着循环次数的增加而减小，表现出循环硬化的特性；当循环60周次时应变达到稳定。在0～320 MPa交变应力作用下，循环硬化的应变范围Δε为0.017 6%；当交变应力为0～360 MPa时，Δε为0.019 3%；0～442 MPa时，Δε为0.024 0%。可见,随着交变应力增大，其由初始的循环硬化达到循环稳定时的应变范围增大，说明循环硬化更明显。

图5　缺口试样应变-循环次数曲线Fig.5　Strain vs number of cycles for notched specimens

3疲劳寿命预测

3.1　损伤计算方法

在局部应力-应变分析中，Neuber律[8]以其简单性被工程界广泛应用，表达式为：

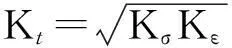
(4)

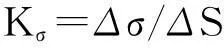
(5)

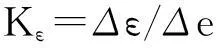
(6)

式中：Kt为理论应力集中系数；ΔS，Δe分别为名义应力和名义应变；Δσ和Δε分别为应力集中处的局部应力和局部应变。

结合Ramberg-Osgood方程，即可确定缺口根部的局部应力和应变范围：

(7)

式中:n′为循环硬化指数;K为循环硬化系数;E为材料弹性模量。

Neuber律在使用过程中通常会得到偏于安全的预测结果，采用疲劳缺口系数Kf代替Kt，得到修正Neuber律：

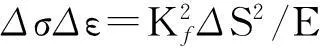
(8)

计算Kf的方法较多，作者采用了Peterson公式[9]：

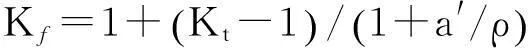
(9)

(10)

式中：ρ为缺口半径；a′为与拉伸应力值相关的材料常数；σb为材料的抗拉强度。

由式(9)计算得到疲劳缺口系数为1.7。

疲劳缺口系数被定义为疲劳试验中光滑试样与缺口试样的疲劳极限之比，结合试验结果及式(1)和(2)，将105周次作为试验钢的无限疲劳寿命[10]，得到光滑试样和缺口试样的疲劳极限值之比,即试验得到的疲劳缺口系数为1.2。

3.2　疲劳寿命预测

考虑缺口局部平均应力影响，采用基于应力疲劳的Manson-Coffin公式[11]：

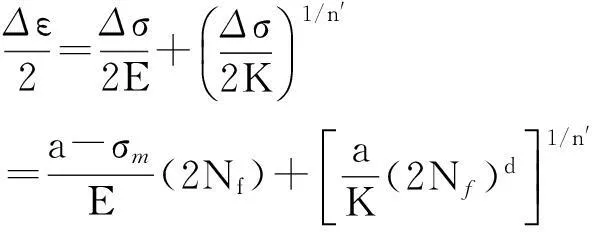
(11)

式中：σm为平均应力；K取2 850 MPa；n′取0.38;a和d为疲劳相关参数，分别为1 234.2 MPa和-0.17。

由于试验条件有限，试验中只获得了疲劳失效寿命。基于文献[12-13]，可认为022Cr17Ni12Mo2不锈钢缺口试样的裂纹萌生寿命约为总寿命的62%。

根据计算和试验的Kf进行损伤参量计算，结合式(11)对疲劳寿命进行预测，结果如图6所示，可见，Neuber律的预测结果普遍偏低。022Cr17Ni12Mo2不锈钢具有良好的塑性，缺口效应对疲劳寿命的降低程度较小，因此采用理论应力集中系数计算缺口处的应力、应变值必然高估了疲劳损伤程度；采用Peterson方法的预测结果较Neuber律的有所改善，但预测结果偏于保守的趋势依然存在；采用试验确定的Kf预测的疲劳寿命比Peterson方法的更准确，其预测结果均位于两倍分散带内。

图6　三种方法下疲劳寿命的预测结果Fig.6　Life prediction results by the three methods

4结论

(1) 022Cr17Ni12Mo2不锈钢缺口试样在拉伸试验中表现出了明显的缺口效应，缺口使得试样的强度提高，不锈钢具有良好的塑性。

(2) 在低交变应力循环下缺口效应对022Cr17Ni12Mo2不锈钢疲劳寿命的影响更为明显；在不同应力水平下，不锈钢均发生了循环硬化，且随着载荷幅值的增加，循环硬化程度增大。

(3) 采用Neuber律得到的疲劳寿命预测结果过于保守，Peterson方法的预测结果相对于Neuber律的有所改善，但结果仍偏于保守；采用试验所得疲劳缺口系数进行寿命预测，得到了比Peterson方法更为准确的结果，预测结果均位于两倍分散带内。

参考文献：

[1]ROY S C, GOYAL S, SANDHYA R, et al. Analysis of hysteresis loops of 316L(N) stainless steel under low cycle fatigue loading conditions[J]. Procedia Engineering, 2013,55: 165-170.

[2]ROY S C, GOYAL S,SANDHYA R, et al. Low cycle fatigue life prediction of 316L(N) stainless steel based on cyclic elasto-plastic response[J]. Nuclear Engineering and Design, 2012,253:219-225.

[3]KIM D W, CHANG J H, RYU W S.Evaluation of the creep-fatigue damage mechanism of type 316L and type 316LN stainless steel[J]. International Journal of Pressure Vessels and Piping, 2008,85(6): 378-384.

[4]KIM J W, BYUN T S. Analysis of tensile deformation and failure in austenitic stainless steels: Part I-temperature dependence[J]. Journal of Nuclear Materials,2010,396(1):1-9.

[5]蒋春松,彭金方,沈明学,等.316L不锈钢构件弯曲微动的有限元模拟及其疲劳寿命预测[J].机械工程材料, 2013,37(8):80-84.

[6]冯刚,宫大为,张朝阁,等.316L不锈钢的疲劳裂纹扩展行为试验[J].钢铁, 2014,49(6):74-78.

[7]虞忠良,赵永庆,周廉,等.TC21合金315 ℃高周疲劳光滑和缺口试样断口分析[J].材料工程, 2007(7):55-58.

[8]NEUBER H. Theory of stress concentration for shear-strained prismatic bodies with arbitrary nonlinear stress-strain law[J]. Journal of Applied Mechanics, 1961,28(4): 544-550.

[9]PETERSON R E. Notch Sensitivity[M]∥SINES G, WAISMAN J L. Metal Fatigue. New York: McGraw Hill, 1959: 293-306.

[10]李源,韩旭,刘杰,等.一种基于耗散能计算的高周疲劳参数预测方法[J].力学学报, 2013,45(3):367-373.

[11]张国栋,苏彬,王泓,等.K403合金高温低周应变疲劳寿命预测方法研究[J].机械强度, 2004,26(S1):263-266.

[12]SONG P S, SHIEH Y L. Stop drilling procedure for fatigue life improvement[J]. International Journal of Fatigue, 2004,26(12):1333-1339.

[13]金丹,田大将,王巍,等.非比例载荷下缺口件疲劳寿命预测[J].工程力学, 2014,31(10):212-215,221.

Fatigue Life Prediction of Notched Specimen for 022Cr17Ni12Mo2 Stainless Steel

WU Qi-zhou, LI Jiang-hua, GOU Zhi-fei, JIN Dan

(School of Energy and Power Engineering, Shenyang University of Chemical Technology, Shenyang 110142, China)

Abstract:The tensile tests and low cycle fatigue tests controlled by stress were conducted for smooth and notched specimens of 022Cr17Ni12Mo2 stainless steel. The fatigue notch factor obtained by Neuber′s rule, Peterson′s approach and the test results respectively was used to predict the fatigue life. The results show that the stainless steel presented an obvious notch effect and excellent ductility, and the notch effect was more obvious at lower stress level. The cyclic hardening phenomenon was observed at different stress levels and become more and more obvious with the increase of stress amplitude. The prediction results of fatigue life from Neuber′s rule and Peterson′s approach were both conservative, and that based on the test results was more accurate.

Key words:022Cr17Ni12Mo2 stainless steel; low cycle fatigue; notched specimen; fatigue life prediction

通讯作者(导师)：王砚军教授 (导师)：何宇廷教授

作者简介：韩田田(1990-)，女，山东济南人，硕士研究生。 张浩宇(1993-)，男，山西忻州人，硕士研究生。

基金项目：国家自然科学基金资助项目(51275208) 国家自然科学基金资助项目(51475470)

收稿日期:2015-03-20； 2015-06-19；

修订日期:2015-09-25 2015-10-05

DOI:10.11973/jxgccl201512015 10.11973/jxgccl201512014

中图分类号：TH142.2；TG174.3

文献标志码：A

文章编号：1000-3738(2015)12-0055-04