河道流动水体三维仿真方法研究
余 伟1,王 伟1,蒲慧龙2,王 鹏3
(1. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079; 2. 四川省第三测绘工程院,
四川 成都 610500; 3. 武汉吉嘉伟业科技发展有限公司,湖北 武汉 430079)
YUWei,WANGWei,PUHuilong,WANGPeng
河道流动水体三维仿真方法研究
余伟1,王伟1,蒲慧龙2,王鹏3
(1. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079; 2. 四川省第三测绘工程院,
四川 成都 610500; 3. 武汉吉嘉伟业科技发展有限公司,湖北 武汉 430079)
A3DSimulationMethodofFlowingRiverWater
YUWei,WANGWei,PUHuilong,WANGPeng
摘要:为满足水文观测数据的实时分析与应用需求,提出了一种不规则河道内流动水体仿真的方法。该方法重点研究了利用实测河道水位线数据并结合真实河道DEM地形数据进行河流边界线搜索及河面自动建模,构建多层水面叠加模型,利用流速驱动纹理块自适应于河道移动的动态纹理混合与渲染技术。在三峡库区水文仿真系统的实践中表明,该方法能够有效地模拟符合自然河道地形的动态流动水体,形象逼真地表现河面各处流速的差异化现象。
引文格式: 余伟,王伟,蒲慧龙,等. 河道流动水体三维仿真方法研究[J].测绘通报,2015(9):39-43.DOI:10.13474/j.cnki.11-2246.2015.0274
关键词:河流边界;水面自动建模;流动水体仿真;块状纹理;着色器
中图分类号:P208
文献标识码:B
文章编号:0494-0911(2015)09-0039-05
收稿日期:2014-09-01
基金项目:国家863计划(2013AA01A608);国家科技专项水专项(2013ZX07503001-06);国家火炬计划(2012GH722002)
作者简介:余伟(1989—),男,硕士生,研究方向为三维地理信息系统。E-mail:916702326@qq.com
一、引言
水体仿真对于流域治理、洪涝灾害预警分析等有着重要意义。近年来诸多利用GPU加速的河流水体仿真方法被提出[1-7],这些方法不仅效率高而且具有逼真的模拟效果。其中流动水体的动态仿真成为一个热难点,实际应用需求中流动水体仿真的逼真度不仅要求视觉上看起来十分真实,同时还要求模拟的水体能真实反映出水体的物理特性和运动规律[8]。杨在兴[9]等利用基于流畅的方法结合动态纹理映射技术真实地模拟出了河面流速等动态现象,但对于河流边界的搜索及水面自动建模未作讨论。冶运涛[10]等采用动态纹理映射技术实现了流动水体的动态模拟,但未对河道断面线的自动处理、自动加密等进行探讨,并且其纹理的偏移速率不能真实反映河水的流速。针对目前流动水体仿真中自动建模及动态渲染过程中存在的这些问题,笔者重点探讨了利用实测河道断面水位数据自动加密断面线并自动搜索河流边界线以及构建符合自然河道地形的水面模型,利用实际流速驱动块状纹理自适应于河道移动来表达河面各处流速等问题。最后笔者以长江干流三峡库区上游至重庆段为例,在GaeaExplorer2.0平台上使用HLSL着色语言及DirectX9.0建立了流动水体三维仿真系统。
二、河流边界提取与流动水体渲染方法
考虑到初始断面线过于稀疏及河道转弯角等特征,为了逼真模拟出河面各处流速的差异化现象,本文对断面线的加密、边界提取及流动水体的动态渲染采用如图1所示的流程进行。
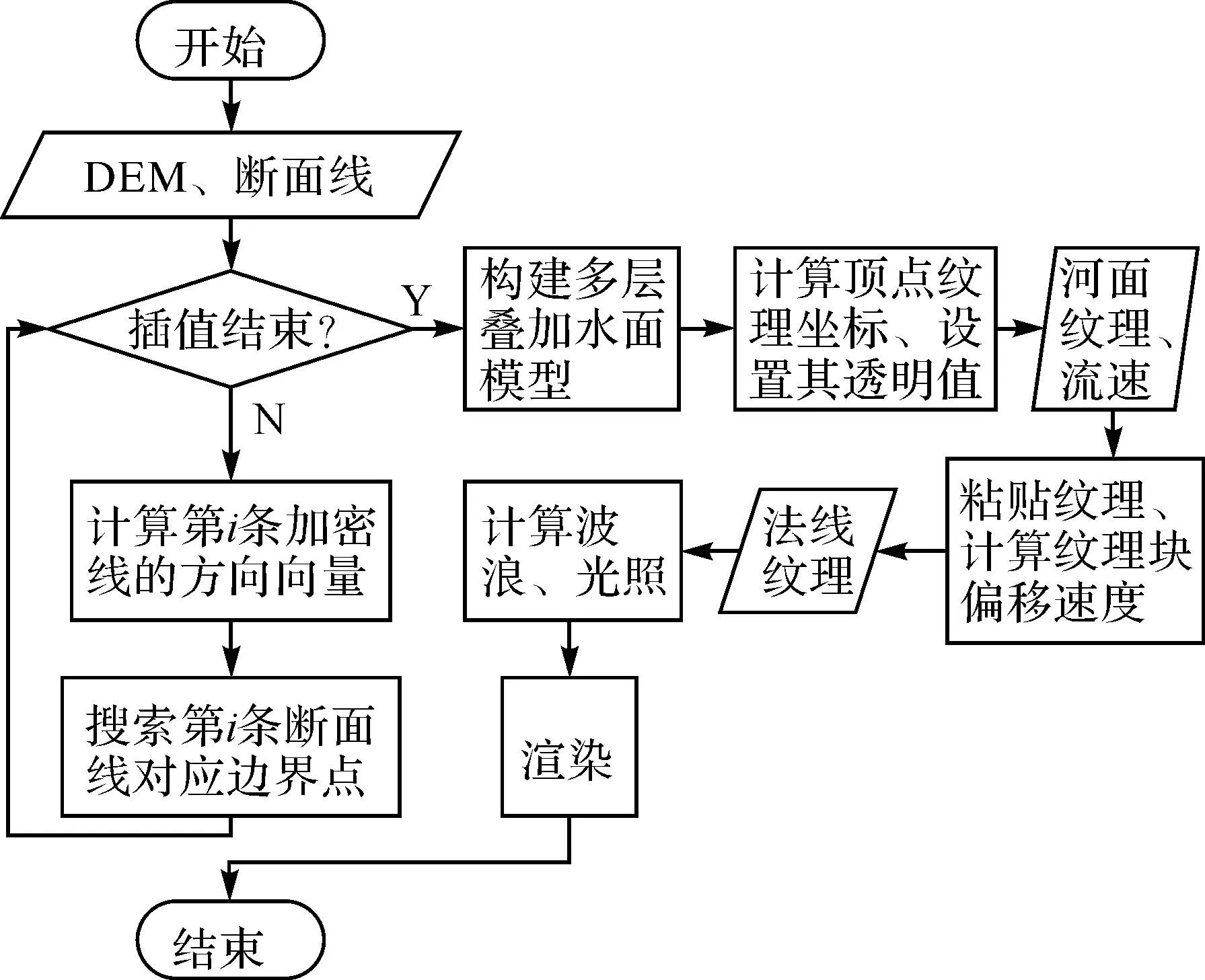
图1 流动水体仿真流程
1. 河流边界提取
如图2所示,(a)为初始断面水位线分布图,(b)为经过边界搜索算法处理后的断面水位线分布图,其中的虚线为加密插值的断面线。
(1) 边界点搜索算法
由于河面水位随时间变化,初始断面水位线两端点并不一定恰好处在实际水位河面边界线上,实测断面水位线与实际水位之间的分布关系如图3所示。
以左岸端点aL情形为例,数据处理的最终目标是要将aL点转换至与bL点重合或靠近的ab处。由于aL点高程ha比实际水位高程h高,其边界点搜索流程如下:

图2 河流边界线提取

图3 断面水位线

2) 在采样离散点的同时计算各点an+1(n≥0,a0即为aL点)的高程hn+1与水位高程h之差hΔ(hn+1-h)。
3) 若hΔ的绝对值小于或等于预先设定阈值ht,则认为采样点an+1位于河流边界线上,算法结束;若hΔ为负且绝对值大于ht,即点an+1位于远离边界线的水面以下,算法继续执行进入第4)步。
4) 采用二分法在an与an+1之间进行反复迭代插值,直至获取某点ab的高程与水位高程之差绝对值小于ht,即得到水面边界点ab。
采用该算法对所有断面水位线进行处理,完成边界点的提取。
(2) 断面水位线加密
整条河流按水位线分成若干小段,分别对各小段河流依次进行加密插值。为了达到如图2(b)所示的插值效果(断面线的分布在河流弯道的外侧比内侧稀疏,这样才能更好地表达水面各处流速情况),以第k(上游)和k+1(下游)断面之间河段为例,插值加密由第k个断面开始沿着河道向第k+1个断面逐渐靠近依次进行,边界线搜索具体步骤如下:
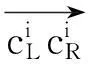

(1)
式中,向量均为同一坐标系下的单位向量;Qk表示第k个初始断面的起点距(以河流上游或是下游某断面中心点为参照沿河流中心线计算的各断面距参照点的路程);d1为断面插值采用的步长,具体值视仿真需求决定(如取10m)。
3) 对ki断面水位线,依次进行下列过程:
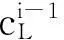
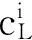
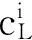

e. 依据断面k和k+1的水位高程值,利用线性插值计算得到断面线ki的水位高程值。
由于河流的自然走势,自上游至下游会出现高程起伏变化,沿着河道不同处的断面水位线处于不同的水平面,另外各个河流分段内水位的变化很小,可以看成是由上游至下游呈线性降低,因此算法中采用线性插值得到加密断面线的水位高程。
2. 流动水体仿真
(1) 水面建模
本文在水面模型的建立上改为在传统的单层格网模型之上再叠加两层横纵向的带状三角锁网,如图4所示。
首先利用前文方法处理得到的河流边界及插值加密断面水位线数据,在每一条断面水位线上加密采样一系列点,建立第1层基本河面三角网,如图4(a)所示。
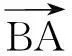

图4 3层河面网格模型
(2) 纹理映射技术
① 纹理坐标求解
在计算第1层基本河面网格的纹理坐标时,按照横向纹理贴图的重复次数线性计算出各个模型顶点的纹理U坐标,即河流断面线上各个顶点的U坐标间距相等,在河面宽处纹理会被拉伸,河面狭窄时纹理会被压缩。而V方向即沿着河流流动方向的纹理坐标计算,首先设整段河流纹理纵向贴图重复次数为Tv,第一个断面起点距为0,最后一个断面起点距为Qend(单位为m),则各个顶点的V方向纹理坐标计算如下
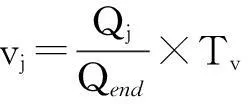
(2)
式中,Qj为第j个断面的起点距。在计算第2层和第3层网格顶点的纹理坐标时,只需根据相应r和t(含义如上文)的取值,以第1层网格纹理坐标为基准进行插值计算即可,如第1层中A点纹理U坐标为uA,B、D纹理V坐标为vB和vD,则第2层中的p1点和第3层中的q2点的纹理坐标up、vq则分别如下

(3)
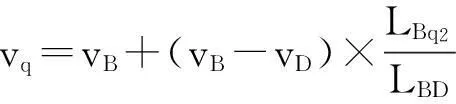
(4)
式中,T为横向(沿河流断面线方向)纹理重复贴图次数;N为断面线上顶点数,每个断面线上顶点数均为N;LAp1、LAE、LBq2、LBD分别为线段Ap1、AE、Bq2、BD的长度,单位为m。
② 动态纹理映射
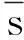

(5)
式中, f为渲染的实时帧率。但该值为不可预知的随机值,实际应用中无法利用其计算纹理偏移值,在本文的渲染中计算vm时f不参与计算,即整体纹理偏移速度统一放大f倍,但这不会影响最终渲染视觉效果,如果需要获取实时水流速度,只需利用测量值除以实时帧率即可。其他参数与前文含义相同。由于各个纹理块的vm不等,因此能表现河面各处流速不同。
③ 纹理融合
随着时间推移,由于第1层河面网中各个独立四边形块之间纹理偏移不同步(由于vm不等)导致纹理被拉扯错位,每一四边形块各自流动犹如水面被切开一样,使得河面看起来如马赛克一般支离破碎。为了克服这一缺陷,让各个四边形纹理块之间自然平滑过渡,相互交融成为一个自然的整体河流,依据之前计算的顶点纹理坐标,在第2层和第3层融合带模型上粘贴纹理。然后设定融合带各纹理块偏移的速率。如图4中,第2层的纵向纹理在进行纹理渲染时,设定纹理块FAp1p2的偏移与FGBA的纹理偏移同步,第3层的横向纹理块如图4中设定ABq2q1与ABCD的纹理偏移同步,即横、纵向融合纹理带中各个纹理块的偏移与其临边的第一层纹理块偏移同步。最后针对融合带每一纹理块进行透明渐变的设定,如纹理块FAp1p2中,设定A、F点透明度值(Alpha值)为1(即不透明),而p1、p2点设为0,由此在纹理渲染过程中实现了从AF线到p1p2线的逐渐透明的效果,从而使得纹理块FGBA自然地与EIFA模糊融合为一张更大的纹理块。同样设置A、B点透明度值为1,设定q1、q2点为0,实现ABCD与FGBA的自然融合。整个河面网中都对相应顶点进行透明值的设置,从而实现了整条河流的纹理块融合,效果如图5所示。
④ 纹理渲染

图5 流动水体仿真效果
考虑到水文工作更多的实用性需求及系统效率,本文使用水面波纹法线贴图(如图6(b)所示)利用法线映射技术实现了简单的水面波动及光学效果,采用HLSL语言编写着色器结合最终完成纹理的渲染。河流水体的颜色由下式决定
Cwater=α×Cpicture+β×Cambient+γ×Cdiffuse+
λ×Cspecular+θ×Creflect
(6)
式中,Cwater为水面颜色;Cpicture为河面图像颜色;Cambient为环境光颜色;Cdiffuse为漫反射颜色;Cspecular为镜面高光颜色;Creflect为反射颜色。各项值的具体计算目前已有成熟公式,此处不再赘述。对于系数α、β、γ、λ、θ满足和值为1,且取值都分别位于[0,1]之间,具体取值视仿真效果而定。

图6 本文所使用的纹理
三、试验与分析
1. 数 据
根据本文提出的方法,笔者在Windows7系统上以GaeaExplorer2.0为平台结合VisualStudio2008及DirectX9.0环境,采用C#和HLSL语言,在长江流域三峡大坝上游段的区域内构建了流域动态水体仿真系统作为试验环境,在该仿真系统中可以自由漫游浏览水体流动效果。试验中DEM数据为30m精度的SRTM地形数据和5m精度的河道地形数据,同时影像数据为30m精度的Landsat影像数据。试验区域内整个河流长度为605km,初始断面水位线共308条,所有水文观测数据均存储在数据库中。试验硬件环境为:Intel(R)Core(TM)2DuoCPU,2.0GB内存,2.66GHz,ATIRadeonHD3450显卡,显存256MB。
2. 试验结果与分析
图5(a)中红色曲线为利用本文算法搜索出来的河流边界线,可见河流边界线与自然河道地形能较好地贴合。图5(b)、(c)为未进行动态纹理渲染前静止河流水面的模拟效果,实现了简单的波纹、反射、高光等水面现象,图5(d)、(e)、(f)是粘贴了河面图像纹理,采用本文提出的动态纹理渲染技术表达的流动河流水面效果,在系统中能动态观察到水面各处的流速不同的自然现象。
不同河流长度建模与渲染效率见表1。
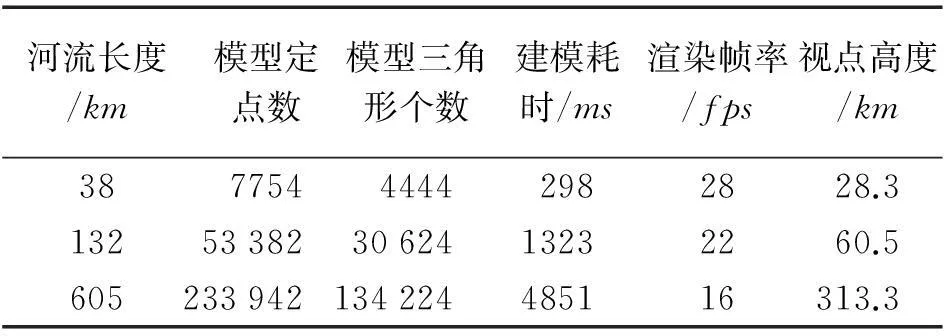
表1 建模与渲染效率
表1中视点高度值表示在仿真窗口中(视域内)能够看到整段河流时相机离地面的最低高度。本文采取对所选河段进行一次性统一建模。河流长度为605km时,渲染帧率达到16帧,建网耗时4851ms,能够实现整个仿真系统的连贯流畅运行,仿真效率较好。但此时在313.3km高度看到的河流近乎为一条细线,无法观察河面细节情况,而当相机靠近河面观察时又只有整条河流的一小段进入视域内,因为本文试验中采取对整条河流一次性统一建模,其余部分虽然不在视域内但同时也在进行渲染,这就在无形之中大大降低了系统运行效率。为了进一步提高效率,可以考虑随时只对视域内的河流段进行仿真,从而保证效率,满足实际工作需求。在本试验系统中相机高度在低于7652m时才能清楚观察河面水流流动情况,此高度下出现在视域内河流长度在12km左右。可以将河流分为12km左右的小段,在仿真时动态地对进入视域内的河流段利用本文仿真方法进行建模与渲染。
四、结束语
本文提出的方法不仅能利用断面水位线结合DEM进行河流边界自动搜索及河面自动建模,也具有较好的仿真效果,能够真实表达出整个河面各处流速情况,尤其是水面多层模型的建立对于表达流动水体自然特性的模拟具有较好的借鉴意义。因为断面线及DEM在水文工作中属于基本数据,容易获得,所以本文方法具有较好的普遍适用性。但是在支流处,本文的边界搜索算法无法智能实现断面处理,需要人工干预河流断面线的加密,针对这种情况还需作进一步研究。
参考文献:
[1]陈文辉,谈晓军,董朝霞.大范围流域内水体三维仿真研究[J].系统仿真学报,2004,16(11):2409-2412.
[2]王伟,王鹏,陈能成,等.一种面向大区域不规则河道的水流仿真方法[J].武汉大学学报:信息科学版,2011,36(5):510-513.
[3]童俊涛.面向大区域不规则河道的河水建模与渲染的研究[D].武汉:武汉大学,2010.
[4]王玮哲. 面向大范围地理环境的河流建模与渲染方法研究[D]. 武汉:武汉大学,2011.
[5]冯玉芬.基于虚拟现实技术的动态水面仿真方法研究[J].唐山师范学院学报,2012,34(2):52-55.
[6]王海玲,印桂生,张菁,等.基于改进曲面熵的动态水面模拟方法[J].计算机工程,2011,37(6):24-26.
[7]王道臣,万旺根,唐经洲,等.基于GPU的水面实时渲染算法[J].计算机工程,2008,34(20):233-234.
[8]方贵盛,潘志庚.水虚拟仿真技术研究进展[J].系统仿真学报,2013,25(9):1981-1989.
[9]杨在兴,芮小平,梁明,等.基于流场的流动水体仿真[J].计算机工程与设计,2012,33(6):2392-2396.
[10]冶运涛,张尚弘,王兴奎.三峡库区洪水演进三维可视化仿真研究[J].系统仿真学报,2009,21(14):4379-4382.
[11]孟令奎. 吕琪菲复杂水体边界提取的改进正交T-Snake模型[J].测绘学报,2015, 44 (6): 670-677.
[12]朱长明, 骆剑承, 沈占锋, 等.DEM辅助下的河道细小线性水体自适应迭代提取[J]. 测绘学报,2013, 42 (2): 277-283.

