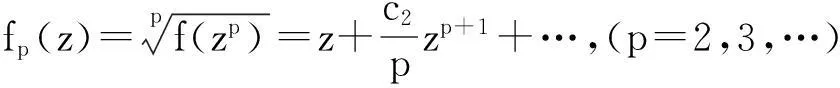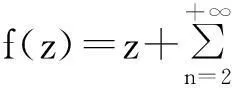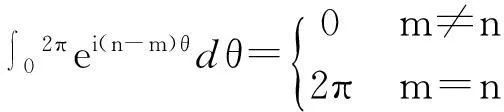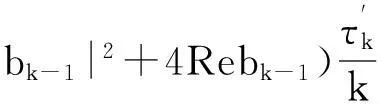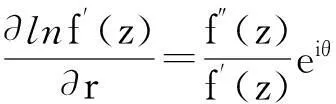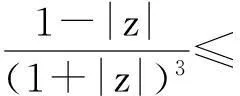一类单位圆上单叶正则函数的分类

李小光

(西安航空学院理学院， 陕西 西安 710077)



一类单位圆上单叶正则函数的分类

李小光

(西安航空学院理学院， 陕西 西安 710077)

摘要：为研究单位圆上单叶正则函数的性质。运用单叶解析法得到零点处函数值等于零、导数值等于1的函数具有的一些重要性质，给出这些性质的分类，分别是：幂级数展式的系数估计、模的估计、像区域范围的估计。单叶正则函数的性质及其分类是研究复变函数几何理论的基础，对复变函数基础性研究具有一定的现实意义。

关键词：单叶解析; 系数估计; 模的估计; 像区域范围的估计

定义1 令n=1,2,…，对于k=1,2,…,n，称

τk(t)=

(1)

为deBranges函数[1]。其中(a)v是a(a+1)…(a+v-1)的缩写。

如果令τk+1(t)≡0，则有

(2)

还可以得到[1]

τk(0)=n+1-k

(3)

τ′(t)<0, 0

(4)

(5)

1系数的估计

|cn|≤n, (n=1,2,…)

(6)

|c2|≤2

(7)

(8)

证明设圆周|z|=ρ<1由w=f(z)=

(n=1,2，…)

(9)

f(z,t)=etz+…(z∈D), 0≤t<+∞

(10)

使f(z,0)=f(z)，且

(11)

其中χ(t)在0≤t+∞连续，且|χ(t)|=1。

适合f(D)/J的函数f在S中就D内局部一致收敛来说是稠密的，因此仅需对这些函数证明式(9)。

(12)

(13)

记b0(t)=0，

(14)

由式(14)得

(15)

令n=1,2,…固定,考虑

t<+∞)

(16)

其中τk(t)是deBranges函数。

2模的估计[6-8]

记z=reiθ，则上述不等式可写为

(17)

又因为lnf′(z)=[|lnf′(z)|+iargf′(z)][3]

即

(18)

(19)

由式(17)-(18)，可得到下列定理

定理6(变形定理)设f(z)在|(z)|<1上单叶解析,f(0)=0，f′(0)=1,则

(20)

(21)

(22)

同理在式(18)两边从0到r积分得

(23)

沿着直线从0到z对式(11)的右边积分

考虑圆周|z|=r上的像点w，将w=0与w以直线段连接，这条直线段的原像是L，则

综合以上积分得到

(24)

3像区域范围的估计

定理7 (面积掩蔽定理)[10]设函数f(z)=

证明如果点c不在w=f(z)的像区域B内，则函数

推论1[11]如果f(z)在|z|<1上单叶解析，f(0)=0，在圆|z|<1上不取数值c，则f′(0)≤4c。

参考文献：

[1]Imai Y, Iseki K.On axiom systems of propositional calculi xiv[J].Proc.Japan A cademy,1966,(42):19-22.

[2]Borzooei R A,HasanKhani A,Zahedi M M.On hyper k-algebras[J].Mathematicae Japonicae,2000,52(1):113-121.

[3]Borzooei R A ,Harizavi H .Regular Congruence relations on hyper Bck-algebras[J].Scientiae Mathematicae Japonicae,2005,61(1):83-97.

[4]Bakhshi M, Borzooei R A. Lattice structures on fuzzy congruence relations of a hypergrouoid [J]. Information Science,2007,177(16):3305-3313.

[5]Borzooei R A,Zahedi M M.(Anti) fuzzy positive implicative hyper k-ideals[J].Italian J. Pure and Appl.Math,2003,(14):9-22.

[6]王国俊. 非经典数理逻辑与近似推理[M].北京:科学出版社,2000.

[7]吴忘名.Fuzzy蕴含代数[J].模糊系统与数学，1990,4(1)：56-63.

[8]谢云鹏. 基于包含度的模糊不定性度量[D].西北大学,2008:18-28.

[9]姚炳学.群和环上的模糊理论[M].北京:科学出版社,2007:84-88.

[10]戈鲁辛.复变函数的几何理论[M].北京：科学出版社,1956.

[11]钟玉泉.复变函数[M].北京：高等教育出版社,2003.

Classification of a Class of Univalent Regular Functions on the Unit Circle

LI Xiao-guang

(College of Science, Xi'an Aviation College, Xi'an, Shaanxi 710077,China)

Abstract:In this paper, the properties of univalent regular functions on the unit circle are studied. Through univalent analytical method, some important properties are introduced when some properties classification are given, these properties are the coefficients estimation of expansion of power series, the estimation of model and the estimation of the domain of image. Properties and classification of univalent regular function is the basis of geometric theory of function of complex variable, which has practical significance to the study of function of a complex variable.

Key words:univalent analysis; the coefficients estimation; the estimation of model; the estimation of the domain of image

中图分类号：O175.14

文献标识码：A

文章编号：1671-9131(2015)04-0012-04

作者简介：李小光(1973-)，女，辽宁铁岭人，副教授，从事代数学及信息论方面的研究。