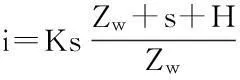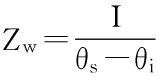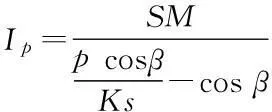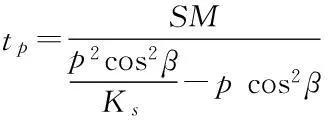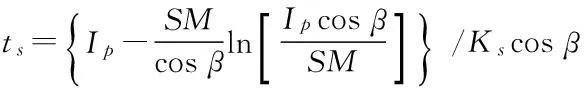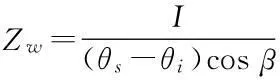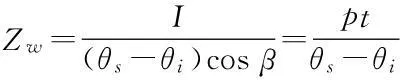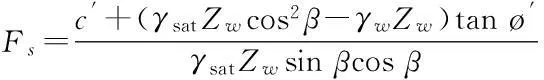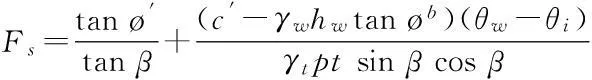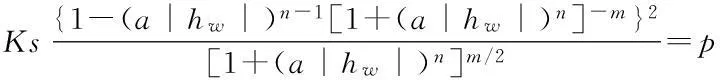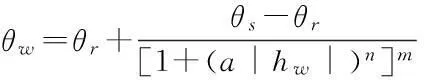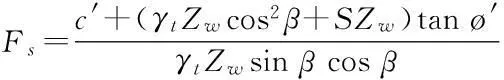基于Mein-Larson入渗模型的浅层降雨滑坡稳定性研究*

李秀珍，何思明

(1. 中国科学院山地灾害与地表过程重点实验室, 四川 成都 610041；2. 中国科学院·水利部　成都山地灾害与环境研究所, 四川 成都 610041)



基于Mein-Larson入渗模型的浅层降雨滑坡稳定性研究*

李秀珍1，2，何思明1，2

(1. 中国科学院山地灾害与地表过程重点实验室, 四川 成都 610041；2. 中国科学院·水利部成都山地灾害与环境研究所, 四川 成都 610041)

摘要:降雨入渗模型与边坡稳定性方法有机结合是研究降雨诱发滑坡稳定性的有效方法。在深入分析降雨入渗基本理论的基础上，将Mein-Larson入渗模型与基于饱和土、非饱和土以及近似非饱和土的无限边坡稳定性分析方法有机结合，综合考虑了高强度短历时和低强度长历时两种降雨情形，拓展并改进了基于Green-Ampt入渗模型的饱和土和近似非饱和土无限边坡稳定性模型，并依托典型边坡实例对各评价模型的计算结果和适用性等进行了对比分析。

关键词:Green-Ampt；Mein-Larson；入渗模型；降雨；滑坡；稳定性；无限边坡

降雨滑坡在世界上不仅分布广泛，发生频率高，而且给人类造成的危害也极为严重。国内外大量相关资料表明[1-3]，60%～80%的滑坡发生于雨季(如1989年7月四川华蓥市溪口滑坡、2004年9月四川宣汉天台乡滑坡、2010年贵州关岭滑坡等)，而发生于冬春季节的许多大型滑坡往往也与降水或融雪入渗的滞后效应有关(如2013年1月云南镇雄滑坡、2013年3月西藏墨竹工卡滑坡等)。

目前，降雨入渗模型与边坡稳定性方法有机结合是研究降雨型滑坡的有效方法[3]。1911年Green和Ampt提出了Green-Ampt干土积水入渗模型。该模型因其形式简单，物理概念明确且具有良好的扩展性，已成为描述垂直入渗过程中应用最为广泛的入渗模型之一[4]。1973年Mein和Larson将Green-Ampt模型应用于降雨入渗的场合，建立了Mein-Larson降雨入渗模型[5-8]。在降雨诱发浅层滑坡的稳定性评价中，陈晓东等利用Mein-Larson入渗模型结合极限平衡方法，建立了一个降雨滑坡稳定性分析的通用模型[9]；Muntohar和Liao利用改进的Green-Ampt模型结合无限边坡稳定性分析方法，并考虑了土体的非饱和特性，提出了一个基于修正Green-Ampt模型的近似非饱和土无限边坡稳定性分析模型[10]；Xie等将Green-Ampt模型与饱和土无限边坡稳定性分析方法相结合，并考虑了滑面与湿润锋面、地下水位面以及基岩面等的相关关系，提出了一系列降雨诱发浅层滑坡稳定性的计算模型[11]；李宁等采用常用的非饱和土VG模型与改进的Green-Ampt模型对Mein-Larson降雨入渗模型进行改进，将改进后的降雨入渗模型与非饱和土无限边坡稳定性分析方法相结合，提出降雨入渗诱发浅层滑坡的简化计算模型[3]。这些模型均为Green-Ampt和Mein-Larson入渗模型在浅层降雨滑坡稳定性评价中的广泛应用提供了良好的理论基础。但是除李宁模型外，其他模型中的入渗模型均未全面考虑高强度短历时和低强度长历时两种降雨情形。

鉴于此，本文将在分析降雨入渗基本理论的基础上，综合考虑高强度短历时和低强度长历时两种降雨情形，将Mein-Larson入渗模型与基于饱和土、非饱和土以及近似非饱和土的无限边坡稳定性分析方法有机结合起来，评价降雨诱发浅层滑坡的稳定性，并依托典型边坡实例对各模型的计算结果和适用性等进行了分析对比。

1基于Mein-Larson入渗模型的浅层降雨滑坡稳定性分析

1.1降雨入渗基本理论

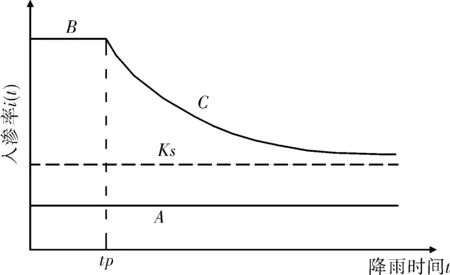
已有研究成果表明[5，12-14]，在恒定降雨条件下，降雨入渗过程的变化主要取决于降雨强度p和土体饱和渗透系数Ks。根据p/Ks的大小，可以将降雨入渗过程大致划分为以下两种情况[5]。

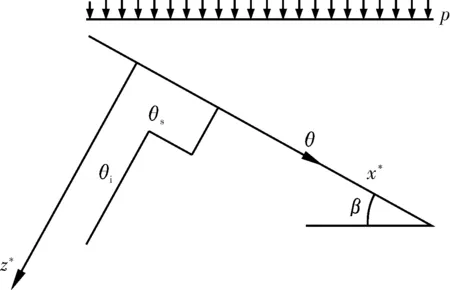
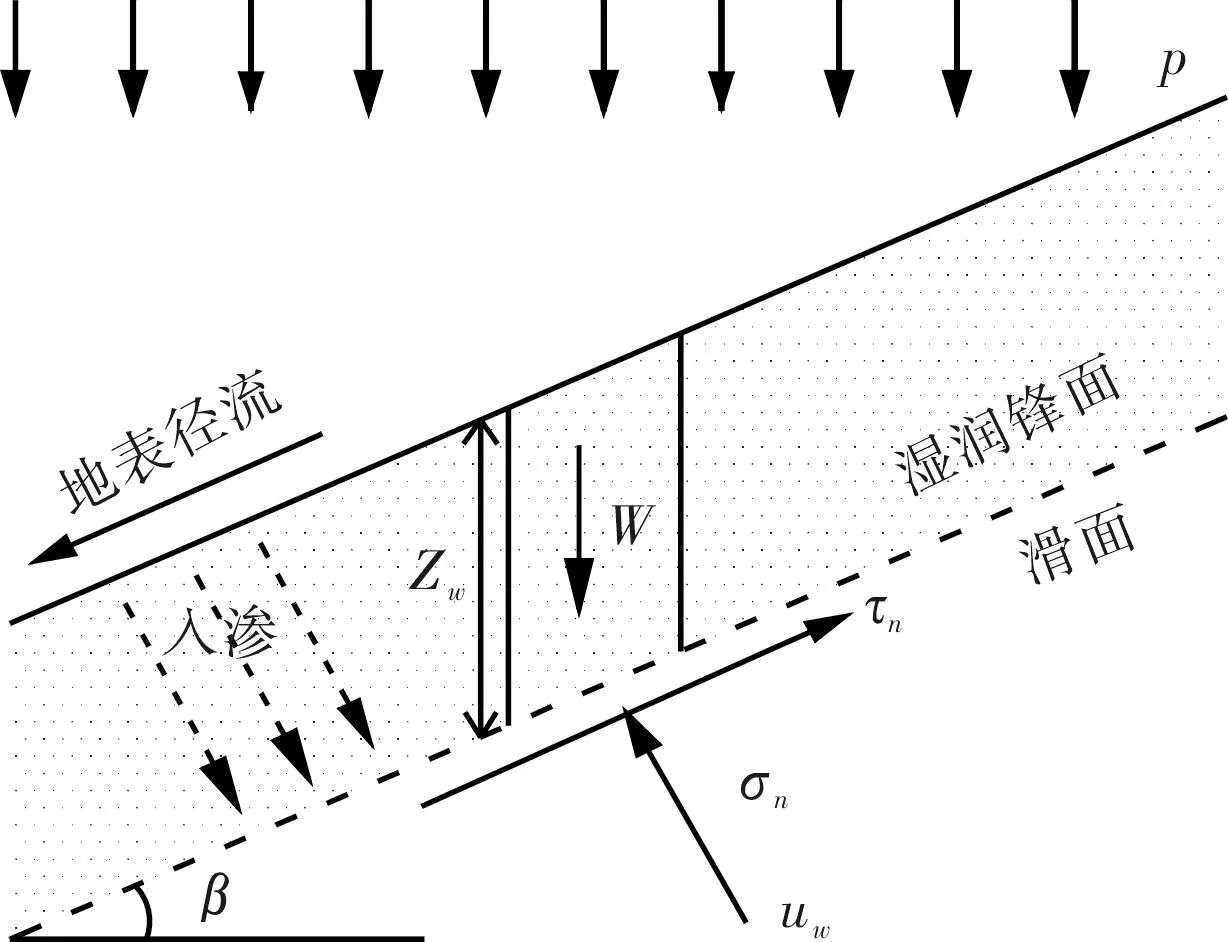
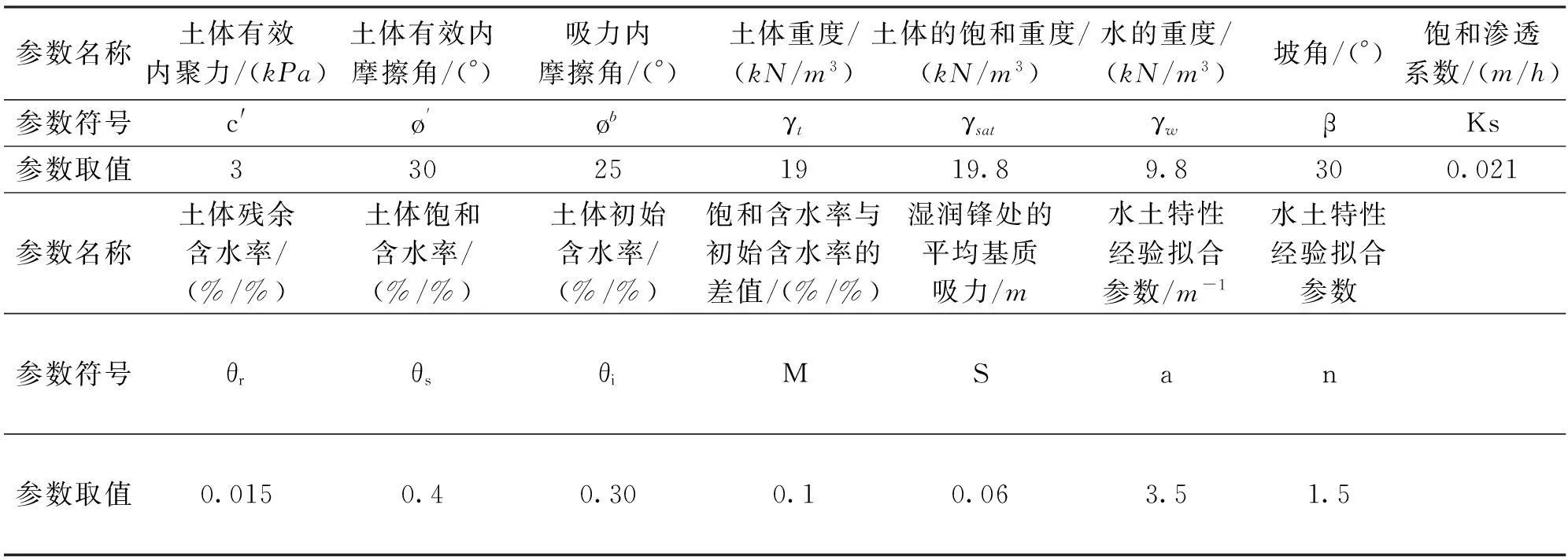
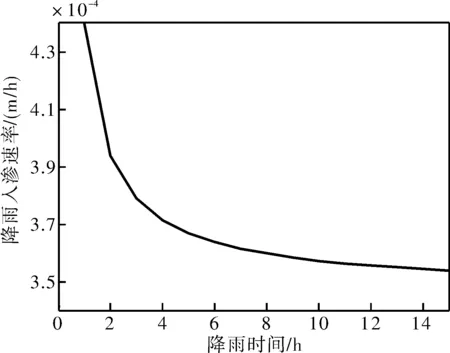
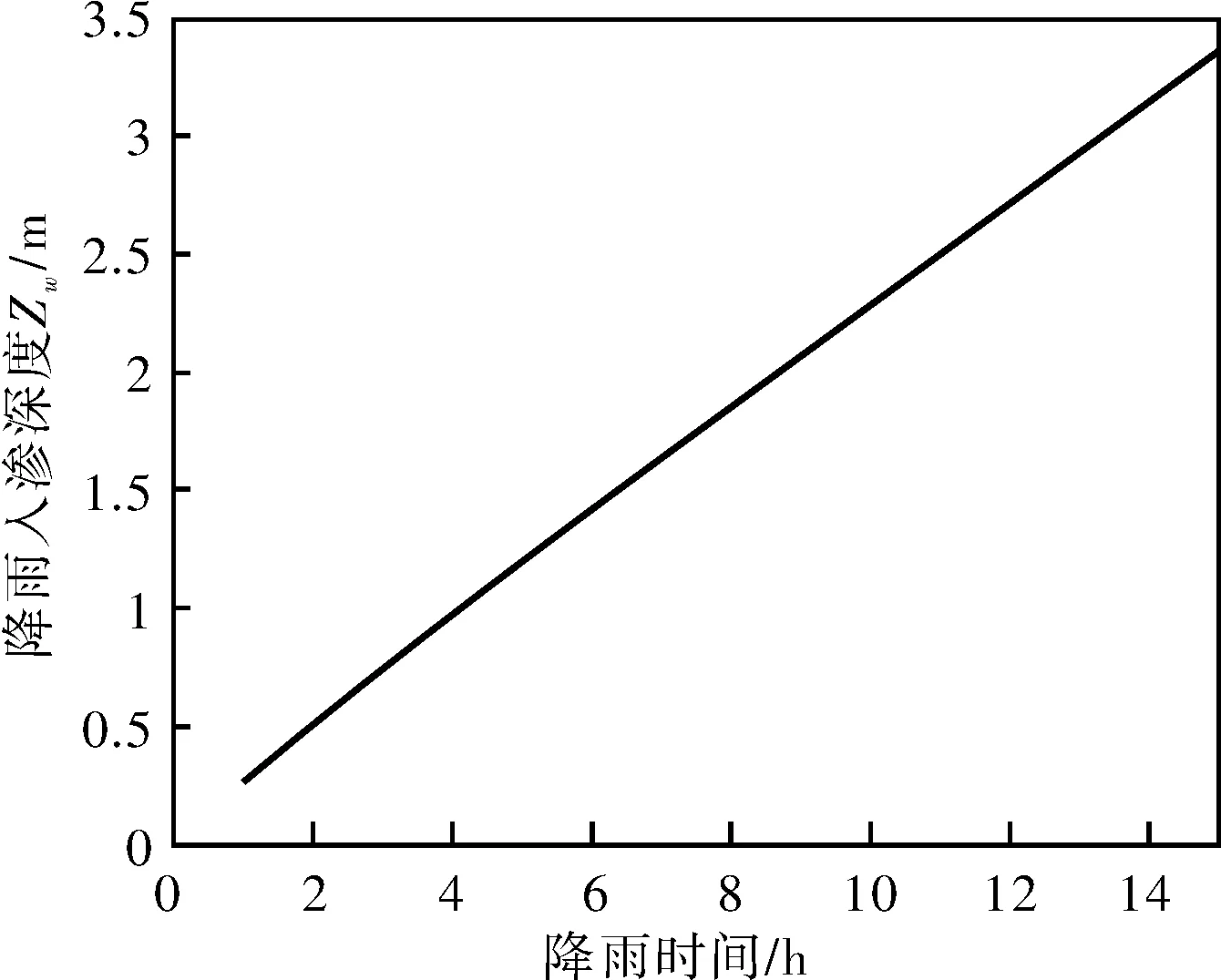
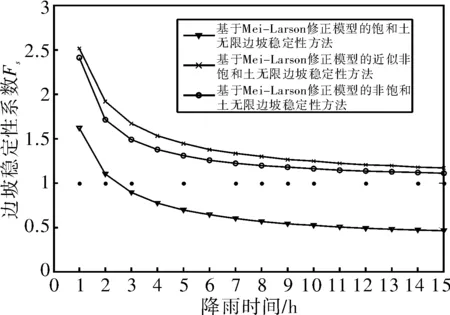
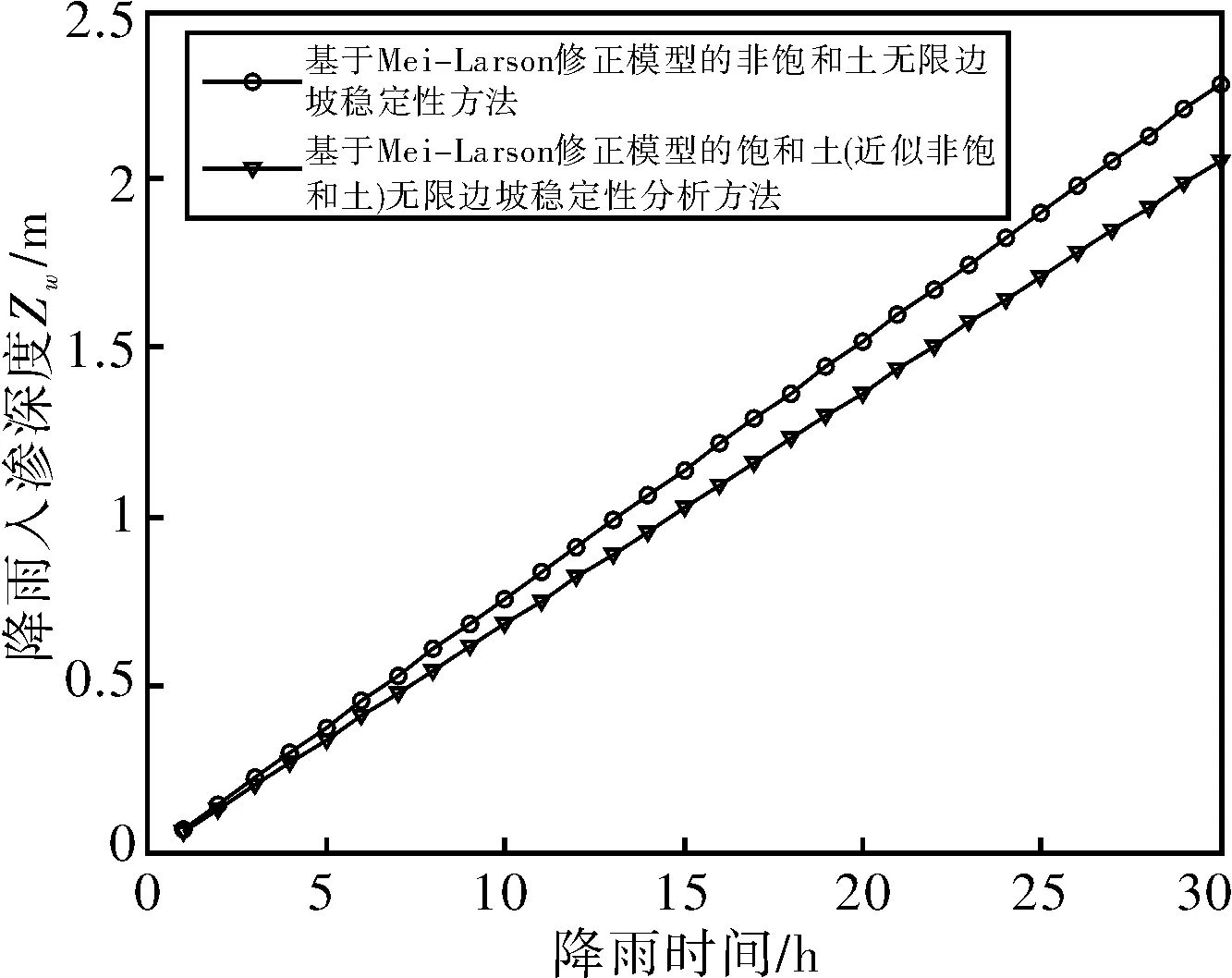
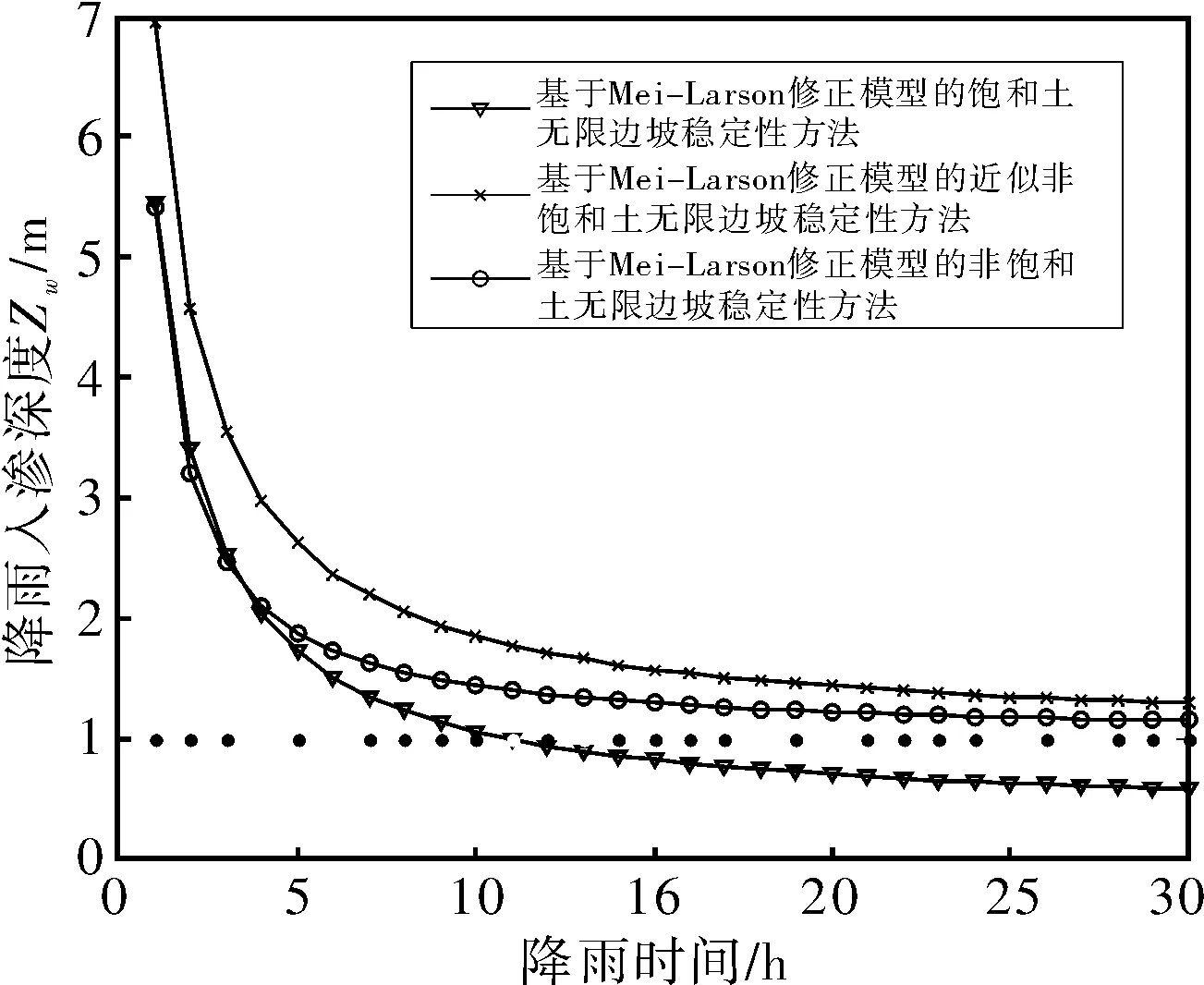
(1)无积水入渗：当p

(2)有积水入渗：当p>Ks时，在降雨初期，由于土体吸水率很大，降雨全部渗入土体中，但随着降雨的继续入渗，在降雨的中后期表层土体达到饱和，土体压力水头为零时，地表产生积水(图1中BC线段中的B段)。随着降雨强度持续地超过土体饱和渗透系数，降雨积水入渗从积水点开始继续，并随着降雨时间的延续而衰减(图1中BC线段中的C段)。

图1　恒定降雨条件下降雨入渗过程示意图

1.2Green-Ampt入渗模型

Green和Ampt早在1911年就根据毛管理论提出了近似积水模型。该模型是研究初始干燥的土壤在薄层积水时的一维平面入渗问题。由于Green-Ampt模型形式简单，且物理概念清晰，已成为描述垂直入渗过程中应用最为广泛的入渗模型之一。其基本假定是：①渗入土壤中的水分从土壤表面至入渗锋面沿深度的水分分布是均匀的，同时是饱和的；②入渗时存在着明确的水平湿润锋面，将湿润的和未湿润的区域截然分开，湿润区土壤含水量为饱和含水量，未湿润区则为初始含水量。

根据达西定律，可求出地表处的入渗率为：

(1)

式中：Ks为土体饱和渗透系数(饱和导水率)(m/h)；s为湿润锋平均基质吸力(m)；Zw为概化湿润锋深度(m)；H为地表积水厚度(m)；i为降雨入渗率(m/h)。

由水量平衡原理，可求得累积入渗量I与湿润锋深度Zw的关系为:

(2)

式中：I为累积入渗量；θs为饱和含水率；θi为初始含水率。

1.3Mein-Larson降雨入渗模型

Mein-Larson模型是Mein和Larson于1973年将Green-Ampt模型应用于降雨入渗条件下提出的。该模型假定在降雨入渗过程中湿润锋平行向下推进，传导区含水率均匀分布。最初的Mein-Larson模型只考虑了坡面有积水的情形，而且坡面为水平面。根据降雨入渗的基本理论，下面主要分两种情形对恒定降雨条件下经过坡度修正后的Mein-Larson模型进行简要介绍。降雨入渗模型计算简图如图2所示。

图2　降雨入渗模型计算简图

图2中，x*、z*分别为平行与垂直坡面的坐标方向；θs为边坡土体的饱和含水率；θi为边坡的初始体积含水率；β为边坡坡角。

(1)降雨强度p大于土体饱和渗透系数Ks

设稳定的降雨强度为p，当p大于土体的入渗能力时，地表才形成积水。假设当累计入渗量达到某一Ip值时，入渗率等于降雨强度(i=p)，此时开始积水，则可导出开始积水时的累计入渗量Ip：

(3)

式中：S为湿润锋平均基质吸力(m)，M为饱和含水率与初始含水率的差值(%/%)，即M=θs-θi。

积水时间tp为：

(4)

各时段的累积入渗量I为：

(5)

式中：ts为t=0开始积水，到累计入渗量I=Ip时所需要的时间，其计算公式为：

(6)

根据式(2)，可得出湿润锋的竖直入渗深度Zw为：

(7)

(2)降雨强度p小于土体饱和渗透系数Ks

当降雨强度小于土体的饱和渗透系数时，降雨全部渗入土体中。考虑坡度对降雨入渗的影响，则有累积入渗量I为：

I=ptcosβ。

(8)

相应地，可得出湿润锋的竖直入渗深度Zw为：

(9)

式(7)和(8)中的参数同上。

1.4基于Mein-Larson模型的浅层降雨滑坡稳定性计算方法

无限边方法是山区平面滑动型边坡常用的稳定性分析方法。当边坡潜在滑面的深度与边坡长度之比很小时(一般深长比小于0.1时)，就可以把该边坡当作一个无限边坡进行分析。将Mein-Larson入渗模型与无限边坡稳定性分析方法相结合，不但可以考虑坡面倾斜的影响，而且可以同时考虑两种不同的降雨形式(低强度长持续时间和高强度短持续时间)下浅层边坡的稳定性随降雨时间的变化情况。二者相结合的计算简图如图3所示。

图3　无限边坡稳定性模型计算示意图

图3中，σn、τn为分别滑面上总的法向应力和切向应力，uw为孔隙水压力，其他参数同上。

根据降雨入渗后湿润锋以上土体所处的状态不同(饱和状态或非饱和状态)，提出以下三个Mein-Larson入渗修正模型与无限边坡稳定性分析方法相结合的计算模型。

模型1：基于Mein-Larson修正模型的饱和土无限边坡稳定性分析方法。

该模型假定湿润锋以上土体处于饱和状态。Xie等提出的Green-Ampt模型结合饱和土无限边坡的稳定性分析方法，仅针对降雨强度小于土体饱和渗透系数的情况。本研究拓展和改进了Xie-Tetsuro-Cai提出的模型，将Mein-Larson降雨入渗修正模型和饱和土无限边坡稳定性分析方法有机结合，综合考虑了降雨强度大于土体饱和渗透系数和降雨强度小于土体饱和渗透系数两种情况。主要计算公式如下所示。

①降雨强度p大于土体饱和渗透系数Ks时，边坡的稳定性系数Fs为：

(10)

式中：c′为土体有效内聚力(kPa)；ø′为土体有效内摩擦角；γw为水的重度(kN/m3)；γsat为土体的饱和重度(KN/m3)；β为边坡的坡角(°)；Fs为边坡稳定性系数。

降雨入渗深度Zw的计算同式(7)。

②降雨强度p小于饱和渗透系数Ks时，边坡的稳定性系数计算公式同式(10)，降雨入渗深度Zw的计算同式(9)。

模型2：基于Mein-Larson修正模型的非饱和土无限边坡分析方法。

参考文献该模型假定湿润锋以上土体处于非饱和状态。[3]，采用非饱和土Van Genuchten(VG)模型与改进的Green-Ampt入渗模型对Mein-Larson降雨入渗模型进行改进，将Mein-Larson降雨入渗修正模型与无限边坡稳定性分析方法相结合，主要计算公式如下所示。

①降雨强度p大于土体饱和渗透系数Ks时，边坡的稳定性系数Fs为：

(11)

式中：γt是土体的重度(kN/m3)，降雨累积入渗量I可通过式(4)、(5)和(6)求得，其他参数含义同上。

降雨入渗深度Zw的计算同式(7)。

②降雨强度p小于饱和渗透系数Ks时，边坡的稳定性系数Fs为：

(12)

(13)

(14)

m=1-1/n。

(15)

式中：θw为降雨入渗情况下传导区土体的体积含水率(%/%)；hw为含水率θw对应的压力水头(m)；øb为吸力内摩擦角(°)；a和n均为水土特性经验拟合参数；其他参数含义同上。

降雨入渗深度 可通过式(9)计算。

模型3：基于Mein-Larson修正模型的近似非饱和土无限边坡稳定性分析方法。

Muntohar和Liao利用改进的Green-Ampt模型结合无限边坡稳定性方法，并考虑了土体的非饱和特性，提出了一个浅层降雨滑坡的稳定性分析模型[10]。本研究将Mein-Larson降雨入渗修正模型与无限边坡稳定性方法相结合，并参考文献[10]考虑了土体的非饱和特性，提出了近似非饱和土无限边坡的稳定性分析方法，具体计算公式如下所示。

①降雨强度p大于土体饱和渗透系数Ks时，边坡的稳定性系数Fs为：

(17)

式中参数的含义同上。

降雨入渗深度Zw的计算同式(7)。

②降雨强度p小于饱和渗透系数Ks时，边坡的稳定性系数计算公式同式(17)，降雨入渗深度Zw的计算同式(9)。

表1　边坡相关参数取值表

2浅层降雨滑坡稳定性计算方法的对比分析

以文献[3]中提出的边坡数据为例，对上述降雨诱发浅层滑坡的稳定性计算模型进行分析对比。边坡的几何、物理力学性质及水文等参数详见表1。

下面分高强度短历时和低强度长历时两种降雨条件进行分析。

(1)高强度短历时降雨(降雨强度大于土体饱和渗透系数的情形)假设降雨强度p=0.024 m/h，降雨时间为15 h。利用Mein-Larson修正模型计算求得的降雨入渗率和入渗深度随时间的变化情况分别见图4和图5。基于Mein-Larson修正模型的浅层降雨滑坡稳定性模型的计算结果见图6。

图4　降雨入渗速率随时间的变化曲线

图5　降雨入渗深度随时间的变化曲线

从图4和图5可以看出，当降雨强度大于土体饱和渗透系数时，降雨入渗速率随降雨时间的延续逐渐降低，最终趋于稳定，降雨入渗深度随降雨时间的延续呈线性关系增加。

从图6中可以看出，坡体在同等降雨条件下，当降雨强度大于土体饱和渗透系数时，近似非饱和土无限边坡模型的稳定性系数最大，其次是非饱和土无限边坡模型，稳定性系数最小的是饱和土无限边坡模型。而且，在不同降雨时刻，近似非饱和土模型与非饱和土模型计算的稳定性系数非常接近，二者的残差平方和仅为0.198 8。

图6　边坡稳定性系数随降雨时间的变化曲线

(2)低强度长历时降雨(降雨强度小于土体饱和渗透系数的情形)

假设降雨强度p=0.006 8 m/h，降雨时间为30 h。由于降雨强度小于土体饱和渗透系数，此时的降雨入渗速率等于0.006 8 m/h。利用降雨入渗模型计算求得的降雨深度随时间的变化情况见图7。基于Mein-Larson修正模型的浅层降雨滑坡稳定性模型的计算结果见图8。

从图7可以看出，在同等条件下，当降雨强度小于土体饱和渗透系数时，在不同降雨时刻，非饱和土无限边坡模型的降雨入渗深度总是大于饱和土和近似非饱和土无限边坡模型的降雨入渗深度。

从图8可以看出，当降雨强度小于土体饱和渗透系数时，三个模型中，近似非饱和土无限边坡模型的稳定性系数最大。在降雨初期，饱和土无限边坡模型的稳定性系数略大于非饱和土无限边坡模型的稳定性系数，当降雨时间达到一定时段后，非饱和土无限边坡模型的稳定性系数明显大于饱和土无限边坡模型的稳定性系数。

图7　降雨入渗深度随时间的变化曲线

图8　边坡稳定性系数随降雨时间的变化曲线

3结论

(1)与其他浅层降雨滑坡稳定性计算模型比较，基于Mein-Larson入渗模型的三种浅层降雨滑坡稳定性计算模型，既考虑了坡面倾斜的影响，又考虑了高强度短历时和低强度长历时两种降雨情形，而且公式简单，便于计算，具有更广阔的应用范围。

(2)当降雨强度大于土体饱和渗透系数时，近似非饱和土无限边坡模型的稳定性系数最大，其次是非饱和土无限边坡模型，稳定性系数最小的

是饱和土无限边坡模型。且在不同降雨时刻，近似非饱和土模型与非饱和土模型的稳定性系数非常接近，二者的残差平方和仅为0.198 8。因此，此种情形下，为简化计算，可以用近似非饱和土无限边坡模型代替非饱和土无限边坡模型。

(3)当降雨强度小于土体饱和渗透系数时，近似非饱和土无限边坡模型的稳定性系数最大。在降雨初期，饱和土无限边坡模型的稳定性系数略大于非饱和土无限边坡模型的稳定性系数，当降雨时间达到一定时段后，非饱和土无限边坡模型的稳定性系数明显大于饱和土无限边坡模型的稳定性系数。

[1]Polemio M, Petrucci O. Rainfall as a landslide triggering factor: An overview of recent international research[J]. Landslides, 2000(3): 1219-1226.

[2]戚国庆. 降雨诱发滑坡机理及其评价方法研究[D]. 成都：成都理工大学，2004.

[3]李宁，许建聪，钦亚洲. 降雨诱发浅层滑坡稳定性的计算模型研究[J]. 岩土力学，2012，23(5)：1485-1490.

[4]陈力，刘青泉，李家春. 坡面降雨入渗产流规律的数值模拟研究[J]. 泥沙研究，2001(4)：61-67.

[5]Mein R G, Larson C L. Modeling infiltration during a steady rain[J]. Water Resources Research, 1973, 9(2): 384-394.

[6]Chen L, Young M H. Green-Ampt infiltration model for sloping surfaces[J]. Water resources research, 2006, 42(7):1-9.

[7]Chu S T. Generalized Mein-Larson infiltration model[J]. Journal of irrigation and drainage engineering, 1987, 113(2): 155-162.

[8]Chu S T. Infiltration during an unsteady rain[J]. Water Resources Research, 1978, 14(3): 61-466.

[9]Chen Xiaodong, Guo Hongxian, Song Erxiang. Analysis method for slope stability under rainfall action[J]. Landslides and Engineered Slopes, 2008(7): 1507-1515.

[10]Muntohar A S, Liao H J. Rainfall infiltration: Infinite slope model for landslides triggering by rainstorm[J]. Natural hazards, 2010, 54(3): 967-984.

[11]Xie M, Esaki T, Cai M. A time-space based approach for mapping rainfall-induced shallow landslide hazard[J]. Environmental Geology, 2004, 46(6/7): 840-850.

[12]王建新. 降雨非饱和入渗过程的水势描述及理论模型研究与应用[D]. 北京：清华大学，2010.

[13]何玉琼. 植被发育斜坡的稳定性研究[D]. 昆明：昆明理工大学，2009.

[14]余新晓，陈丽华. 人工降雨条件下的入渗实验研究[J]. 水土保持学报，1989，3(4)：15-22.

杨光，舒立福，孙思琦，等. 我国森林火灾中人员伤亡时空分布特征研究[J].灾害学, 2015,30(2):21-25. [YangGuang，ShuLifu，SunSiqi，etal.Temporal-spatialdistributionregularitiesofforestfirecasualtiesinChina[J].JournalofCatastrophology, 2015,30(2)：21-25.]

AStudyonStabilityofShallowRainfall-inducedLandslideBasedonMein-LarsonInfiltrationModel

LiXiuzhen1, 2andHeSiming1, 2

(1. Key Laboratory of Mountain Hazards and Surface Processes, Chinese Academy of Sciences, Chengdu 610041, China;

2. Institute of Mountain Hazards and Environment, Chinese Academy of Sciences, Chengdu 610041, China)

Abstract:The combination of rainfall infiltration models and slope stability methods is an effective way to study types of landslides. Based on thorough analysis on the basic theory of rainfall infiltration, Mein-Larson modified model is combined with infinite slope stability models of saturated soil, unsaturated soil and approximate unsaturated soil. According to two rainfall cases of short duration rainfall with high intensity and long duration rainfall with low intensity, the infinite slope stability model of saturated soil and approximate unsaturated soil based on Green-Ampt infiltration mode is extended and modified. Finally, the calculation results and applications of the models are analyzed and compared by a typical slope case.

Key words:Green-Ampt; Mein-Larson; infiltration model; rainfall; landslide; stability; infinite slope

doi:10.3969/j.issn.1000-811X.2015.02.004

中图分类号：P642.22; X43

文献标志码：A

文章编号：1000-811X(2015)02-0016-05

作者简介：李秀珍(1975-)，女，内蒙古卓资县人，博士，副研究员，研究方向为地质灾害评价及预测. E-mail：lxzljt@sina.com@sina.com

基金项目：中科院重点部署项目子课题(KZZD-EW-05-01-02)；中国科学院山地灾害与地表过程重点实验室自主组织基金项目(Y3K2040040)；国家重点基础研究发展计划(2013CB733205)

收稿日期：*2014-09-19修回日期：2014-11-18