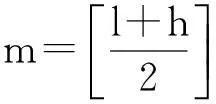一种无需借助栈的严格平衡二叉树建立

魏志威，王防修

(武汉轻工大学 数学与计算机学院，湖北 武汉 430023)



一种无需借助栈的严格平衡二叉树建立

魏志威，王防修

(武汉轻工大学 数学与计算机学院，湖北 武汉 430023)

摘要：针对当前严格平衡二叉树的建立需要借助栈来实现的问题，提出一种无需借助栈也能建立严格平衡二叉树的算法。为能对关键字进行二分查找，需要对现有的关键字序列进行排序,以便统计关键字的有序序列中每个关键字在二分查找时的比较次数。在统计完所有关键字的二分查找的比较次数后,通过关键字比较次数序列的排序得到严格平衡二叉树序列。最后，用非递归的二叉排序树插入算法依次插入严格平衡二叉树序列的每个关键字，得到的二叉排序树就是一棵严格平衡二叉树。算例仿真表明，无需借助栈也可建立一棵严格平衡二叉树。

关键词：选择排序；二叉排序树；严格平衡二叉树；二分查找；查找效率

1引言

在信息的查询中，二分查找由于具有较高的查找效率而受到人们的青睐。然而，二分查找[1]要求索引表在计算机内存里必须以有序顺序表的形式存放。如果内存中地址连续的空闲存储空间不够，则这样的顺序表无法建立，从而也就无法实现二分查找。与二分查找具有相同查找效率的是严格平衡二叉树，而严格平衡二叉树能充分利用地址不连续的空闲内存空间。因此，从内存管理[2]的角度出发，严格平衡二叉树的查询使用得更加广泛。

目前，建立严格平衡二叉树的方法不外乎两种，分别是递归算法[3-4]和非递归算法[5]。然而，无论是递归方法还是非递归方法，都需要借助栈。比如递归算法需要使用系统栈，而非递归算法则需要使用用户自定义栈。那么能否不使用栈也可建立严格平衡二叉树呢，本文将研究并解决该问题。

2建立严格平衡二叉树的原理

由输入的关键字序列建立的二叉排序树不一定是严格平衡二叉树，只有特定的关键字序列输入才能使得建立的二叉排序树是严格平衡二叉树。比如相同的整数关键字集合{6,7,8,9,10,11}，如果输入序列为8,7,6,11,10,9，则建立的二叉排序树不是严格平衡二叉树。相反，如果输入序列为9,7,6,8,11,10，则建立的二叉排序树就是严格平衡二叉树。由于二叉排序树可以在无需借助栈的情况下非递归建立，因此只要找到关键字集合的特定输入序列，则可以使建立的二叉排序树就是严格平衡二叉树。为叙述方便，不妨将这种序列称为严格平衡二叉树序列。

设X=x1x2…xn是由n个关键字xi(i=1,2,…,n)组成的关键字序列，如果能将其转化为一个严格平衡二叉树序列Y=y1y2…yn，则由Y建立的二叉排序树就是严格平衡二叉树。

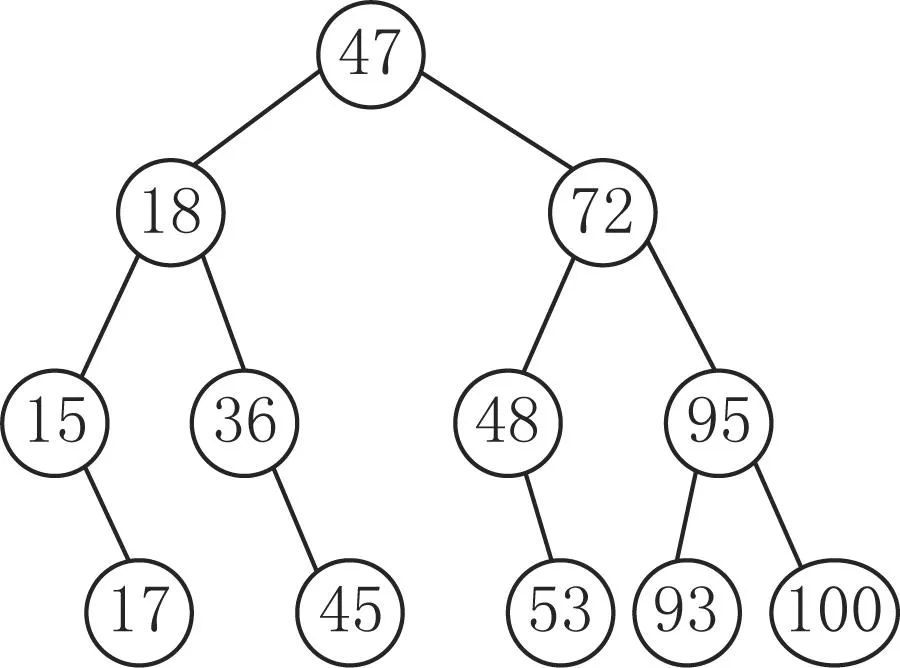
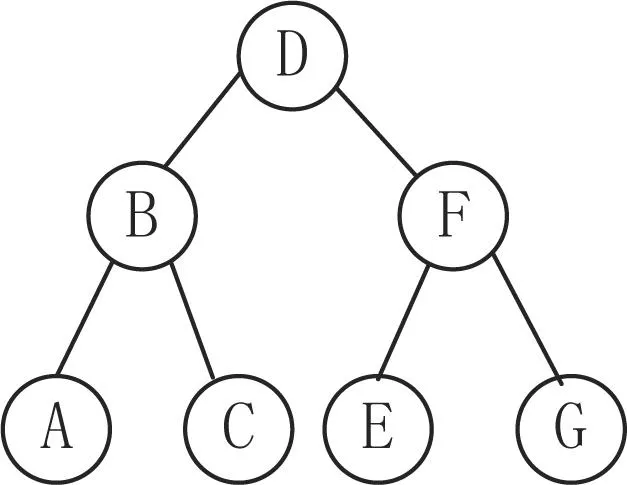
由X=x1x2…xn得到关键字的升序序列Z=z1z2…zn,即z1

因此, 升序序列Z=z1z2…zn与比较次数序列C=c1c2…cn之间存在一对一的关系,即存在一个二分查找函数f,使得

ci=f(Z,zi),i=1,2,…,n.

(1)

进一步对比较次数序列C=c1c2…cn进行升序排序,如果在排序过程中发生ci与cj互换,则zi与zj也进行互换。当比较次数序列C=c1c2…cn变为升序序列时,则此时的Z=z1z2…zn就是一个严格平衡二叉树序列。

在二叉排序中,越早插入的关键字,由于其在二叉排序树的路径越短,从而在二叉排序查找过程中的比较次数也越少,而这与二分查找的比较次数是一致的。因此,根据得到的严格平衡二叉树序列就可以建立关键字的严格平衡二叉树。

3建立严格平衡二叉树的算法

根据建立严格平衡二叉树的原理,为了保证建立的二叉排序树是严格平衡二叉树,需要改变关键字的输入顺序,因为二叉排序树的链式存储结构不光与关键字的大小有关,还与关键字的插入二叉排序树的先后有关。

整个建立严格平衡二叉树的算法步骤可以归纳如下。

第1步通过排序,将一个初始的关键字序列转化为一个关键字的升序序列。不妨设初始序列为X=x1x2…xn,而转化后的升序序列为Z=z1z2…zn。

第2步用二分查找统计升序序列中每个元素zi(i=1,2,…,n)在查找过程中的比较次数ci(i=1,2,…,n),其计算公式见(1)式。

第3步对比较次数序列C=c1c2…cn进行升序排序。如果在排序过程中出现需要ci与cj交换,则相应有zi与zj交换。排序的结果是, C=c1c2…cn是一个升序序列,而Z=z1z2…zn变成一个严格平衡二叉树序列。

第4步在二叉排序树的建立过程中,依次插入严格平衡二叉树序列中的每个关键字,则最终得到严格平衡二叉树。

3.1初始序列的选择排序

对于一个无序的关键字序列X=x1x2…xn，序列中的元素各不相同。为了将其变成一个关键字的升序序列，需要进行的选择排序过程如下：

步0 给出关键字序列X=x1x2…xn。令i=1。

步1令l=i，表示第i个位置需要竞争。

步2令j=i+1，如果xj

步3如果j

步4如果l≠i，则将xl与xi交换，即

xl=min{xi,xi+1,…,xn}.

(2)

步5令i=i+1。如果i

经过选择排序后，X=x1x2…xn变成一个关键字的升序序列。

3.2二分查找统计比较次数

由于无序序列X经过3.1中的选择排序后，已经变成一个关键字的升序序列。因此，接下来就可以用二分查找法依次统计每个关键字的比较次数。统计过程如下：

步0令i=1和cj=0(j=1,2,…,n)。

步1令l=1，h=n。

步3令ci=ci+1。如果xi≠xm，则转步2；否则，转步4。

步4令i=i+1。如果i

3.3严格平衡二叉树序列生成

从生成严格平衡二叉序列的原理可知，该序列的生成完全取决于比较序列C的升序排序。在升序排序过程中，如果出现ci与cj交换，则同时进行xi与xj的交换。具体步骤如下：

步0根据算法3.2，用二分法统计出关键字升序序列X中的每个元素xi的比较次数ci，得到比较次数序列C=c1c2…cn。令i=1。

步1令l=i，表示第i个位置需要竞争。

步2令j=i+1，如果cj

步3如果j

步4如果l≠i，则将cl与ci交换，即

cl=min{ci,ci+1,…,cn}.

(3)

同时将xi与xj交换。

步5令i=i+1。如果i

步6在二叉排序树的非递归建立[6]过程中，依次插入关键字xi(i=1,2,…,n)。

经过上述算法，先通过选择排序生成严格平衡二叉树序列，然后由该序列的非递归插入产生的二叉排序树就是严格平衡二叉树。

4算例测试

本算法使用VC 6.0作为仿真工具，在CPU为3.2 GHz和内存为1.86 Gb的个人台式电脑上完成仿真。

算例1已知关键字序列X={36, 15,18，17，53 ,45 ,48 ,47,72 ,93 ,95，100}。求由该整型关键字序列构成的严格平衡二叉树。

解第一步关键字序列X通过选择排序转化为关键字的升序序列X={15, 17,18，36，45,47,48,53,72,93,95，100}。

第二步元素xi(i=1,2,…,12)在二分查找X过程中的比较次数ci(i=1,2,…,12)如表1所示。

表1二分查找关键字的比较次数

i123456789101112xi1517183645474853729395100ci342341342434

第三步在对比较次数序列ci(i=1,2,…,12)进行升序排序过程中得到如表2所示的关键字序列xi(i=1,2,…,12)。

表2关键字重排结果

i123456789101112ci122333344444xi4718721536489517455393100

第四步根据得表2所示的严格平衡二叉树序列xi(i=1,2,…,12)构造的二叉排序树如图1。

图1　二叉树排序树

显然，图1显示的二叉树排序树是一棵严格平衡二叉树。

算例2已知关键字序列X={C, B,A，G,E，D，F}。求由该字符关键字构成的严格平衡二叉树。

解第一步 关键字序列X通过选择排序转化为关键字的升序序列X={A,B,C,D,E,F,G}。

第二步 元素xi(i=1,2,…,7)在二分查找X过程中的比较次数ci(i=1,2,…,7)如表3。

表3字符二分查找的比较次数

i1234567xiABCDEFGci3231323

第三步比较次数序列ci(i=1,2,…,7)进行升序排序后得到如表4示的关键字序列xi(i=1,2,…,7)。

表4字符重排结果

i1234567ci1223333xiDBFACEG

第四步根据表4所示的严格平衡二叉树序列xi(i=1,2,…,7)构造的二叉排序树如图2。

图2　二叉排序树

同样,如图2所示的二叉排序树是一棵严格平衡二叉树。

5算法分析

笔者设计的算法有两次升序排序:一次是关键字的选择升序排序,该排序是为关键字的二分查找做准备的;另一个是关键字的比较次数的选择升序排序,它是生成严格平衡二叉树序列的关键.需要指出的是，两次排序都是用的选择排序，而且都是升序排序。事实上，这里也可以选择其它任意一种排序方法，而且无论是升序排序还是降序排序都可以。也就是说，可以是下列情形之一。

(1)关键字序列与比较次数序列都是升序。

(2)关键字序列与比较次数序列都是降序。

(3)关键字序列是升序排序，而比较次数序列是降序排序。

(4)关键字序列是降序排序，而比较次数序列是升序排序。

无论采用上述哪种情形,最终都会得到相同的严格平衡二叉树序列,即构造的严格平衡二叉树是唯一的。如果关键字的比较次数序列采用升序排序，即情形(1)或情形(4),则严格平衡二叉树序列是X=x1x2…xn。如果是情形(2)或情形(3),则严格平衡二叉树序列是X=xnxn-1…x1。

6结束语

笔者提出了一种不需要借助栈也可以构造严格平衡二叉树的非递归算法。通过排序算法将关键字序列变为一个有序序列,将其作为二分查找的依据。利用二分查找算法,对关键字序列中的每个关键字进行二分查找的比较次数进行统计。进一步使用排序算法对查找次数序列进行排序,在排序过程中对关键字的相应位置进行调整,排序完后就形成一个严格平衡二叉树序列。最后,通过严格平衡二叉树序列建立二叉排序树,该二叉排序树就是一棵严格平衡二叉树。实验结果表明,利用本文算法进行二叉排序树的建立,能够实现不借助栈也能非递归地建立一棵严格平衡二叉树。

参考文献:

[1]谭浩强.实用数据结构[M].北京: 清华大学出版社,2008．

[2]孙晓辉,王劲林,陈晓.实时系统中的动态内存分配算法[J] .计算机工程 ,2008, 34(8): 80-81.

[3]岑岗,周炳生.严格平衡二叉排序树及其构造[J].计算机工程与应用 ,2005 (13): 57-60．

[4]胡云 ,黄震宇. 一种快速构建平衡二叉搜索树的算法[J] 大庆师范学院学报, 2008，28(2)：20-23.

[5]王防修,周康. 一种构建严格平衡二叉搜索树的非递归算法[J]. 武汉工业学院学报, 2013，32(4)：32-34。

[6]徐孝凯，贺桂英.数据结构(C语言描述)[M].北 京: 清华大学出版社,2008．

A method to establish a strict balance two

fork tree without the help of a stack

WEIZhi-wei，WANGFang-xiu

(School of Mathematics and Computer Science,Wuhan Polytechnic University,Wuhan 430023,China)

Abstract：Because establishment of a strict balanced two binary tree needs the help of the stack, this paper presents an algorithm to establish a strict balanced two binary tree without the help of the stack. In order to search for keywords in half, it needs to sort the existing keyword sequence. It statistics the number of comparision in binary search in the ordered keyword sequence. A strict balanced binary tree sequence will be obtained by the sortion of the times of comparison of the keywords after the statistics. Finally, a strict balance two fork tree is obtained after every keyword has been successively inserted into the two binary sort tree on non recursive insertion algorithm. The results of the examples show that a strict balance two fork tree can also be established without the help of the stack.

Key words：Selection sort; Two binary sort tree; Strict balanced two binary tree; Binary search; Search efficiency

DOI:10.3969/j.issn.2095-7386.2015.04.013

文章编号：2095-7386(2015)04-0051-05

基金项目：2013年国家自然科学 (61201452).

作者简介：刘光蓉(1971-)，女，副教授，E-mail：lgr981009@126.com.

收稿日期：2015-09-14.

中图分类号：TP 391

文献标识码：A