反馈粒子滤波在GPS/INS组合导航系统中的应用

秦　岭，刘晨曦

(武汉轻工大学 电气与电子工程学院，湖北 武汉 430023)



反馈粒子滤波在GPS/INS组合导航系统中的应用

秦岭，刘晨曦

(武汉轻工大学 电气与电子工程学院，湖北 武汉 430023)

摘要：GPS/INS组合导航系统的性能主要是由滤波器的精度和实时性决定，由于组合导航系统的状态维数较高，导致滤波器的计算量大，因而制约了粒子滤波与高斯粒子滤波算法在实际工程中的应用。针对惯性组合导航系统的特点，基于反馈粒子滤波算法，对位置/速度误差进行了滤波估计，同时利用组合滤波器的输出对INS系统的误差进行修正，最后对相应的算法进行了仿真验证。仿真结果表明，与混合高斯粒子滤波算法相比，反馈粒子滤波算法的滤波精度和实时性都有一定的提高。

关键词：组合导航系统；反馈粒子滤波；高斯粒子滤波

1引言

GPS/INS组合导航系统[1]针对GPS和INS的误差特性，采用GPS的位置与速度信息对INS进行周期性校正，有效的减少了系统误差的影响，提高了导航系统的整体性能。目前，常用的信息融合算法是Kalman滤波算法[2]，在理想情况下，Kalman滤波效果较好，但是当载体作大幅度机动或者GPS信号受到干扰或遮挡时，Kalman滤波会产生较大的误差，进而导致滤波失败。基于Monte Carlo采样方法的粒子滤波(Particle Filter, PF)和高斯粒子滤波(Gaussian Particle Filter, GPF)算法可以有效的解决上述问题[3-6]，然而组合导航系统的状态变量维数高，为了提高粒子的采样效率，保证滤波收敛及其精度，必须采用更多数量的粒子来逼近概率密度函数，这就导致计算量急剧增加，制约了粒子滤波和高斯粒子滤波算法在组合导航系统中的应用。为此，文献[4]和[6]采用Kalman滤波分别结合粒子滤波与高斯粒子滤波算法，对组合系统的线性部分采用Kalman滤波进行递推估计，而对系统非线性部分则分别利用粒子滤波与高斯粒子滤波估计，有效的减少了滤波的计算量，加快了滤波的收敛速度。反馈粒子滤波(Feedback Particle Filter, FPF)[7]是一种新型的免重采样非线性滤波算法，它将每个粒子都视为一个能控的随机系统，通过求解Euler-Lagrange方程，得到在K-L距离最小意义下的最优反馈控制律，进而基于每个粒子的自身状态进行校正和更新。由于反馈粒子滤波不需要重采样，因此有效的避免了因估计状态维数的增加而导致的计算量增大，同时反馈粒子滤波实现简单，实时性好，易于工程实际应用。

本文主要对松耦合GPS/INS组合导航系统的位置信息融合进行仿真研究，利用GPS观测信息通过反馈粒子滤波算法修正INS的位置误差信息，以提高导航精度。最后通过算例仿真表明，与混合高斯粒子滤波相比，基于反馈粒子滤波算法的GPS/INS组合导航系统精度较高，实时性较好，可以满足实际的导航要求。

2GPS/INS松耦合滤波模型

取地理坐标系为导航坐标系，则惯性导航系统状态变量定义为：

X(t)=[φeφnφuδveδvnδvuδL δλ δh

εbxεbyεbzεrxεryεrzbxbybzδt]T.

矩阵各元素分别代表坐标系中INS在各方向的平台角度误差、速度误差、位置误差、陀螺仪漂移、一阶马尔可夫过程以及加速度计零漂等，共计18维行向量。同时，由于采用GPS的量测信息作为INS的修正信息，因此将GPS的接收机钟差信息扩充到组合导航系统的状态向量。进而组合导航系统的误差系统状态方程可以表示为：

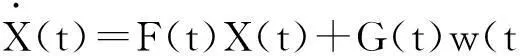
(1)

其中系统动态矩阵F(t)和过程误差系数矩阵G(t)的非零元素详见文献[8]。

将INS的输出位置信息与GPS接收机计算出的相应位置信息进行相减，其差值作为组合导航系统的量测信息，同时将量测噪声看为高斯白噪声，则组合导航系统的量测方程为：

Z(t)=H(t)X(t)+v(t).

(2)

3反馈粒子滤波

假设系统状态方程和量测方程分别为式(1)和式(2)，且估计状态的后验概率密度函数服从高斯分布，即pt～N(x;μt,Pt)，于是反馈增益矩阵Kt可以由Euler-Lagrange方程解得

(3)

并且满足以下边界条件

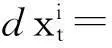
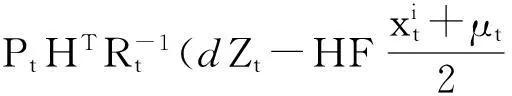
(4)

(5)

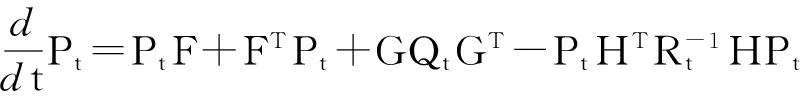
(6)

在算法具体实现时，可以采用样本粒子的均值和方差对其进行估计。即

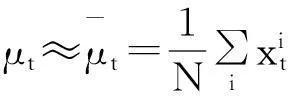
(7)

(8)

此时，对第i个粒子的迭代方程(4)可以改写为：

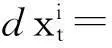
(9)

由此，可以给出基于反馈粒子滤波的组合导航滤波算法步骤如下：

Step2. 假设每次迭代采样时间间隔为Δt，则在从t→t+Δt时，计算一步预测均值，即

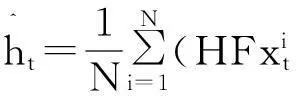
(10)

Step3.对每一个样本粒子分别按下列式子计算新息误差和反馈增益；

(11)

(12)

其中样本粒子的均值和协方差可以分别按式(7)和式(8)进行统计。

Step4随机采样ΔV～N(0,1)，然后对每一个样本粒子按照下式进行校正更新。

(13)

然后令t=t+Δt，返回Step2进行下一次迭代，更新各个粒子值。

4算例与分析

取一组GPS/INS导航数据进行仿真实验。仿真参数设置如下：设惯性导航系统的陀螺随机常值为0.1(°)/h，陀螺仪一阶马尔可夫过程驱动白噪声为0.1(°)/h，相关时间为500 s；加速度计一阶马尔柯夫过程驱动白噪声为1×10-3g，相关时间常数1 000 s。GPS接收机位置白噪声30 m，速度白噪声1 m/s，仿真时间为50 s，采样时间为Δt=0.1 s。

基于Monte Carlo方法的粒子滤波和高斯粒子滤波算法的滤波精度是随着粒子数目的增加而增大的，估计状态的维数越高，需要的粒子数目就越多，滤波算法的计算量也就越大，而反馈粒子滤波算法由于不需要在每次迭代时对粒子进行采样。只需要计算粒子的反馈增益，因此有效的减少了算法的复杂度，在保证滤波收敛的同时也提高了算法的精度。因此，为了评价反馈粒子滤波算法的性能，在仿真中对同一组测试数据分别利用高斯粒子混合滤波算法和反馈粒子滤波算法进行组合导航系统的信息融合，粒子数目分别选取为N=1 000和N=10 000两种情况进行比较。

图1—2给出了1 000个粒子情况下，GPF和FPF算法的位置和速度在各方向的误差曲线图。由图可以看出，GPF和FPF算法的位置误差曲线均能收敛，其中FPF滤波后各个方向的位置误差均减小到约20 m以内，滤波精度明显均优于GPF滤波后各个方向的位置误差。两种算法对于垂直方向的速度误差都是发散的，但是FPF滤波后水平方向的速度误差均减小至1 m/s以内，滤波精度也较GPF更高。同时，表1给出了两种算法在不同情况下的运行时间，由此看出，FPF的实时性也优于GPF，表明FPF在粒子数目较少的情况下，不仅保证了滤波精度，而且提高了导航系统的实时性。

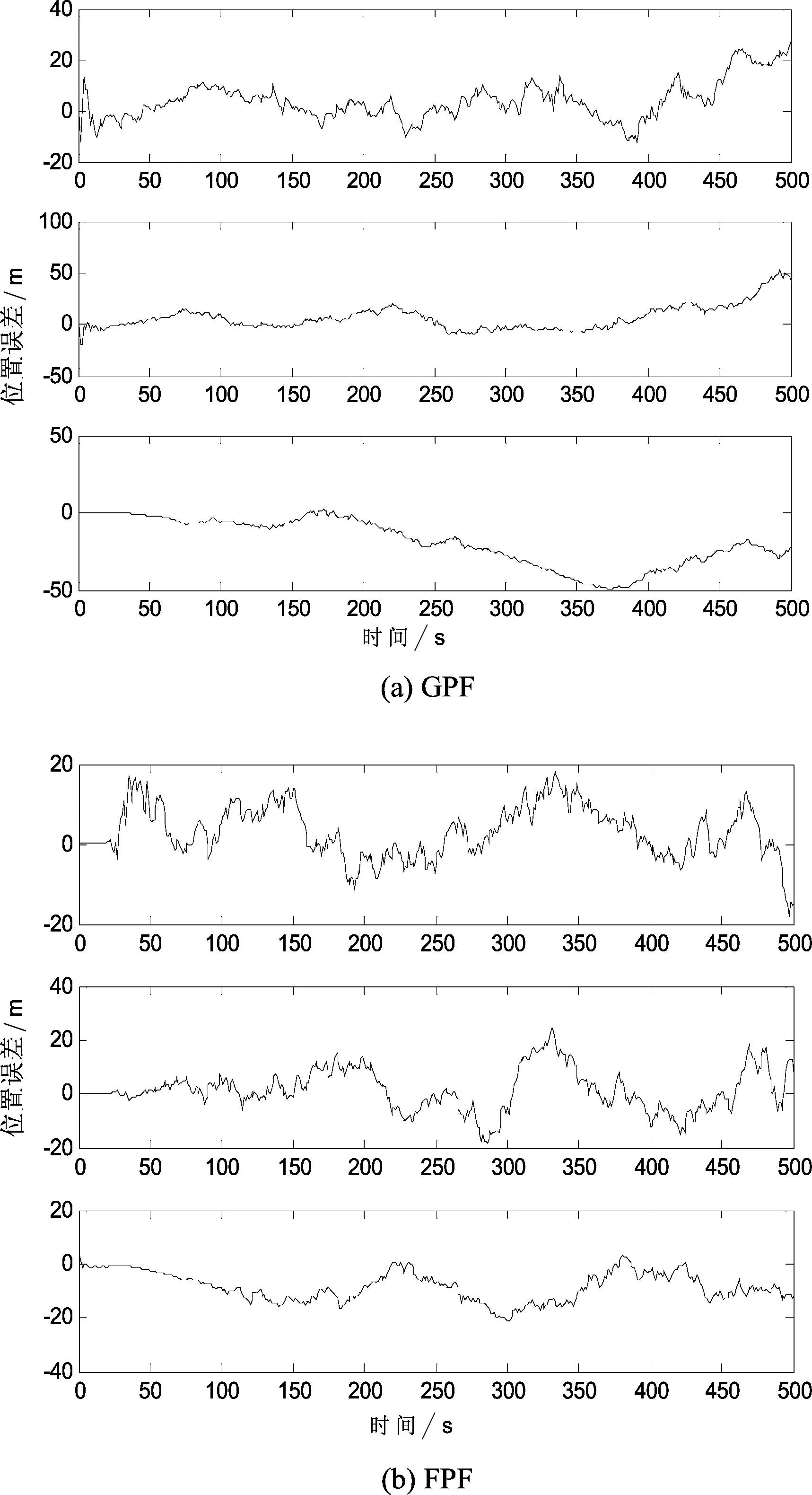
图1　位置误差曲线图(N=1 000)

图2　速度误差曲线图(N=1 000)

图3　位置误差曲线图(N=10 000)

图4　速度误差曲线图(N=10 000)

图3—4给出了10 000个粒子情况下，GPF和FPF的位置和速度在各方向的误差曲线图。由图可以看出，对于GPF，水平方向的位置误差虽然可以收敛至20 m范围以内，但是波动大，精度较差，速度误差也呈现发散趋势。而经过反FPF融合后，组合导航系统的位置误差均能收敛在20 m以内，同时水平方向的速度误差均能减小至1 m/s以内，与GPF相比，曲线变化更为平缓。由此可见，在相同粒子数目的情况下，采用FPF实现GPS/INS组合导航系统的位置和速度信息融合，其误差精度均优于采用GPF滤波算法。并且，当粒子数量减少后，FPF滤波精度虽然有所降低，但是提高了组合系统的实时性。

表1FPF和GPF运行时间比较

数目100010000算法FPFGPFFPFGPF时间/s5.94599918.16729246.891639178.200659

5结论

本文基于反馈粒子滤波算法，对GPS/INS松组合导航系统进行了信息融合。并将滤波结果进行对比分析，仿真结果表明，该方法可以在粒子数目较少的情况下，较为准确的估计惯性导航系统的误差信息，并且随着粒子数目的增加，滤波精度会有所提高，但是实时性降低。与高斯粒子滤波混合算法相比，反馈粒子滤波不需要进行重采样，计算量小，易

于实现，在保证滤波精度的同时，也能有效的克服由于组合导航系统维数过高而导致粒子数目增加滤波计算量增大的缺点，更加适用于组合导航系统信息的实时融合。

参考文献:

[1]Casper E S. INS and GPSintegration[D]. Lyngby: Technical University of Denmark, 2006: 60-72.

[2]鲍其莲,周媛嫒. 基于UKF的GPS/SINS伪距(伪距率)组合导航系统设计[J]. 中国惯性技术学报, 2008, 16(1): 78-82.

[3]周翟和,刘建业,赖际舟,等. Rao-Blackwellized粒子滤波在SINS/GPS深组合导航系统中的应用研究[J]. 宇航学报, 2009(2): 515-520.

[4]袁俊刚,范胜林,刘建业,等. 卡尔曼/粒子组合滤波在GPS/INS组合导航中的应用研究[J].导航与控制, 2010,09(4): 37-40．

[5]周翟和,刘建业,赖际舟,等．混合高斯粒子滤波在组合导航中应用的计算量分析[J]．中国惯性技术学报, 2010, 18(5): 595-599．

[6]熊剑,郭杭,熊智,等. GPS/INS组合导航系统中的高斯粒子滤波混和算法[J]. 中国惯性技术学报,2012,20(2): 225-229．

[7]Yang T, Mehta P G,Meyn S P.Feedback particle filter[J]. IEEE Trans. onAutomatic Control, 2013, 58(10): 2465-2480.

[8]王惠南. GPS导航原理与应用[M]. 北京: 科学出版社, 2003．

Usage of Feedback Particle Filter algorithm in

GPS/INS integrated navigation system

QINLing,LIUChen-Xi

(School of Electrical and Electronic Engineering, Wuhan Polytechnic University, Wuhan 430023,China)

Abstract：The performance of GPS/INS integrated navigation system will directly be determinedby the precision and real-time performance of the filters.The dimension of the integrated navigation system is so high that the filter needs the large amount of computation. The result is that the application of particle filter and the Gaussian particle filter algorithms is restricted in practice. According to the characteristics of integrated navigation system, the errors of position and velocity are estimated based on feedback particle filter.And the use of the integration method allows the integration navigation system correcting the errors of INS. At last the filter algorithm is verified by simulation. The simulation results show that the precision and real-time performance of feedback particle filter can be improved, compared with those of Gaussian particle hybrid filter.

Key words：integrated navigation system; Feedback Particle Filter; Gaussian Particle Filter

基金项目：国家自然科学基金资助项目(61179032).

DOI:10.3969/j.issn.2095-7386.2015.04.016 10.3969/j.issn.2095-7386.2015.04.015

文章编号：2095-7386(2015)04-0065-03 2095-7386(2015)04-0060-05

通信作者：郭宏磊(1964-)，男，博士，教授，E-mail:ghl15186@qliyun.com.

作者简介：徐伟(1990-)，男，硕士研究生，E-mail:673407190@qq.com. 王防修(1973-)，男，副教授，E-mail:wfx323@126.com.

收稿日期：2014-12-05.修回日期：2015-04-16. 2015-11-12.

中图分类号：U 666.1

文献标识码：A