关于修正的q-Baskakov算子的性质研究
徐 阳,胡晓敏,耿 慧
(杭州电子科技大学数学研究所,浙江 杭州 310018)
关于修正的q-Baskakov算子的性质研究
徐阳,胡晓敏,耿慧
(杭州电子科技大学数学研究所,浙江 杭州 310018)
摘要:讨论了修正的q-Baskakov算子的性质,通过计算得到该算子的中心矩,研究了这一算子在不同函数空间中的性质,揭示了这类算子的单调性和逼近性质,推广了q-Baskakov算子的一些结论,从而丰富了修正的q-Baskakov算子理论的内容。
关键词:连续模;q-巴斯卡科夫算子;逼近
0引言
1997年George M.Phillips提出q-Bernstein算子以来,q整数与越来越多的算子相结合,得到了很多逼近效果更好的算子,q-Baskakov算子便是其中很重要的一种。关于Baskakov算子和q-Baskakov算子,已经有很多学者进行了研究,并获得了许多很好的结果[1-5]。文献[1]提出了一类修正的q-Baskakov算子,其逼近效果要优于一般的q-Baskakov算子。本文将继续研究这一算子,得到其单调性质,并拓展其逼近性质的定理。
1相关定义及引理
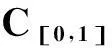
对于函数f(x)∈C[0,∞),文献[1]定义的修正q-Baskakov算子为:

(1)

为了给出本文研究的结果,下面介绍一些概念和辅助引理。


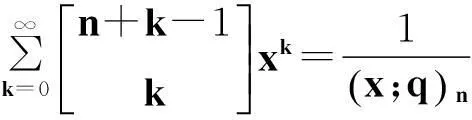
(2)
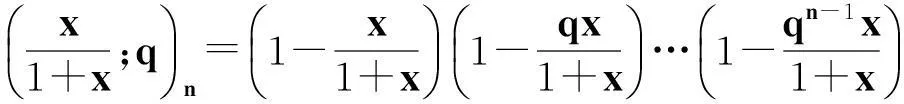
(3)
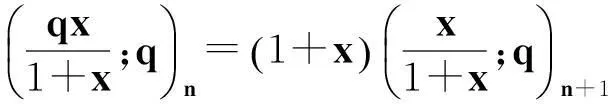
(4)
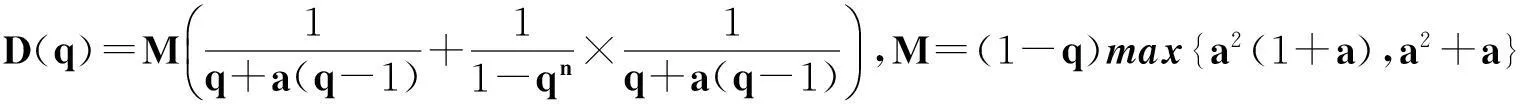
证明根据文献[1]中的得到的该算子的各阶矩,易算出它的中心距,得到此结论。证毕。
2主要结果




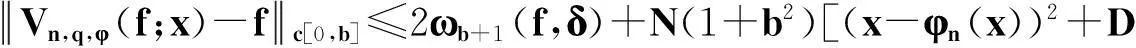
3结束语
本文在文献[1]的基础上,对修正的q-Baskakov算子在两类不同函数空间上的逼近性质进行了研究,推广了Baskakov算子的结论,研究了修正的q-Baskakov算子的单调性,拓展了对修正的q-Baskakov算子的认识,对进一步研究这类修正型的算子有积极意义。
参考文献
[1]莫庆峰,胡晓敏,吴鹏.一类修正的q-Baskakov算子的逼近性质[J].杭州电子科技大学学报,2014,34(4):52-54.
[2]Aral A,Gupta V.On q-Baskakov Type Operators[J].Demonstratio Mathematica,2009,42(1):109-122.
[3]Gupta V,Karsli H.Some approximation properties by q-Szsz-Mirakyan-Baskakov-Stancu operators[J].Lobachevskii Journal of Mathematics,2012,33(2):175-182.
[4]Gupta V,Aral A.Approximation by q-Basakakov Beta Operators[J].Acta Mathematicae Applicatae Sinica(English Series),2011,27(4):569-580.
[5]刘生贵,薛银川.一类Baskakov型算子的逼近性质[J],西南民族大学学报(自然科学版),2006,32(5):893-898.
Research of Properties of Modified q-Baskakov Operators
Xu Yang,Hu Xiaomin,Geng Hui
(InstituteofMathematics,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
Abstract:The modified q-Baskakov operators were studied in this paper.By calculating the operator’s central moment,we investigated some kind of approximation properties of the operators in different function space,and revealed this type of operator’s monotonicity and approximation theorem.Thus generalized the previous results about the operators,and enriched the theory of the modified q-Baskakov operator.
Key words:modulus of continuity;q-Baskakov operators;approximation
中图分类号:O174.41
文献标识码:A
文章编号:1001-9146(2015)05-0098-03
通信作者:
作者简介:徐阳(1991-),女,安徽宿州人,在读研究生,函数逼近论.胡晓敏副教授,E-mail:mathhuxm@163.com.
收稿日期:2014-12-10
DOI:10.13954/j.cnki.hdu.2015.05.021

