风险价值VaR及实证研究

李海燕，曹怀火，潘雪艳

(1. 池州学院 数学与计算机科学系,安徽 池州247000;2. 安徽师范大学 数学计算机科学学院,安徽 芜湖 241003)



风险价值VaR及实证研究

李海燕1，曹怀火1，潘雪艳2

(1. 池州学院 数学与计算机科学系,安徽 池州247000;2. 安徽师范大学 数学计算机科学学院,安徽 芜湖 241003)

摘要：随着经济一体化的深入，风险管理受到各个国家和地区越来越多的重视。本文主要讨论了风险管理中的市场风险度量的方法，具体介绍了基于投资组合的收益(或损失)函数的分布函数提出的风险值(VaR)和期望损失(ES)这两种度量方法，它们是目前使用得最广的市场风险度量方法。文中比较了这两种方法的优缺点，给出了各种不同计算VaR和ES的方法，同时也对各种方法进行了对比讨论，给出了一个基于中国上证沪深指数在1999—2013年的日收益率序列的一个实证研究。

关键词：市场风险，VaR，ES，历史模拟法，蒙特卡罗模拟法，方差—协方差法

1997年的亚洲金融风暴和2008年的全球金融危机使人们深刻地意识到金融风险管理的重要性，意识到一个国家或地区的金融危机对全球金融市场乃至全球经济的危害，这引发了大批学者和投资者对如何度量风险从而对之加以监管的研究[1-3]。

广义上讲，金融风险主要可以分为几大类，即市场风险、信用风险、流动性风险、操作风险和法律风险。

本文主要关注市场风险，主要系统研究风险值(Value at Risk)和期望损失(Expected Shortfall)以及这些度量方法的优缺点。

1市场风险的度量

1.1　VaR的定义及其优缺点

VaR也称风险值或在险价值，它实际上是衡量了一个金融头寸(或资产组合)，在给定的持有期和给定的置信度下由于市场变动可能发生的最大损失。用统计的语言说，VaR是在给定的持有期，预计盈亏(常特指损失函数)分布的分位数。下面给出VaR定义的数学表达式。

定义1VaRα=inf{l∈R∶P(L>l)≤1-α}=inf{l∈R∶FL(l)≥α}

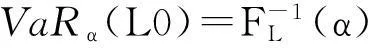
VaR的优点有：对于金融风险管理，它可理解为进入一个风险头寸的资本金要求，并且能通过基于网络的系统直接进行VaR的计算，它已经成为一个标准的风险度量。但也有一些缺点，其中最主要的有：

(1)它忽略了在VaR水平之外的损失，这样就会低估了实际损失；

(2)风险应该满足一致性风险度量公理体系，但VaR不满足其中的次可加性，不是一个相容性风险度量。次可加性就是两个风险组合在一起的总风险应该小于它们单个风险之和，此性质满足资产组合具有风险分散效应的性质。

1.2　ES的定义及其优缺点

为了弥补VaR方法作为风险度量函数不满足次可加性的缺陷，Acebi和Tache(2002)[1]提出了一个新的风险度量方法ES(预期不足又名条件在险价值)，即考虑超过风险值部分的资产收益函数的期望值。

定义2若损失函数L有E(|L|)<∞,分布FL在α水平的预期亏损定义为

ES相比较VaR不仅是一个相容性风险度量，还有另一个优点是在价格出现的波动大时，ES比VaR更能准确地度量金融风险。杨娴、陆凤斌、汪寿阳等[4]对国际有色金属期货市场对VaR和ES风险度量功能进行了比较，另外也有一些其他学者针对其他市场进行了类似的比较。比较的结果也确与理论结果相统一，从而为我国金融机构在选择合适的风险度量作为自己的风险监控工具提供了理论指导和实践论证。

1.3　计算VaR和ES的方法

VaR计算方法的核心在于如何确定资产组合收益(或损失)函数的统计分布或概率密度函数。根据是否对收益(或损失)函数的分布函数给出假设，它的计算方法分为三种：参数估计法，非参数估计法和半参数估计法[5]。

具体的方法有：历史模拟法、蒙特卡罗模拟法以及方差—协方差法等。用方差—协方差法进行讨论应用的比较多，方差—协方差法也是随着学者的研究不断发展完善的。最初人们假定资产收益呈正态分布，实际上，金融数据往往是尖峰厚尾的，因此会低估风险。后来有利用以GARCH模型为核心的GARCH模型族对波动率进行估计从而计算VaR的值，另外又有学者因为考虑极端事件对风险值的影响而将极值理论引入VaR及ES的预测中，还有一些学者利用混合正态模型对最初的计算方法进行了改进。

下面给出VaR和ES的具体计算方法：

(1) 历史模拟法(HS)

HS法是最简单的非参数化的方法，不须对复杂的市场结构做出假设。它的主要思想是假定取样周期中样本收益(或损失)函数的分布函数不会改变，用收益函数的经验分布函数代替收益的分布函数，计算出对应置信水平的VaR和ES值。历史模拟法计算简单，可是这其中隐含假设历史可以重演，显然是与实际情况不相符的。很多极端事件以及突发事件是很难重复的，也有很多以前对收益会有影响的风险因子现在未必会有影响，另外，也可能会有新的风险因子产生影响，这些都是历史模拟法所不能考虑的，因此用此法计算出来的风险值不会超过历史最大值。

历史模拟法作为一种常用的VaR估值的方法，其优点是：简单直观，易于操作，是最简单的非参数方法。但它也有很多缺陷：比如用历史信息并不能预测未来的突发事件，不能提供比样本中最坏损失还要坏的损失值，不能做极端情形下的敏感性测试，等等。

(2)蒙特卡罗模拟法(MC)

蒙特卡罗模拟法又称为随机模拟法，其基本思想是利用风险因子的历史波动参数产生未来风险因子波动的大量可能路径，通过模拟分布可以导出真实分布，预测出VaR值和ES值，这种方法可以很好地处理非线性、非正态问题。

学者们为了提高蒙特卡罗模拟法的计算速度，减少工作量，对该法进行了很多改进，如利用Copula、矩匹配技术、分层抽样技术、重要性抽样技术、条件蒙特卡罗模拟法等等。蒙特卡罗模拟法的基本思想来源于描述法，这种方法保留了描述法中能处理非线性问题及提供风险分布的特点，同时避免了在情形设定时容易出现的随意性和不一致性，可以用来分析各种类型的风险。

(3)方差—协方差法

方差—协方差法在预测VaR和ES值时应用非常多，而且学者们也不断的对此方法进行改进，以便更好的进行预测风险值，为人们的决策提供更准确的参考信息，以便更好地控制风险。

1)传统的方差—协方差法。该方法的核心是：基于对收益(损失)函数分布的方差和协方差矩阵进行估计而得名，也称为分析法或参数法，其假定收益(损失)函数服从正态分布。然后根据已有的样本估计出分布的参数值，得出分布函数，再利用VaR(即分位数)和ES的定义进行计算。

2)基于ARCH、GARCH类方差—协方差法的改进。广义自回归条件异方差GARCH模型是在1982年Engel引入的自回归条件异方差ARCH模型基础上，由Bollerslev[6]于1986年提出的。它主要是针对波动率建模，解决了残差异方差问题，并逐步形成了以GARCH模型为核心的GARCH模型族，大量实证研究表明对大部分金融数据用GARCH(1,1)模拟效果较好。于是很多学者通过利用GARCH类模型对资产收益率的波动率进行建模，从而预测出风险值，为投资者和金融监管机构控制风险提供参考。

3)基于极值理论的方差—协方差法的改进。极值理论主要是考虑极端事件对风险管理的影响，它被广泛应用于水文、保险及风险管理等等。一些学者也将极值理论引入风险度量的应用中，主要考虑到收益(损失)函数的分布很多时候是重尾的，即极端事件对风险值的影响比较大。常用的模型[7]有BMM、POT模型、极值指数理论[8]等等，利用极值理论可以很好的地计极端情况下的风险值。另外，为了在考虑极端情况下更好地对资产收益率的波动率进行建模，也有很多学者将极值理论和GARCH类模型结合起来进行拟合数据[5]，从而计算风险值，如EVT-GARCH模型等等，这方面的文献也非常多。

4)基于混合正态理论的方差—协方差法的改进。为了解决金融时间序列尖峰重尾现象而提出的，一般假设某个分布是由两个正态分布混合构成。将标准正态分布和混合正态分布的密度函数进行对比发现，混合正态分布能很好的捕捉金融数据的重尾性，另外混合正态分布也能用于拟合双峰分布。该方法的核心在于参数估计。

2实证研究

本节我们利用目前银行和投资机构常用的方差—协方差方计算上证指数1999年1月—2012年12月的日对数收益率。首先，将数据分为危机前(1999年1月—2007年12月)和危机中(2008年1月—2012年12月)两部分，分别计算了在不同阶段的VaR和ES。

2.1　数据的描述

首先，根据前面所提及的将数据分为危机前和危机后两部分，由于考虑的计算风险值从而为控制风险提供建议，借鉴通用的处理方法[7]，我们考虑的时间序列是负日对数收益率序列，即rt=100*log(pt/pt-1)，其中pt是第t个交易日的上证指数收盘值。表1给出了该时间序列的一些基本统计量的值

2.2　VaR和ES的估计

这里我们采用方差—协方差法对上证指数收益率序列进行风险估计，从表1可以看出，上证指数收益率存在尖峰厚尾现象，利用正态分布的模型去预测不合适，所以采用t-分布模型去预测它的VaR和ES。

表1　上证指数日对顺收益率危机前和危机中的基本统计量值

由前文的讨论可以知道，在这里VaR和ES的计算公式如下：

其中μ为均值，σ为标准差，α为置信水平，v为t-分布的自由度，g为t-分布的密度函数。本文中从实际数据出发选取t-分布的自由度为4。具体的预测结果如表2。

表2　上证指数日对数收益率危机前和危机中的VaR和ES

注：置信水平为95%。

2.3　回测检验

由于受模型中的各种假设、样本的抽取、建模过程的计算和各种随机因素的影响，在实际应用中，各种不同的建模方法所得出的VaR都会与实际风险值有一定的偏差，为了检验预测出的VaR是否是有效的，监管部门和金融机构需要进行回测检验。回测检验的方法有多种，本文采用的是一种基于二项分布的检验方法，这也是一种常用的检验方法。

该检验的具体思想是：实际风险值超过预测值的次数称为试验失败的次数，这里记失败的次数为N,若预测出的VaR是有效的,则N应服从期望为nα、方差为nα(1-α)的二项分布，其中n是样本容量、1-α是置信水平(本文中是95%)。为此，构造检验统计量

则统计量的渐近分布应该是一个标准正态分布。基于统计量z对表2中的VaR值进行检验，结果见表3。

表3　回测检验结果

由表3可以看出，无论是危机前还是危机后，检验统计量的值都在接受域内，由此可以看出以上风险值是可接受的。

3结论

从实证的结果可以看出，在危机前和危机中ES都比VaR要大，这是因为ES是在损失超过VaR的情况下平均损失的值，在市场波动比较大的情况下，ES可能比VaR更可靠些。危机中的VaR(ES)明显要比危机前的VaR(ES)要大，这说明在危机中所面临的风险值要比危机前更大，从而在危机中投资机构应更加谨慎投资，准备足够多的风险准备金，以便在风险发生时可以应对，以避免造成更大的损失。

鉴于以上的实证研究，若简单的只使用VaR作为风险度量指标不是很合适，应该结合ES指标同时使用。尤其是在市场波动较大的时段，采用ES作为风险度量比VaR更可靠，VaR存在低估风险的可能。

参考文献:

[1] 李腊生，刘磊，李婷．基于投资者异质性的投资组合选择与证券市场价格[J].统计研究，2013(2)：40-48．

[2] 李腊生，孙春花．VaR估计中的概率分布设定风险与改进[J].统计研究，2010(10)：40-46．

[3] 王爱民，何信．金融风险统计度量标准研究[J].统计研究，2005(2)：67-70．

[4] 杨娴，陆凤彬，汪寿阳．国际有色金属期货市场VaR和ES 风险度量功效的比较[J].系统工程理论与实践，2011(9)：1645-1651．

[5] 叶青． 基于G A RC H 和半参数法的VaR 模型及其在中国股市风险分析中的应用[J].统计研究，2000( 12)：25-29.

[6] Bollerslev，T．.Generalized autoregressive conditional heteroscedasticity[J].Journal of Econometrics，1986，31：307-327．

[7] Wagner，N．and Marsh，T．A. Measuring tail thickness under GARCH and an application to extreme exchange rate changes[J].Journal of Empirical Finance，2005(12)：85-165．

[8] Hill，J．B．On tail index estimation for dependent heterogeneous data [J].Econometric Theory，2010(26)：436-1398．

[9] Acerbi，C．and D．Tasche. On the coherence of expected shortfall [J].Journal of Banking and Finance，2002(26)：1487-1503．

[10] Engle，R．F．Dynamic conditional correlation—a simple class of multivariate GARCH models[J].Journal of Business and Economic Statistics，2002(20)：339-350．

[11] 李金昌．论统计功能[J].学术月刊，2012(10):82 -90．

[12] 李金昌．政府统计方兴未艾——纪念新中国政府统计机构成立60周年[J].统计研究，2012(8)：33-37．

The Value at Risk and Empirical Analysis

LI Hai-yan1, CAO Huai-huo1, PAN Xue-yan2

(1.Department of Mathematics and Computer Science, Chizhou University，Chizhou 247000, China;

2.School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, China)

Abstract:People are paying more and more attentions to the risk management of the financial market with the economic integration. This paper first introduces the methods of measure market risk, and then gives two important ways: the value at risk (VaR) and the expected shortfall (ES). The advantages and disadvantages of VaR and ES are discussed in this paper. Finally an empirical study of Shanghai Index is presented.

Key words:Market risk， VaR, expected shortfall, history data simulate, Monte Carlo simulate, variance-covariance method

中图分类号：C812

文献标识码：A

文章编号：1007-4260(2015)01-0023-04

DOI：10.13757/j.cnki.cn34-1150/n.2015.01.007

作者简介：李海燕，女，安徽桐城人，硕士，池州学院数学与计算机科学系讲师。

收稿日期：2014-03-29