细分外推与模糊预测在近海水质非线性时序处理中的比较分析

张丽梅，宛立,董建新

(1.大连海洋大学 理学院，辽宁 大连 116023；2.大连海洋大学 海洋与土木工程学院，辽宁 大连 116023;3.山西交通职业技术学院，山西 太原 030031)



细分外推与模糊预测在近海水质非线性时序处理中的比较分析

张丽梅1，宛立2,董建新3

(1.大连海洋大学 理学院，辽宁 大连 116023；2.大连海洋大学 海洋与土木工程学院，辽宁 大连 116023;3.山西交通职业技术学院，山西 太原 030031)

摘要:近海水质非线性时间序列通常由于采集范围大、时间间隔长带有一定震荡性和模糊性，这使得对其进行分析与预测有一定的难度。本研究中以某近海水质指标磷酸盐-P)、硝酸盐-N)、亚硝酸盐-N)、铵盐-N)和硅酸盐-Si)所形成的5种时间序列为例，采用逼近细分模式导出的细分外推法和多参考加权数据的模糊预测法对近海水质时序预测进行了比较分析，并通过图形与误差计算比较了两种方法的异同。结果表明：采用细分外推法预测序列在整体形状上能更好地逼近初始时序，而模糊预测法在整体逼近精度上占有优势。本研究中提出的预测比较方法可为同类问题的预测与模型选取提供参考依据。

关键词:近海水质；细分外推法；模糊预测法

对近海水质监测时，要按照国家海水水质标准设定的监测指标，在采样点进行定时数据监测。监测所得时间序列具有如下三大特点：一是，不同水域、不同时段、不同指标、不同度量标准所形成的时间序列既有一定的波动范围和趋势，又有一定的模糊性；二是，由于数据测量的间隔时间较长，可以将其视为是连续时间序列的离散化表示；三是，由于水域范围大，每次测量值的计算需要对监测点数据进行某种综合，因此，数据会有一定的误差。此外，随着海洋水质监测系统[1]的建立，海洋数据的海量、实时特性都给分析与预测带来更大的困难。鉴于上述特点，对这类序列预测时如果采用经典的ARIMA模型[2-3]方法很难预测序列的震荡性，而采用混沌时间序列的相空间重构方法[4-5]计算又比较复杂且计算工作量大。因此，找到既能反映时间序列整体变化趋势又能很好地反映其震荡性的模型进行建模具有重要的意义。

曲线细分方法[6-7]是计算机辅助几何设计中常用的方法，它通过对初始控制多边形施行一定的细分规则，使得控制多边形不断细化生成光滑极限曲线。细分曲线的光滑逼近性质为构造反映近海水质非线性时间序列整体变化趋势的模型提供了理论依据，本研究中尝试用细分规则反推算，得到细分外推法。模糊预测方法[8-9]在预测带有凹凸性的时间序列时具有良好的特性，在参数选取适当的条件下，它的逼近程度兼顾了时间序列整体以及局部的特征。本研究中通过将细分外推法与模糊预测方法作用于几个典型的近海水质非线性时间序列进行比较分析，期望探究这两种方法在分析近海水质非线性时间序列的可靠性、差异性和适用性。

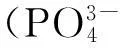
1细分外推法

细分技术是在计算机辅助几何设计和曲面造型中广泛使用的方法。随着细分理论研究的深入和细分技术的成熟，其具有拓扑任意性、表达一致性、可伸缩性、数值稳定性、代码简单性等良好特性，使得其应用越来越广泛。假设有初始控制点列构成的初始控制网格，细分是将细分修改规则作用到初始控制网格上产生新的控制网格，使得新生成的网格不断细化，最终生成光滑极限曲面的过程。细分方法中的细分规则是决定其极限性质的关键因素，而曲面细分规则是由曲线细分规则通过张量积方法获得。时间序列分析仅需曲线细分方法即可，本研究中使用的细分指的是曲线细分方法。而细分又分为插值细分和逼近细分两种，由于逼近细分每次修改不仅产生新的控制点,而且还修改原控制点，通常逼近细分比插值细分更容易达到一定光滑度的要求，故本研究中采用逼近细分模式。

1.1细分规则

二重逼近细分模式参见文献[10]。

(1)

其中，0≤w<1/16，则该细分模式产生的极限曲线具有C2光滑度。

1.2细分外推法

步骤1数据加细。采用细分模式(1)对初始数据进行微调并按规律做数据添加。

(2)

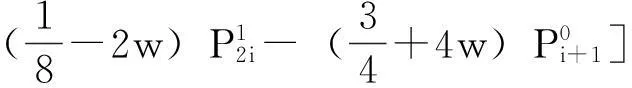
(3)

其中，0≤w<1/16。

由于仍然采用细分模式的公式，所以，光滑性得到有效保持，又由于采用了加细的新点进行外推预测，因此，预测属于小步谨慎预测。

1.3细分外推法的实证分析

2模糊预测法

由于近海水质时间序列具有一定的模糊性，利用模糊时间序列的方法对其进行预测是可行的。Hwang等[8]、Singh[9]对模糊时间序列的使用范围、一般建模原则提出了新方法。Singh[11]从以提高预测精度为出发点的算法改进上进行了研究，给出了有效的建模方法与实证分析，就同类问题的预测精度而言，该算法中提出的预测算法更为有效，故本研究中采用Singh[11]中的预测方法对数据进行预测，具体的算法步骤如下。

(1)构造论域。以可获得的时间序列{Ti}为基础，定义论域U=[Tmin-D1,Tmax+D2]，其中Tmin、Tmax分别为时间序列的最小、最大值，D1、D2为所选取的适合的正整数。根据表1各指标的最大、最小值，对磷酸盐、硝酸盐、亚硝酸盐、铵盐和硅酸盐这5种盐类时间序列构造论域(见表1后两列)。值得一提的是，虽然水质数据监测值不会是负值，但为了预测整体的数学可靠性，给出了适当的负参考值，实际预测时，当预测为负值时，可以以零记。

表1某近海水域5种盐类时间序列的最大、最小值和论域范围值

Tab.1Maximum-minimum and the range of the universe of discourse of the five salt time series collected in coastal water areas

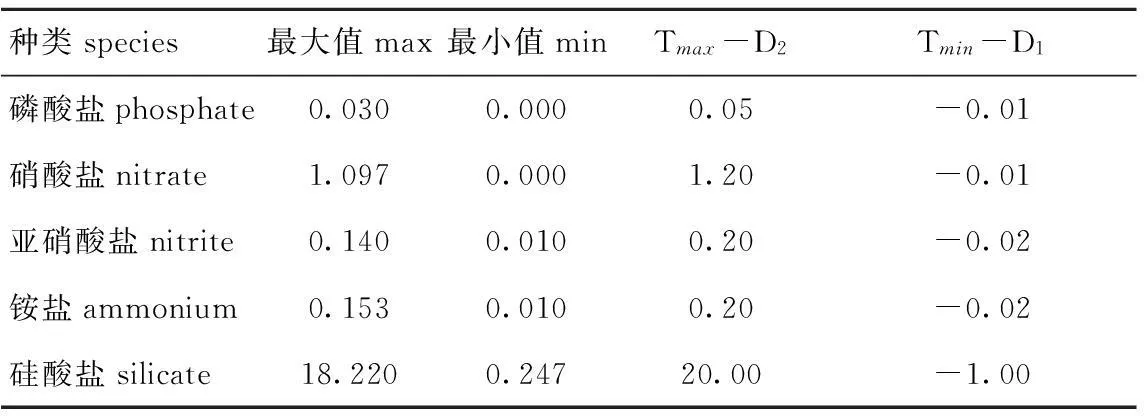
种类species最大值max最小值minTmax-D2Tmin-D1磷酸盐phosphate0.0300.0000.05-0.01硝酸盐nitrate1.0970.0001.20-0.01亚硝酸盐nitrite0.1400.0100.20-0.02铵盐ammonium0.1530.0100.20-0.02硅酸盐silicate18.2200.24720.00-1.00

(2) 划分论域U为等区间。所构造的等区间的个数要与以下要定义的模糊集个数相一致。本研究中构造7个等区间u1～u7如下，设:

t=[(Tmax+D2)-(Tmin-D1)]，

则

(3) 构造7个模糊集A1、A2、A3、A4、A5、A6、A7。模糊集的隶属度函数按如下方式定义：

A1= 1/u1+0.5/u2+0/u3+0/u4+0/u5+

0/u6+0/u7，

A2= 0.5/u1+1/u2+0.5/u3+0/u4+0/u5+

0/u6+0/u7，

A3= 0/u1+0.5/u2+1/u3+0.5/u4+0/u5+

0/u6+0/u7，

A4= 0/u1+0/u2+0.5/u3+1/u4+0.5/u5+

0/u6+0/u7，

A5= 0/u1+0/u2+0/u3+0.5/u4+1/u5+

0.5/u6+0/u7，

A6= 0/u1+0/u2+0/u3+0/u4+0.5/u5+

1/u6+0.5/u7，

A7= 0/u1+0/u2+0/u3+0/u4+0/u5+

0.5/u6+1/u7。

(4) 多参考数据加权进行预测计算。设Ti为时间序列的实际值，当某数据值落入某uj区间时，就对应模糊集Aj。记

Di=‖Ti-Ti-1‖，

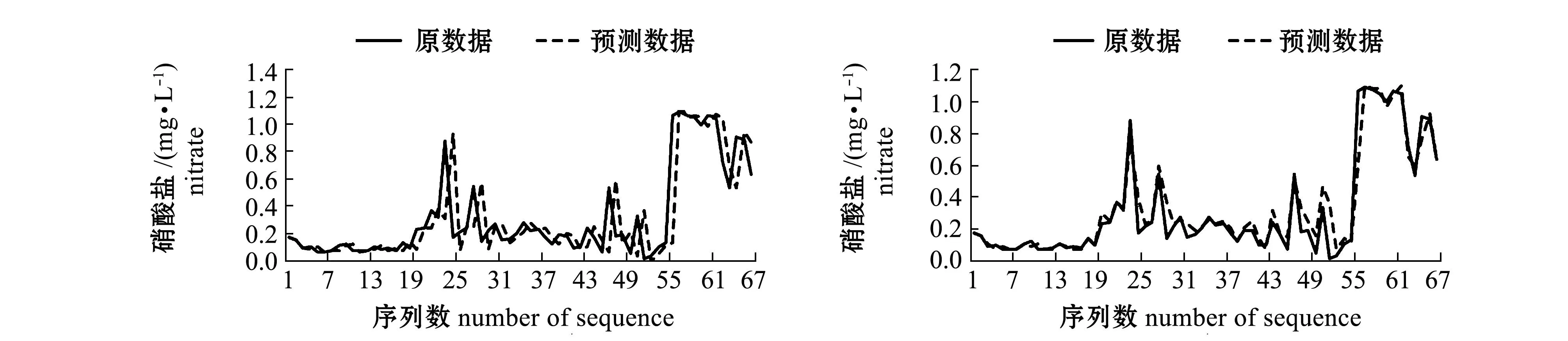
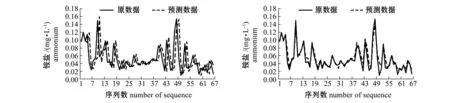
图1　采用细分外推法和模糊预测法对磷酸盐、硝酸盐、亚硝酸盐、铵盐和硅酸盐预测的初始序列和预测序列Fig.1　Initial sequences and forecast sequences of phosphate, nitrate, nitrite, ammonium, and silicate by the subdivision extrapolation and the fuzzy forecasting

3对预测结果的比较分析

3.1方法比较

细分外推法是对待预测值之前的3个初始值，利用细分能产生光滑极限曲线这个理论，采用四点逼近细分模式推导而得。由于细分过程始终关注邻近点的光滑性，因此，预测的整体形状比较好。外推需要一定的基本数据，本例中假设第1层点P1的前4个点与初始点第0层P0的前4个点相吻合，预测是从第5个点开始进行的，图1的左侧图中每个序列的前4个点预测值设定为与初始值相同。为了比较细分外推法与模糊预测法，图1的右侧图也就是模糊预测法也做了同样的处理。

模糊预测法通过构造论域，将论域划分为等区间，构造模糊集的方法进行模糊预测，由于本研究中采用文献[11]中的方法，考虑了多参考数据加权，模糊预测的精度较经典的方法有所提高。通常,论域等分区间的设定要根据实际问题考虑，本研究中，结合模糊预测理论与经验设定区间个数为7，预测结果较好地反映了实际情况。从图形结果看，预测序列与初始序列的逼近效果在个别处有较大差异。预测实验计算显示，预测效果还受论域区间上下限设定的影响以及论域等分区间数的影响。

值得一提的是，由于磷酸盐、硝酸盐、亚硝酸盐、铵盐和硅酸盐这5种盐类时间序列的最小值等于或接近于零，为了更好地从纯数学的角度分析预测效果，论域区间的下限设定为负值，这样能更好地反映预测序列与初始序列的逼近程度，在实际分析时预测为负值的序列值可视为零。

3.2误差比较

为了分析用细分外推法和模糊预测法对近海水质5种盐类时间序列预测的精度，可采用均方误差(MSE)和平均预测误差(APE)进行误差计算。具体计算公式如下：

其中：Δ1为第i个实际值与预测值之差，i=1,2,…,n，n为时间序列中元素个数；Ti为时间序列实际值，i=1,2,…,n。

表2给出了采用细分外推法和模糊预测法对近海水质5种时间序列预测的均方误差和平均预测误差比较结果。其中细分均方误差表示经过细分外推法预测得到的预测序列与初始序列之间的均方误差，细分平均预测误差表示经过细分外推法得到的预测序列与初始序列之间的平均预测误差。同理，模糊均方误差表示经过模糊预测法得到的均方误差，模糊平均预测误差表示经过模糊预测法得到的平均预测误差。由于5种序列各自的最大、最小值有较大差异，所以均方误差仅适合同序列不同方法的比较分析。不同方法作用于这5种序列所得的平均预测误差能反映方法本身的特点。

表2　采用细分外推法和模糊预测法作用于5种盐类时间序列的均方误差和平均预测误差

4结语

本研究中，首先采用曲线逼近细分模式对每组序列进行加细，即针对近海水质时间序列特点通过细分使离散序列平滑加细，然后结合细分特点给出外推计算公式进行预测，同时采用多参考数据加权的模糊预测法对近海水质时间序列进行了预测分析。通过对预测结果效果图分析以及误差计算比较了两种方法的异同，结果显示，在参数选取适当的条件下，采用细分外推法进行分析预测，能够在时间序列的整体形状上更好地逼近初始时序，而采用模糊预测法的误差计算结果显示，在整体逼近精度上该方法占有优势。但对综合运用多种方法进行预测并未提及，对原数据的预处理比如平滑处理可以更好地运用细分方法等，在这些方面也有很大的改进空间，有待于今后在实际预测时综合参考。

参考文献：

[1]曹立杰,郭戈,靳玉峰,等.基于传感器网络的海洋水质监测及赤潮预报系统的设计[J].大连理工大学学报,2014,29(6):664-668.

[2]Jonathan D C,Chan K S.时间序列分析及应用[M].北京:机械工业出版社,2010:145-152.

[3]王振雷,唐苦,王昕.一种基于D-S和ARIMA的多模型软测量方法[J].控制与决策,2014,29(7):1160-1166.

[4]蒋爱华,周璞,章艺,等.基于相空间重构离心泵基础振动的研究[J].农业工程学报,2014,30(2):56-62.

[5]张颖超,刘玉珠.基于相空间重构的神经网络月降水量预测方法[J].计算机仿真,2014,31(1):352-355.

[6]Zorin D,Peter S.Subdivision for modeling and animation[EB/OL].[2000-12-06].http://mrl.nyu.edu/～dzrin/sig00curse/.

[7]Dyn N.Subdivition scheme in computer-aided geometric design[J].Advances in Numerical,1992,2:36-104.

[8]Hwang J R,Chen S M,Lee C H.Handing forecasting problems using fuzzy time series[J].Fuzzy Sets and Systems,1998,100:217-228.

[9]Singh S R.A computational method of forecasting based on high-order fuzzy time series[J].Expert Systems with Applications,2009,36:10551-10559.

[10]张丽梅.细分方法的构造及其应用[D].大连：大连理工大学，2004.

[11]Singh S R.A computational method of forecasting based on fuzzy time series[J].Mathematics and Computers in Simulation,2008,79:539-554.

Comparison of nonlinear times series of water quality analysis in

coastal waters by subdivision extrapolation and fuzzy forecasting

ZHANG Li-mei1, WAN Li2，DONG Jian-xin3

(1.College of Sciences, Dalian Ocean University, Dalian 116023, China； 2.College of Marine and Civil Engineering, Dalian Ocean University, Dalian 116023, China;3.Shanxi Traffic Vocational and Technical College，Taiyuan 030031, China)

Abstract：Usually the nonlinear times series of water quality in coastal waters has uncertainty on analysis and prediction due to certain vibration and fuzziness caused by wide range collection and large interval.-Si) sampled in coastal waters was conducted by subdivision extrapolation, derived from the approximating subdivision scheme, and fuzzy forecasting with much weighted reference data. The comparison of similarities and differences between the two methods through graphics and error calculation revealed that the subdivision extrapolation showed good forecast sequence close to the initial sequence on the whole shape. The fuzzy forecasting method had the advantage of integral approximation accuracy. The findings provide the reference for the solution of the similar prediction and model selection.

Key words：water quality in coastal waters; subdivision extrapolation method; fuzzy forecasting method

作者简介：张丽梅(1965—)， 女，博士， 教授。E-mail:zlm@dlou.edu.cn

基金项目：辽宁省科技计划项目(2012216012)

收稿日期：2014-11-29

中图分类号：O213.2；X55

文献标志码：A

文章编号：2095-1388(2015)03-0324-06

DOI：10.16535/j.cnki.dlhyxb.2015.03.017