我国高精度地心坐标框架确定方法研究
张 鹏,李志才,孙占义,王 凡,陈现军
(1. 国家基础地理信息中心,北京 100830; 2. 导航与位置服务国家测绘地理信息局重点实验室,北京 100830)
Research on Determining High Precision Geocentric Coordinate Reference
Frame in China
ZHANG Peng,LI Zhicai,SUN Zhanyi,WANG Fan,CHEN Xianjun
我国高精度地心坐标框架确定方法研究
张鹏1,2,李志才1,2,孙占义1,2,王凡1,2,陈现军1,2
(1. 国家基础地理信息中心,北京 100830; 2. 导航与位置服务国家测绘地理信息局重点实验室,北京 100830)
Research on Determining High Precision Geocentric Coordinate Reference
Frame in China
ZHANG Peng,LI Zhicai,SUN Zhanyi,WANG Fan,CHEN Xianjun
摘要:基于我国现有国家GNSS连续运行基准站数据资源,提出了实现我国区域地心坐标框架的方法,重点解决了数据处理过程中分区处理的方法和策略。首次提出了将国家基准站分成7个区域进行单天解处理,再进行联合平差的策略,以获得高效、快速的数据处理结果。将区域结果与全球结果进行联合平差,给出选取全球和我国区域框架点的原则,在此基础上对单天解解算结果进行坐标参考框架转换,得到稳定可靠的全球和区域解结果,实现我国地心坐标框架的精确确定。
关键词:地心坐标框架;基准站;数据处理;联合平差
一、引言
建立和维持高精度、三维动态的国家地心坐标参考框架是国家测绘地理信息局的一项重要任务。我国从2008年7月1日起正式启用2000国家大地坐标系统(CGCS2000)作为国家法定的坐标系,作为我国新一代的平面基准。其坐标框架由两部分组成:一是全球导航卫星系统(GNSS)国家级连续运行站网,主要由30个左右的国家级GNSS连续运行基准站网组成;二是国家高精度大地控制网,一共有2542个GPS网点[1]。随着国内经济实力的增强及相关重大项目的组织实施,我国GNSS连续运行基准站总规模已经达到2500站,其中国家级基准站约410个(主要包括基准工程360站及927工程50站),省级基准站约2000个。410个国家级GNSS连续运行基准站均匀覆盖我国陆域国土,将成为维持我国CGCS2000坐标系的主体。考虑到数据处理策略及方法的不同,本文将主要研究基于这410个国家站建立和实现我国区域地心坐标框架的理论方法。
二、总体方法研究
国家地心坐标框架的确定主要涉及GNSS连续运行基准站的数据处理技术。GNSS高精度数据处理技术已日益成熟,相关的国际组织基于全球分布的IGS站完成了ITRF2000、2005、2008的全球框架实现工作[2-4]。本研究将立足于成熟的GNSS数据处理技术,基于数据处理的连续性、可靠性、稳定性等进行区域地心坐标框架的研究工作,重点包括数据预处理、单日数据处理和平差计算3大部分。其中数据预处理的目的是确保数据标准、规范、质量可靠,剔除错误信息等。单日数据处理主要由每站每日的GNSS载波相位观测量计算获得测站和卫星轨道的单日区域松弛解,给出区域测站、极移和卫星等参数的松弛解和方差-协方差矩阵,是下一步平差的准观测值,由于牵涉大网处理,将提出切实可行的分区处理方案。网平差是区域框架实现的最终步骤,将对区域结果与全球结果进行联合平差,根据一定原则研究选取全球和我国区域框架点,在此基础上对自由网解算结果进行坐标参考框架转换,得到最终的全球和区域解结果。
三、数据预处理
数据预处理的目的是数据格式标准化、数据质量检查、数据错误校验等。数据处理主要采用基于观测量的双差处理模式,当基准站多路径较大或其他原因造成数据质量不好时,可能会影响其他基准站的解算成果,因此需对原始观测数据进行检查。利用TEQC软件,可检查评估观测数据多路径效应及周跳数,如MP1或MP2大于0.5,需根据具体情况分析判断该站是否进入下一步数据处理流程。
GNSS高精度数据处理时需根据测站信息文件获取基准站的接收机型号及固件版本号,并据此判定每个通道的观测数据类型。高精度数据处理时还需考虑天线相位中心改正模型,不同的相位中心改正模型可能造成厘米级的定位误差。为避免上述误差的出现,提高定位的精度,每日的计算中需要检查的测站的头文件信息主要包括:测站信息正确性的检验,如测站点名一致性与正确性;接收机与天线型号的信息检查;天线高量取的正确性检查,以及天线高归算至相对应的参考位置检查。
四、单日数据处理
单日数据处理主要由每站每天的GNSS载波相位观测量计算测站位置、接收机钟差与卫星钟差、GNSS卫星轨道参数、大气延迟参数、地球定向参数EOP等多种未知数。在解算中对各参数都给予了松弛的约束,最终获得测站和卫星轨道的单日区域松弛解,该单日解给出了区域测站、极移和卫星等参数的松弛解和方差-协方差矩阵,是下一步平差的准观测值。
1. 数据处理模型策略
GNSS定位精度的提高源于两个方面:一方面是卫星系统的改进、完善和接收技术的进步;另一方面是数据处理中所涉及的各种模型的精化和地球参考框架的改进。在数据处理中,误差的消除或减弱通常采用模型改正或附加参数估计的方法。随着卫星对地观测技术的发展,以及对GNSS定位误差源的认知不断深入,这些模型和方法经历着一个不断完善和精化的过程。在GNSS数据处理中,每一个方法、模型和框架的改变都会对定位结果产生影响,为了减少这些对定位结果的影响,应尽可能采用更准确的物理模型。
卫星轨道采用轨道松弛模式,在估算测站位置的同时, 还允许卫星轨道(IGS精密星历)和地球自转参数(Bull_A)有微量的调整,同时参数估计卫星天线的径向偏差。
大气折射模型采用SAAS模型[5]计算对流层天顶的干、湿延迟分量的初始值,同时每个测站每2个小时估计1个天顶延迟参数,气象数据由GPT模型[6]获得,映射函数采用GMF模型; 同时还对每个测站的东西向和南北向各附加一个大气水平梯度参数估计。
数据处理中采用的地球重力场、固体潮和极潮模型都遵循IERS2003规范[4]。海潮引发的测站地壳形变改正采用最新的全球海潮模型FES2004[4],并同时顾及海潮导致的地球质心变化。
综上所述,对大肠癌合并糖尿病围手术期患者实施肠外营养支持及综合护理干预,能缩短患者进食及排气时间,有利于控制血糖稳定,对患者愈合具有重要意义,值得临床应用。
观测量的随机模型:数据的观测误差主要源于信号的多路径效应和大气对流层的折射误差,这些误差是与卫星的截止高度角密切相关的,为此采用了依据卫星截止高度角确定观测误差的随机模型方法,即数据误差为卫星截止高度角的函数,函数系数由数据验后残差拟合确定。
2. 子网划分策略
由于全球及全国每日需要联合处理的站数超过400站,考虑到软件数据处理能力,本文提出将全球、中国大陆测站划分为不同子网分别处理,然后通过公共联系点绑定在一起。因此,针对数据软件单日处理能力,提出以下子网划分方案:
综合考虑中国大陆板块分布、国际及国内早期GNSS基准站点地理位置和站点数量,以及国家基准网410个基准站的分布密度,按照东北区、华北区、华中区、华南区、西部区和新藏区划分为6个分区。这样划分的优点是每个分区的基准站分布密度相同,周边相邻IGS和早期地壳网络的基准站分布及数量利用相对合理,每个分区测站数量基本上控制在70~80站。
3. 单日数据处理方案
东北区、华北区、华中区、华南区、西部区和新藏区在单日解算时,每个子网中都加入了子网覆盖区域及周边的地壳网络基准站。地壳网络基准站及20个IGS站形成一个分区,共7个分区,形成单日解h文件(hngcc01、hngcc02、…、hngcc07)。
各子网加入其附近及周边地壳网络基准站主要顾及以下因素:①目前地壳网络基准站经过多年连续观测,已经具备较好的坐标和速度成果,可以实现区域坐标参考框架控制;②建立各子网之间联系,在各子网之间增加公共点,便于后续各子网的合并;③由于地壳网络基准站已知其精确坐标,在解算中对其给予约束,可保证解算过程中能快速、正确解算模糊度,提高解算精度并加快解算速度。
IGS站与地壳网络基准站单独分区的目的是将我国区域解算结果与全球解合并,以实现将解算结果转换到全球坐标参考框架下。各分区站点组成见表1。
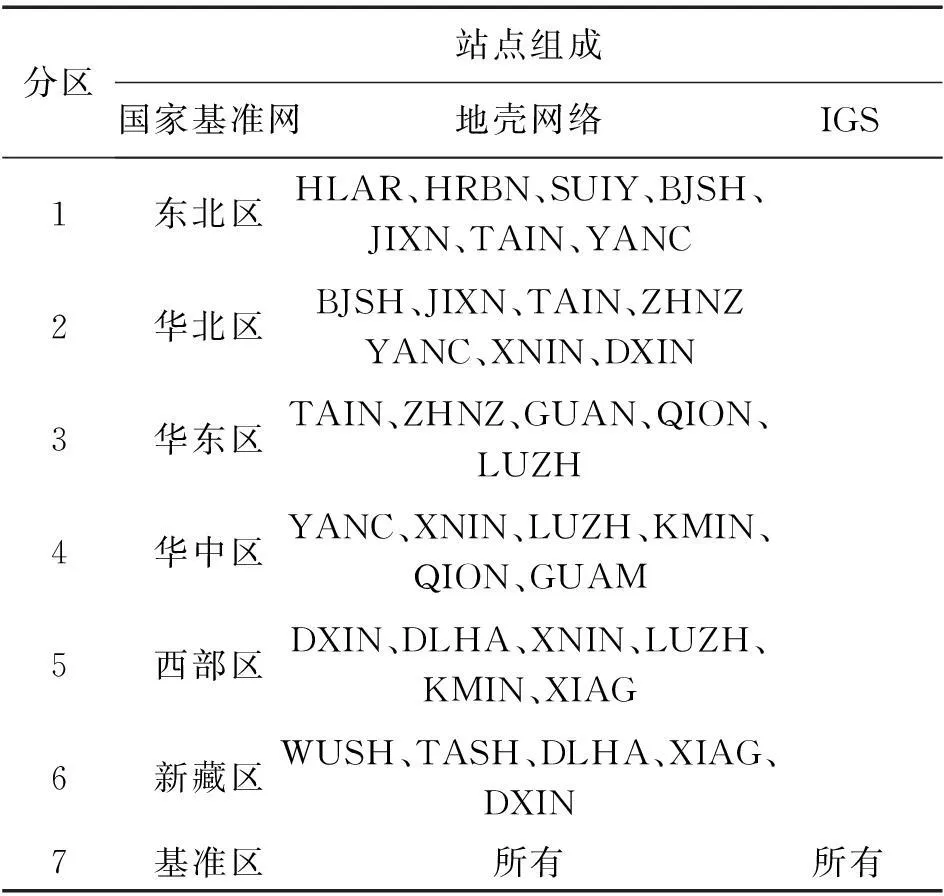
表1 各分区站点组成
五、整体平差计算
利用相应软件将圣地亚哥海洋研究所轨道中心(SOPAC)产出的全球IGS跟踪站的7个单日松弛解(IGS1—IGS7)和每天的各个子网单日松弛解文件通过公共参数(公共测站位置参数和卫星轨道参数)进行合并,得到一个包含所有IGS测站、基准网测站、极移和卫星参数的松弛解及方差-协方差矩阵,即每日整体单日松弛解。整体单日松弛解是下一步平差计算的准观测值。
整体单日松弛解中保持了整网内部测站之间相对位置的准确性,类似无基准的自由网解,再通过参考框架的实现,即可得到全球框架下站点坐标时间序列。
1. 全球框架站选取
为得到国家GNSS基准站点在ITRF2008框架下的坐标和速度,需要对全球框架站点的选取进行合理、严密的分析。在平差中拟选取92个国际站作为框架站,选取步骤为:首先利用站点时间序列等资料按照一定标准对各台站的数据质量进行分析,并对测站进行初步筛选;其次利用七参数法对初选台站进行精选;然后对精选的测站进行监督分类;最后采用分级栅格化的方法使台站在全球的分布符合均匀化的原则。
2. 平差策略
整网采取无约束平差,即平差过程中对站点和卫星均采用松弛约束,进行“无基准”平差。实现参考框架的方法有约束法和相似变换法。
采用约束法需要比较清楚地了解参考点的实测精度,即参考点的实测结果与ITRF或其IGS实现的基准值间的差异,并以此对参考点的位置和速度参数施加约束。不合理的约束将导致GNSS站点间的相对位置关系发生畸变,而且这种畸变与参考点的分布相关,即距参考点越近的地方畸变越大。约束法通常适用于独立的区域性应用(该区域只有少数参考点)或速度基准的确定。
相似变换法是目前更通行的方法,不仅能够完全维持GNSS站点间的相对关系不变,而且还能很好地消除地表质量再分配所导致的地球质心的变化。因此,本方案设计选择七参数的相似变换方法实现参考框架,即通过全球框架站求取整体单日松弛解到ITRF2008框架下的七参数,单日松弛解经过七参数变换,实现整体平移、旋转、缩放至ITRF2008框架基准下。
3. 国家GNSS连续运行基准站网平差
进行整网的无约束平差,即平差过程中对站点和卫星均采用松弛约束,利用序贯卡尔曼滤波,允许每一个单日松弛解有整体的平移、旋转和缩放,同时允许测站位置有随机漫步噪声,将无约束平差结果旋转至ITRF2008框架中。ITRF2008框架是通过用已选取的全球分布的多个IGS站为框架站实现的,框架站点的控制信息采用IERS发布的相应站点在ITRF2008框架下的坐标与速度值。
此外,本研究重点是实现我国的区域地心坐标框架成果,提供我国CGCS2000坐标系下的基准站坐标时间序列,具体实现原理及方法同上。CGCS2000框架通过我国周边及内部20个IGS基准站及地壳网络基准站实现,框架点的控制信息采用CGCS2000下的坐标及速度值。
六、基准控制及精度统计分析
1. 单日解数据处理精度
单日数据处理结果的计算质量可以用NRMS值来评定,通常认为NRMS约为0.25周时,解算结果较合理。NRMS过小,表明解算时给予的约束过松;NRMS大于0.5,表明解算时可能有整周模糊度固定错误或存在其他模型参数解算错误等问题。以2012年中国大陆构造环境监测网络260站数据处理为例,每日解算结果的NRMS值在0.20周以下(如图1所示),说明单天解的计算精度较好,精度均符合要求,可以作为下步网平差的基础。
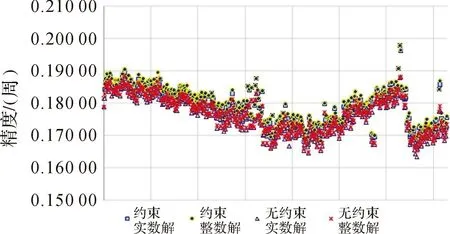
图1 2012年度单天解数据处理精度统计
2. 网平差数据处理精度
对平差结果精度的综合分析是保证数据处理成果可靠性的重要方法,通常用来衡量结果精度的重要指标是单日解基线或坐标重复性。利用该模型计算陆态网络260站2011—2013年的平差结果,相应的精度统计见表2。从表2可以看出,计算精度基本在1 cm以内,说明平差的精度非常高,可基本满足要求。

表2 陆态网点坐标平差精度 mm
七、结束语
本文基于我国现有国家GNSS连续运行基准站数据资源,提出了实现我国区域地心坐标框架的方法,重点解决了数据处理过程中分区处理的方法和策略。首次提出将国家基准站分成7个区域进行单天解处理, 再进行联合平差的策略,以获得高效、快速的数据处理结果。将区域结果与全球结果进行联合平差,给出选取全球和我国区域框架点的原则,在此基础上对单天解解算结果进行了坐标参考框架转
换,得到了稳定可靠的全球和区域解结果,实现了我国地心坐标框架的精确确定。
参考文献:
[1]陈俊勇. 中国现代大地基准——中国大地坐标系统2000(CGCS2000)及其框架[J]. 测绘学报, 2008, 37(3): 269-271.
[2]ALTAMIMI Z, COLLILIEUX X, MÉTIVIER L. ITRF2008: An Improved Solution of the International Terrestrial Reference Frame[J]. Journal of Geodesy, 2011, 85(8): 457-473.
[3]ALTAMIMI Z, COLLILIEUX X, LEGRAND J, et al. ITRF2005: A New Release of the International Terrestrial Reference Frame Based on Time Series of Station Positions and Earth Orientation Parameters[J]. Journal of Geophysical Research, 2007, 112(B909401).
[4]PETIT G, LUZUM B. IERS Conventions (2010)[R]. Frankfurt: IERS, 2010.
[5]SAASTAMOINEN J. Contributions to the Theory of Atmospheric Refraction. Part II. Refraction Corrections in Satellite Geodesy[J]. Bulletin Géodésique, 1973, 107(1): 13-34.
[6]BOEHM J, NIELL A, TREGONING P, et al. Global Mapping Function (GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters, 2006, 33(7): L07304.
[7]陈仲怀,廖超明,宋传峰,等.基于PPP的CGCS2000坐标计算方法研究[J].测绘通报,2014(2):10-12.
[8]王志杰,王庆,毕飞超.大范围区域内地心坐标系与参心坐标系的格网转换方法[J].测绘通报,2013(10):1-4.
[9]BOEHM J, SCHUH H. Troposphere Gradients from the ECMWF in VLBI Analysis[J]. Journal of Geodesy, 2007, 81(6): 403-408.
[10]茹仕高,李倩霞.面向智慧城市的空间坐标系统维持与转换[J].测绘通报,2015(2):19-22.
作者简介:张鹏(1973—),男,博士,教授级高级工程师,研究方向为大地测量与卫星导航。E-mail:zcli@nsdi.gov.cn
基金项目:国家863科技计划(2013AA122501);国家自然科学基金(41274030);国家测绘地理信息局公益性行业专项(201512001)
收稿日期:2014-10-26; 修回日期: 2015-04-05
中图分类号:P226
文献标识码:B
文章编号:0494-0911(2015)12-0001-04
引文格式: 张鹏,李志才,孙占义,等. 我国高精度地心坐标框架确定方法研究[J].测绘通报,2015(12):1-4.DOI:10.13474/j.cnki.11-2246.2015.364

