基于多元模糊推理的空间分类匹配模型研究

李进强，王会珠

(1. 闽江学院地理科学系，福建 福州 350108； 2. 清华山维新技术开发公司， 北京 100084)

Research on the Spatial Classification Matching Model Based on

Fuzzy Reasoning Rules

LI Jinqiang，WANG Huizhu



基于多元模糊推理的空间分类匹配模型研究

李进强1，王会珠2

(1. 闽江学院地理科学系，福建 福州 350108； 2. 清华山维新技术开发公司， 北京 100084)

Research on the Spatial Classification Matching Model Based on

Fuzzy Reasoning Rules

LI Jinqiang，WANG Huizhu

摘要：空间分类匹配是智能GIS研究领域的热点问题，具有重要的理论和实践意义。本文深入分析了现有匹配技术的不足，提出了基于模糊推理规则进行空间分类匹配的通用算法框架，并重点解决了指标集的“模糊隶属度”转化问题，对其正确性和实用性在ArcGIS 9.3平台上进行了验证。

关键词：空间分类匹配；模糊推理；GIS

一、引言

空间分类匹配是智能GIS的核心技术之一, 可广泛用于空间数据库更新、多源空间数据集成、多尺度空间数据库变化信息发现与同步分发等方面，受到业界高度关注。

1. 空间分类匹配研究现状

所谓空间分类匹配，是通过分析两个数据集(新旧版本)中空间目标的差异与相似性，识别出不同数据集中表达现实世界同一地理要素的空间目标，确定不同时期、不同尺度的同名地物是否发生变化[1]。

(1) 空间匹配流程分析

1) 确定集候选：在待匹配的两个数据集中，以其中一个作为参考,在另一个数据集中作空间查询，得到待匹配的候选对象集。

2) 计算评价指标：如几何相似度(形状、位置、方向、长度或大小等)、空间关系相似度、语义相似度等。

3) 多指标合成：即综合语义、几何、拓扑等多个匹配指标。一种做法是顺序使用各种匹配指标，排除一些不可能目标，这种策略需要为每一个指标确定一个阈值，且匹配结果可能与匹配顺序有关。另一种做法是对评价指标进行综合计算,得出结论。显然，第二种方法更加科学合理。

(2) 研究现状分析

① 评价指标研究现状

形状相似度计算是几何评价指标计算中的难点，目前已有许多研究成果，如Hausdorff距离、Fourier描述子[2]、夹角链码法[3]、正切空间(转向角函数法)[4]、最大基因组比对法等，位置和方位指标可通过计算图形的二阶不变矩[5]或进行趋势分析得到，这些方法侧重点各不相同。

在空间关系计算方面，Egenhofer等提出的九交模型来描述实体与实体之间的拓扑关系[6]。丁虹在Egenhofer和AI-Taha基础上建立了面的8种拓扑关系的差异矩阵[7]，确定拓扑关系的强弱程度。张桥平等在Winter形态距离(morphological distance)概念上，提出了针对不同数据源的面目标(集)模糊拓扑关系[8]。

由于语义匹配在很大程度上依赖于属性数据结构及属性信息的完整性，往往缺少唯一标识的属性数据[1]，或由于说明文件的缺失等导致语义理解困难，语义相似度计算失去实用性。

② 多指标合成研究现状

Walter & Fritsch 提出基于概率统计的匹配方法，通过区域统计确定匹配阈值，最后利用信息论的优势函数确定匹配结果。童小华等为克服Walter & Fritsch法计算效率低下的缺点，提出基于理论概率的多指标融合匹配算法[9]，其主要优点是受阈值的影响较小。

熊天星将模糊综合评判引入面实体匹配[10]，综合面质心几何距离法、面实体之间模糊拓扑关系、转向角函数法3种方法。

③ 非一对一匹配模式

赵彬彬等对不同类型(点、线、面)、不同尺度(较大、较小比例尺)空间目标之间的多种匹配模式进行了讨论，并用信息传输模型对1：N、N：1、M：N进行目标相似度计算[11]。

2. 现有研究的不足

从上述分析可以看出，除语义相似度及非一对一匹配模式研究程度不足外，多指标融合模型存在如下问题：

1) 指标体系缺乏系统性，即指标不够全面，或没有从空间匹配的不同角度进行系统考虑。

2) 合成模型理论依据不足，如基于概率的匹配方法，其匹配程度是否符合概率分布,概率值如何计算等。

3) 单一指标可信度和合成权重对匹配结果影响很大，但已有研究大多没有合理的交代。

二、多元模糊推理模型

由于使用不同精度的采集方法、不同的参考系、不同概念/语义模型，以及现实世界时刻发生着变化(人工改造或自然变迁)，使得两个数据集之间存在着不确定性[8]，模糊数学为解决这类问题提供了有效工具。

1. 模糊推理规则

设模糊集U=(u1,u2,…,un),V=(v1,v2,…,vm)，令R为U到V的模糊关系矩阵，R=(rij)n×m，rij表示ui到vj为真的可信度。A=(a1,a2,…,an),B=(b1,b2,…,bm)分别表示U和V的模糊子集，则称模糊变换

B=A·R

(1)

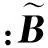
由于涉及多个因素，故又称多元模糊推理。

2. 多元模糊推理匹配模型

(1) 指标集

指标体系的好坏可从如下3个方面考量：

1) 指标的选取要有系统性，即指标集能够从多个角度较全面地反映空间对象的异同。

2) 指标与匹配结果严格相关，即指标越好越能得到肯定的匹配结果。

3) 指标内涵不交叉重复。

重叠度作为预匹配是一个比较好的指标，但其中包含形状、距离、大小、拓扑关系等指标概念交叉。另外，形状越相似，大小越接近，因此不宜同时选用形状相似度和大小相似度。

本文建议采用的指标集见表1。

表1　模糊关系矩阵

(2) 评判集

理论上评判集可包含任意多个元素，但元素太多，易造成模糊关系矩阵太复杂，因此在能够满足要求的前提下，评判集元素应尽可能少，本文取V={A，B，C}，包含3个元素，含义分别是：A表示“匹配”;B表示“不匹配”；C表示“未知”。

(3) 模糊关系矩阵

模糊关系矩阵R 可表示为表1，其中rij表示由U到V为真的隶属度。

三、空间模糊度转化计算

确定模糊关系矩阵(隶属度)是进行模糊推理的关键，下面介绍将指标值转化为模糊隶属度的方法。

1. 形状相似隶属度转化

形状相似度计算一般符合如下规则：

1) 具有平移、旋转不变性，即形状相似度不受平移旋转的影响，缩放因子则可以忽略。

2) 两个要素的形状相似度必须与其匹配程度成严格单调性，即越相似的匹配度越高，越不相似的匹配度越低。

3) 取值在0～1，越接近0越不相似，越接近1越相似，0.5属于最模糊状态。

设形状相似度为x，评判 A、B、C相应的隶属函数分别为μA(x)、μB(x)、μC(x)。因为B是A的补集，因此μB(x)=1-μA(x)；C是表达A/B之间最模糊地带，如果A隶属函数与参数x呈线性关系， μC(x)可表示为μA(x)的三角型隶属关系(如图1所示)， 即有

(2)

图1

2. 空间距离隶属度转化

距离指标可使用空间目标重心之间的欧氏距离，或通过平移旋转将两个空间目标相互对齐，获得平移量，假设δ为空间距离s的标准差(δ可根据采集精度、成图比例尺等因素确定)，本文采用正态隶属度函数模型

s∈[0, 2δ]表示明显支持隶属于同名地物的区域；s∈[3δ,∞]表示明显不支持隶属于同名地物的区域；s∈[2δ, 3δ]是过渡区域, s=2.5δ是最模糊状态，隶属度≈0.5。

μC(s)中心位置μ=2.5δ，参数k尽量接近μA对应的三角型隶属关系。

综合考虑后，得隶属函数如下

(3)

3. 相对方位隶属度转化

公认的8个方位分别为：东、南、西、北、东南、西

北、西南、东北，如图2所示。

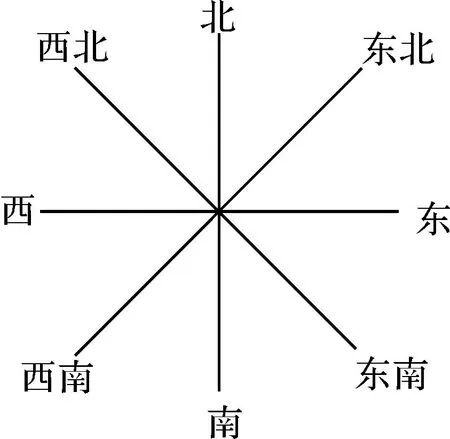
图2

假设T1、T2分别表示待匹配空间目标的方向角，相对方位角可用T=A2-A1进行计算，取值范围为[-90°，90°]。

1) |T|=0°，方位隶属度应等于1。

2) |T|≥45°，因为“东”在[-45°，45°]之间，方位隶属度应等于0。

3) |T|= 22.5°是最模糊的状态，方位隶属度=0.5。

以下三角函数表示的方位隶属度函数恰好满足上述要求

(4)

4. 拓扑关系隶属度转化

丁虹在Egenhofer和AI-Taha基础上建立了8种拓扑关系的差异矩阵确定拓扑关系的强弱程度，差异矩阵从相离(无关)到相等共分为9个等级(0-8)，实质上反映了空间目标是否匹配的可信度。

本文采用模糊层次分析法，将差异矩阵转化为相应的隶属度：

1) 将差异矩阵改造成1—9度重要性正反矩阵，方法是将差异矩阵上三角元素全部+1，使得自身对自身的重要度比为1∶1，然后改写为比例形式，下三角部分取反(见表2)。

表2　重要性正反矩阵

根据文献[8]研究，包含与被包含，往往意味着两空间目标是非同名实体，可能是变更引起的，如房屋拆迁后在原位置重盖。而覆盖和被覆盖，往往说明两空间目标是同名实体，因此，“包含”与“被包含”两列数据没有+1。

2) 按公式 0.5+log81rij将表2转换为模糊互补矩阵。

3) 利用式(5)求取权重向量wi(j=1,2，…，n)

(5)

4) 求隶属度，即μA(j)=wi/max(wi)，同样求μB(j)、 μC(j)。结果见表3。

表3　拓扑关系权值向量与隶属度表

5. 语义相似度隶属度转化

文本型字段相似度采用基于分词的中文文本相似度计算法，数值型字段相似度采用差异距离法，最后将所有字段相似度进行综合求得整体相似度，相应的隶属度函数和前文基本相同。

6. 指标权重的确定

权重向量与应用类型相关，本文针对1∶500空间数据更新，对10位专家进行问卷调查，按“0.5—1.0”标度法统计得出各指标重要性系数，然后采用模糊层次分析法求取权重向量，结果见表4。

表4　指标重要系数表

7. 计算举例

有新旧数据集目标对，评价指标为：u1=0.850， u2=0.624 m(δ=0.2 m 计算)，u3=12°，u4=“相交”，u5=0.777，得到模糊关系矩阵

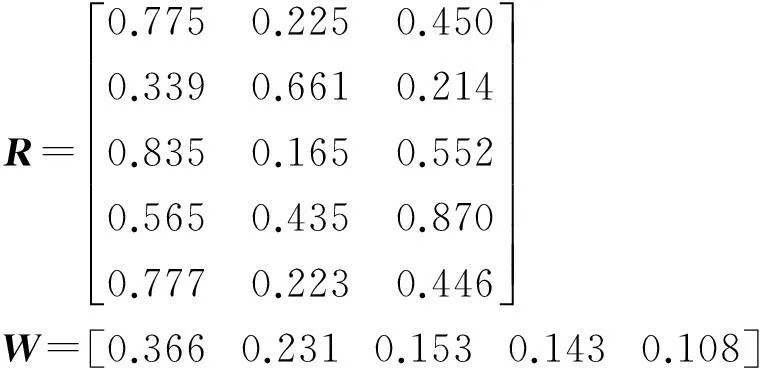
为保留所有信息不被遗漏，采用加权算子进行矩阵合成运算

B=W·R=[0.6540.3470.471]

根据最大隶属度原则，可判定待匹配目标属于同名对象。

四、实例验证

为验证匹配模型的正确性，笔者利用ArcGIS Engine 9.3+Visual C#，开发匹配程序模块，然后挂接到福州市空间资源数据库同步系统上进行验证。

1. 试验环境

同步系统可按指定时间将生产库中的变化信息同步到应用库。本次试验的生产库为1∶500空间数据库，该系统对1∶500数据进行不间断的修测。应用库采用Oracle 9i+ArcSDE 9.3临时搭建，入库数据是福州大学城周边地区，面积约20 km2。

同步系统启动后，先提取1∶500生产库中更新区域的数据，再送交匹配程序与应用库的相同区域进行匹配，最后根据匹配结果对应用库进行更新。以上过程由同步控制器进行控制，每天晚上0点自动执行一次。

2. 匹配指标计算方法

对于自然变迁数据层，形状相似度采用Fourier描述子计算，距离和方位指标采用不变矩法计算；对于人工地物数据层, 形状相似度采用最大基因组比对法进行计算,同时获得距离和方位指标值。拓扑关系采用ArcGIS Engine 拓扑运算接口计算。另外，为简化计算，语义相似度仅考虑变化字段与不变化字段的数量比例。

3. 试验结果

经过分析统计程序连续运行一个月的匹配记录，去除不在有效区域内的内容(16 d)，以及新增地物、消亡地物和未变化的地物，共成功匹配新旧版本同名变化对象：点87个，线230个，面115个，匹配准确率达到91.5%。试验结果表明， 本文提出的匹

配方法针对性强、准确率高，能有效发现新旧版本变化信息，可作为空间数据更新的关键技术。

五、结论与展望

本文采用空间信息科学与模糊集理论相结合的分析方法，对空间分类匹配问题进行深入研究，主要结论如下：

1) 本文基于模糊推理规则，为空间匹配提供了通用的算法框架。

2) 综合运用半经验半理论分析法和模糊层次分析法等，解决了各指标“隶属度”转化问题，使计算模型兼备良好的理论性和实用性。

3) 基于该算法框架，可实现库对库增量变化自动提取，为数据更新、变化率统计提供了理论基础。

本文研究成果在ArcGIS 9.3平台上进行了验证，可为同类型空间数据库更新维护、多源数据融合等人员借鉴和参考。

参考文献：

[1]徐枫，邓敏，赵彬彬，等.空间目标匹配方法的应用分析[J].地球信息科学学报,2009, 11(5):657-663.

[2]王涛，刘文印.傅立叶描述子识别物体的形状[J].计算机研究与发展, 2002, 13(12):1715-1718.

[3]赵宇，陈雁秋.曲线描述的一种方法:夹角链码[J].软件学报, 2004, 15(2):300-307.

[4]付忠良，邵世雄，童春芽.基于正切空间的多尺度面实体形状匹配[J].计算机工程, 2010, 36(17):216-217.

[5]曹明.不变矩在矢量图形识别中的应用[D].大连：大连理工大学，2008：14-16.

[6]EGENHOFER M，AI-TAHA K.Reasoning about Gradual Change of Topological Relationship[J].Lecture Note in Computer Science，1992(639)：196-219.

[7]丁虹.空间相似性理论与计算模型的研究[D].武汉：武汉大学，2004：13-34.

[8]张桥平，李德仁，龚健雅.城市地图数据库面实体匹配技术[J].遥感学报, 2004, 8(2):107-112.

[9]童小华，邓愫愫，史文中.基于概率的地图实体匹配方法[J].测绘学报, 2007, 36(2):210-217.

[10]熊天星.模糊综合评判在面实体匹配中的应用研究[J].长江大学学报, 2013, 10(25):23-27.

[11]赵彬彬.多尺度矢量地图空间目标匹配方法及其应用研究[D]．长沙：中南大学，2011：70-77.引文格式： 张弓同，李四海，焦红波，等. LiDAR点云生成DEM的水面置平方法研究与实现[J].测绘通报，2015(6)：61-64.DOI:10.13474/j.cnki.11-2246.2015.0179

引文格式：李进强，王会珠. 基于多元模糊推理的空间分类匹配模型研究[J].测绘通报，2015(6)：49-52.DOI:10.13474/j.cnki.11-2246.2015.0176

作者简介：李进强(1962—)，男，硕士，教授，主要从事地理空间数据库开发与应用等方面的教学与研究。E-mail：1361639771@qq.com

基金项目：福建省测绘地理信息局2013年科技计划项目(2013M15)

收稿日期：2014-08-27

中图分类号：P208

文献标识码：B

文章编号：0494-0911(2015)06-0049-04