改进SOA算法在焊缝图像分割中的应用

余胜威,丁建明,曹中清

(1.西南交通大学 机械工程学院， 四川 成都 610031;

2.西南交通大学 牵引动力国家重点实验室，四川 成都 610031)



改进SOA算法在焊缝图像分割中的应用

余胜威1,丁建明2,曹中清1

(1.西南交通大学 机械工程学院， 四川 成都 610031;

2.西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

摘要:提出一种基于改进的自适应人群搜索算法(ISOA)的焊缝图像分割方法，该算法通过对基本人群搜索算法的高斯隶属度函数以及隶属度参数计算的改进，自适应确定搜索步长，实现对n尺度图像进行n-1个阈值寻优计算。实验结果表明：对比PSO，GA和SA算法，ISOA算法具有收敛速度快、稳定性强、精度高、全局寻优等特点，有效地克服了传统SOA算法易陷入局部最优和收敛速度慢等缺陷，可满足实际工程需求。

关键词：多尺度分割;ISOA;类方差;PSO;GA;SA

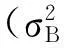
一种阈值寻优的最感性的方法是采用穷举法，基于Otsu的穷举法较简洁，但是计算量大[8]，采用穷举法对本文“car测试图像”进行阈值寻优，当阈值个数为2时，CPU耗时15.41 s，当阈值个数为3时，CPU耗时为4 095.01 s，计算量成千倍增加，采用穷举法对n-1个阈值进行计算，有n(L-n+1)n-1种[7]可能，因此从算法执行效率上考虑，穷举法不适合用于阈值优化分析。然而n-1阈值寻优可转换为一个多尺度的函数优化问题。

本文采用生物智能算法进行图像分割。生物智能算法能够解决传统算法不能解决的问题，如当寻优目标函数是离散的、不可微或者含有一些非线性相关参量时，传统算法根本无法解决。粒子群算法在搜索域内，粒子以一定的速度更新当前最优粒子和最优种群。PSO简单易实现，然而易出现早熟等现象，以致不能全局寻优[10]。遗传算法是一种采用适者生存，优胜劣汰的随机搜索方法，GA直接对结构对象进行操作，不存在求导和函数连续性的限定，但GA存在收敛性差、耗时长等缺点[11]，给图像分割阈值全局寻优带来困难。模拟退火算法(SA)是一种启发式随机搜索算法，通过模拟固体物质的退火过程，克服了穷举法计算量过大的缺点，然而计算量大，Hammouche等研究表明[12]，PSO图像分割在CPU执行时间，结果稳定性及精确度等方面都优于GA，DE，ACO，SA和TS。人群搜索算法(SOA)[13]，通过随机挑选一定数量的志愿者，基于一定的启发式信息、搜索规则和策略等，模拟人群搜索/觅食行为。目前该算法已用于函数优化、IIR数字滤波器设计、电力系统无功优化等领域[14]，与DE，APSO，CFPSO和CLPSO算法比较，SOA算法具有较好的全局寻优能力、较快的收敛速度和算法鲁棒性[15]。本文提出一种改进的自适应SOA算法(ISOA)，并将该算法应用于图像分割中，分割效果较满意。本文主要研究性能相对较好的SOA，PSO，GA和SA算法，同时也为了验证ISOA能用于多尺度图像分割。

1N尺度阈值分割模型

多尺度图像分割是一种有效的图像分割方法，而n尺度阈值寻优的鲁棒性对于图像分割则是一个难点。本节提供一种更精确的解决方法，下面介绍一些基本的表达式[9]。

给定一个最大灰度值L(本文直接设为256)，对于一副灰度图像而言，阈值取值为{0,1,2，…，L-1}，定义

其中i表示具体的灰度值，0≤i≤L-1，N表示图像的像素个数，hi表示i灰度值的个数，pi表示概率值，则灰度的平均值为：

二维阈值尺度问题能够拓展到n维阈值尺度，考虑n-1个不同阈值尺度tj，j=1,2,3,…,n-1，具体的表达式如下：

(1)

其中：x表示H×W图像的宽度坐标值；y表示H×W图像的高度坐标值，其像素二维函数为f(x,y)，待分割图像将被分成D1，D2，…，Dn类，组成F(x,y)。

最简单并且最快速的阈值寻优方法是，直接找出不同类之间最大方差对应的灰度值，一般定义如下：

(2)

其中：j代表一个具体的类；wj表示第j类的概率；μj为第j类的均值；具体的D1，D2，…，Dn类的wj和μj表示如下：

(3)

(4)

从而一个n尺度阈值问题降维为一个函数寻优问题，寻找阈值tj，使不同类间方差目标函数最大，目标函数如下：

(5)

相应的算法核心代码如下：

fitR(j)=sum(probR(1:xR(j,1)))*(sum((1:xR(j,1)).*probR(1:xR(j,1))/sum(probR(1:xR(j,1)))) - sum((1:Lmax).*probR(1:Lmax)) )^2;

forjlevel=2:level-1

fitR(j)=fitR(j)+sum(probR(xR(j,jlevel-1)+1:xR(j,jlevel)))*(sum((xR(j,jlevel-1)+1:xR(j,jlevel)).*probR(xR(j,jlevel-1)+1:xR(j,jlevel))/sum(probR(xR(j,jlevel-1)+1:xR(j,jlevel))))- sum((1:Lmax).*probR(1:Lmax)))^2;

end

fitR(j)=fitR(j)+sum(probR(xR(j,level-1)+1:Lmax))*(sum((xR(j,level-1)+1:Lmax).*probR(xR(j,level-1)+1:Lmax)/sum(probR(xR(j,level-1)+1:Lmax)))-sum((1:Lmax).*probR(1:Lmax)))^2;

fitBestR(j)=fitR(j);

%xR为种群个体，level为分割尺度，Lmax=256；

% probR为Pi概率值。

随着灰度级的增加，目标函数寻优将变得更复杂，计算量大大增加；因此，选取哪种算法进行优化模型分析，成为我们需要考虑的问题。

最近生物智能算法被广泛应用于目标优化分析，它是一种高效的智能算法。

2算法分析

随着智能算法的日新月异，算法的改进显得越来越重要，其计算速度、稳定性、全局寻优能力是当前研究的热点问题，改进的自适应人群搜索算法(ISOA)立足简化SOA算法[15]，通过对隶属度函数以及惯性权值的改进，简化了算法结构，缩短了算法执行时间，提高了算法稳定性以及全局寻优能力等。

2.1　搜索步长的确定

基本SOA算法，采用个体在当前种群中的相对位置排序，进行隶属度计算，增大了计算复杂度；而ISOA不确定推理行为的隶属度随迭代次数线性递增：

(6)

uij=ui+rand·(1-ui)，j=1,…,D

(7)

其中，ui为第i代个体对应目标函数值φ的隶属度，本文采用线性隶属函数，在最佳位置有最大隶属度值umax=1.0，最差位置有最小隶属度umin=0.011 1；iter和itermax分别为当前迭代次数和最大迭代次数；uij为j维搜索空间第i代个体对应目标函数值φ的隶属度；D为搜索空间维数。

由不确定推理可得步长：

(8)

其中，αij为j维搜索空间的搜索步长；δij为高斯隶属函数参数，计算如下：

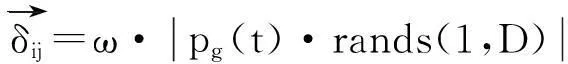
(9)

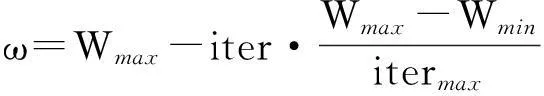
(10)

式中：pg(t)为种群全局最优值；rands(·)为[-1, 1]随机变量；ω是惯性权值，Wmin和Wmax分别为相应的最小最大权值。

2.2　搜索方向的确定

采用第i代个体的利己方向、利他方向以及预动方向随机加权平均，确定搜索方向如式(11)：

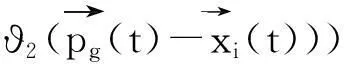
(11)

式中：pi(t)为种群个体最优值；xi(t-1)为上一代个体；sign(·)为符号函数；ϑ1和ϑ2为[0，1]随机数。

2.3　个体位置的更新

确定搜索方向和步长后，进行位置更新：

Δxij(t+1)=αij(t)dij(t)

(12)

xij(t+1)=xij(t)+Δxij(t+1)

(13)

相应的算法核心代码如下：

% maxgen=itermax,t=iter迭代次数

% 惯性权值,Wmax=0.9,Wmin=0.1

W=Wmax-t*(Wmax-Wmin)/maxgen;

% 隶属度值Umax=1.0,Umin=0.011 1

u=Umin+t*(Umax-Umin)/maxgen;

U=u+(1-u)*rand; % 隶属度

T= sqrt(-log(U)); % 搜索步长

% 确定利己方向，gbest为pi(t)

Diego(i,:) = (gbest(i,:) - pop(i,:));

% 确定利他方向，zbest为pg(t)

Dialt(i,:) = (zbest - pop(i,:));

% 确定预动方向，pop_1为上一代个体

Dipro(i,:) = (pop(i,:) - pop_1(i,:));

% 确定经验梯度方向

Di(i,:) = sign(W* Dipro(i,:) +rand*Diego(i,:) +rand*Dialt(i,:));

% 确定高斯函数的参数，N_PAR=D

C(i,:) =W*abs(zbest.*rands(1,N_PAR));

Bc(i,:) =C(i,:)*T;% 确定搜索步长

pop(i,:)=pop(i,:)+Di(i,:).*Bc(i,:); % 更新位置

3实验结果及分析

电脑配置为AMD A8-4500M(1.9 GHz)，2 GB可用内存，软件MATLAB(2014a)。图像大小均为200×400，图1为不同图像及其直方图。

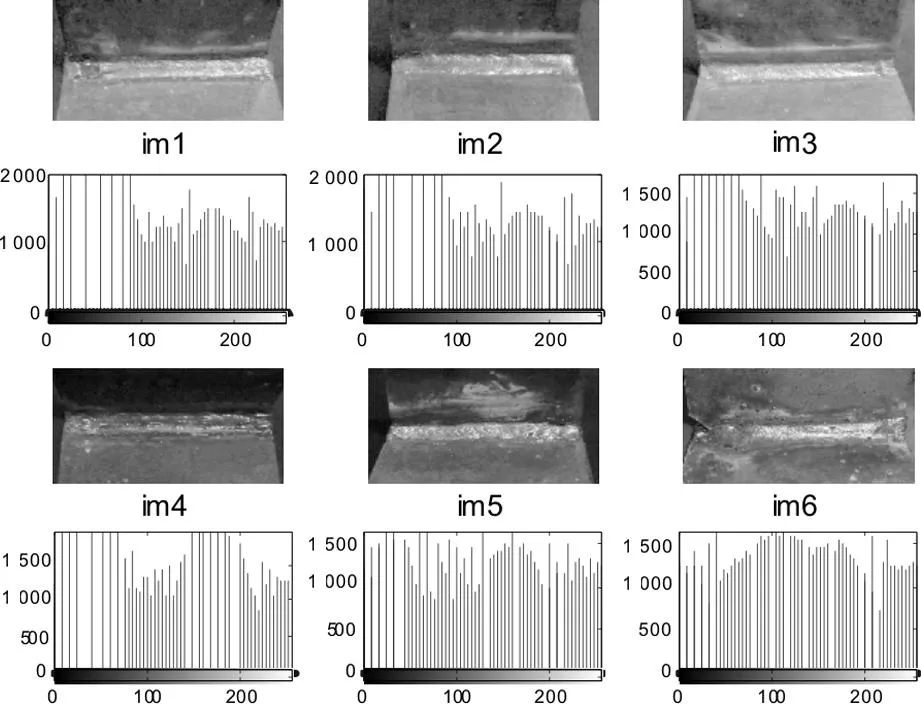
图1　不同的图形及对应的直方图Fig.1 Histogram of different image

初始化粒子速度均设定为0，粒子的位置在可行域内随机产生，搜索空间取决于图像灰度值的范围，也就是说如果图像是8位色图，那么粒子的寻值空间为0~255。ISOA，PSO，GA和SA都是参数化的算法，为了增强对比效果，选取迭代次数为50，种群数为30(等效于SA迭代次数(链长)为30)。其中，PSO算法粒子速度满足[vmin,vmax]=[-5, 5]，GA算法交叉概率为pc=0.8，变异概率为pm=0.2，SA初始温度T=1 000，降温速率q=0.5，本文中阈值尺度2≤n≤5，选取适应度估计值、CPU计算时间以及算法稳定性3个指标进行算法对比研究。

3.1　适应度值估计

因为算法是随机产生个体的，对于每一个尺度n，分别采用ISOA，PSO，GA和SA算法运行20次，统计各算法得到的适应度均值和标准偏差值，如表1所示。

如表1所示，阈值个数分别为2，3，4和5，尺度对应为3，4，5和6。尽管对于每一尺度，各算法计算的最优适应度值是相近的，然而随着阈值个数的增加，相对标准偏差值也增大。相比较，ISOA算法稳定且不易陷入局部最优。

表1　不同图像分割算法得到的适应度平均值±STD

3.2　CPU处理时间

衡量算法有效性的一个重要指标，就是CPU计算时间[9]，CPU计算时间越小，算法越能够被考虑来应用于实际控制器，算法执行时间过长，则算法本身有待改进。表2为不同算法的处理时间对比。

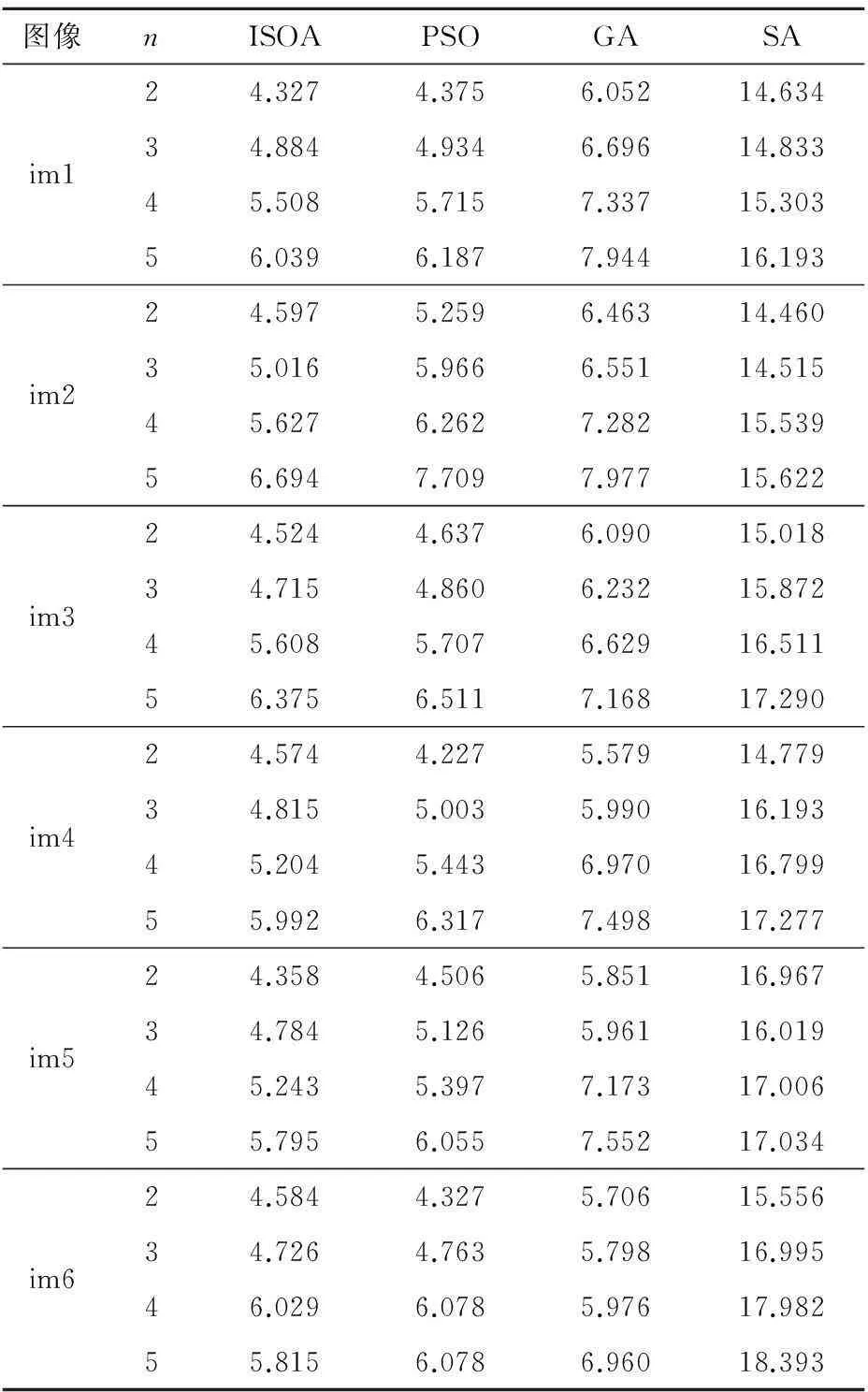
表2　不同图像分割算法的CPU处理时间

如表2所示，ISOA算法表现更好的性能，用时最短，其次是PSO，再次是GA，最后是SA算法。Hammouche等研究表明[12]，PSO图像分割是在CPU执行时间，结果稳定性、结果精确度等方面优于GA和SA。

为了直观的观察ISOA算法的分割结果，图2为不同尺度下的ISOA算法分割结果。

图2　图像分割结果(从左到右表示阈值个数为2，3，4，5)Fig.2 Image segmentation results(n=2,3,4,5 for image from left to right)

如图2所示，随着阈值个数增加，图像分割更加细致；当阈值个数为5时，即将图像分为6部分，图像显得更加平滑。

3.3　算法全局寻优分析

考虑到生物智能算法都具有随机性特点，即每一次运行结果是不完全相同的，因此有必要进行算法的全局寻优能力分析。

为了定义算法的全局寻优能力，本文采用标准偏差来衡量，如式(14)所示。

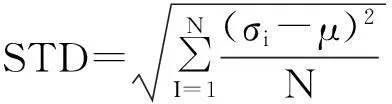
(14)

式中：STD是标准偏方差；σi是第i次算法运行得到的适应度值；μ是σ的平均值；N是算法执行的次数，在此取N=20。STD值越小，则表示算法的稳定性越强。阈值取值分别为2,3,4,5，针对每一个阈值，算法均运行N次，统计数据得如表1所示结果。

为了提高表1的可读性，图3表示采用不同算法，对不同尺度下的不同图像的适应度值标准偏差计算统计图。

如图3所示，GA是最不稳定的，ISOA是相对最稳定的，综合各项指标，ISOA是一种性能最佳的图像分割算法。

4结论

1)提出了一种ISOA算法的焊缝图像分割算法，ISOA算法通过改进高斯隶属函数以及自适应惯性权值，达到性能改进的目的，实验结果表明，该算法具有快速收敛、全局寻优能力等特点。

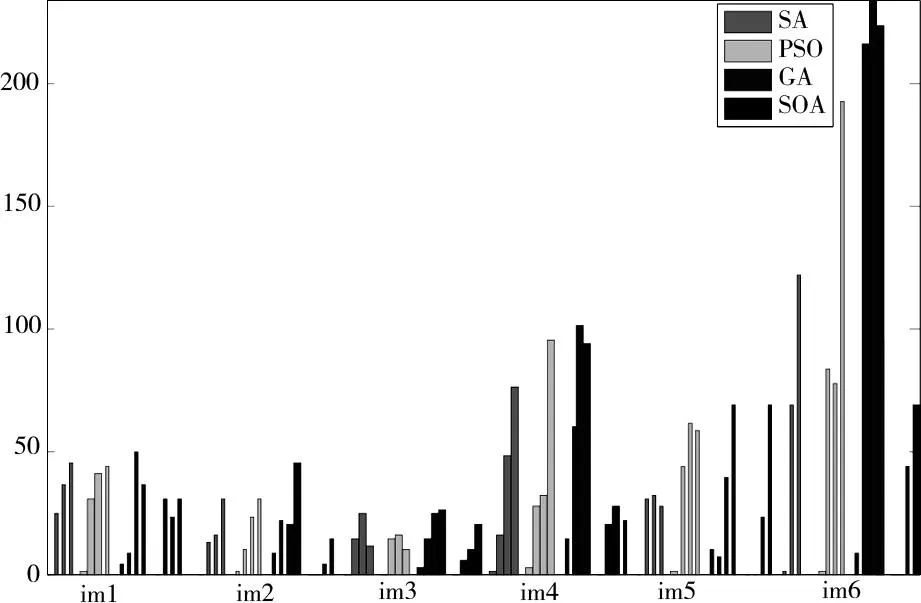
图3　不同的图像不同的STD值(从左到右表示2，3，4，5个阈值)Fig.3 STD values for image segmentation results(n=2,3,4,5 for image from left to right)

2)将ISOA算法成功应用于焊缝图像分割，实现了Otsu多级阈值下的焊缝图像分割，对比于PSO,Ga和SA算法，基于适应度值，STD和CPU计算时间性能指标，试验结果表明，采用ISOA算法性能更好，不易陷入局部最优，且随着阈值个数的增加，分割效果越好。

3)一方面，焊缝图像分割的自动化能够很好地实现焊缝的定位，且快速检测表面有明显缺陷的焊缝，另一方面，能够降低人工目测检测周期长，操作困难等缺陷。由于焊缝图像受外界干扰影响较大，就需要保证算法的适应性，ISOA算法根据用户设定的分类数，自动进行图像的阈值最大化分割，并且分割结果能够很好的自动识别焊缝，因此基于ISOA算法在T型焊缝图像分割的成功应用，具有广泛的应用前景，例如PID参数整定、遥感图像分割、视频分析等领域。

参考文献：

[1] 李娜，李元香.基于自适应粒子群算法和数据场的图像二维阈值分割[J]．计算机辅助设计与图形学学报,2014,24(5):628-635.

LI Na, LI Yuanxiang.Image segmentation with two-dimension threshold based on adaptive particle swarm optimization and data field[J]．Journal of Computer-Aided Design & Computer Graphics, 2014, 24(5):628-635.

[2] 余胜威,丁建明.转向架构架焊缝表面质量检测研究[J].铁道科学与工程学报,2015,12(2):402-406.

YU Shengwei, DING Jianming.Quality detection reaearch on bogie frame welding surface[J].Journal of Railway Science and Engineering, 2015,12 (2):402-406.

[3] 梁硼.X射线焊缝图像缺陷自动提取与识别技术研究[D].南京：南京航空航天大学,2012.

LIANG Peng.Research on technology of automatic extraction and identification for weld defects in X-Ray image[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2012.

[4] 余刚.钢制对接焊缝缺陷超声相控阵检测图像特征与识别[D].南昌：南昌航空大学,2012.

YU Gang.Defect image characterization and recognition of steel butt welds based on ultrasonic phased array[D].Nanchang：Nanchang Hangkong University, 2012.

[5] ZHANG Jing,JIN Yanxia.Genetic algorithm for weld image edge detection[J].IEEE,2010:511- 513.

[6] Xianghua Hou,Honghai Liu.Welding image edge detection and identification research based on canny operator[J].IEEE,2012:250-253.

[7] Brink A D.Minimum spatial entropy threshold selection[J].IEE Proceedings on Vision Image and Signal Processing, 1995, 142(3)：128-132.

[8] Kulkarni R V, Venayagamoorthy G K.Bio-inspired algorithms for autonomous deployment and localization of sensor nodes[J].IEEE Transactions, 2010, 40(6)：663-675.

[9] Pedram Ghamisi, Micael S Couceiro, Jón Atli Benediktsson, et al.An efficient method for segmentation of images based on fractional calculus and natural selection[J].Expert Systems with Applications, 2012, 39(16): 12407-12417.

[10] 胡卫东,曹文贵.基于粒子群BP网络混合算法的边坡稳定性评价[J].铁道科学与工程学报,2015,2(1):66-71.

HU Weidong, CAO Wengui.Slope stablitity evaluation based on hybrid algorithm of particle swarm optimization and BP neural network[J].Journal of Railway Science and Engineering, 2015,2(1):66-71.

[11] 邓连波,史峰,莫辉辉.物流配送车辆路径问题多代竞争遗传算法[J].铁道科学与工程学报,2015,2(5):75-79.

DENG Lianbo, SHI Feng, MO Huihui.Muilt-generation compete genetic algorithm for logistics distribution vehicle routing problem[J].Journal of Railway Science and Engineering, 2015,2(5):75-79.

[12] Hammouche K, Diaf M, Siarry P.A comparative study of various meta-heuristic techniques applied to the multilevel thresholding problem[J].Engineering Applications of Artificial Intelligence, 2010, 23(5)：676-688.

[13] 戴朝华,陈维荣,朱云芳,等.IIR数字滤波器设计的搜寻者优化算法[J].西南交通大学学报, 2009, 44(6): 871-876.

DAI ChaoHua, CHEN Weirong, ZHU Yunfang, et al.IIR digital filter design via seeker optimization algorithm[J].Journal of Southwest Jiaotong University, 2009, 44(6): 871-876.

[14] Dai Chaohua, Chen Weirong, Zhu Yunfang, et al.Reactive power dispatch considering voltage stability with seeker optimization algorithm[J].Electric Power System Research, 2009, 79(10): 1462-1471.

[15] 余胜威,曹中清.基于人群搜索算法的PID控制器参数优化[J].计算机仿真,2014,31(9): 347-350.

YU Shengwei, CAO Zhongqing.Optimization parameters of PID controller paraters based on seeker optimization algorithm[J].Computer Simulation，2014,31(9): 347-350.

(编辑阳丽霞)

Improved seeker optimization algorithm application in weld image segmentation

YU Shengwei1, DING Jianming2, CAO Zhongqing1

(1.College of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China;

2.State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)

Abstract：This paper present's a new novel method which is called improved seeker optimization algorithm .Gaussian membership function and its parameters of traditional SOA algorithm are optimized, and the step length is determined by uncertainty reasoning based on adaptive principle.Besides, improved SOA is able to decide the n-1 optimal for n-level threshold on a given image.Compared with PSO, GA and SA algorithm, testing results show that improved SOA enhances the performance in terms of convergence speed, stability, solution accuracy and global optimality.ISOA could also greatly overcome the shortcomings of traditional methods, such as local optima and slow convergence speed.Hence, improved SOA can be widely employed in practical engineering.

Key words：multi-scale segmentation; ISOA; class variance; PSO; GA; SA

通讯作者：丁建明(1981-)，男，四川巴中人，博士，从事机械设计、故障诊断研究；E-mail:fdingjianming@126.com

基金项目：国家自然科学基金重点资助项目(61134002)

收稿日期：2015-06-11

中图分类号：TP391.4

文献标志码：A

文章编号：1672-7029(2015)06-1471-07