考虑波长因素的轨道不平顺预测研究

吕宏 ,李再帏,2,3, 何越磊

(1.上海工程技术大学 城市轨道交通学院, 上海 201620；

2.华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013；

3.北京交通大学 土木建筑工程学院, 北京100044)



考虑波长因素的轨道不平顺预测研究

吕宏1,李再帏1,2,3, 何越磊1

(1.上海工程技术大学 城市轨道交通学院, 上海 201620；

2.华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013；

3.北京交通大学 土木建筑工程学院, 北京100044)

摘要:准确预测轨道不平顺的变化规律是提高轨道养护维修效率、降低维修成本的关键问题之一。鉴于轨道不平顺波长对列车运行状态的影响，基于小波理论，通过选取合适的小波基函数及分解层数，对原始不平顺时域序列进行小波分解及重构，并采用不平顺状态推移方法对重构后不平顺序列进行分析处理，利用不同时刻下轨道不平顺的状态分布，从而实现对轨道不平顺预测；通过2个实际算例对本方法正确性进行验证，并对预测结果进行误差分析。研究结果表明：利用本文提出方法得出的预测结果与实际结果误差较小，可以有效地预测轨道不平顺的变化趋势，且能够实现不同波长段轨道不平顺的预测，可为我国轨道养护维修方案的制定提供一定的技术支持。

关键词：小波理论；轨道不平顺；预测方法；状态推移法

轨道不平顺是轨道结构形变的外部综合反映，是产生车辆系统振动的主要根源，同时也是轨道系统动力分析与轨道养护维修及质量评估中的重要基础资料，其对轮轨系统动力传播、轮轨噪声和线路养护维修等方面的研究都有十分重要的作用。由于不同波长的轨道不平顺对于轨道线路的影响不尽相同，对于高速铁路而言，在列车高速运行区段，其长波不平顺对列车运行状态影响较为明显，而在列车低速运行区段，其局部的短波不平顺影响较为严重，易多激扰起较大轮轨力，对列车运行安全产生较大影响。因此，利用现有检测数据实现不同波长区段轨道不平顺的预测具有十分重要的意义。影响轨道不平顺变化的因素较多，各因素的影响程度也各不相同，且由于环境、路基状态等部分因素难以具体描述。因此，国内外学者针对轨道不平顺变化问题展开了大量研究：日本学者[1-3]先后通过多参数分析法、回归分析法、指数平滑法和频域分析法等方法，利用轨检车数据及轨道基本参数从幅值角度对不平顺预测模型进行了探索；我国在轨道不平顺预测方面也取得了部分研究成果：许玉德等[4]利用线性预测模型，对铁路轨道质量指数(TQI)的发展进行了预测研究；陈宪麦等[5]提出了一种用于轨道不平顺发展预测的综合因子法，对轨道不平顺发展趋势进行预测；曲建军等[6]提出利用灰色预测模型，实现了对轨道TQI指数变化趋势的预测。高建敏等[7]提出了一种基于不平顺分布函数的不平顺发展统计预测方法，实现轨道不平顺的预测。上述方法均能有效地预测出轨道不平顺的变化趋势，对铁路线路养护维修周期制定起到了积极作用，但值得注意的是，这些研究多是局限于轨道不平顺幅值角度进行预测，并未涉及到不同波长轨道不平顺的变化趋势。而随着高速铁路及城市轨道交通的不断发展，不同里程段上轨道不平顺呈现出的波长分布特性存在一定的差异。同时，对于不同里程段上所关注的轨道不平顺波长范围也不尽相同。因此，需要一种可以实现不同波长特征的轨道不平顺预测的方法。鉴于小波分解理论具有多频段分析和适应性分析的特点[8]，且在不平顺局部波型辨识、轨道病害识别等方面都有一定地应用[9]。本文在已有的研究基础上，引入小波理论，进而提出一种考虑波长因素的轨道不平顺预测方法，从而为我国铁路养护维修及工务部门的精细化和高效管理方面提供相应技术支撑。

1基本原理

1.1　小波分解及重构原理

对于函数x(t)∈L2(R)，L2(R)表示一个平方可积的实数空间，x(t)的离散小波变换定义为：

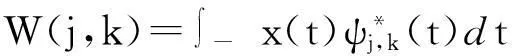
(1)

ψj,k=α-j/2Ψ(α-jn-kβ)

(2)

其中：α和β为标度因子。令α=2,β=1，则式(2)表示二进正交小波基函数，再通过此式对x(t)进行小波分解，即可得相应小波系数：

W(j,k)={U,di,di-1,…,d1}

(3)

其中：U为低频小波系数；i为小波分解层数；di为第i层高频小波系数。对离散小波的逆变换重构定义为：

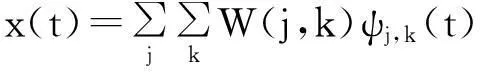
(4)

1.2　轨道不平顺状态推移模型

基于轨道不平顺随时间变化特性及不同时刻下轨道不平顺的概率分布，这里采用一种状态推移的模型来对轨道不平顺变化进行描述，模型建立基本流程为：根据不平顺数据的范围，将轨道不平顺划分为n个离散区间，这些区间可视为轨道不平顺的不同状态，则属于这些状态的检测点的数量为S1,S2,···,Sm；再计算由某时刻η-1到时刻η的各状态转换的概率，记为Pab，则有以下表达式：

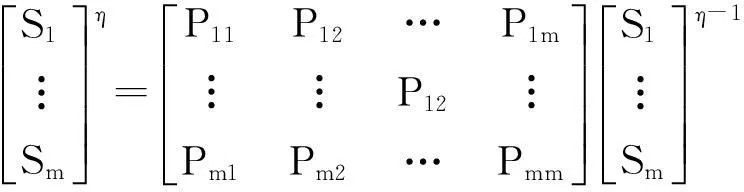
(5)

当事件状态的概率分布未知时，若样本的容量较大，则可以通过对样本计算近似地描述理论的状态概率分布。本文利用实测的轨道不平顺数据，选取不同时刻下固定线路里程中的测量点作为样本。通过对计算样本的推移频率近似得到理论的推移概率。其计算公式为：

Pab=aab/ab(a,b=1,2,…,m)

(6)

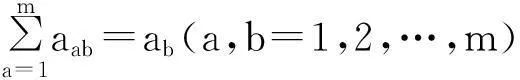
2基于小波分解的轨道不平顺预测方法

本文在状态推移预测模型基础上，引入小波分解理论，通过对原始轨道不平顺时域序列进行小波分解及重构，得到新的不平顺时域序列，并对其应用状态推移预测模型，从而实现不同波长的不平顺预测功能。其具体步骤如下：

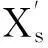
流程图如图1所示。

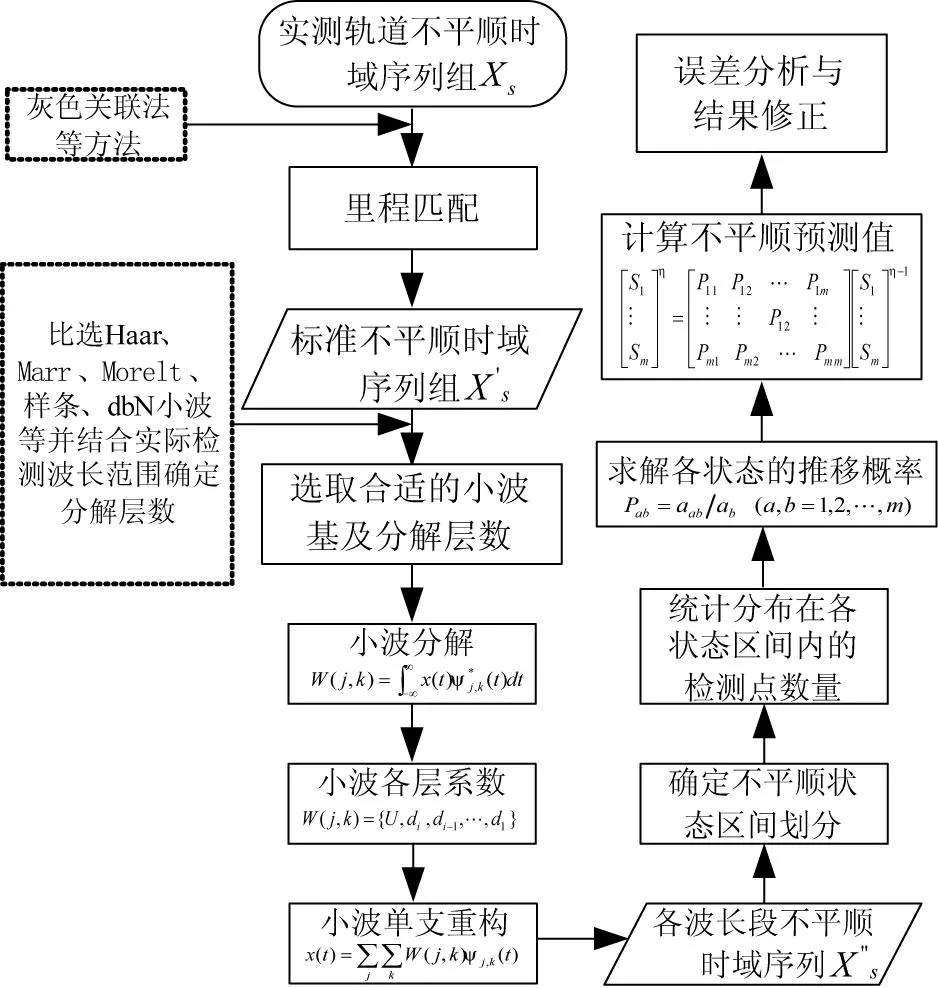
图1　预测方法流程图Fig.1 Flow chart of theprediction method

3算例验证

为验证上述方法的正确性，本文通过选取2个算例，利用2013年合武线及2011年京广线轨检车实测数据，对轨道不平顺状态的变化规律进行研究与分析。

3.1　算例1

3.1.1数据选择

根据轨检车实测数据的保存形式，本文选取了连续3次同一位置的合武线上行2 km里程范围内的实测数据。需说明的是：所选里程段均为有砟轨道，设计时速为250 km/h，测试车辆为0号综合轨检车，采样间隔为0.25 m。且通过计算可知所选取的样本均值，方差与据检车全段检测数据的均值，方差大致相等，因此说明本文所选取的样本容量具有代表性，可以表征线路整体不平顺的分布情况。同时，由于预测效果与线路维修息息相关，因此本文通过查阅相关维修记录，从而确保所选的3次检测时间范围内进行的维修作业量为最少。此外，由于轨检车检测对象包括轨距、左高低、右高低、左轨向、右轨向、水平和三角坑等，对于不同的检测对象，它们对轨道质量的影响程度也不尽相同。因此针对不同种类的轨道不平顺，本文提出的预测方法在检测不平顺状态区间划分及检测周期的选取上都不尽相同。限于篇幅本文仅以高低不平顺为例，选择实测的左高低数据作为样本数据。

3.1.2小波基与分解层数选取

本文选取具有紧支集及较好正则性的Daubechies小波(dbN)作为小波基函数。Daubechies小波(dbN)系列随着序号N的增加，小波基函数频带划分效果和时域波形的光滑性越好，表现出较好的局域性能。但同时会使时域紧支撑性减弱，同时计算量增加，实时性变差，因此综合考虑本文选取db6小波作为小波基函数[10]。

由于轨检车的采样间隔为0.25 m，且由于轨检车检测波长的范围为1.5~120 m，而小波分解后第i层对应波长区间大致为[λs·2i,λs·2i+1](λs为采样间隔)，因此当选取小波分解层数为8时，最后一层的波长区间为64, 128 m，已满足所需波长范围的要求，因此本文选用小波分解的层数为8层。

3.1.3预测结果分析

本文选取前两个时刻下的高低不平顺序数据为参考序列，通过本文提出的方法对下一时刻下的高低不平顺序进行预测，并将预测结果与实测数据进行对比。为减小不同时刻下检测数据存在的里程偏差，本文采用灰色关联法进行里程匹配[11]。通过计算分别将前两次的检测数据平移55.25和59.5 m作为标准里程。得到新不平顺时域序列后，再对3组高低不平顺序列进行小波分解及重构，选取上述小波基及分解层数，限于篇幅，图2仅为第1次检测数据小波重构后的轨道不平顺预测序列。

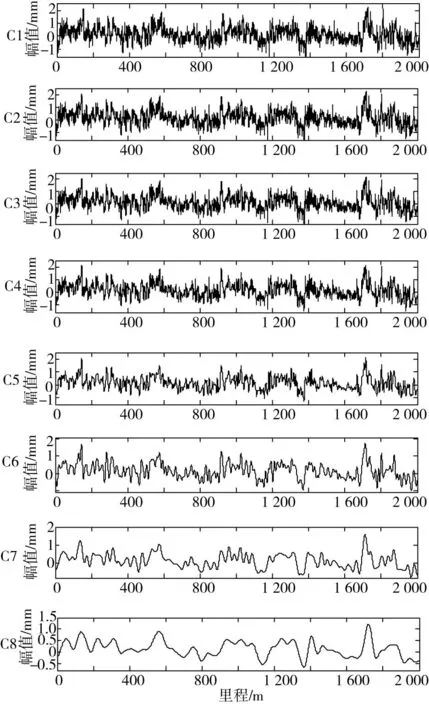
图2　各波长段小波重构后的不平顺序列Fig.2 Wavelet reconstructed irregularity of different wavelength

在得到重构不平顺序列的基础上，根据实测数据的极差，进行高低不平顺的状态划分，由于状态区间个数的确定与线路实际养护维修具体要求有关，通常情况下区间个数越小，即区间长度越大，则频数分布较为集中，预测效果越好。而在实际运用中由于不同里程及波长段的不平顺要求不尽相同，因此状态区间的划分需按线路的实际要求来确定，从而满足现场实际需求。所以，在满足现场预测精度的前提下，应尽可能地多划分状态区间，从而达到更加精确地预测效果；通过前期大量的试算和分析，并结合相关文献[7]的研究结果，这里选取了15个状态，即划分16个区间。此外，由于不同波长段小波重构后轨道不平顺的幅值有所变化，所以需确保3组不平顺序列进行小波重构后对应波长段的区间划分一致。

状态区间划分后，即可通过状态推移法计算各区间频数的推移概率Pab，具体方法如下：设3组不平顺序列分别对应时刻1，2和3所采用的轨检车检测数据，先统计每一次不平顺检测数据各区间段检测点频数ab(b=1,2,…,15)，再统计时刻1检测数据某一区间段检测点频数ab变化到时刻2各区间的频数aab(a,b=1,2,…,15)，即表示原来满足时刻1下的某一状态区间的检测点由于轨道恶化从而不平顺值发生了变化，导致这些检测点在时刻2划分区间时被统计到了其他各个区间。统计完区间频数ab以及区间变化频数aab后，即可通过式(6)计算出相邻两时刻下不平顺区间频数的推移概率Pab。最后即可在时刻2检测数据的基础上，由式(5)预测出时刻3的不平顺区间频数分布。第3次不平顺检测数据各波长段的预测结果与实际结果的对比如图3所示：

由图3可知，利用本文所提方法得出的预测值与轨检车的实际值之间较为符合。对于预测结果和实际值之间存在部分偏差，可能是由于线路的不断维修，导致在部分位置上的检测数据发生较大变化，从而产生误差。

3.1.4误差分析

为验证本文所提方法准确性，这里采用传统的状态推移法与本文方法进行对比。通过计算预测值和实际值之间的相关系数，分析2种方法预测结果的精度，从而确定方法准确性，计算结果如表1所示。

表1　预测方法评价指标

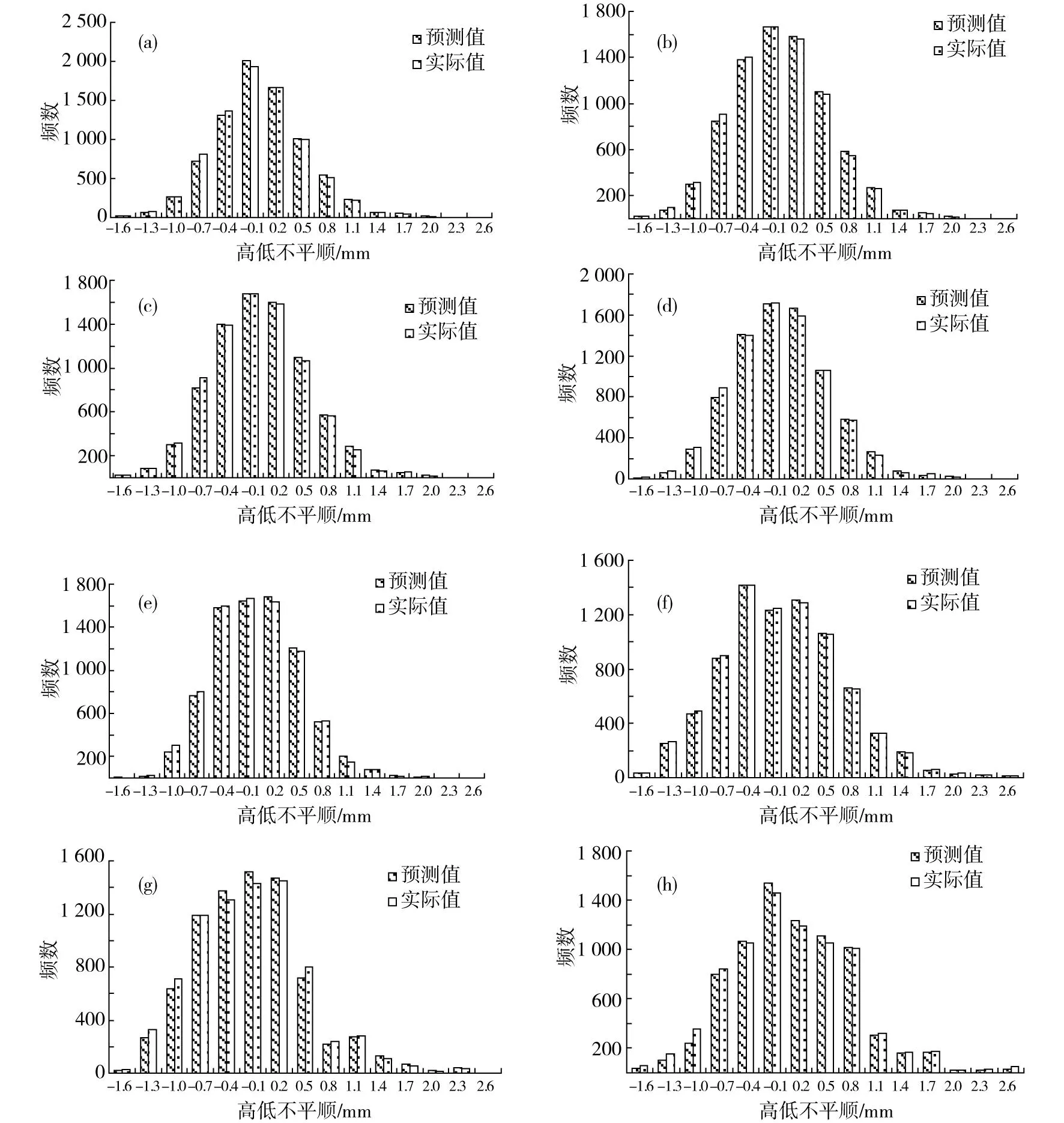
(a)波长0.5~1 m;(b)波长1~2 m;(c)波长2~4 m;(d)波长4~8 m;(e)波长8~16 m;(f)波长16~32 m;(g)波长32~64 m;(h)波长64~128 m图3　高速铁路第3次检测数据各波长段预测值与实际值分布对比Fig.3 Contrast between the third detection data’s predicted value and actual value of different wavelength in high-speed railway

由表1可得，本文方法预测值与实际值拟合情况较好，且与其他方法相比，其相关系数大致相等，说明本文方法与其他方法的预测精度相近，可以满足实际养护维修工作预测精度要求。

3.2　算例2

数据来源为京广既有提速线上行有砟轨道线路，3次同一里程区间检测数据，长度为2 km，轨检车类型及相关参数与算例一相同，同样针对轨道高低不平顺进行分析。通过计算分别将前两次的检测数据平移62.5和67.75 m作为标准里程。则通过上述方法得到的第3次不平顺检测数据各波长段的预测结果与实际结果的对比如图4所示。

由图4可知，利用本文所提方法得出的预测值与轨检车的实际值之间较为符合。通过计算各波长段预测值与实际值之间的相关系数，得到方法的预测精度，计算结果与算例一相近。结果表明本文所提方法可以满足实际养护维修工作预测精度要求。

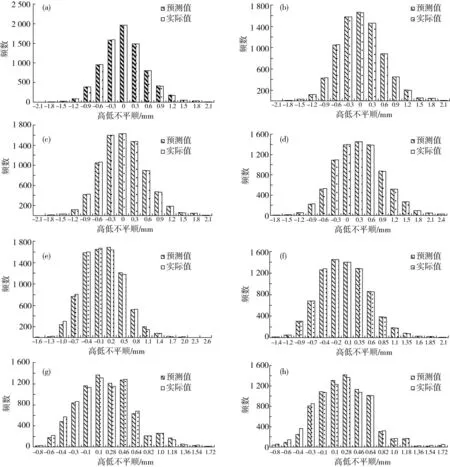
(a)波长0.5~1 m;(b)波长1~2 m;(c)波长2~4 m;(d)波长4~8 m;(e)波长8~16 m;(f)波长16~32 m;(g)波长32~64 m;(h)波长64~128 m图4　既有线第3次检测数据各波长段预测值与实际值分布对比Fig.4 Contrast between the third detection data’s predicted value and actual value of different wavelength in existing speed line

综上所述，本文通过对2种不同运行速度下的轨道不平顺检测数据进行方法的验证和分析，其预测结果与实际值较为符合。因此，说明本文提出的方法可以正确预测不平顺的变化趋势，且与其他方法相比，本文方法还可以实现不同波长段轨道不平顺的预测。

4结论

1)利用小波分解的预测方法，可以实现轨道不平顺有效预测；且与现有的轨道不平顺预测方法相比，可以实现不同波长段的轨道不平顺预测。

2)预测所需要的原始数据可通过轨检车数据处理后直接得到，数据源容易获取，使得该方法简单且实用。

3)该方法可以通过各状态的变化推移计算出轨道不平顺由某一范围变化到另一范围的数量及概率，可以反映出在不同时刻下轨道整体质量的变化趋势，在评估轨道质量，制定养护维修计划等方面都有一定应用价值。

4)由于线路的不断维修，在部分位置上的检测数据可能发生较大变化，因此还需进一步完善该方法，对其进行相关处理，进而实现更为精准的预测。

参考文献：

[1] 佐藤吉彦.日本高速铁路的全寿命维护[J].中国铁道科学， 2001, 22(1): 6-14.

Misaki Sato Yoshihiko.The life cycle ma-intenance of high speed railways [J].China Railway Science， 2001, 22 (1): 6-14.

[2] Hideo Miyamoto.日本东海道新干线三十年轨道维修经验[J].上海铁道科技， 1998(2):43-45.

Hideo Miyamoto.The thirty years of trackmaintenance experience of Japanese Tokai-do Shinkansen[J].Shanghai Railway Science & Technology， 1998(2): 43-45.

[3] 内田雅夫.高速铁路轨道的维修管理[J].铁道建筑， 1992(10): 6-9.

Uchida Masao.The high speed railway track repair management[J].Railway Engineering， 1992(10): 6-9.

[4] 许玉德, 吴纪才.利用线性预测模型分析轨道不平顺发展[J].石家庄铁道学院学报, 2005, 18(1): 6-9.

XU Yude, WU Jicai.Analysis on development of track irregularities with linear forecast Model[J].Journal of Shijiazhuang Railway Institute, 2005, 18 (1): 6-9.

[5] 陈宪麦.轨道不平顺时频域分析及预测方法的研究[D].北京：铁道科学研究院, 2006: 99-101.

CHEN Xianmai.Time frequence analysis and prediction study on track irregularities[D].Beijing: Chinese Railway Science Research Institute, 2006: 99-101.

[6] 曲建军, 高亮, 张新奎, 等.基于灰色GM(1,1)非等时距修正模型的轨道质量预测[J].中国铁道科学, 2009, 30(3): 5-8.

QU Jianjun, GAO Liang, ZHANG Xinkui,et al.A prediction method for track quality based on grey GM(1,1) nonequal time interval correction model[J].China Railway Science.2009, 30(3): 5-8.

[7] 高建敏.基于状态转移概率矩阵的轨道不平顺发展预测研究[J].铁路建筑, 2011(7): 140-143.

GAO Jianmin.The development of the track irregularity prediction research based on The state transition probability matrix[J].Railway Engineering, 2011(7): 140-143.

[8] 陈宪麦, 王澜, 陶夏新, 等.基于小波分析理论的轨道不平顺分析[J].铁道工程学报, 2008, 1(1): 57-61.

CHEN Xianmai, WANG Lian,TAO Xiaxin,et al.The analysis of track irregularity based on the theory of wavelet analysis[J].Journal of Railway Engineering Society, 2008, 1(1): 57-61.

[9] 徐磊, 陈宪麦, 徐伟昌, 等.基于小波和Wigner-Ville分布的轨道不平顺特征识别[J].中南大学学报(自然科学版), 2013, 44(8): 3344-3350.

XU Lei, CHEN Xianmai, XU Weichang,et al.Explored of track irregularity’s characteristic identification based on wavelet method and WignerVille distribution[J].Journalof Central South University(Science and Technology), 2013, 44(8): 3344-3350.

[10] 曲铭, 许玉德.基于小波的列车加速度和轨道不平顺关系分析[J].华东交通大学学报, 2008(5): 36-41.

QU Ming, XU Yude.An analysis of the relationship of acceleration and track irregularity based on wavelet[J].Journal of East China Jiaotong University, 2008(5): 36-41.

[11] 李再帏, 练松良.改进HHT方法在轨道不平顺信号分析中的应用[J].深圳大学学报(理工版), 2012, 29(3): 270-275.

LI Zaiwei， LIAN Songliang.Analysisof track irregularity signal by improved Hilbert Huang Transform[J].Journal of Shenzhen University Science and Engineering, 2012, 29(3): 270-275.

(编辑蒋学东)

Theprediction method considering the factors of track irregularity wavelength

LÜ Hong1,LI Zaiwei1,2,3, HE Yuelei1

(1.School of Urban Rail Transportation, Shanghai University of Engineering Science, Shanghai 201620, China；

2.Engineering Research Center of Railway Environmental Vibration and Noise of Ministry

of Education, East China Jiaotong University， Nanchang 330013, China;

3.School of Civil Engineering and Architecture, Beijing Jiaotong University, Beijing 100044, China)

Abstract:The accurate prediction of the change law of track irregularity is one of the key problems to improve the efficiency of track maintenance and reduce maintenance cost.According to the change trend of the track irregularity of different wavelengths and the influence on operation, and basing on the theory of wavelet decomposition, this paper selected the appropriate wavelet basis function and decomposition levels to complete the wavelet decomposition and its reconstruction for the original irregularity time domain sequence.By using the state shifting method to analyze the irregularity sequence after reconstruction, and making use of the different times of orbit the irregularity of the state distribution, the track irregularity was predicted.The feasibility of this mothod was verified by a practical example and the error between the outual results and the prediction results was analyzed.The results show that the error between the predicted results and the actual results using the method proposed in this paper is small.It can effectively predict the change tendency of track irregularity, and this method can realize the prediction of track irregularity of different wavelengths.The method can provide technical support for the research of track irregularity prediction in our country.

Key words：wavelet theory; track irregularity; prediction method; state shifting method

通讯作者：李再帏(1983-)，男，吉林大安人，副教授，博士，从事轨道结构振动研究；E-mail:lzw5220964@163.com

基金项目：上海市科学技术委员会地方院校能力建设资助项目(14110501300)；上海市研究生教育创新计划学位点引导布局与建设培育资助项目(13sc002)；上海市教育委员会科研创新资助项目(14YZ137)；上海工程技术大学研究生科研创新资助项目(14KY1005)

收稿日期：2015-04-09

中图分类号：U216

文献标志码：A

文章编号：1672-7029(2015)06-1312-07