一种拟合三维空间直线的新方法

许辉熙,薛万蓉2,程　熙3

(1. 四川建筑职业技术学院测量工程研究所, 四川 德阳 618000; 2. 四川建筑职业技术学院

测绘工程系, 四川 德阳 618000; 3. 成都理工大学,四川 成都 610059)

XUHuixi,XUEWanrong,CHENGXi

一种拟合三维空间直线的新方法

许辉熙1,2,3,薛万蓉2,程熙3

(1. 四川建筑职业技术学院测量工程研究所, 四川 德阳 618000; 2. 四川建筑职业技术学院

测绘工程系, 四川 德阳 618000; 3. 成都理工大学,四川 成都 610059)

ANewFittingMethodofThree-dimensionalSpatialStraightLines

XUHuixi,XUEWanrong,CHENGXi

摘要：提出了一种基于稳健总体最小二乘的三维空间直线拟合新方法。该方法以加权总体最小二乘为基础，通过删除点到拟合直线距离过大的观测点来抵抗粗差的影响，获得空间直线参数的稳健估计值。试验表明，当观测数据中不含有误差时，加权最小二乘法、加权总体最小二乘法和本文方法的参数估计值高度一致；当观测数据包含粗差时，本方法的参数估计值明显更接近真实值。

引文格式： 许辉熙,薛万蓉,程熙. 一种拟合三维空间直线的新方法[J].测绘通报，2015(9)：28-31.DOI:10.13474/j.cnki.11-2246.2015.0271

关键词：稳健估计;加权总体最小二乘;三维空间直线拟合

中图分类号：P258

文献标识码：B

文章编号：0494-0911(2015)09-0028-04

收稿日期：2015-03-30

基金项目：国家自然科学基金(41301488)；四川省教育厅自然科学项目(15ZB0448;15ZB0452)

作者简介：许辉熙(1979—),男,博士,副教授,主要从事地理学、空间信息技术应用研究。E-mail：529382949@qq.com

一、引言

三维空间直线拟合是工程测量和工业测量等工程应用领域的常见问题。三维空间直线可以用点向式表达为

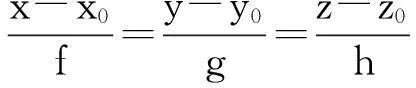
(1)

式中，(x0,y0,z0)为空间直线通过的已知点；(f,g,h)为空间直线的方向矢量。拟合平面直线是典型的线性问题，而拟合空间直线是一个明显的非线性问题，不能简单直接地借用拟合平面直线的加权最小二乘法(leastsquares，LS)和加权总体最小二乘法[1](weightedtotalleastsquares，WTLS)。

要运用LS法进行空间直线拟合，需要先将空间直线描绘成两个空间平面的交线形式,或将其垂直投影到坐标平面上，然后拟合平面或平面直线，最后重建空间直线[2-3]。也可以先拟合通过该空间直线的任何一个平面，然后在该平面上拟合平面直线，最后将平面直线还原为空间直线[4]。很显然，这些方法含有某一个坐标分量不含误差的假设，不符合实际情况。文献[1]为消除上述假设，采用总体最小二乘法(totalleastsquares，TLS)进行空间直线拟合，取得了良好效果，但未针对含有粗差的情况进行讨论。三维空间直线拟合问题是一个非线性问题，因此可以采用非线性最小二乘法(nonlinearleastsquares,NLS)。文献[5]提出采用高斯-牛顿迭代算法拟合空间直线，这些迭代算法对初值有一定的要求，并且可能出现发散，从而得不到正确的参数估计结果。文献[6]讨论了稳健总体最小二乘法(robusttotalleastsquares,RTLS)在三维相似坐标变换中的应用。

目前，关于用RTLS法进行空间直线拟合的讨论并不多见。本文提出采用非线性拉格朗日函数法推导基于WTLS的一种择优录取RTLS算法。算法首先以含有粗差的观测数据拟合直线，然后计算各观测点到直线的距离，择优录取距离较小的点重新拟合空间直线。

二、总体最小二乘拟合三维空间直线

将式(1)进行简单变形，表达成如下的两个空间平面[1]

(2)

式中，ξ1=f/h;ξ2=x0-(fz0)/h；ξ3=g/h；ξ4=y0-(gz0)/h。因此，只要拟合出平面的4个参数就可以重建六参数形式的空间直线对称方程。假设有t(t>2)个实测空间点数据，用这些观测点拟合平面参数的矩阵形式为

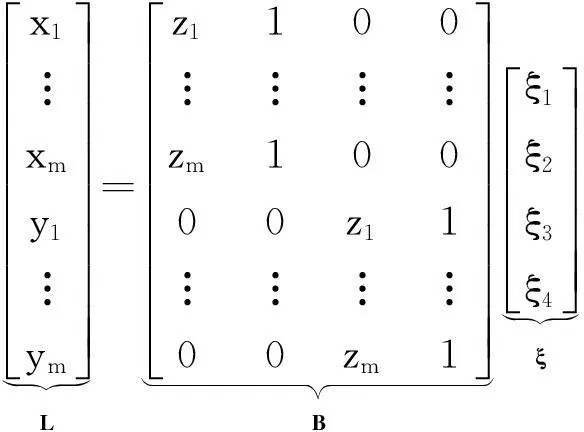
(3)

根据式(3)可以得到WTLS拟合空间直线的函数模型，即

L-eL=(B-EB)ξ

(4)

式中，eL和EB分别为观测值的随机误差矢量和矩阵，大小分别为m×1和m×4(m=2t)。从式(4)中可以明显发现，此时系数矩阵具有很强的结构特性。如果采用SVD分解解算将会使得系数矩阵中的常数变量分配到不应有的误差改正值，不同位置的同一变量得不到相同的改正值，这与理论不符，因此解算理论不严密。为了解决这种结构性问题，将式(4)进行改写，使误差矩阵只与z坐标分量误差有关，即

L-eL=Bξ-(ξT⊗Im)Hez

(5)

式中，Hez=eB=vec(EB)。H为常数矩阵，vec()表示矩阵拉直计算，从左往右，将后一列加到前一列的后面。方程中的误差满足如下的随机属性

(6)

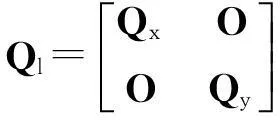
(7)

式中，Qx=Qy=Qz=Q，Q表示观测点之间的协因数矩阵。根据式(3)—式(7)的描述，可以得到如下的非线性拉格朗日函数

Φ=eLPleL+ezPzez+

2λT(L-eL-Bξ+(ξT⊗Im)Hez)

(8)

要使上述非线性拉格朗日函数的极小值存在，则Φ关于eL、ez、λ和ξ的偏导数等于零，即

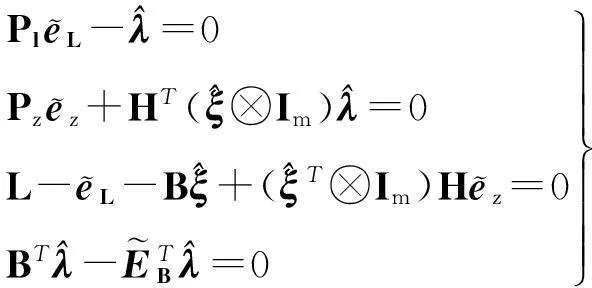
(9)

对式(9)进行推算整理，可以得到如下的参数估计公式

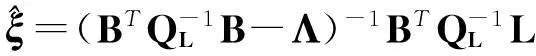
(10)

式中

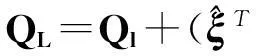
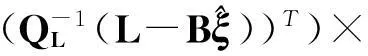
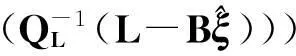
并且可以得到误差改正项的计算公式，即

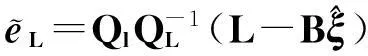
(11)

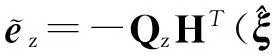
(12)

根据式(3)和式(11)可以得到x和y坐标分量的误差改正值，即

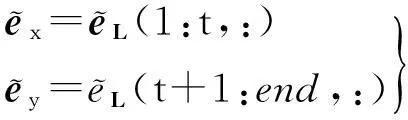
(13)

很显然，误差改正量等于观测点到拟合直线各坐标分量上的距离值。因此，点到直线的距离即是各坐标分量改正值的平方和的根，即

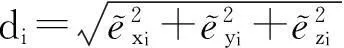
(14)

如此则可以根据点的观测精度确定极限距离，将式(14)确定的距离与极限距离相比，找出在极限距离范围内的点。最后的加权单位权方差估计值计算公式为

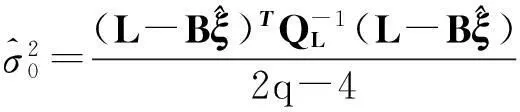
(15)

式中，q表示择优录取点的总数量。WTLS问题是一个简单的非线性问题，单位权方差估计值一般是有偏的。

三、稳健总体最小二乘拟合算法

随着三维激光扫描仪、激光跟踪仪及其他先进仪器在工程测量中的广泛使用，空间直线点云数据的获取成为可能。在点的采集过程中由于受到外界环境的影响，点云中可能包含有异常点。在利用WTLS法进行空间直线的参数拟合时没有考虑这些异常点的影响，拟合的空间直线参数与目标空间直线参数间存在较大差异。而RTLS法可以消除这些异常点，使得拟合的空间直线更接近目标空间直线。其具体计算流程如下：

1) 根据给定的坐标观测值和精度确定平差需要的观测矢量、系数矩阵及协方差因子。

2) 假设EB=0，采用LS法计算参数的初始值。

3) 采用式(10)循环计算参数的估计值直至相邻两次估计值之差的2范数小于指定限差，本文的限差设置为1Ε-10。

4) 采用式(11)—式(12)计算残差矢量，并将残差矢量描述成各坐标分量的残差矢量。

5) 采用式(14)计算观测点到拟合直线的距离。

6) 采用式(15)计算加权单位权方差估计值。

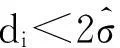
8) 利用择优录取的点重复步骤1)—步骤7)；直至相邻两次录取的点相同。

9) 输出估计的4个参数，将参数代入式(2)中恢复出空间直线的对称方程。

四、试验分析

在一条已知的空间直线

(16)

上随机产生200个空间点，如图1所示。将该空间

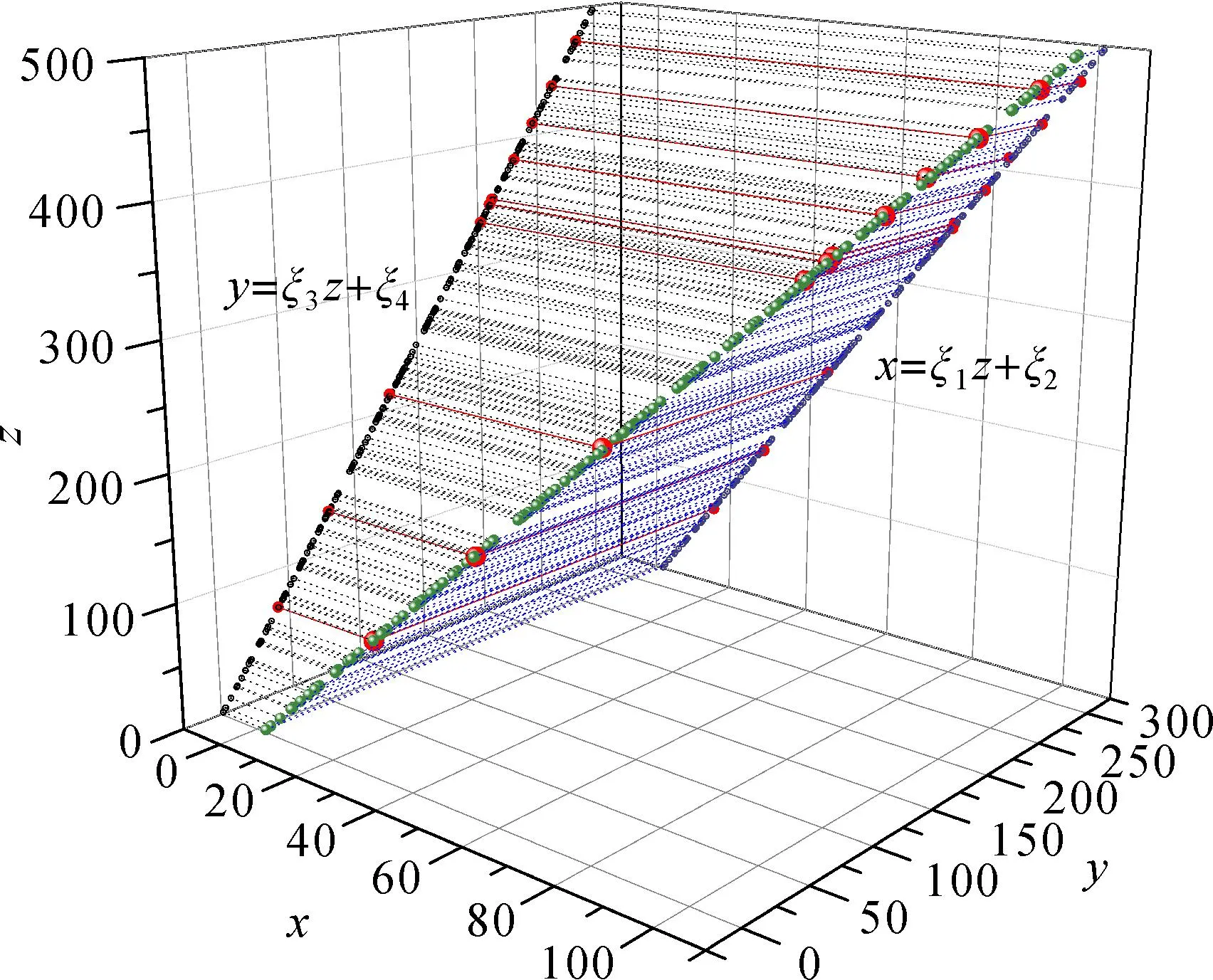
图1　原始模拟数据

直线投影到xoz和yoz坐标平面上，空间直线可以通过这两个垂直投影面表达，即

(17)

为了验证本文方法的可行性，设计如下两个试验方案。

1) 方案1：在不含有人为粗差的原始模拟数据中，对x、y、z坐标分量附加上期望为零、中误差为0.03的随机误差，产生一组模拟观测值；分别采用LS、WTLS和RTLS法估计式(2)的参数。

2) 方案2：在原始模拟数据中随机抽出10个点，在这些点上加上人为粗差，同样给这些粗差点和其余原始模拟点附加上期望为零、中误差为0.03的随机误差，并采用上述3种方法估计模型参数。

对方案1和方案2计算1000次，表1和表2分别列出了方案1和方案2的参数估计平均值和方差估计平均值。图2分别表达了方案1和方案2的参数估计值与真值的差值。方案1和方案2每次的方差估计值分别描绘如图3所示。

表1　LS、WTLS和RTLS估计结果与真值的比较(方案1)

表2　LS、WTLS和RTLS估计结果与真值的比较(方案2)

从表1和图2(a)中不难发现，在不含有粗差的情况下，3种方的参数估计值非常接近，并且与真值的差异几乎相同。但是图3(a)则说明RTLS法得到的方差估计值比LS和WTLS的小，在不含有人为粗差的情况下，一些随机误差较大的点被RTLS法剔除了。

表2和图2(b)说明在含有粗差的情况下RTLS法估计的参数更接近真实值。从表2的最后一列和图3(b)可以发现，此时3种方法得到的方差估计值存在较大的差异，同方案1一样，RTLS计算的方差估计值最小，这说明RTLS法能够有效的剔除粗差。

五、结束语

在将空间直线拟合问题转换成拟合两个相交平面问题后，LS估计没有顾及z坐标轴的观测误差，估计理论不够严密。虽然WTLS法能够解决上述问题，也能够处理系数矩阵中的结构性问题，但是对于含有粗差的情况却无能为力。为了解决这些问题，本文提出了采用RTLS法估计空间直线参数，用非线性拉格朗日乘数法推导了RTLS的计算公式，设计了一种可行的RTLS算法。模拟试验结果证明了本文算法能够有效剔除粗差，提高了参数和验后方差的估计精度。

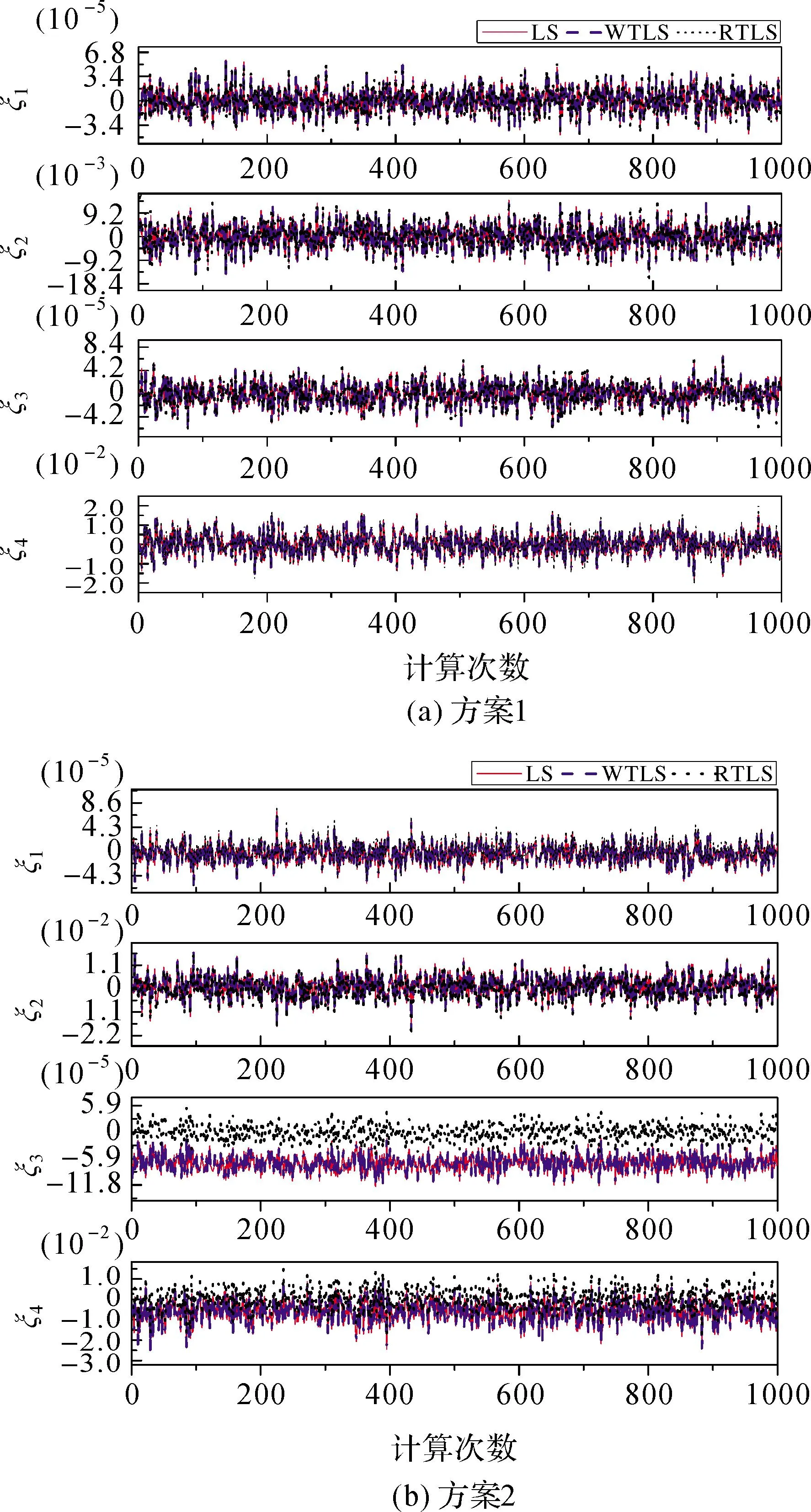
图2　LS、WTLS和RTLS估计参数与真值之差

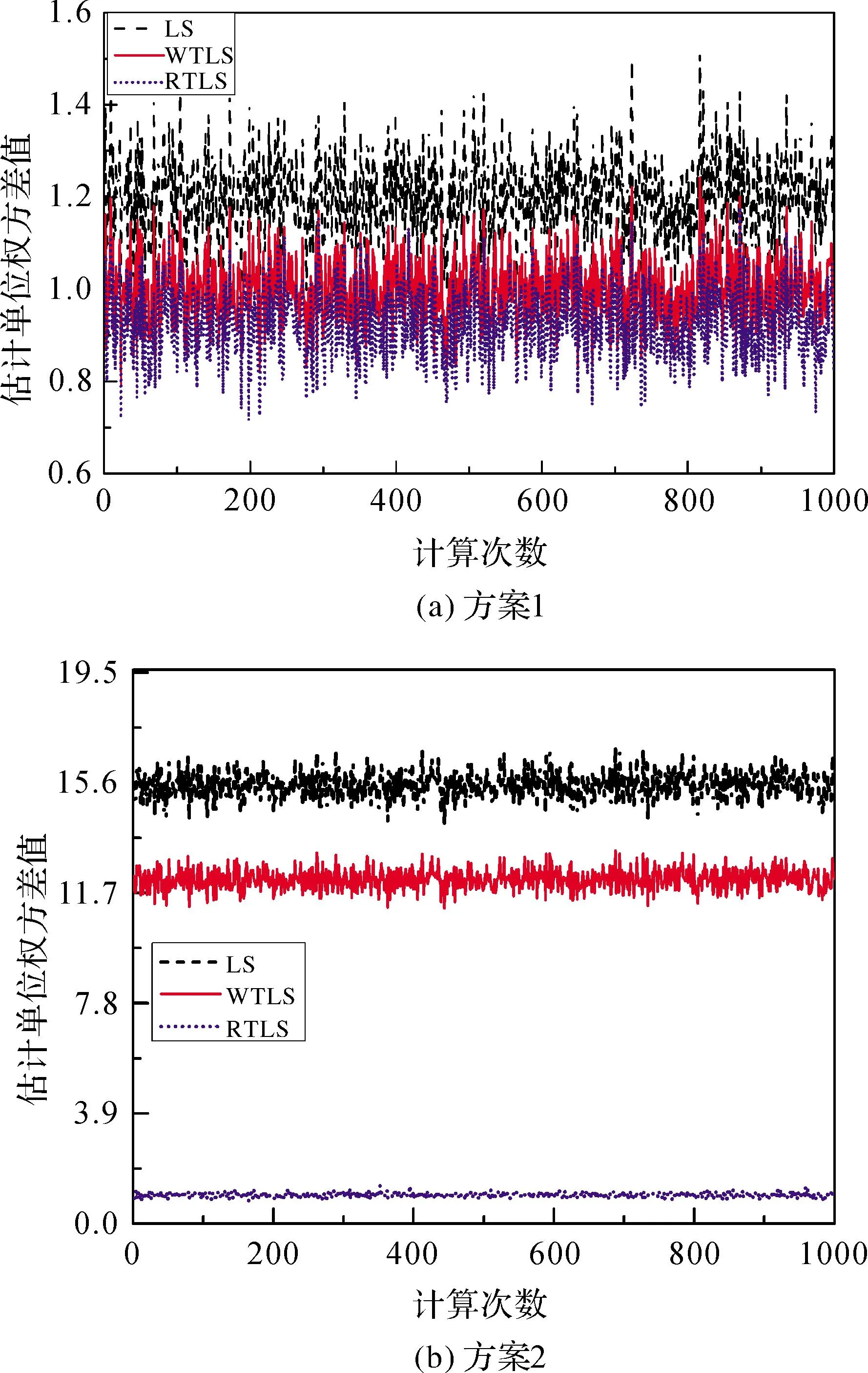
图3　LS、WTLS和RTLS的方差估计值

参考文献：

[1]姚宜斌,黄书华,孔建,等.空间直线拟合的整体最小二乘算法[J]. 武汉大学学报：信息科学版,2014,39(5): 571-574.

[2]袭杨.空间直线拟合的一种方法[J].齐齐哈尔大学学报: 自然科学版,2009, 25(2): 64-68.

[3]王伟锋, 温耐.空间直线拟合研究[J].许昌学院学报, 2010,29(5): 37-39.

[4]郭际明,向巍,尹洪斌.空间直线拟合的无迭代算法[J]. 测绘通报, 2011(2): 24-26.

[5]王解先,季凯敏.工业测量拟合[M].北京:测绘出版社,2008.

[6]陈义,陆珏.以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012, 41(5): 715-722.

[7]李博峰,沈云中.基于等效残差积探测粗差的方差-协方差分量估计[J]. 测绘学报，2011, 40(1): 10-14.

[8]栾学晨，杨必胜，张云菲.基于结构模式的道路网结点匹配方法[J]. 测绘学报， 2013, 42(4): 608-614.