车载激光扫描测量系统整体误差模型建立及其分析

周阳林，王　力，李广云，宗文鹏，王石岩

(1. 信息工程大学导航与空天目标工程学院，河南 郑州 450052； 2. 现代城市测绘国家测绘地理

信息局重点实验室，北京 100000； 3. 河南省基础地理信息中心，河南 郑州 450003)

ZHOU Yanglin，WANG Li，LI Guangyun，ZONG Wenpeng，WANG Shiyan

车载激光扫描测量系统整体误差模型建立及其分析

周阳林1,2，王力1,2，李广云1,2，宗文鹏1，王石岩3

(1. 信息工程大学导航与空天目标工程学院，河南 郑州 450052； 2. 现代城市测绘国家测绘地理

信息局重点实验室，北京 100000； 3. 河南省基础地理信息中心，河南 郑州 450003)

Global Error Model and Accuracy Analysis of MLS

ZHOU Yanglin，WANG Li，LI Guangyun，ZONG Wenpeng，WANG Shiyan

摘要：影响车载激光扫描测量系统的点云定位精度的误差按来源主要分为测量误差、设备安置误差、数据处理误差3类。本文从车载激光扫描测量系统空间基准统一方程出发，推导了车载激光扫描测量系统综合误差模型，并分别研究了激光测距与测角、POS定位与定姿、激光扫描仪的安置参数及尺度因子等对激光脚点定位精度的影响规律。

引文格式： 周阳林，王力，李广云，等. 车载激光扫描测量系统整体误差模型建立及其分析[J].测绘通报，2015(9)：19-23.DOI:10.13474/j.cnki.11-2246.2015.0269

关键词：车载激光扫描测量系统；误差模型；精度分析

中图分类号：P234

文献标识码：B

文章编号：0494-0911(2015)09-0019-05

收稿日期：2014-09-06

基金项目：国家自然科学基金(41274014)；现代城市测绘国家测绘地理信息局重点实验室开放基金(20131204WY)

作者简介：周阳林(1990—)，男，硕士生，主要从事车载移动测量系统检校研究。E-mail：zhouyanglin@126.com

一、引言

随着城市数字化、信息化的飞速发展，移动测量系统(mobile mapping systems, MMS)成为城市空间位置数据获取的重要手段。车载激光扫描测量系统是指在移动测量车上装配位置定位定姿系统(position and orientation system,POS)、激光扫描仪(light detection and ranging, LiDAR)、成像系统(如CCD)等传感器和设备，在载体移动过程中，快速采集道路及两旁地物的点云数据和影像的系统[1]。

MMS是一种复杂的测量系统，其精度一直受到广泛关注。文献[2—3]对机载LiDAR的系统误差进行分析，并建立了机载LiDAR系统误差模型；文献[4]分析了IMU姿态误差对机载LiDAR脚点定位精度的影响，但车载激光扫描测系统与机载系统在测量方式上有所区别；文献[5]对车载LiDAR系统误差模型进行推导，并分析了各项误差对激光脚点定位精度的影响，但其使用模型过于简化。

针对以上问题，本文以机载LiDAR系统误差模型为基础，从车载激光扫描测量系统定位方程出发，结合车载激光扫描系统中的测量误差与安置误差，推导了车载激光扫描测量系统整体误差模型，并分析各项误差对激光脚点定位精度的影响规律。

二、定位方程

车载激光扫描测量系统在工作过程中，将激光扫描仪所获得的目标点的角度和距离信息，通过一系列坐标转换，得到其在相应坐标系下的坐标。这些坐标系分别是：激光扫描仪坐标系L、惯性平台参考系I(与载体坐标系固连)、当地水平坐标系LH、地心地固坐标系E、测图坐标系M。各坐标系之间转换过程如图1所示。从直接地理参考[6]的过程中，可得到车载激光扫描测量系统的定位方程

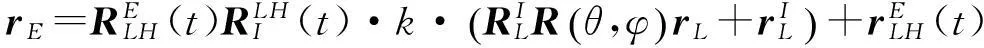
(1)

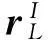
式(1)简化为

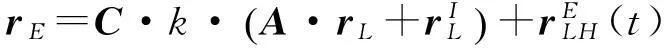
(2)

为更好地分析各项误差对脚点定位精度的影响，将脚点坐标归算至(北东地)测图坐标系进行分析，即

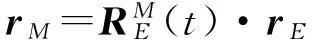
(3)

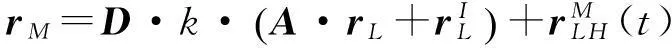
(4)

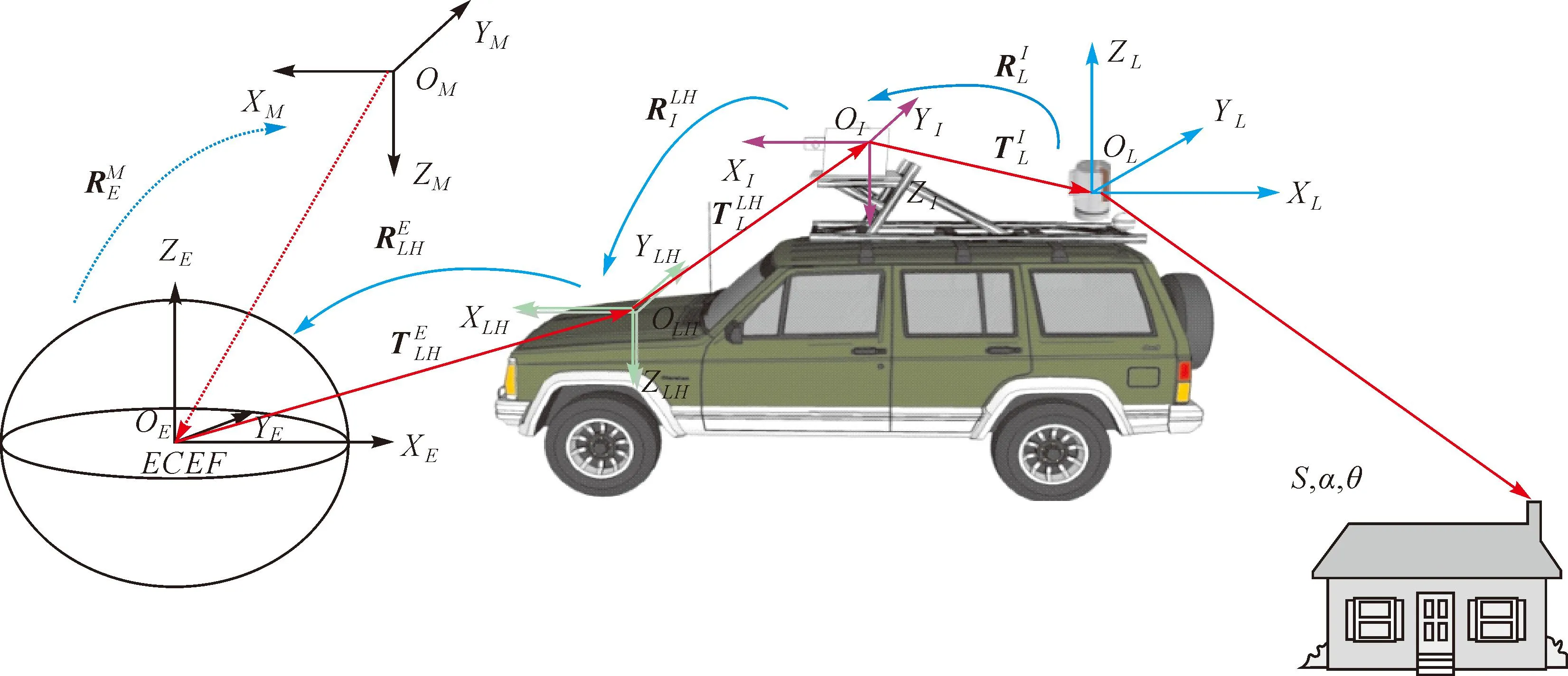
图1　坐标转换示意图

三、误差来源分析

影响车载激光扫描测量系统的误差，按来源可分为3类：测量误差，包括激光扫描仪测距误差、扫描仪测角误差、GNSS定位误差、IMU姿态测量误差；设备安置误差，包括传感器之间的偏心距误差、安置角误差；数据处理误差，包括时间同步误差、内插误差、坐标转换误差。综合各类误差影响，本文主要针对测量误差和硬件安置误差建立综合误差模型。

1. 测量误差

1) 三维激光扫描仪的测量误差：由于仪器本身性能缺陷造成的测量误差，包含激光测距误差及扫描角度测量误差。

2) GNSS定位误差：星历误差(轨道误差)、卫星钟误差、电离层延迟、对流层延迟、多路径效应、接收机钟误差、天线相位中心位置误差会影响GNSS定位，使其产生定位误差。

3) IMU姿态测量误差：当POS系统工作时，IMU输出的是惯性平台参考系相对于当地水平参考系的姿态角。IMU 姿态测量的精度会受到加速度计比例误差、速度计常数误差、随机漂移、陀螺各种系统漂移等因素的影响。

2. 设备安置误差

1) 偏心距误差：是仪器坐标系之间的平移误差。由于各仪器所采用的坐标系中心不同，在安置后需对其位置关系进行精确测定，在测定过程中存在一定的误差。

2) 安置角误差：是仪器坐标系之间的角度误差，由于安置过程中各仪器坐标系不平行而产生的误差。

3. 数据处理误差

1) 时间同步误差：车载激光扫描测量系统由多个子系统组成，子系统间相互独立。由于子系统时间起点不同，时间基准不同，数据在传输时产生延时，造成各传感器输出数据时间不同步[7]。

2) 内插误差：车载激光扫描测量系统各子系统的输出频率不一致，POS的输出轨迹频率为200 Hz，而激光扫描仪输出频率为200 kHz，为得到每次扫描时刻对应的载体的位置和姿态信息，需要对组合导航输出的轨迹数据进行插值计算，由插值算法带来的误差称为插值误差[8]。

3) 坐标转换误差：为获得目标点在相应坐标系下的坐标，需要进行系列坐标转换，在坐标转换过程中出现的误差称为坐标转换误差。本文主要讨论因坐标基准不同，在坐标转换过程中存在尺度变换而产生的误差，称为尺度因子误差[9]。

四、误差模型分析

对式(4)进行微分运算，可得误差传播计算公式

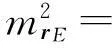
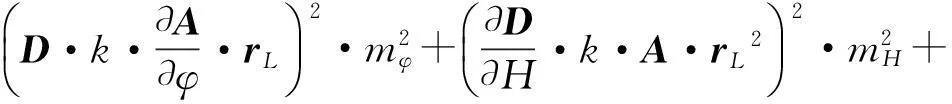
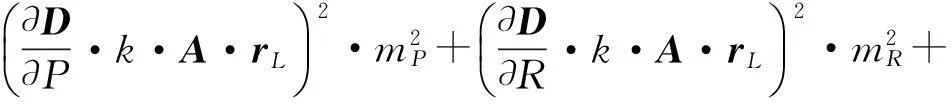
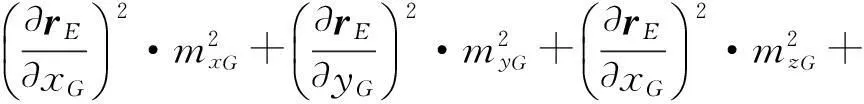
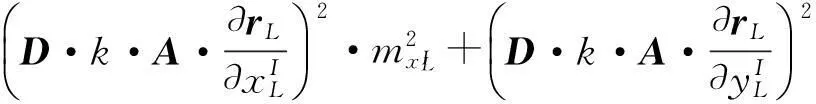
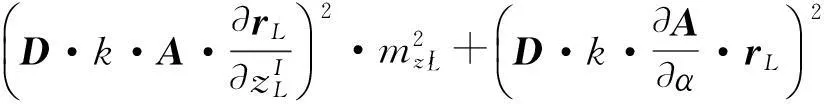
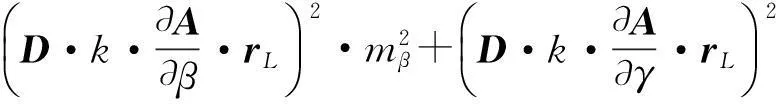
(5)

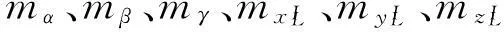
1. 测量误差分析

对测量误差进行分析时，假设激光扫描仪测距误差为0.005 m，垂直扫描角θ误差为0.000 9°，水平扫描角φ误差为0.000 9°；POS系统定位误差分别为0.02 m、0.02 m及0.05 m；姿态测量误差为偏航角、俯仰角及横滚角的测量精度误差，分别为0.025°、0.02°及0.02°。

(1) 激光测距误差对脚点定位的影响

由图2可知，激光扫描仪测距误差对脚点的激光脚点航向定位精度影响较小，对脚点旁向、高程方向定位精度影响较大；对脚点定位精度的影响存在周期性。

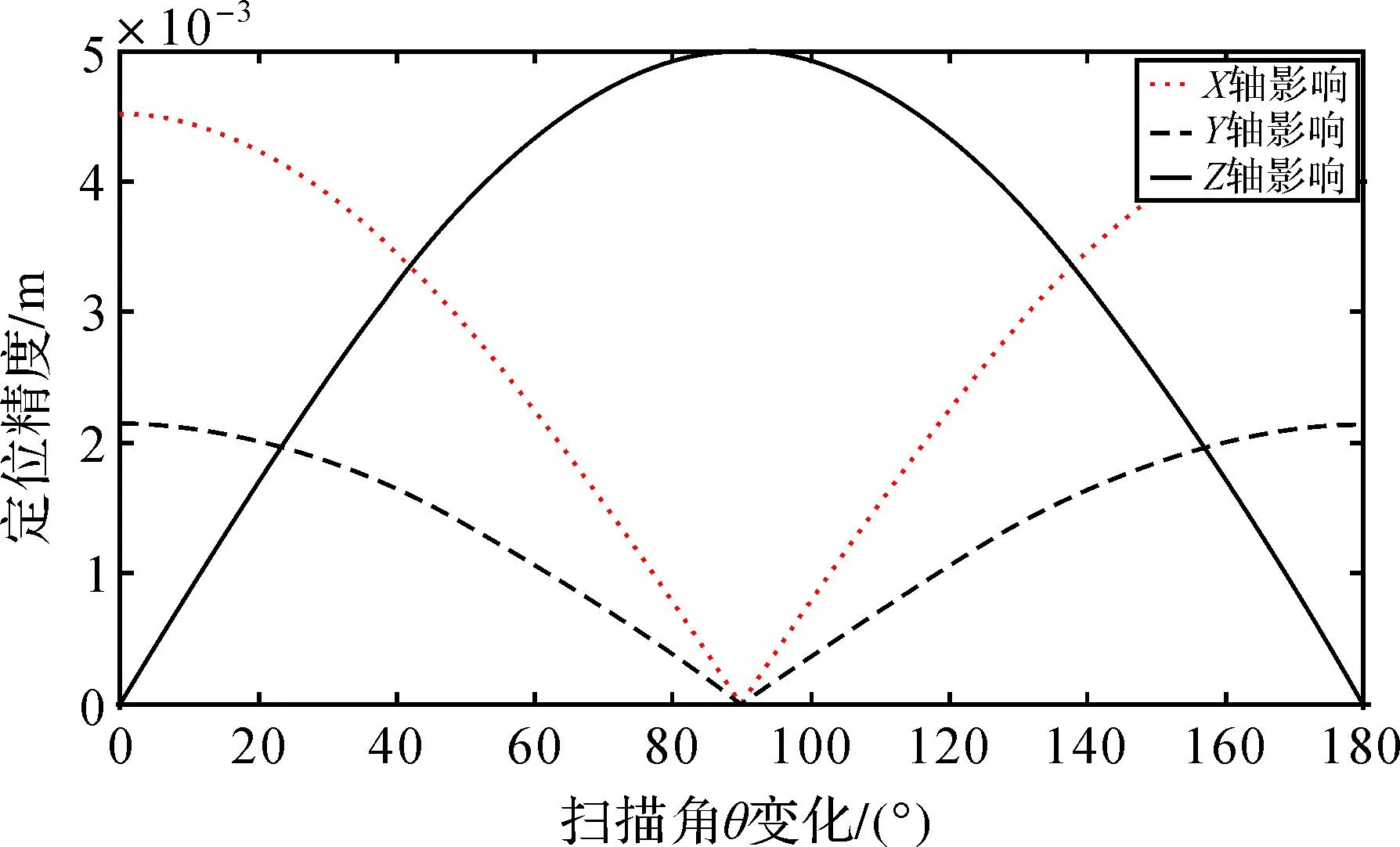
图2　测距误差对脚点定位影响

(2) 垂直扫描角θ误差对脚点定位的影响

由图3可知，激光扫描仪垂直扫描角θ误差对激光脚点航向定位精度影响较小，对其高程、旁向定位精度影响较大。

图3　扫描角θ误差对脚点定位影响

(3) 水平扫描角φ误差对脚点定位的影响

由图4可知，激光扫描仪扫描角φ误差对脚点的高程定位精度影响较小，对激光脚点旁向、旁向轴定位精度影响较大。

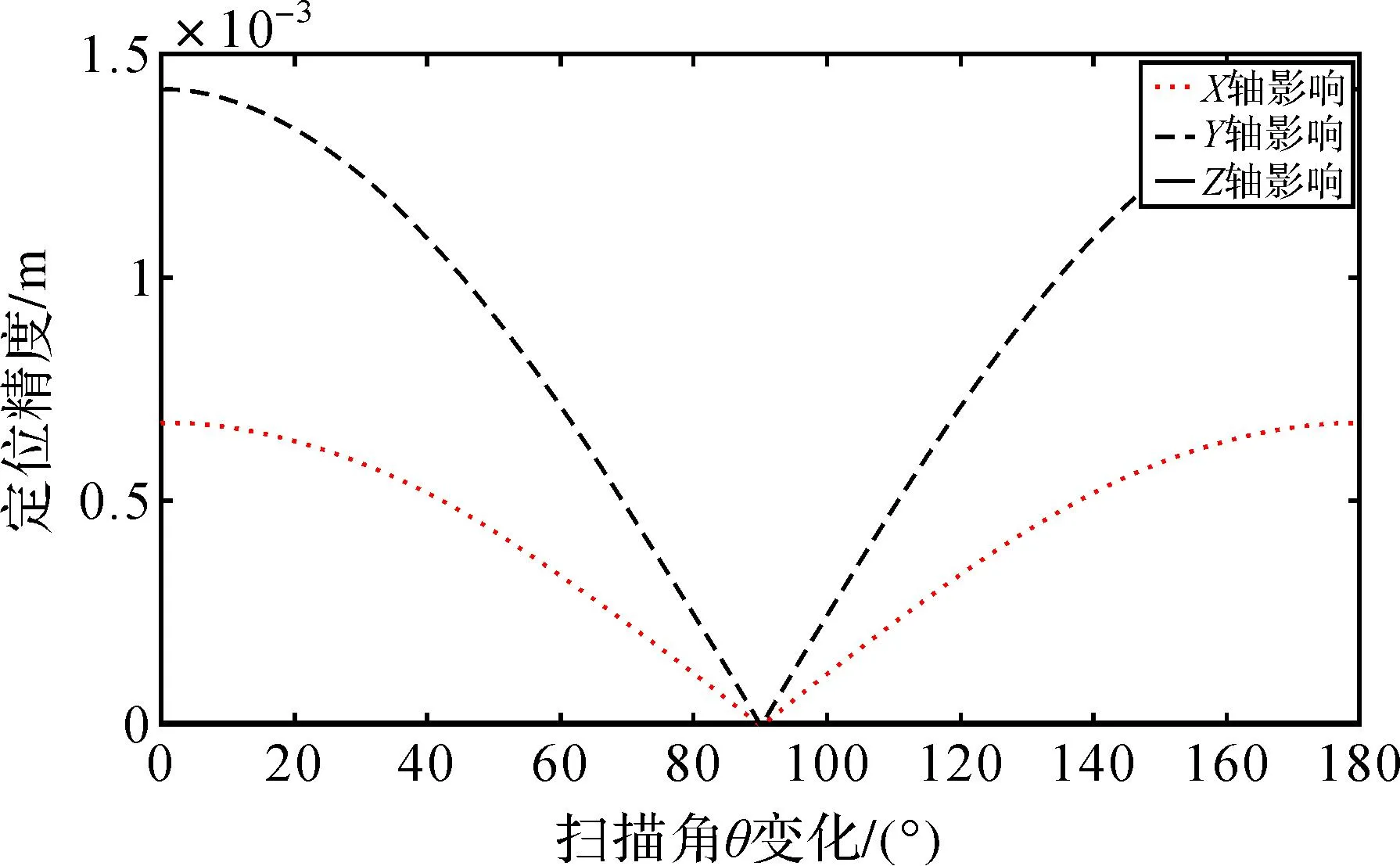
图4　扫描角φ误差对脚点定位影响

(4) POS定位误差对脚点定位的影响

由图5可知，POS定位误差对激光脚点定位误差的影响关系是直接传递的。

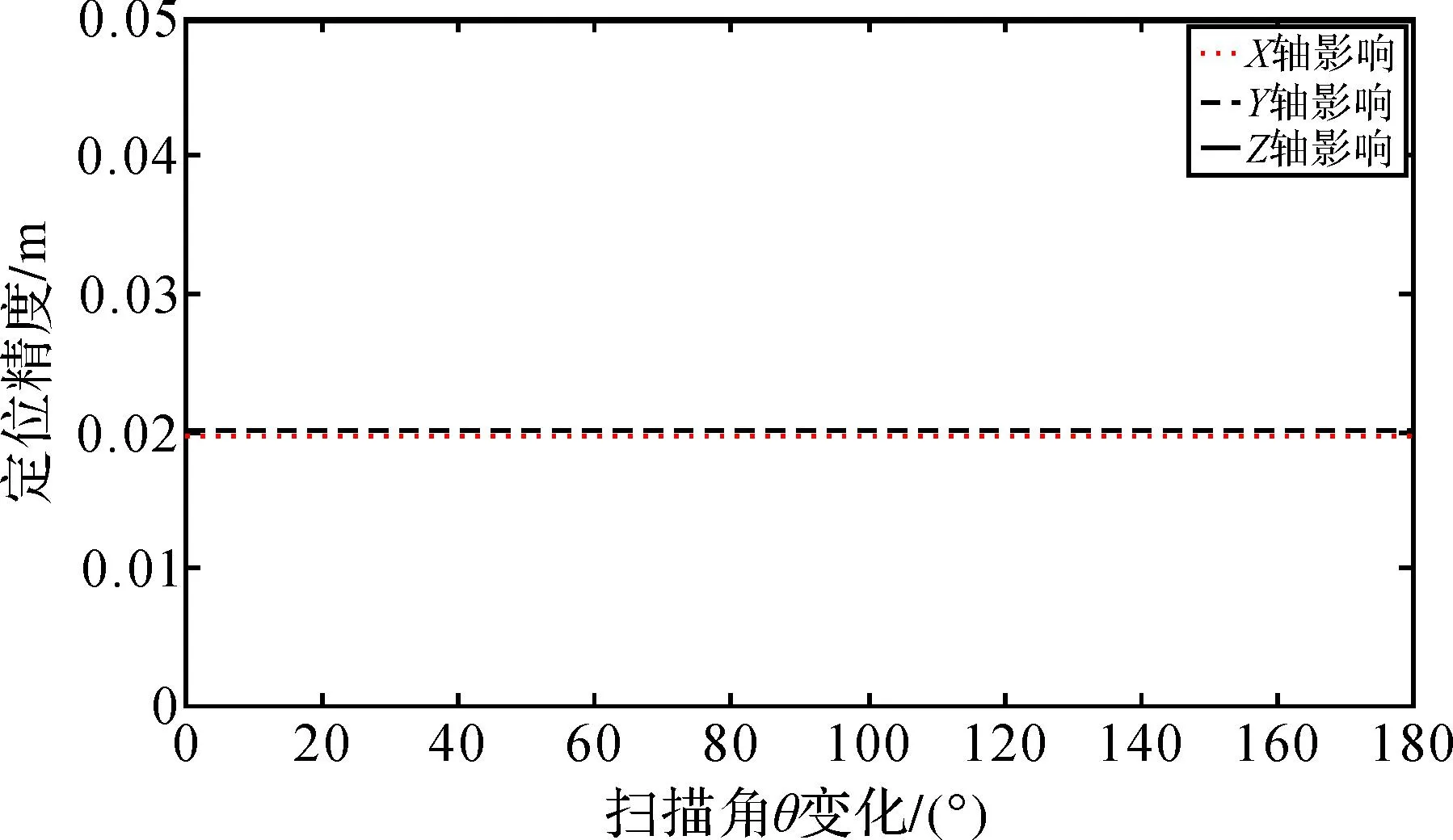
图5　POS定位误差对脚点定位影响

(5)POS定姿误差对脚点定位的影响

由图6、图7、图8可知，随着扫描角θ的变化，姿态测量误差对脚点定位的影响存在周期性。航向角误差对脚点航向、旁向定位精度影响较大，对高程方向定位精度影响较小；俯仰角误差对脚点航向、高程定位精度影响较大，对旁向定位精度影响较小；横滚角误差对脚点高程、旁向定位精度影响较大，对航向定位精度影响较小。

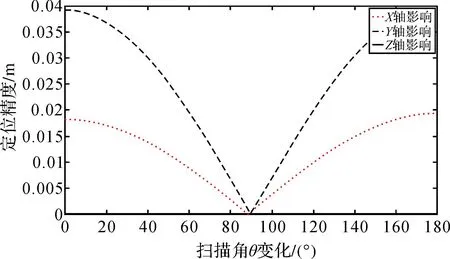
图6　航向角误差对脚点定位影响

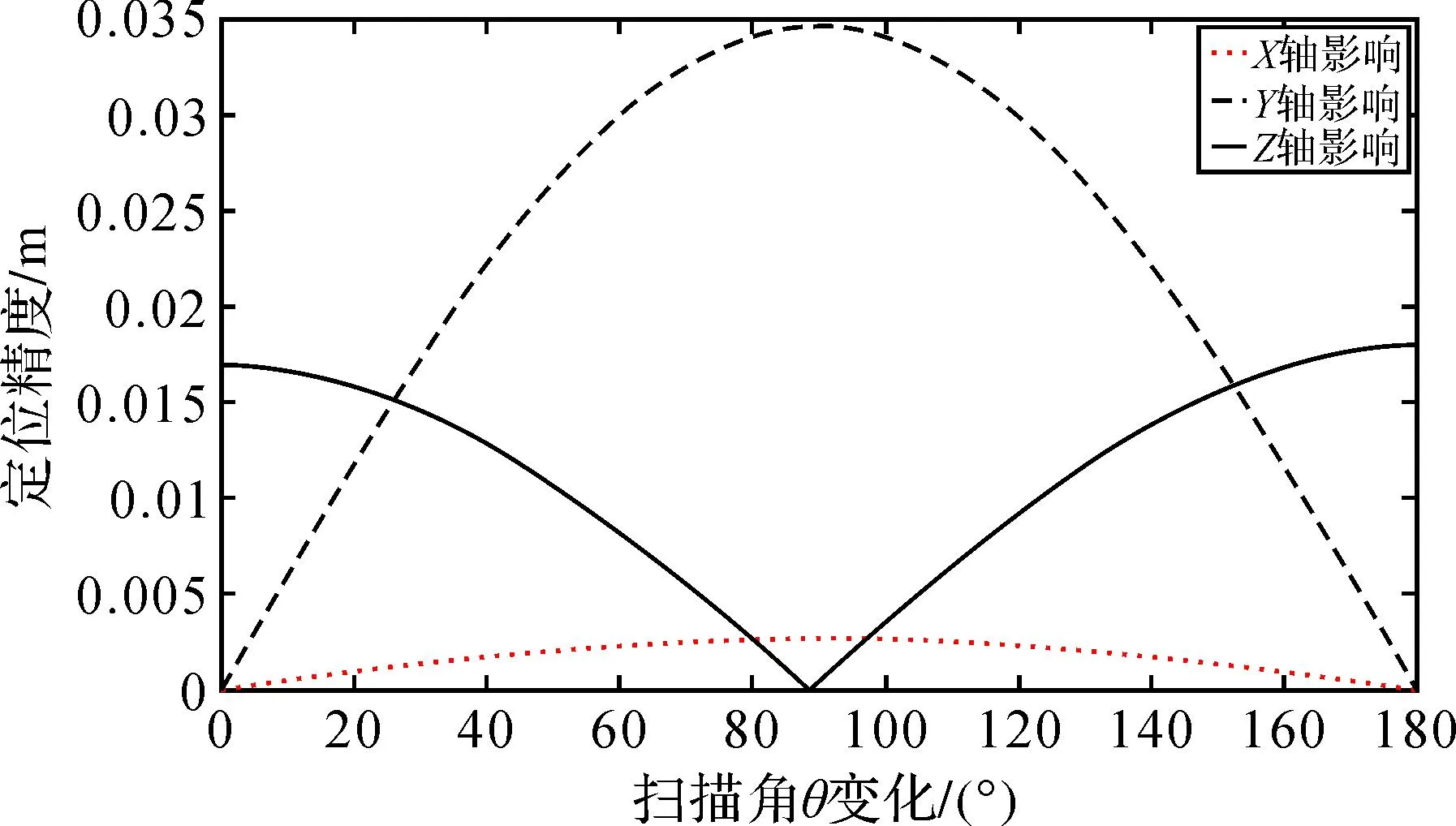
图7　俯仰角误差对脚点定位影响

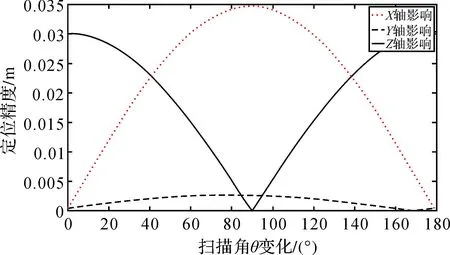
图8　横滚角误差对脚点定位影响

2. 设备安置误差分析

对安置误差进行分析时，假设在载体坐标系下，安置角α、安置角β及安置角γ的角度误差均分为0.01°，X、Y、Z三轴的偏心量误差均为0.02 m。

(1) 安置角对脚点定位的影响

从图9、图10、图11可知，随着扫描角θ的变化，安置角误差对脚点定位的影响存在周期性。安置角α误差对脚点旁向、航向定位精度影响较大，对高程方向定位精度影响较小；安置角β误差对其旁向、高程定位精度影响较大，对航向定位精度影响较小；安置角γ误差对航向、旁向定位精度影响较大，对高程方向定位精度影响较小。

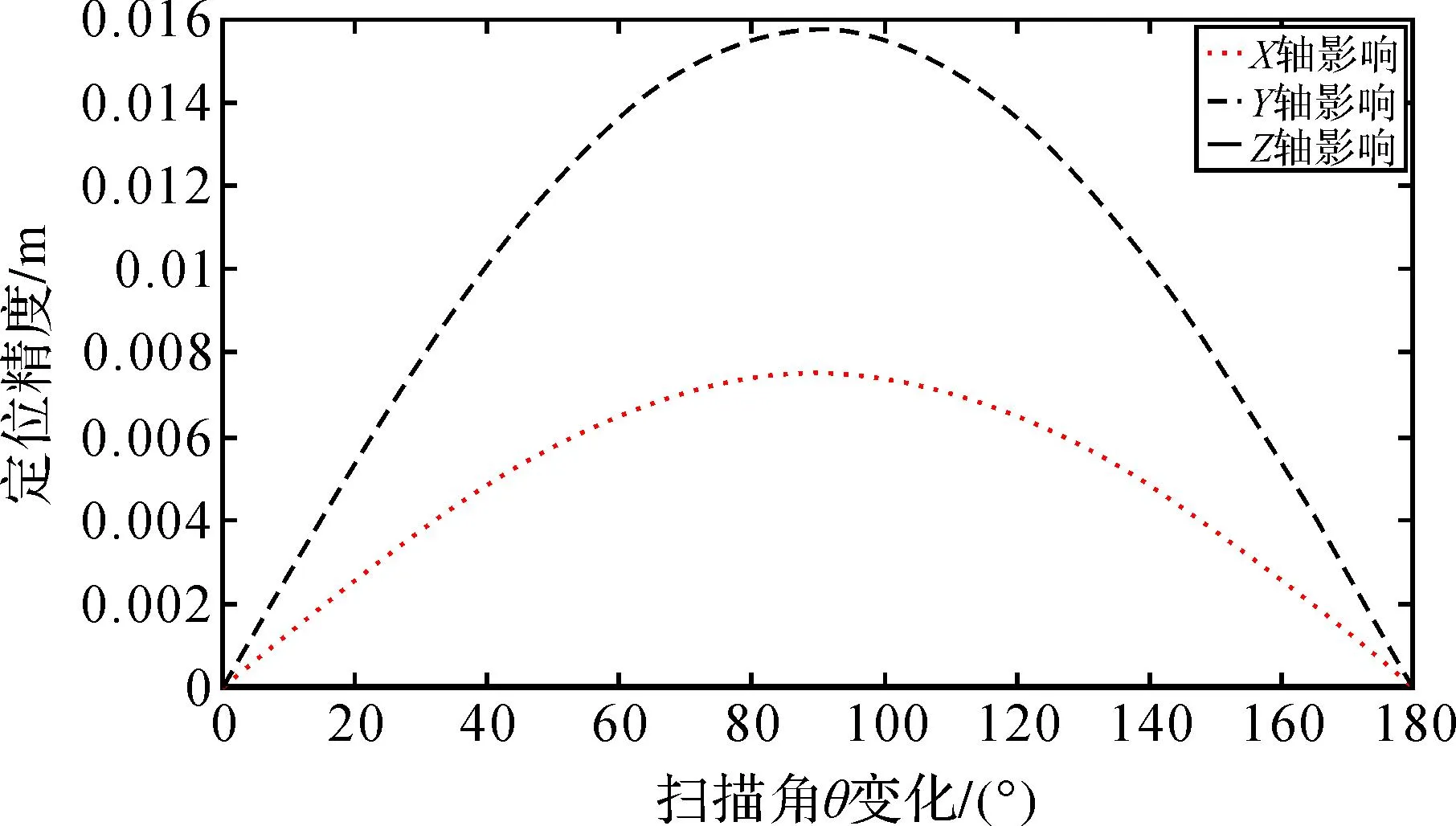
图9　安置角α误差对脚点定位影响

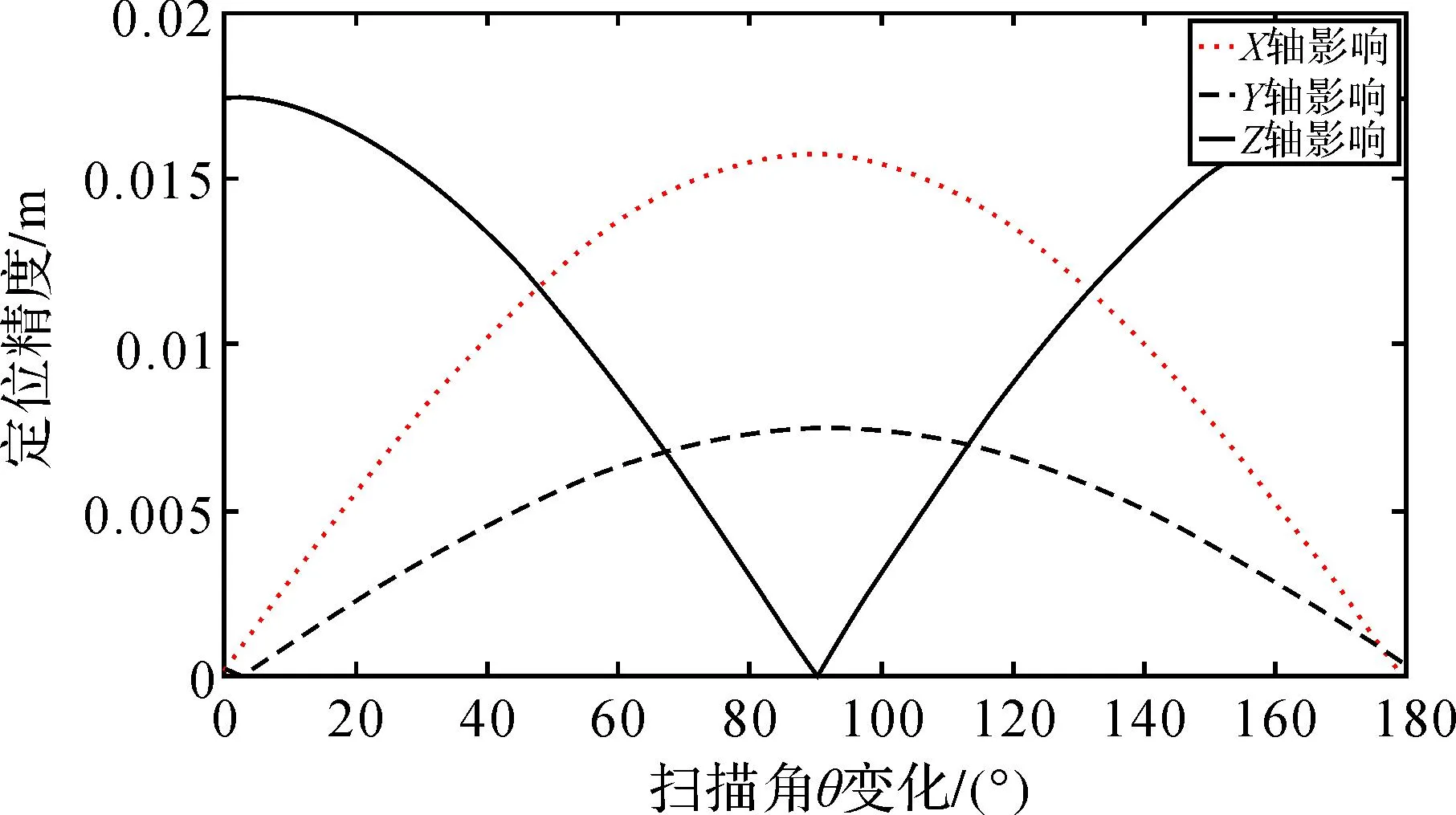
图10　安置角β误差对脚点定位影响

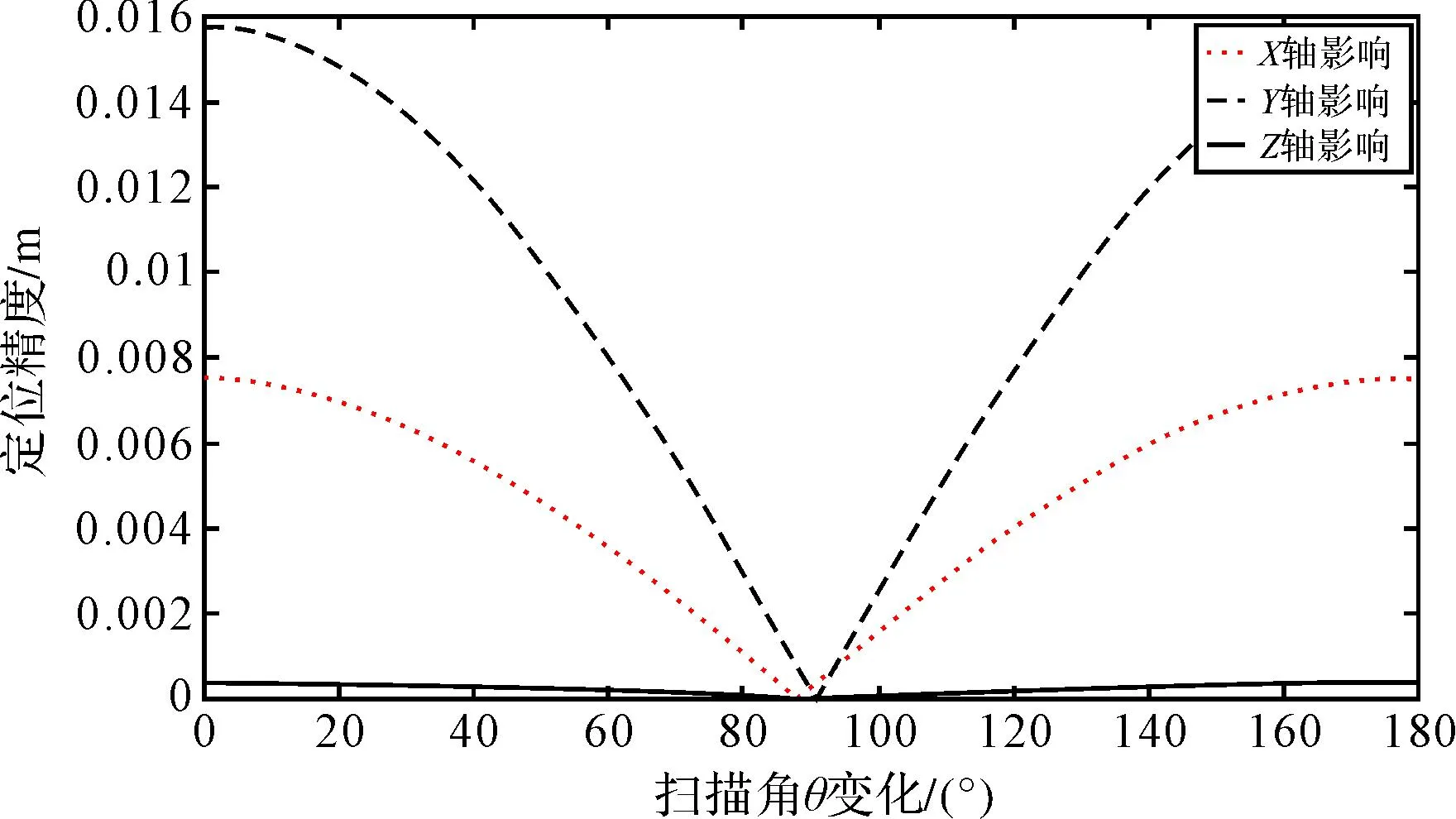
图11　安置角γ误差对脚点定位影响

(2)偏心量对脚点定位影响

从图12、图13、图14可知，随着扫描角θ的变化，偏心量对脚点定位精度的影响是定值。X轴偏心量误差对脚点航向定位精度影响较大；Y轴偏心量误差对脚点旁向定位精度影响较大；Z轴偏心量误差对脚点高程方向定位精度影响较大。

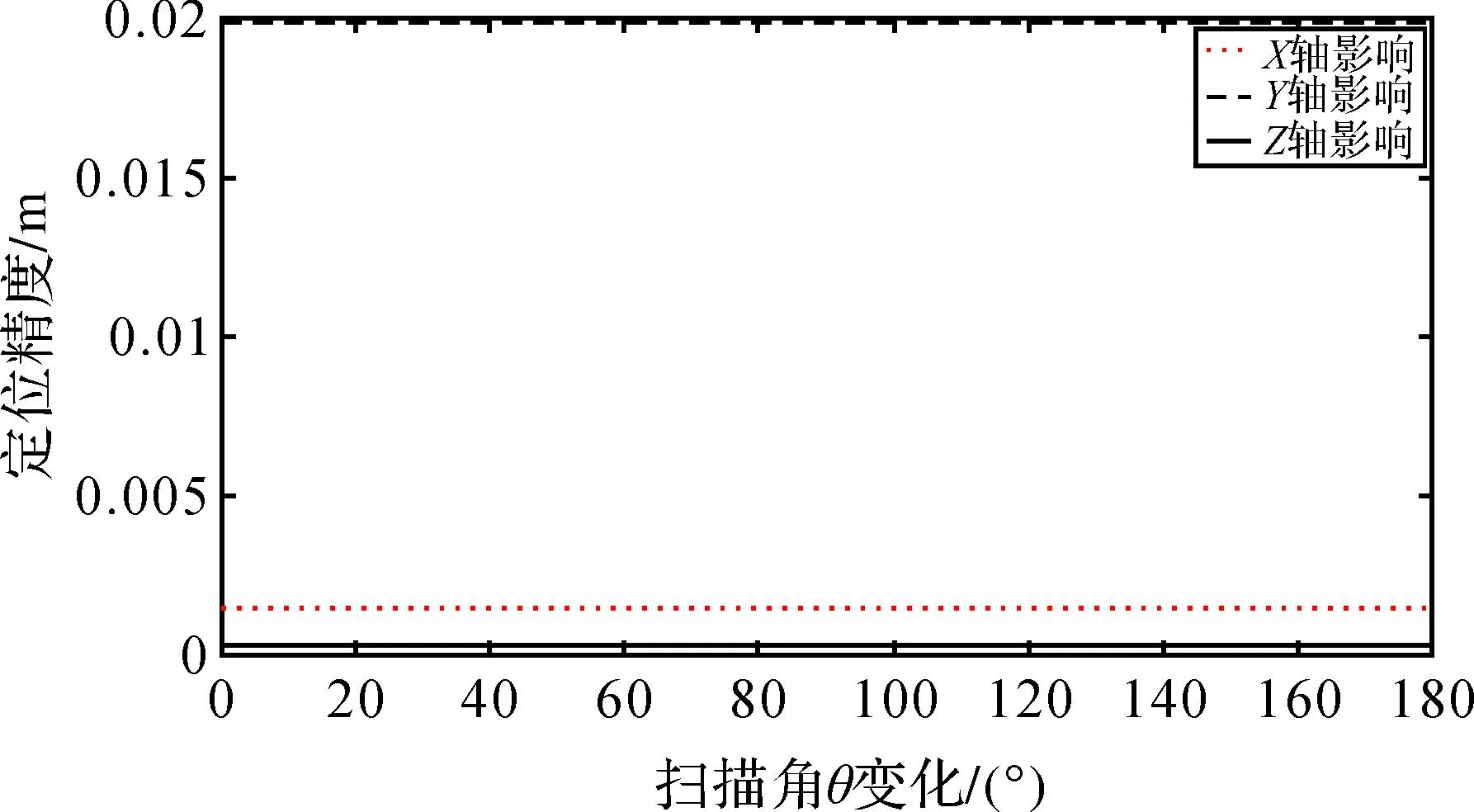
图12　X轴偏心矢量误差对脚点定位影响

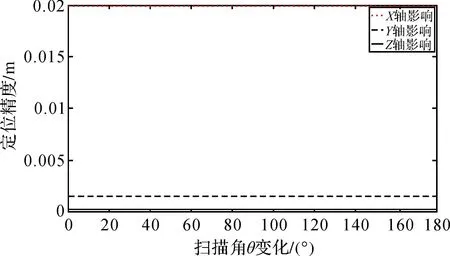
图13　Y轴偏心矢量误差对脚点定位影响

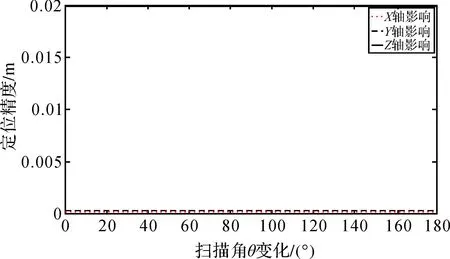
图14　Z轴偏心矢量误差对脚点定位影响

3. 坐标转换误差分析

主要为尺度因子误差对激光脚点定位的影响，假设尺度因子的误差为20×10-6D。

从图15可知，随着扫描角θ的变化，尺度因子误差对脚点定位精度的影响存在周期性。尺度因子误差对脚点在旁向、高程方向定位精度影响较大，对其在航向定位精度影响较小。

图15　尺度因子误差对脚点定位影响

五、模拟数据分析

试验时，车载激光扫描测量系统采用三维扫描的模式。选取自东向西的一段车行轨迹作为基础，模拟一条扫描范围为100 m，扫描角θ从0°～180°变化，扫描角φ为0°的扫描线(如图16所示)。

模拟轨迹数据说明见表1—表4。

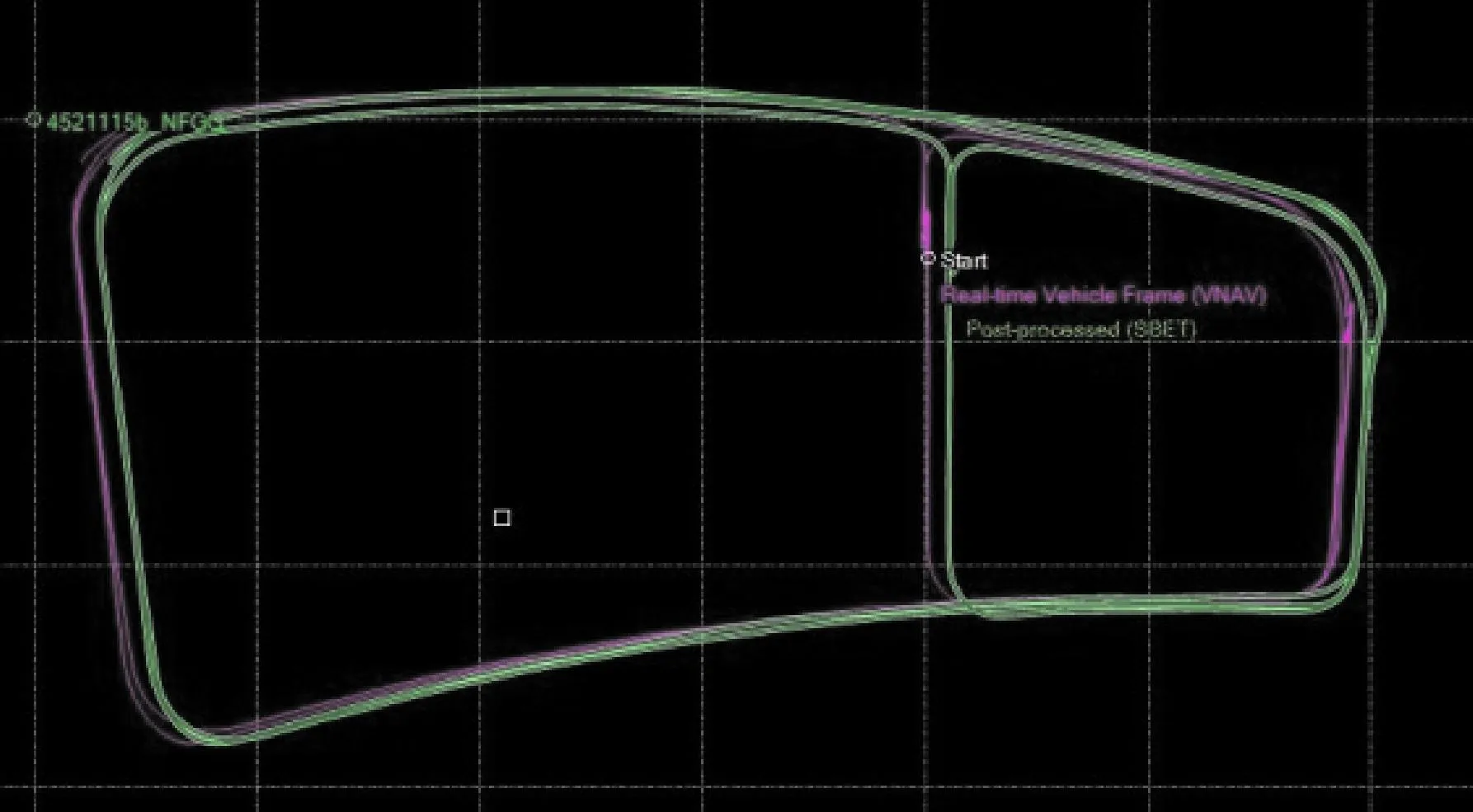
图16　跑车轨迹图

经度纬度大地高113°33'55.888632″34°49'10.207956″91.948m

表2　姿态参数

表3　安置角参数

表4　偏心量参数　m

按模型计算所得所得脚点定位误差在水平方向达到0.048m，高程方向达到0.062m，与实际未检校前系统测量精度相符。

六、结束语

车载激光扫描测量系统脚点定位精度与许多因素有关，如激光扫描仪的测距、测角误差，POS系统的定位、定姿误差，设备安置误差，尺度因子误差等。本文系统分析了各误差因子对脚点定位精度的影响。由模型推导可知，激光脚点可达到厘米级的点位精度，与实际测量值相符。下一步，为了获得更高精度测量，可提高设备加工工艺，减小POS定位定姿误差、硬件安置误差；在误差模型基础上，对安置参数进行校准；针对水平方向、高程误差影响，建立误差改正模型，进一步消除系统误差影响。

参考文献：

[1]李德仁．移动测量技术及其应用[J]．地理空间信息，2006，4(4)：1-5．

[2]CHANTO.Feature-basedBoresightSelf-CalibrationofaMobileMappingSystem[EB/OL]. (2011-09-02)[2014-05-01].http:∥www.ucalgary.ca/engobdocs/MJC/11.20348_TingOnChan.pdf．

[3]王丽英．面向航带平差的机载LiDAR系统误差处理方法研究[D]．阜新：辽宁工程技术大学，2011．

[4]刘经南，张小红，李征航．影响机载激光扫描测高精度的系统误差分析[J]．武汉大学学报：信息科学版，2002，27(2)：111-117．

[5]李鑫，李广云，王力，等．移动测量系统整体误差模型推导及精度分析[J]．测绘工程，2012，4(2)：23-24.

[6]王力，李广云，杨凡，等．车载3维激光扫描系统安置参数一站式标定方法研究[C]∥第二届全国激光雷达大会论文集.北京:[s.n.],2013: 32-38．

[7]肖进丽，潘正风，黄声享．GPS/INS组合导航系统时间同步方法研究[J]．测绘通报，2007(4)：27-30．

[8]姚吉利.3维坐标转换参数直接计算的严密公式[J].测绘通报，2006(5)：7-10．

[9]冯有前.数值分析[M]．北京：清华大学出版社，2005．

[10]李鑫．车载移动测量系统误差分析与检校方法研究[D]．郑州：信息工程大学，2012．

[11]袁修孝，杨芬，赵青，等．机载POS系统视准轴误差检校[J]．武汉大学学报：信息科学版，2006，31 (12)：1039-1043．

[12]李广云，李宗春．工业测量系统原理与应用[M]．北京：测绘出版社，2011．

[13]房建成，杨胜，刘百奇．高性能POS及其在移动测图系统中的应用[J]．红外与激光工程，2007，36(9)：478-482．

[14]隋立芬，宋力杰，柴洪洲．误差理论与测量平差基础[M]．北京：测绘出版社，2010．