基于稀疏脉冲反演的墙体参数研究

费翔宇，冯温雅，王成浩

(中国电波传播研究所,　山东 青岛 266107)



基于稀疏脉冲反演的墙体参数研究

费翔宇，冯温雅，王成浩

(中国电波传播研究所,山东 青岛 266107)

摘要：稀疏脉冲反演实际上是从含有噪声的雷达数据单道中计算出具有稀疏分布特性的反射系数。文中以范数约束为基础，提出L1范数约束求解的方法，并且采用迭代重加权最小二乘法(IRLS)的优化算法，该算法具有精度高、速度快的优点，对穿墙侦查雷达数据处理后可以有效提高分辨率，获得反射系数，有助于进一步求得墙体的厚度和介电常数。最后针对不同数据的实验结果验证了算法的有效性。

关键词：稀疏脉冲反演；迭代重加权最小二乘法；反射系数；介电常数

0引言

穿墙侦查雷达采用超宽带电磁波穿透墙体对室内人体目标进行探测定位，广泛应用于城市巷战、反恐作战和灾害救援等军事和民事领域。穿墙侦查雷达可以对建筑物遮挡的目标进行探测，但由于电磁波在传播过程中会发生衰减、频散和其他干扰，这些因素都影响雷达的探测效果。在实际探测中，如果能够对建筑物结构进行反演，便可以提高雷达的探测准确性，增加实用性，提高反恐和救援的成功率。对建筑物结构的反演主要通过对建筑物结构介质分层界面的探测，通过探测到的建筑物结构反射系数推导出墙体的结构厚度和介电常数等参数[1-3]。在信号中反射系数的获取中主要通过对数据进行反褶积的方法进行处理。反褶积是提高雷达信号信噪比和分辨率的一种重要方法，可以有效得到反射系数信息。目前已经有很多反褶积方法应用于雷达信号处理，如传播反褶积、预测反褶积、混合相位反褶积和双边反褶积等。由于雷达信号的反射系数是稀疏的，所以本文采用建模能力强、地质条件适应性强的稀疏脉冲反演(稀疏脉冲反褶积)的方法得到反射系数[4-5]。

稀疏性作为信号的一种很有吸引力的特征，赋予地震信号处理新的生命力，为许多地震资料处理问题的解决提供了便利，促进了地震数据的噪声压制以及反射系数反演，本文将这种特征引入到穿墙雷达探测的信号处理中。

对于信号x=[x1,x2,…,xN]，如果只有l(lN)个样点为非零值，而绝大部分样点值为零，则该信号为严格稀疏的，该信号称为l-稀疏信号。虽然本文中具有多层墙体结构，但是墙体反射系数依然是稀疏的。因此由墙体反射信号得到反射系数序列的过程就是恢复其稀疏性的过程，所采用的变换要有较好的稀疏表示能力，稀疏脉冲反演就可以通过较少的系数有效地表示反射信号的主要特征，并且能较好地压制噪声，提高分辨率。

1方法原理

探地雷达信号的褶积模型可以表示为

s(t)=w(t)*r(t)+n(t)

(1)

式中：s(t)为记录的雷达信号；w(t)为雷达子波；r(t)为反射系数；n(t)为随机噪声；*表示褶积运算。

式(1)无法表示信号频率随时间的变化，因此将其拓展为下式

(2)

将式(2)写为矩阵的形式为

s=Wr+n

(3)

式中：W是子波矩阵；r是反射系数向量；n是噪声向量。

由于W是不可逆的，在不考虑噪声的情况下，需要W的共轭矩阵来求解r

r=WHW-1-Ws

(4)

WHW是可逆的，式(4)等价于求一个最小二乘问题[6-7]。

由于最小二乘解可能会产生很大的范数并影响求解的结果，所以必须用正则化条件来降低多解性，不同的约束条件具有不同的效果，本文要求解具有稀疏性，因此需要使用稀疏约束条件，L0范数可以通过测量非零解的个数来控制稀疏度，但是L0范数正则化方法是NP难题，计算困难。在这种情况下可以选择L1范数正则化方法进行约束。L1范数约束反演使成本函数J最小

(5)

式中：λ>0；‖r‖1为L1范数约束项，表示r中所以元素绝对值的和。L1范数通过约束项来产生稀疏度高的解。

L1范数约束反演问题也称为基追踪问题，近年来发展了很多快速算法，包括内拥挤法(In-Crowd)、谱投影梯度法、迭代重加权最小二乘法(IRLS)、快速迭代收缩阈值法、近似信息传递方法(AMP)、内点算法等，本文采用迭代重加权最小二乘法来对L1范数约束进行快速计算。

无约束优化模型为

(6)

其中，M>0为惩罚因子；d(r)为稀疏性度量函数

(7)

目标函数J的梯度

J(r)=Пr+M[WTWr-WT-s]

(8)

2J(r)=Пr+M·WTW

(9)

所以求解式(6)的牛顿迭代公式为

r(k+1)=r(k)-[2J(r(k))]-1·J(r(k))

(10)

将式(8)和式(9)代入式(10)并整理可得最终迭代公式

r(k+1)=[λПk+WTW]-1WTs

(11)

由式(11)即可迭代得到反射系数[8-10]。

2实验分析

为了验证算法的有效性及信号提取效果，按照实际探测的需要，建立了穿墙侦查雷达探测实验场，实验场地如图1所示，实验时将天线放在图中左边墙体的左侧，墙体厚度为26.5cm，墙体之间间距为3m。穿墙雷达天线主频采用400MHz和1 200MHz两种，采样点数为2 048，时窗为50ns。

图1　实验场地

图2为主频400MHz天线采用直线增益测量所得数据的单道波形，直线增益设置的较小，最大波形为直达波和墙体表面波反射的叠加。

图2　400 MHz处理前单道波形

对采集的数据进行零点调节和自动增益后，单道波形如图3所示，可以看出图中几乎很难分辨出层位信息。我们对图3数据进行本文中介绍的稀疏脉冲反演处理，处理后得到的数据如图4所示，从图中可以看出墙体前后表面能很直观地表现出来。采用主频1 200MHz天线进行探测实验，该探测实验直接采用多点增益的方式进行数据录取，探测得到的原始数据单道波形如图5所示，从单道波形可以看出相对主频400MHz天线虽然测得的层位数据更加清楚一些，但杂波依旧较多，层位仍然难以准确判断。我们对该单道波形进行稀疏脉冲反演处理，得到处理后单道波形如图6所示，图中可以清楚得到墙体的层位信息。

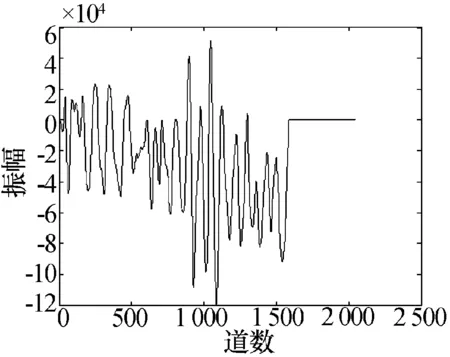
图3　400 MHz预处理单道波形

图4　400 MHz处理后单道波形

图5　1.2 GHz处理前单道波形

图6　1.2 GHz处理后单道波形

在上述分析的基础上，我们可以计算出墙体的厚度和介电常数。其中厚度通过计算处理后数据中墙体前后表面采样点数以及相邻采样点之间间距来求得。求介电常数过程中，通过改变收发天线间距来获得不同的双程走时，这样可以测出收发天线间距为x1、x2时的双程走时为t1、t2，则介电常数为

(12)

式中：c为电磁波在空气中的波速，用该公式求得介电常数可以去除厚度对介电常数的影响。我们通过不同收发天线间距求得的厚度和介电常数如表1所示。实验用墙体厚度为26.5cm，墙体采用砖砌而成，介电常数在9左右。可以看出表1中求得的墙厚和介电常数的误差在可以接受的误差范围内，结果较为准确。

表1　实验结果

3结束语

本文运用了稀疏脉冲反演的方法求取墙体参数，并通过迭代重加权最小二乘法进行快速计算。实验表明该方法可以提高分辨率，获得反射系数，求得的墙体的厚度和介电常数误差较小，为后续的废墟结构反演奠定了基础。但是该方法运算速度还有待进一步优化，在接下来的工作中，如果能提高该方法的运算速度，将更加有效地进行大规模数据处理。

参 考 文 献

[1]罗群，周万幸，马林. 世界地面雷达手册[M]. 北京:国防工业出版社，2005．

LUO Qun, ZHOU Wanxing, MA Lin．World ground radar handbook[M]． Beijing: National Defense Industry Press，2005．

[2]吴晓鸥．新型炮位侦察雷达[J]．外国炮兵，2002(9): 31-36．

WU Xiaoou. A new type emplacement reconnaissance[J]．Foreign Artillery, 2002(9): 31-36．

[3]张光义. 相控阵雷达系统[M]. 北京:国防工业出版社，2006．

ZHANG Guangyi．Phased array radar[M]．Beijing: National Defense Industry Press，2006.

[4]王君超，费翔宇，郭福强, 等. 穿墙侦察雷达人体目标的定位与跟踪[J]. 现代雷达，2011, 33(11): 10-13.

WANG Junchao, FEI Xiangyu, GUO Fuqiang, et al. Locating and tracking human target by through wall detecting radar[J]. Modern Radar, 2011,33(11):10-13.

[5]王宏, 周正欧, 孔令讲, 等. 超宽带噪声穿墙雷达成像与实验研究[J]. 现代雷达, 2010, 32(6): 46-48.

WANG Hong, ZHOU Zhengou, KONG Lingjiang, et al. UWB through-wall noise radar imaging and experiment study[J]. Modern Radar, 2010,32(6): 46-48.

[6]孟大江，王德利，冯飞，等. 基于Curvelet变换的稀疏反褶积[J]. 石油学报，2013, 34(1): 107-114.

MENG Dajiang, WANG Deli, FENG Fei, et al. Sparse deconvolution based on the Curvelet transform[J]. Acta Petrolei Sinica, 2013,34(1)：107-114.

[7]MAURICIO D. Reweighting strategies in seismic deconvolution[J]. Geophysics Journal International, 1997,129(3): 651-656.

[8]韩利. 高分辨率全谱分解方法研究[D]. 长春：吉林大学，2013.

HAN Li. Research on the methods of high-resolution full spectrum decomposition[D]. Changchun: Jilin University, 2013.

[9]王广新. 基于稀疏约束正则化模型的图像提高分辨率技术研究[D]. 长沙：国防科学技术大学, 2008.

WANG Guangxin. Research on image resolution-enhancement based on regularization models with sparsity constraints[D]. Changsha: National University of Defense Technology, 2008.

[10]杜小勇，胡卫东，郁文贤. 推广的正则化FOCUSS算法及收敛性分析[J]. 系统工程与电子技术，2005, 27(5)：922-925.

DU Xiaoyong, HU Weidong, YU Wenxian. Generalized regularized FOCUSS algorithm and its convergence analysis[J]. Systems Engineering and Electronics, 2005, 27(5)：922-925.

A Study on the Parameter of Wall Based on Sparse Spilke Inversion

FEI Xiangyu，FENG Wenya，WANG Chenghao

(China Research Institute of Radio Wave Propagation,Qingdao 266107, China)

Abstract：The sparse reflectivity can be estimated from the noisy A-scan by sparse spike inversion. This paper is used L1norm constrained method, and this method is optimized by Iteratively reweighted least squares (IRLS) which is high in terms of resolution and fast. The resolution can be improved obviously and the reflectivity can be obtained after processed the data of through wall detecting radar used this algorithm, then the thickness and dielectric constant can be obtained. The different experimental result is presented to illustrate the effectiveness of the algorithm at last.

Key words：sparse spike inversion; iteratively reweighted least squares (IRLS); reflectivity; dielectric constant

收稿日期：2015-07-22

修订日期：2015-09-23

通信作者：王成浩Email：wchgpr@163.com

中图分类号：TN957.52

文献标志码：A

文章编号：1004-7859(2015)12-0054-03