一种新的二元Baskakov-Kantorovich算子及其Lp(Δ)逼近
耿 慧,胡晓敏,徐 阳
(杭州电子科技大学数学研究所,浙江 杭州 310018)
一种新的二元Baskakov-Kantorovich算子及其Lp(Δ)逼近
耿慧,胡晓敏,徐阳
(杭州电子科技大学数学研究所,浙江 杭州 310018)
摘要:在二元广义Baskakov算子的基础上定义了一种新的二元非乘积型Baskakov-Kantorovich算子,并且讨论了该算子在Lp空间中的逼近性质,进而利用光滑模给出该算子在Lp空间上的逼近阶。
关键词:Lp(Δ)空间;Baskakov-Kantorovich算子;逼近
0引言
Baskakov算子作为算子逼近的一个重要分支,在函数逼近论中占有重要地位,文献[1]给出了一种推广的Baskakov-Kantorovich算子的逼近性质。随着时间的推移二元Baskakov算子吸引着越来越多学者的关注,其中,文献[2]给出了二元非乘积型广义Baskakov算子的逼近逆定理,文献[3]给出了二元Baskakov算子的加权逼近,文献[4]讨论了多变量的Baskakov算子的加权逼近的估计。此外,还有很多学者研究其组合算子的逼近性质,如文献[5]给出了多元Baskakov-Kantorovich算子的Lp逼近,文献[6]讨论了多变量的Baskakov-Durrmeyer算子的逼近性质。早在1991年,文献[7]中就给出了二元Bernstein-Kantorovich算子且讨论了该算子在Lp空间中的逼近阶,而Baskakov算子是Bernstein算子在无穷域上的一种推广,那么它能否得到类似甚至更好的结果?基于此,本文在二元Baskakov算子的基础上,定义了一种新的二元非乘积型Baskakov-Kantorovich算子,并研究该算子在Lp空间上的逼近性质。
1基本概念

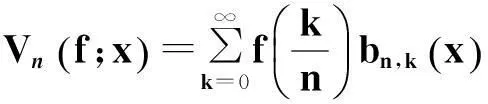
(1)
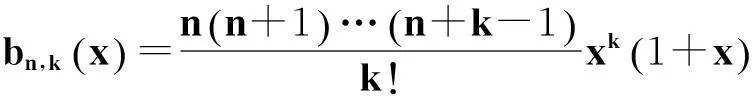
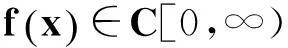

(2)


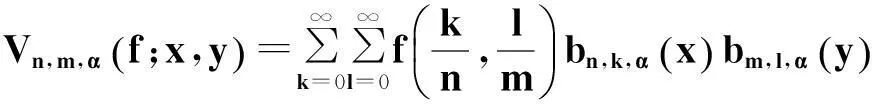
(3)

(4)

(5)
式(3)和式(4)分别为乘积型和非乘积型的二元广义Baskakov算子。
定义4对于任意的f(x,y)∈C(T),定义推广的二元Baskakov-Kantorovich算子[1]:

(6)
定义5对于任意的f(x,y)∈C(T),定义如下二元Baskakov-Kantorovich算子:
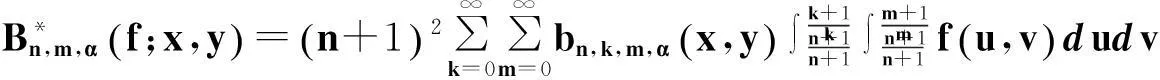
(7)
2主要结果
2.1 辅助引理



2.2 主要结论

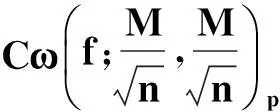
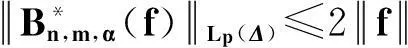

4结束语
本文给出了一种新的推广的二元非乘积型Baskakov-Kantorovich算子,并且研究了该算子在Lp空间上的的基本性质,本文的研究对于研究二元Baskakov-Kantorovich算子的逼近性质等有着重要的意义。
参考文献
[1]高义.一种推广的Baskakov-Kantorovich算子的逼近性质[J].内蒙古大学学报(自然科学版),2013,44(3):234-238.
[2]高义.二元非乘积型广义Baskakov算子的逼近逆定理[J].宝鸡文理学院学报(自然科学版),2010,30(2):13-16.
[3]You G Q,Xuan P C.Weighted Approximation by Multidimensional Baskakov Operators[J].Journal of Mathematical Research & Exposition,2000,20(1):43-50.
[4]Wang J J,Guo H F,Jing J.Estimation of Approximation with Jacobi Weights by Multivariate Baskakov Operator[J].Journal of Function Spaces and Applications,2013,2013:1-6.
[5]Cao F L,Ding C M.Lp approximation by multivariate Baskakov-Kantorovich operators[J].Journal of Mathematical Analysis and Application,2008,348(2):856-861.
[6]Cao F L,An Y F.Lp Approximation by Multivariate Baskakov-Durrmeyer Operator[J].Journal of Inequalities and Applications,2011,28(1):223-236.
[7]盛保怀,吴嘎日迪.一种新的二元Bernstein—Kantorovic算子及其Lp逼近[J].内蒙古师范大学学报(自然科学版),1991,(1):1-6.
[8]陈文忠.算子逼近论[M].厦门:厦门大学出版社,1989:8-75.
[9]Ditzian Z,Totic V.Moduli of Smoothness[M].New York: Springer,1987:24-35.
[10]Zygummd A.Trigonometric Series[M].London:Cambridge University Press,1968:14-39.
A New Multidimensional Baskakov-Kantorovich Operator and ItsLp(Δ) Approximation
Geng Hui,Hu Xiaomin,Xu Yang
(InstituteofMathematics,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
Abstract:On the basis of multidimensional general Baskakov operators,this paper introduces a new multidimensional non-product-type Baskakov-Kantorovich operator,and discusses the approximation properties in Lp spaces.Besides,we investigate the rate of approximation in Lp spaces by taking advantage of the modulus of smoothness.
Key words:Lp(Δ)spaces;Baskakov-Kantorovich operators;approximation
中图分类号:O174.41
文献标识码:A
文章编号:1001-9146(2015)06-0099-04
通信作者:
作者简介:耿慧(1992-),女,安徽亳州人,在读研究生,函数逼近论.胡晓敏副教授,E-mail:mathhuxm@163.com.
收稿日期:2014-12-19
DOI:10.13954/j.cnki.hdu.2015.06.022

