Q460钢基于微观机制的延性断裂判据研究

廖芳芳，王睿智，李文超，周天华

(长安大学建筑工程学院，陕西 西安 710061;)

断裂是建筑结构的一种重要失效模式．目前关于断裂的研究主要采用传统的断裂力学方法，如应力强度因子准则、裂纹尖端张开位移(CTOD)准则和J积分准则．由于它们均假定裂纹已经存在，且在初始裂纹尖端存在高应变约束，因此主要适用于研究脆性断裂或局部塑性损伤程度极其有限的伪脆性断裂问题[1]，而对强震作用下构造无明显缺陷部位发生较大尺度屈服时（裂纹尖端钝化）的延性断裂问题并不适用[2]．此外由于传统断裂力学未考虑应力的三轴性因素，也无法适用于以三向应力状态为主的节点断裂问题．

与这些传统的断裂力学方法相比，基于微观机制的断裂模型能抓住应力应变场对断裂预测的影响，它们能准确预测大范围屈服和无初始裂纹情况下的延性裂纹开展[3]．适用于单调荷载作用下的断裂预测的微观机制模型有Hancock和Mackenzie[4]提出的应力修正临界应变模型（Stress Modified Critical Strain model，简称SMCS）以及Rice和Tracey[5]提出的空穴扩张模型（Void Growth Model，简称VGM）．Kanvinde和Deierlein[6-8]通过对螺栓节点和狗骨节点进行12个拉板试验和有限元分析验证了SMCS和VGM模型能准确预测钢结构节点在单调荷载作用下的延性断裂．后Kanvinde和Fell等[9]又进行了24个用角焊缝连接的十字形试件的单向拉伸试验，分别用传统断裂力学J积分方法和基于微观机制的SMCS方法预测了试件的断裂变形，结果表明相对于J积分方法，SMCS方法能较准确地预测结构角焊缝的断裂变形，而J积分方法偏保守，尤其对于韧性较大的角焊缝材料，在断裂前大范围屈服，J积分结果与试验结果差别较大，SMCS方法更显示其预测结果的准确性．然而，以前关于微观机制模型应用的研究主要是针对母材和钢支撑的，而关于微观机制模型用于预测焊接节点断裂的研究还较少．为使微观机制模型能用于预测焊接节点的延性断裂，本文进行了一系列材料试验和有限元分析以及断口扫描电镜试验以校准有广泛应用前景的国产高强度Q460钢材的微观机制模型参数．试验试件由Q460钢母材和熔敷金属两种材料制成．用自编的VUMAT子程序，分别以校准的SMCS和VGM模型为断裂判据，分析了18个圆周平滑槽口单向拉伸试件的开裂全过程，得到了裂后荷载位移曲线，将其与试验结果进行了对比，验证了SMCS和VGM模型用于节点裂后路径分析的可行性．

1 基于微观机制模型的理论

金属的延性断裂机制通常表现为空穴形核、扩张和聚合的演变过程，如图1所示[3]．基于该机制的微观断裂模型和判据同时描述了应力三轴度和塑性应变对空穴扩张及裂纹开展的影响．根据Rice提出的VGM判据，当应力应变历史的积分达到临界值η时，即可预测发生了断裂．它对应于空穴扩张到足够大，超过临界空穴尺寸，使空穴间发生不稳定收缩导致空穴聚合和裂纹开展．VGM判据的数学表达式如下：

其中：mσ是静水应力，eσ是等效应力或Mises应力，是应力三轴度，dpε是等效塑性应变增量，η是表示临界空穴扩张比的材料参数，为材料的固有属性，对于一种指定的材料η为常量，其值随着材料韧性的增加而增大．η的取值可以通过圆周平滑槽口试件单向拉伸试验来校准．

上述VGM判据包含了应力三轴度对塑性应变的显式积分．然而在许多实际情况下，应力三轴度在加载历史中几乎保持不变，因此，式(1)中积分号内的项可以提出作为乘积，从而得到SMCS判据：

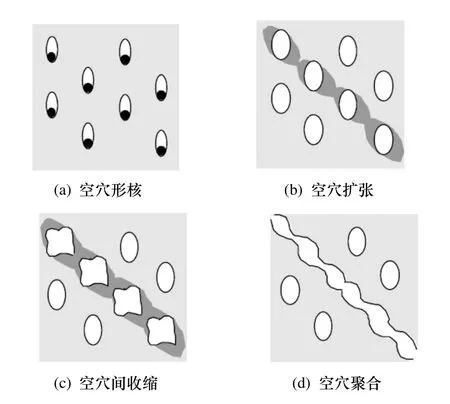
图1 空穴形核，扩张和聚合机理Fig.1 Void nucleation, growth and coalescence mechanism

其中韧性参数α与VGM模型中的参数η类似，是一个材料常数，可以通过圆周平滑槽口试件单向拉伸试验来校准．在上述微观断裂判据中，延性裂纹开展是整体行为，而不是单个材料点的行为，因此还需要定义一个包含若干材料点的特征长度参数l*，微观断裂判据必须在特征长度l*上得到满足才能引发断裂．l*的大小取决于材料的微观结构，可由材料拉伸试件的断口扫描电镜试验得到．目前建议使用的l*取两个界限值和平均值[7]，下限取材料平均波纹直径的两倍，上限取观察电子照片得到的最大凸起或凹陷部分的长度，l*的平均值取大约10个凸起或凹陷长度的平均值．

2 试验概况

2.1 节点焊接及试件制作

为了校准以上微观机制模型中的参数，本次试验设计了Q460钢母材及ER55-G型焊材的轴对称平滑圆棒拉伸试验和圆周平滑槽口圆棒拉伸试验，试验中各试件编号如表1所示．

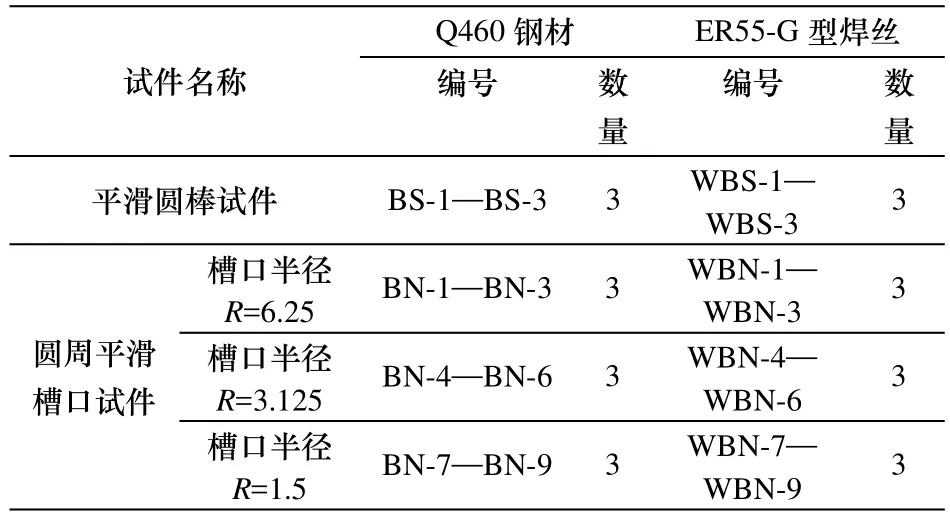
表1 试件编号表Tab.1 Number of the specimens

本试验所研究的 Q460D低合金高强度结构钢由上海宝山钢铁有限公司提供．试验中所有母材试件均从厚度为36 mm的Q460D热轧型高强钢板上抽取加工而成．表2列出了本批Q460D高强钢材的化学成分含量．根据出厂报告显示，本批Q460D钢材的名义屈服应力为488 MPa，名义极限应力为618 MPa，钢材伸长率为23%，屈强比为0.79，符合《低合金高强度结构钢》（GB/T1591-2008）中的技术要求．

表2 Q460D钢材化学成分含量/%Tab.2 Chemical composition of Q460D steel (in wt/%)

本次试验中的焊材试件分别从几块预制好的焊接钢板试件上抽取、加工而成(见图2）．

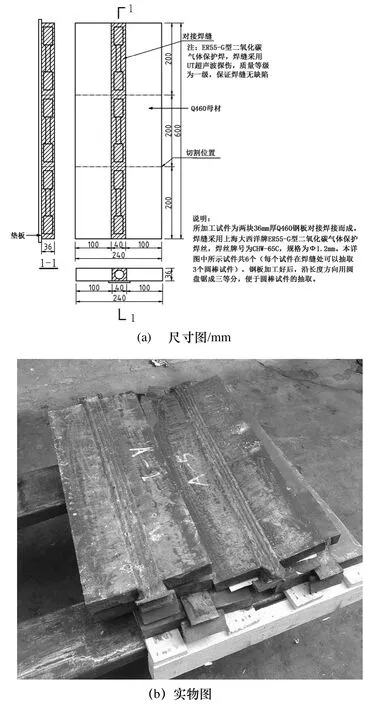
图2 用于加工圆棒试件的焊接钢板Fig.2 Welding steel plate used for machining round bar specimen

所有焊接钢板试件均为两块36mm厚的Q460D钢板对接焊接而成．钢板焊缝处采用上海大西洋牌ER55-G型二氧化碳气体保护焊丝，焊丝牌号为CHW-65C，规格为Ф1.2 mm．试件焊接时，焊缝部位下端设有垫板．试件焊好后，采用UT超声波技术对焊缝部位进行探伤，保证焊接质量等级为一级．根据出厂报告显示，本次试验中所采用的上海大西洋牌ER55-G型焊丝实测屈服应力为670 MPa，极限应力为760 MPa，伸长率为21%，-20℃标准夏比标准试件平均V型冲击功为100 J，符合《气体保护电弧焊用碳钢、低合金钢焊丝》（GB/T8110-1995）中的要求．

2.2 单轴拉伸试验

从图2所示的钢板焊接连接件中抽取并制作母材和熔敷金属平滑圆棒试件各3个，共6个进行单轴拉伸试验，试件设计尺寸如图3所示，试件编号及标距段直径分别见表3和表4．试验在西安交通大学航空航天学院力学试验室完成．试验加载设备采用MTS-880型电子万能试验机，试验机最大拉力为200 kN．试验中，圆棒的轴向应变采用MTS电子应变引伸计测量，引伸计标距长度为20 mm，延伸率为25%．试验加载采用位移控制，试验机与引伸计上的数据采集频率为20 Hz，可获得母材和熔敷金属的全应力应变曲线．

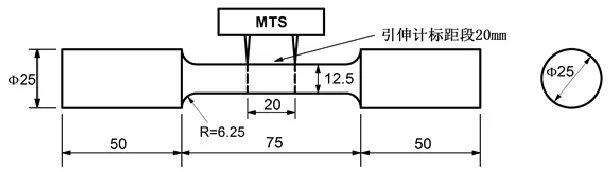
图3 平滑圆形拉伸试件Fig.3 Smooth round tensile specimen

单轴拉伸试验所得的各母材和熔敷金属试件的屈服强度σy、极限强度σu、弹性模量E结果列于表3．

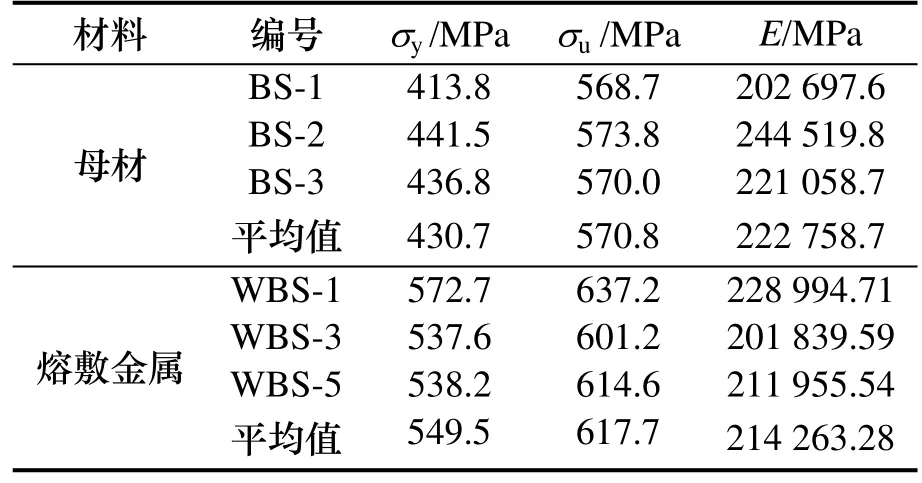
表3 单轴拉伸试验结果Tab.3 Uniaxial tensile test results

上述两种材料根据试验数据得到的应力应变曲线均只到摘引伸计前，实际上材料在摘引伸计后到断裂发生前还能发生很大的变形，在ABAQUS有限元模型中用到的材料真实应力-塑性应变曲线应延伸到断裂时刻．为此，需要测量单轴拉伸试件断后的直径和断裂时所能承受的力，按下式(3)、(4)计算断裂时刻的真实应力和应变，计算结果见表4．

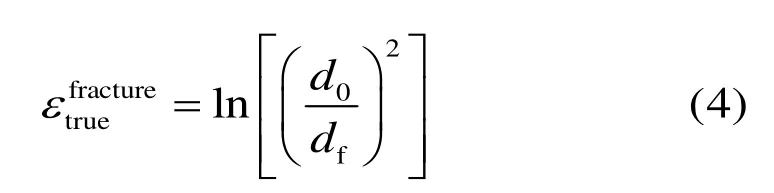
式中：d0是试件标距段的初始直径，df是试验结束后测得的试件标距段的断裂直径．三种材料的真实应力-塑性应变曲线应由摘引伸计前的试验曲线延伸到断裂点，如图4所示．在后续的圆周平滑槽口单向拉伸和反复加载试验试件的ABAQUS有限元分析中，材料属性均按图4中的曲线输入关键点．

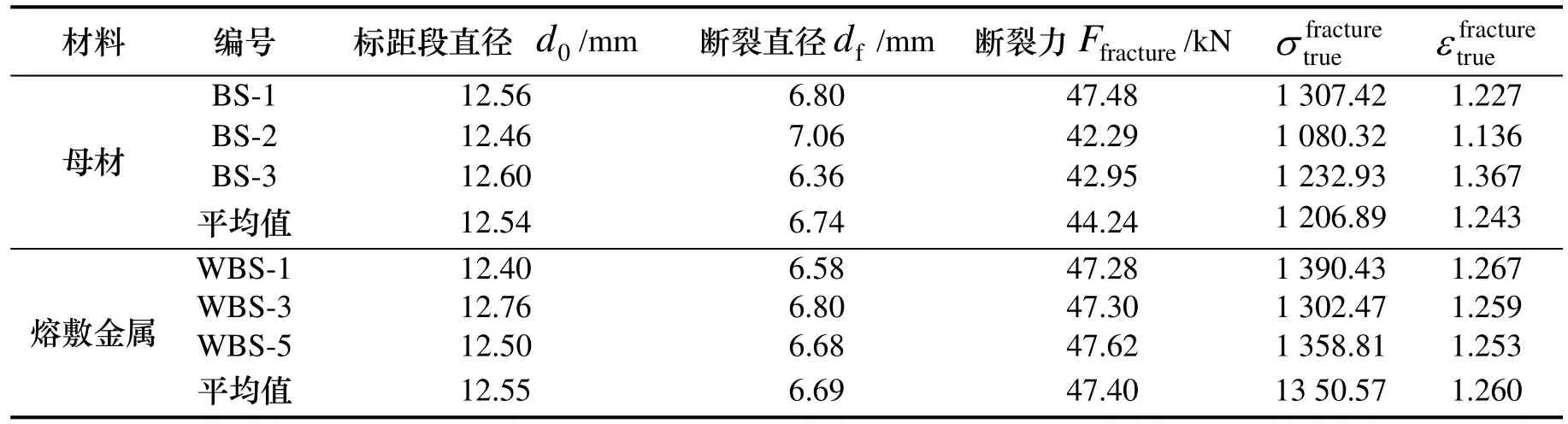
表4 单轴拉伸试件断裂时的真实应力和应变Tab.4 The true stress and strain of uniaxial tension specimen

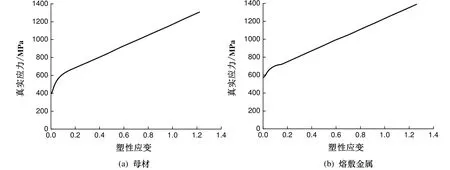
图4 真实应力-塑性应变曲线Fig.4 True stress-strain curve.

2.3 圆周平滑槽口试件单向拉伸试验

从图2所示的钢板焊接连接件中抽取并制作母材和熔敷金属两种材料的圆周平滑槽口试件，每种材料取三种不同的槽口半径R=1.5 mm，3.125 mm和6.25 mm，以提供三种不同的应力三轴度，每种形式的试件制作3个，共18个试件．试件设计尺寸如图5所示，试件编号及实测尺寸见表5．试验在西安交通大学航空航天学院力学试验室进行，引伸计和加载装置与单轴拉伸试件相同．

图5 圆周平滑槽口试件Fig.5 Smooth notched round bar specimen

对母材和熔敷金属两种材料制成的圆周平滑槽口试件进行单轴拉伸试验，得到的典型母材试件力-变形（标距段）曲线，曲线下降段的斜率突变点为延性裂纹开展的点，它对应的断裂伸长量fΔ可以作为有限元分析中的控制变形来反算断裂参数α和η．

用有限元软件ABAQUS考虑非线性和大变形的塑性模型来模拟每一个开槽口拉伸试件．采用二维轴对称有限元模型，选取8节点四边形双二次轴对称减缩积分单元CAX8R，在开槽区域单元尺寸为0.25 mm（如图6所示）．由图7可见试件危险截面的中心附近应力应变梯度很缓，SMCS和VGM任一断裂判据在危险截面中间大部分区域几乎同时得到满足，所以可以认为试件整个危险截面几乎同时发生断裂，即断裂破坏主要取决于断裂韧性参数α和η，而与特征长度参数*l关系不大，因此圆周平滑槽口试件单向拉伸试验适合于校准参数α和η．图8给出了母材三种开槽尺寸试件的试验和有限元分析得到的力-变形曲线，可以看出试验曲线与有限元分析曲线吻合较好，其余试件力-变形曲线与此也有类似结果．

SMCS模型参数α的值可以由开不同半径槽口的拉伸试件的试验和分析确定．拉伸试验确定了断裂开始时的变形fΔ．对每一种几何尺寸的开槽口拉伸试件进行有限元分析，得到对应于变形fΔ的应力和应变．将这些横截面的临界应力和应变状态代入SMCS判据，并令截面中点处的SMCS值为0，即令式（2）等于0，得到式（5）以确定断裂参数α, 计算结果见表5．

VGM模型的参数η的校准过程与SMCS模型的参数α校准过程类似，只是数学表达式稍微不同．η可以由式（6）在破坏点的值来计算．与SMCS校准一样，VGM校准也是基于断裂开始的试验位移fΔ．有限元分析中足够多的增量步保证了计算式(6)等式右边积分的精确性，参数η计算结果见表5．

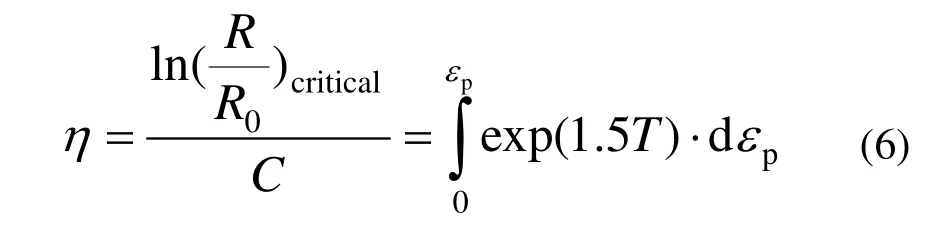
图6 圆周平滑槽口单向拉伸试件二维轴对称有限元模型（R=1.5 mm）Fig.6 The two-dimensional axisymmetric finite element model of smooth notched round bar uniaxial tensile specimens (R=1.5 mm)

图7 开槽区域的应力应变场（试件BN-9）Fig.7 Stress and strain field in the slot region

图8 典型圆周平滑槽口试件单向拉伸试验和有限元力-变形曲线Fig.8 Test and finite element force - deformation curves of typical smooth notched round bar tensile specimens

表5 参数α和η计算结果Tab.5 The calculation results ofαandη

由表5计算结果可以看出：试件槽口半径越大，临界等效塑性应变越大，而应力三轴度越小，不同开槽尺寸试件得到的α值和η值很接近，表明α和η是表征材料断裂韧性的基本参数．母材和熔敷金属的α和η值较为接近．（BN-2试件由于加工过程中出现问题，导致槽口宽度偏大，所得出来的参数参考价值有限）．校准的两种材料的微观机制模型参数可以用于预测Q460钢焊接节点的开裂位置和时刻．

2.4 扫描电镜试验

对Q460钢母材和熔敷金属两种材料圆周平滑槽口单向拉伸试验拉断的6个试件进行断口扫描电镜试验，以测得两种材料的特征长度l*．Q460钢母材试件断口电镜扫描在西安交通大学机械制造系统工程国家重点实验室完成，观测设备采用日立SU8010型高分辨率场发射扫描电子显微镜，二次电子分辨率为1 nm．ER55-G型焊材试件断口电镜扫描试验在长安大学材料与工程学院实验室完成，观测设备采用日立SU4800型场发射扫描电子显微镜，二次电子分辨率为1.4 nm．

通过扫描电镜试验，得到典型断裂表面如图9所示．对两种材料特征长度l*取两个界限值和一个平均值，表6列出了每个试件特征长度的上限、平均值和下限，两种材料的特征长度平均值在0.085～0.143 mm范围内．

图9 圆周平滑槽口试件断口电镜图Fig.9 Fracture electron figures of notched round bar specimen

3 校准的Q460钢参数与其他结构钢参数的比较

Kanvinde和 Deierlein已经校准了四种美国结构用钢和三种日本结构用钢的单调加载微观机制模型参数[3]．廖芳芳校准了 Q345钢母材、熔敷金属和热影响区三种材料的微观机制模型参数[10]．本节将校准的国产高强度Q460钢母材和熔敷金属两种不同部位材料微观机制模型参数与之前校准的这十种结构钢参数进行比较，结果如表7所示．结果表明：SMCS模型中的韧性参数α和VGM模型中的韧性参数η与材料的延性有关，材料的延性定义为单轴拉伸试件标距段的初始直径与拉断直径的比值普遍情况下材料延性越大，α和η的值也越大，而α和η的值与材料的屈服强度、极限强度和强屈比关系不大，特征长度参数l*与材料特性无关．

表6 各试件测得的特征长度Tab.6 Characteristic length of each specimen

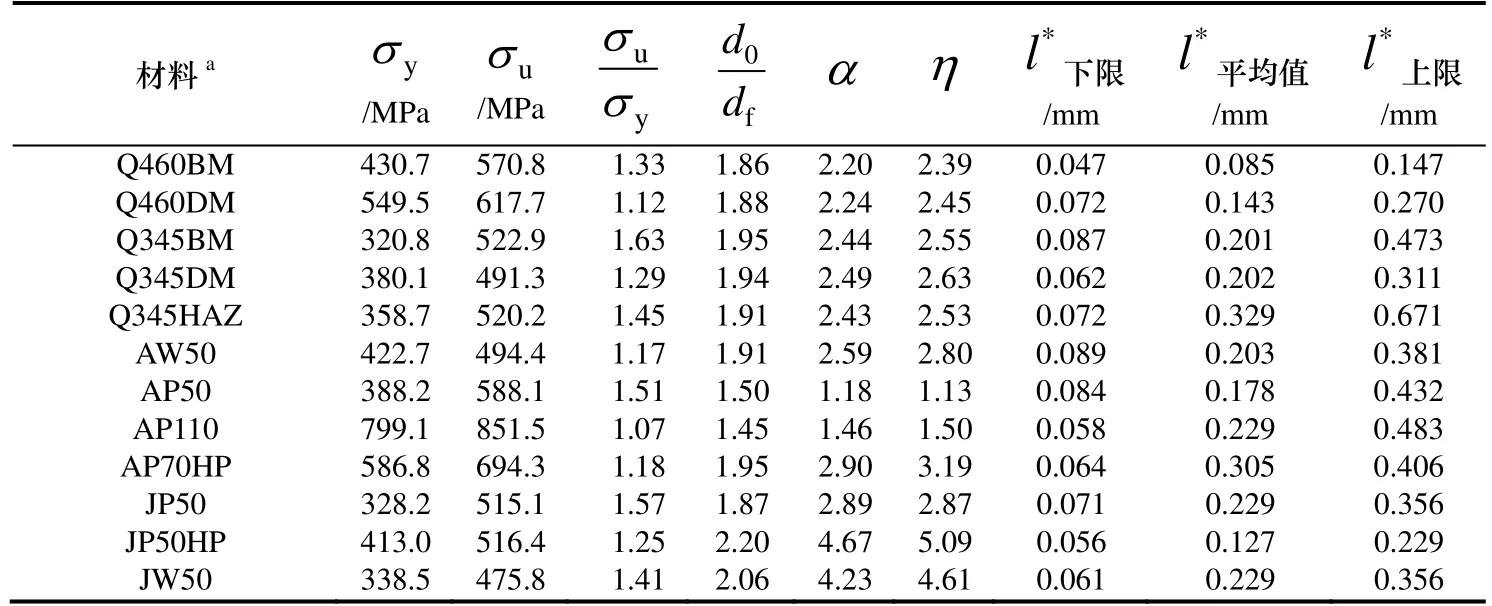
表7 不同结构钢单调加载微观机制模型参数对比Tab.7 Comparison of the parameters of the model parameters of the monotonic loading of different structural steels

4 有限元分析裂后路径及其与试验结果的对比

有限元方法是处理开裂等强非线性不连续力学过程的最主要分析方法．现行通用有限元软件在处理工程问题中各有特点，其中ABAQUS对于处理开裂等强非线性过程有着独特的优势．

目前，ABAQUS分析材料或结构开裂的主要方法分为两类，分别基于断裂力学理论和损伤力学理论．基于断裂力学的分析方法通过计算裂纹尖端应力强度因子或J积分等判据判断开裂，而基于损伤力学方法的模型则通过材料损伤导致刚度不断折减，最后形成断裂带．分析裂纹扩展的方法主要包括虚拟裂纹闭合法（VCCT）、粘聚力模型(Cohensive)和扩展有限元法(XFEM)．常规有限元法(CFEM)(包括虚拟裂纹闭合法和粘聚力模型分析)采用连续函数作为插值函数，因此建模时裂纹只能与单元边重合，裂纹尖端设置在节点上，限制了裂缝的发展速度和开裂方向，单元划分对计算结果影响较大．同时，裂纹扩展过程中，有限元程序需要根据裂纹扩展不断重新划分网格，计算代价巨大．扩展有限元法(XFEM)所使用的网格与结构内部几何及物理参数无关，因此在处理连续开裂问题时较为有效，但是它使用的断裂判据没有考虑应力三轴度对断裂应变的影响，无法适用于以三向应力状态为主的断裂问题，对于三维有限元分析断裂问题也不够准确，且对于大应变问题经常不收敛，所以也有很大的局限性．

本文采用自编的ABAQUS子程序VUMAT，以校准的单调荷载作用下的SMCS和VGM模型为断裂判据，将分析过程中判定失效的单元逐个删除，得到开裂后的荷载位移曲线和裂缝发展路径，从而提供一种可用于延性断裂后路径跟踪分析的有限元方法．

有限元软件ABAQUS子程序UMAT适合隐式标准分析，但是在分析裂后路径时需要迭代刚度矩阵，经常不收敛，因此，编写了适合显式动力分析的VUMAT子程序模拟单调荷载作用下的圆周平滑槽口试件的裂后路径，在加载速率很小的情况下，显式分析结果与隐式差别不大．

用户子程序VUMAT用来定义材料的力学本构关系，可以被用户子程序定义材料计算点调用，可以使用和更新结果依赖状态变量，可以使用传入的任何场变量．满足用户定义的破坏准则的材料点可以从模型中删除．当用户给结果依赖状态变量分配空间时，用户需要指定控制单元删除标示的状态变量号．在VUMAT中删除状态变量可以被赋予1或者0．1表示材料点是激活的，0表ABAQUS/Explicit将通过设定应力为0从模型中删除材料点．在分析过程中传递给用户子程VUMAT的材料点结构保持不变；删除的材料点没有从块中移走．ABAQUS/Explicit将传递0应力及应变给所有删除的材料点．一旦一个材料点被标示为删除，该材料点将不能够被再次激活．

用自编的VUMAT子程序，分别以SMCS和VGM模型为断裂判据，分析了圆周平滑槽口单向拉伸试件的开裂全过程，得到了裂后荷载位移曲线，并将其与试验结果进行了对比．

有限元模型单元尺寸划分如图6所示，但用VUMAT子程序进行显式动力分析时，单元类型只能选取线性CAX4R单元．图10和11分别给出了典型试件BN-6以SMCS和VGM为断裂判据在不同变形下的应力云图，随着变形的增加，试件中间危险截面满足断裂判据的单元被逐个删除，可以得到裂缝开裂的全过程，其余试件不同变形下的应力云图与此类似．比较图10和11可以看出，以VGM模型为断裂判据，在加载过程中，试件中间危险截面单元删除比以SMCS模型为断裂判据更整齐．

典型母材试件裂后荷载位移曲线与试验结果的对比见图12．

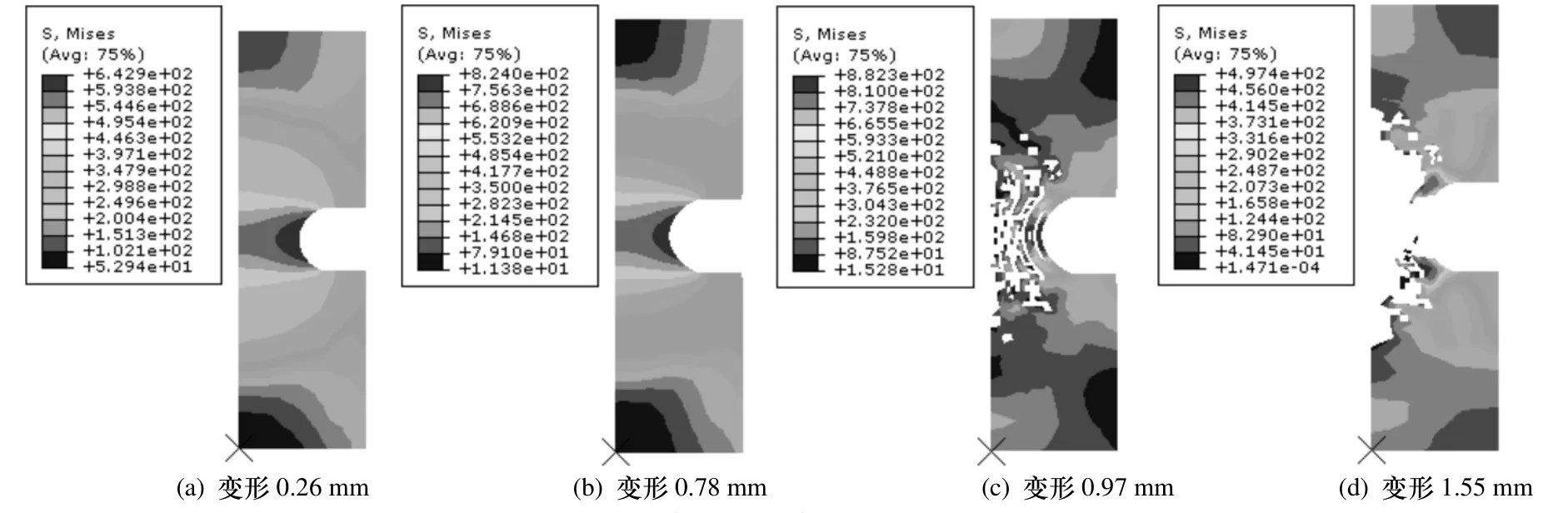
图10 试件BN-7不同变形下的应力云图（SMCS为断裂判据）Fig.10 Stress cloud images under different deformation of specimen BN-7(SMCS as the fracture criterion）

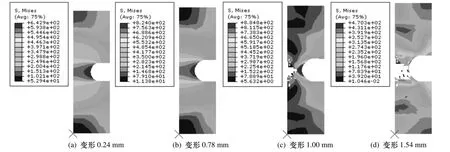
图11 试件BN-7不同变形下的应力云图（VGM为断裂判据）Fig.11 Stress cloud images under different deformation of specimen BN-7(VGM as the fracture criterion）

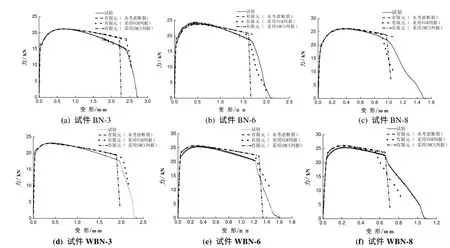
图12 圆周平滑槽口单向拉伸试件用VUMAT子程序模拟开裂荷载位移曲线与试验曲线对比Fig.12 Comparison of the cracking load displacement curves simulated by VUMAT subroutine and test curves for smooth notched round bar uniaxial tensile specimens

由图12可以看出，没有用VUMAT子程序的有限元分析得不到荷载位移曲线的斜率突变点；用自编的VUMAT子程序，将失效的单元逐个删除，可以得到圆周平滑槽口单向拉伸试件开裂后的荷载位移曲线下降段，与试验曲线比较接近，曲线斜率突变点对应的开裂时刻与试验开裂时刻稍有差别是因为校准的SMCS和VGM模型的断裂韧性参数α和η取的是平均值，个别试件会稍有差别，例如试件BN-8，由表5可知，其断裂时刻对应的α和η值分别为2.23和2.43，大于母材α和η的平均值2.20和2.39，而有限元分析中用的是平均值，因此判断的开裂时刻要早于试验结果，其他试件与此类似，表5中α和η值与平均值相差越大的试件，在图12中曲线开裂时刻对应的斜率突变点与试验结果相差越大．另外，用VUMAT子程序进行显式动力分析时，单元类型只能选为线性CAX4R单元，与第4章校准参数α和η时选用的二次单元CAX8R分析出来的单元应力会稍有误差，这也会导致曲线斜率突变点与试验结果的差别．

5 结论

进行了Q460钢母材和熔敷金属两种材料的6个单轴拉伸试验，18个圆周平滑槽口试件单向拉伸试验和有限元分析，6个断口扫描电镜试验，校准了两种材料的微观机制模型SMCS和VGM模型的断裂韧性参数和特征长度参数，用自编的VUMAT子程序，分别以校准的SMCS和VGM模型为断裂判据，分析了18个圆周平滑槽口单向拉伸试件的开裂全过程，得到了裂后荷载位移曲线，并将其与试验结果进行了对比，得到以下结论：

（1）Q460钢母材和熔敷金属的断裂韧性参数较为接近．

（2）SMCS和VGM模型中的断裂韧性参数与材料的延性有关，材料延性越大，断裂韧性参数的值也越大，而断裂韧性参数与材料的屈服强度、极限强度和强屈比关系不大，特征长度参数与材料特性无关；Q345钢母材、熔敷金属和热影响区三种材料的延性分别明显高于Q460钢的母材和熔敷金属，且其α和η值也明显大于Q460钢．

（3）用自编的VUMAT子程序，分别以SMCS和VGM模型为断裂判据，可以得到圆周平滑槽口试件在单调拉伸荷载作用下的裂后荷载位移曲线下降段，与试验曲线比较接近，曲线下降段斜率突变点对应的断裂荷载与试验值也比较接近．验证了在有限元分析中引入微观机制断裂判据得到钢结构焊接节点全程荷载位移曲线的可行性．

（4）在用自编的VUMAT子程序时，以VGM模型为断裂判据删除失效单元更整齐，预测的裂后路径也更准确，因此推荐用VGM断裂判据．

References

[1] KUWAMURA H, AKIYAMA H. Brittle fracture under repeated high stresses [J]. Journal of Constructional Steel Research, 1994, 29 (1-3): 5-19.

[2] TATEISHI K, HANJI T, MINAMI K. A prediction model for extremely low cycle fatigue strength of structural steel[J]. International Journal of Fatigue, 2007, 29(6):887-896.

[3] KANVINDE A M, DEIERLEIN G G. Micromechanical simulation of earthquake-induced fracture in steel structures. Technical Rep. 145, John A. Blume Earthquake Engineering Center, Stanford University, Calif, 2004.

[4] HANCOCK J W, MACKENZIE A C. On the mechanics of ductile failure in high-strength steel subjected to multi-axial stress states [J]. Journal of the Mechanics and Physics of Solids, 1976, 24(3): 147–169.

[5] RICE J R, TRACEY D M. On the ductile enlargement of voids in triaxial stress fields [J]. Journal of the Mechanics and Physics of Solids, 1969, 17(3): 201–217.

[6] KANVINDE A M, DEIERLEIN G G. Prediction of Ductile Fracture in Steel Moment Connections During Earthquakes Using Micromechanical Fracture Models.13th World Conference on Earthquake Engineering, Vancouver, B.C., Canada, Paper No. 297, 2004.

[7] KANVINDE A M, DEIERLEIN G G. Void Growth Model and Stress Modified Critical Strain Model to Predict Ductile Fracture in Structural Steels [J]. Journal of Structural Engeering, ASCE, 2006, 132(12): 1907-1918.

[8] KANVINDE A M, DEIERLEIN G G. Finite-Element Simulation of Ductile Fracture in Reduced Section Pull-Plates Using Micromechanics-Based Fracture Models[J]. Journal of Structural Engeering, ASCE, 2007, 133(5):656–664.

[9] KANVINDE A M, FELL B V, GOMEZ I R, et al. Predicting fracture in structural fillet welds using traditional and micromechanical fracture models ［J］. Engineering Structures, 30(2008): 3325-3335.

[10] LIAO F F, WANG W, CHEN Y Y. Parameter calibrations and application of micromechanical fracture models of structural steels [J]. Structural Engineering and Mechanics,2012, 42(2): 153-174.