OFDM系统中基于盲检测的低复杂度分块SLM算法

杨　霖, 何向东, 刘雲雲

(电子科技大学通信抗干扰技术国家级重点实验室, 四川 成都 611731)



OFDM系统中基于盲检测的低复杂度分块SLM算法

杨霖, 何向东, 刘雲雲

(电子科技大学通信抗干扰技术国家级重点实验室, 四川 成都 611731)

摘要：为了降低正交频分复用(orthogonal frequency division multiplexing, OFDM)系统中传统选择性映射(conventional selected mapping, CSLM)算法的计算复杂度,提高系统的频谱利用效率,提出了一种基于盲检测的低复杂度分块选择性映射(block selected mapping, BSLM)算法,发送端利用逆快速傅里叶反变换(inverse fast fourier transform,IFFT)性质仅需少量低维IFFT运算即可获得较多的备选序列,接收端采用低复杂度的盲检测方式。仿真分析了所提算法的峰均功率比(peak to average power ratio, PAPR)、立方度量(cubic metric, CM)和误比特率(bit error rate, BER)性能。结果表明,所提算法不仅明显降低了计算复杂度,而且有效抑制了OFDM信号的PAPR和CM,获得与已知边带信息的CSLM算法相近的BER性能。

关键词：正交频分复用; 峰均比; 立方度量; 选择性映射; 盲检测

0引言

正交频分复用(orthogonal frequency division multiplexing, OFDM)技术是通信领域的研究热点,它凭借强大的抗衰落能力和高效的数据传输速率被当前许多热点通信业务所采用。然而,该技术主要缺点之一是OFDM信号具有较高的峰均功率比(peak to average power ratio, PAPR),要求功率放大器(high power amplifier, HPA)具有较高的线性范围,导致HPA的功率效率降低。另外,功率放大器的非线性会使动态范围大的信号产生非线性失真,降低系统的误比特率(bit error ratio, BER)性能[1]。目前,抑制OFDM信号的PAPR已有许多成果。例如:限幅方式[2]、压扩算法[3-4],这两种算法复杂度较低,但算法本身会引入非线性干扰或扩大噪声功率从而使得系统BER性能恶化;概率类算法:部分传输序(partial transmit sequence, PTS)[5-6]、选择性映射(selected mapping, SLM)[7-8]以其良好的PAPR抑制能力而备受关注。然而,传统选择性映射(conventional selected mapping, CSLM)中,获得不同的备选序列需要进行多次逆快速傅里叶反变换(inverse fast fourier transform, IFFT),导致计算复杂度较高,并且需要发送端传送额外的边带信息来恢复原始信号。为了降低复杂度,许多改进的SLM算法[9-13]被提出,其中文献[10-11]中提出了利用时域信号循环移位方式减少了IFFT运算次数,一定程度上降低了发送端的计算复杂度。文献[12-13]中均使用了分块和重组的思想,文献[12]中提出了广泛线性选择性映射(widely linear selected mapping, WSLM)算法,该算法先将原始频域序列分成实部和虚部子块序列,然后对实部和虚部子块分别进行SLM算法并进行组合,发送端采用线性信号处理技术降低了算法的复杂度。文献[13]中提出了一种分块选择性映射(block selected mapping, BSLM)算法,将原始序列分割成多个子块,对每个子块乘上相位序列后单独进行IFFT运算获得到时域子块信号,并对时域子块重新组合来获得多个时域备选信号,有效降低了信号的PAPR,在一定程度上降低了发送端的计算复杂度。然而,文献[12-13]中的算法发送端的计算复杂度仍然较高,且需要传送额外的边带信息来恢复原始信号。文献[14]利用相位因子序列循环移位和时域信号变换,通过少量IFFT获得良好的PAPR抑制性能,但其大大增加了接收端的复杂度。为了进一步降低发送端和接收端的复杂度,提高频谱利用效率,本文基于IFFT运算性质和分块组合的思想,提出了改进的分块选择性映射(modified block selected mapping, MBSLM)算法,通过少量低维IFFT运算即可获得较多的备选序列,接收端采用低复杂度的盲检测方式,不需要发送端传送额外的边带信息。同时本文仿真分析了CSLM、WSLM、BSLM、MBSLM算法的PAPR和BER性能。结果表明,所提算法有效降低了发送端和接收端的计算复杂度,获得了良好的PAPR抑制性能,接收端采用低复杂度的盲检测方式能够获得与已知边带信息的CSLM算法、WSLM算法相近的BER性能。

1OFDM技术简介

1.1OFDM信号产生及度量

OFDM信号是通过不同载波调制的信号叠加获得的,原始频域信号表示为:X=[X(0),X(1),…,X(N-1)],其中N表示子载波数,频域信号通过IFFT调制后获得时域信号x:

(1)

OFDM信号的PAPR定义为

(2)

式中,|·|2表示求瞬时功率；max[·]表示求最大值；E[·]表示求平均值。

另外,在3GPP中还采用了另一种度量OFDM信号包络波动的方式,即立方度量(cubic metric, CM)[15],定义如下:

(3)

式中,RCMref和K 均为常量,原始立方度量(raw cubic metric, RCM)定义为

(4)

使用互补累积分布函数(complementary cumulative distribution function,CCDF)来表示PAPR或RCM超过某个给定值的概率,例如:

(5)

1.2固态放大器模型

发送端的功率放大器会使OFDM信号产生严重的非线性失真,影响系统的BER性能。固态功率放大器(solidstatepoweramplifier,SSPA)是通信系统中常用的放大器之一,Rapp模型[16]常被用来模拟SSPA放大器的非线性特征,在该模型中,输入信号x的采样点极坐标形式为x(n)=|x(n)|ejθ(x(n)),HPA的输出信号y的采样点表示为

(6)

式中,|·|表示求幅度；θ(·)表示求相位；A(·)表示放大器的幅度响应AM/AM；φ(·)表示放大器的相位响应AM/PM。放大器的非线性特征表示为

(7)

式中,p表示放大器的平滑因子;A0表示放大器的最大输出,由放大器的输入饱和点Asat唯一确定,Asat由输入回馈(inputback-off,IBO)决定,即

(8)

式中，pin表示输入信号的平均功率。

2MBSLM算法基本原理

2.1CSLM算法

CSLM算法是将原始频域序列X分别乘上不同的相位因子序列,经过多次IFFT调制获得时域备选序列,相位旋转因子序列表示为:P=(P1,P2,…,PU),其中U表示相位旋转序列个数。原始频域信号X与相位旋转序列Pu(1≤u≤U)相乘后获得频域备选信号Xu,频域信号经过IFFT调制后得到多个独立的时域备选序列xu=[xu(0),xu(1),xu(N-1)],并从时域备选序列中选出PAPR最小的信号进行传输。

2.2WSLM算法

图1　WSLM算法的原理框图

2.3BSLM算法

BSLM算法是将原始频域序列X分割成V个频域子序列,将每个频域子序列乘上U个不同的相位旋转序列,通过IFFT运算获得U个不同的时域子序列组成对应的时域子序列集合。最后从每个时域子序列集合中任取一个,将所取得的V个时域子序列相加获得时域备选信号,并从时域备选信号中选择出PAPR最小的信号进行传输,如图2所示。

2.4MBSLM算法

虽然WSLM算法和BSLM算法在一定程度上降低了发送端的复杂度,但复杂度仍然较高,且需要传送额外的边带信息,降低了频谱利用效率。为了进一步降低发送端的计算复杂度,提高频谱利用效率,本文结合IFFT运算性质,提出MBSLM算法,发送端仅需要少量低维IFFT运算,接收端采用低复杂度的盲检测方式,不需要发送端传送额外的边带信息。

图2　BSLM算法的原理框图

2.4.1IFFT运算性质

性质 1给定频域序列的长度为NV,其中含有S个非零元素,相邻的两个非零元素之间有T-1个0元素。具体形式如下:

(9)

通过IFFT获得的时域序列可以表示为

(10)

式中，X′=[X0,X1,…,XS-1]。

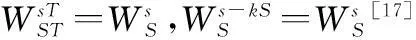
(11)

证毕

性质 2[17]频域信号循环移位对应时域信号乘上相位旋转因子,即

IFFT (X(m))=IFFT (X)·Wm

(12)

2.4.2MBSLM算法的发送端

MBSLM算法发送端处理过程如图3所示。

(1) 将频域序列X交织分割为V个频域子序列,令f1=[1,0,0,0,…,1,0,0,0],fv表示f1向右循环移动v-1(v=2,…,V)位,子块序列表示为

Xv=fv·X

(13)

(14)

(15)

(16)

(17)

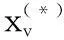
图3　MBSLM算法发送端的原理框图

2.4.3MBSLM算法的接收端

在接收端,传统的盲检测方式[18]需要将相位序列集合中的所有相位因子序列分别与接收到的频域信号相乘,通过判断各频点与最近星座点最小距离总和来选择出最有可能的相位因子序列,将接收到的时域信号通过快速傅里叶变换(fastFouriertransform,FFT)运算后获得频域信号Y,采用如下准则判断最有可能的相位因子序列:

(18)

式中,()*表示求共轭；η表示相位因子序列集合；δ表示已知星座点集合；H表示信道响应。

根据式(18)可知,对于传统的盲检测方式,算法的计算复杂度随着备选序列个数的增加而线性增加,当备选序列个数较大时,整个接收端算法的复杂度也较大。

为了降低盲检测的复杂度,本文结合MBSLM算法的分块特点,提出了低复杂度的盲检测方式,接收端具体处理过程如图4所示。

图4　MBSLM算法接收端盲检测原始框图

(1) 接收的时域信号y进行FFT运算后获得频域信号Y。

(2) 将每个子载波的信号乘上备选相位因子,并通过与最近星座点的距离来判断出单独最优的相位因子,记作

(19)

(3) 将步骤2中优选出的单独最优的相位因子集合P交织分割成V个相位序列子块Pv(1≤v≤V)。

(5) 将二次优选出的相位序列子块相加获得最优的相位序列

(20)

(6) 将选出的最优相位序列与频域信号Y共轭相乘,即可恢复出原始频域信号

(21)

3计算复杂度分析

3.1发送端的复杂度

为了衡量计算复杂度降低程度,本文使用计算复杂度降低比(computationalcomplexityreductionratio,CCRR),其定义为

(22)

表1和表2给出了当子载波数为256时,当产生相同个数的时域备选序列时,CSLMWSLM、BSLM和MBSLM算法所需的复数加法和复数乘法次数,其中CCRR1、CCRR2、CCRR3分别表示MBSLM算法相对于CSLM、WSLM和BSLM算法的复杂度降低比值。

表1　时域备选序列数为16时发送端的复杂度比较

表2　时域备选序列数为81时发送端的复杂度比较

由表1可知,当备选序列数为16时,MBSLM算法相对于CSLM算法,复数乘法和复数加法次数对应的CCRR1分别达到81.3%和65.6%;相对于WSLM算法,复数乘法和复数加法次数对应的CCRR2分别为62.5%和45.0%;相对于BSLM算法,复数乘法和复数加法次数对应的CCRR3分别达到了62.5%和51.4%。由表2可知,当备选序列数为81时,MBSLM算法相对于CSLM算法,复数乘法和复数加法次数对应的CCRR1分别达到94.4%和73.1%;相对于WSLM算法,复数乘法和复数加法次数对应的CCRR2分别为75.0%和22.6%;相对于BSLM算法,复数乘法和复数加法次数对应的CCRR3分别达到了62.5%和32.5%。因此,MBSLM算法相比于CSLM算法、WSLM算法和BSLM算法均明显降低了发送端的计算复杂度。

3.2接收端的复杂度

表3给出了当子载波数N为256,调制方式为正交幅度调制(quaternary amplitude modulation, QAM),调制阶数为16,即星座点集合元素个数为M=16,相位因子集合元素个数L=2,当时域备选序列个数K相同时,传统的盲检测和改进的盲检测方式所需的复数乘法和复数加法次数以及CCRR值。

表3　传统盲检测方式和改进盲检测方式的复杂度比较

由表3可知,改进的盲检测方式相比于传统盲检测方式,当备选序列为16时,所需复数乘法和复数加法次数对应的CCRR分别达到了87.5%和87.4%,当备选序列为81时,所需复数乘法和复数加法次数对应的CCRR分别达到了97.5%和97.5%。因此,本文提出的改进盲检测算法不需要发送端传送额外的边带信息,提高了频谱利用效率,相比于传统盲检测算法明显降低了计算复杂度,随着备选序列的增多,计算复杂度降低程度增强。

4仿真结果与分析

本文仿真分析了CSLM、WSLM、BSLM和MBSLM算法的PAPR和RCM性能,以及在信道1和信道2下的BER性能。信道1:AWGN信道;信道2:EVA70信道。扩展ITU信道主要包括EPA5、EVA70和ETU300三种,分别代表低时延、中时延和高时延扩展信道,并且多普勒频移分别为5 Hz、70 Hz和300 Hz。本文选择中时延的EVA70信道作为仿真信道模型。仿真参数和信道参数如表4和表5所示。

表4　仿真参数表

表5　信道模型的功率延迟参数(信道2:扩展车载A(EVA))

4.1PAPR和RCM性能分析

图5中给出了CSLM、BSLM和MBSLM算法的PAPR性能曲线。由图可知,CSLM算法、WSLM、BSLM和MBSLM算法均能有效降低OFDM信号的PAPR。在CCDF=0.1%处,原始信号对应的PAPR0为10.90 dB,当备选序列数为16时,CSLM、WSLM、BSLM和MBSLM算法对应的PAPR0分别为7.45 dB、7.55 dB、7.70 dB和7.70 dB,其相对于原始信号的PAPR0分别降低了3.45 dB、3.35 dB、3.20 dB和3.20 dB,MBSLM算法与BSLM算法的性能相当,而比CSLM和WSLM算法分别差0.25 dB和0.15 dB;但备选序列数增加到81时,CSLM、WSLM、BSLM和MBSLM算法对应的PAPR0更是下降到6.80 dB、6.85 dB、6.90 dB和6.90 dB,MBSLM算法仍然与BSLM算法性能相当,却仅比CSLM算法和WSLM算法分别差0.10 dB和0.05 dB。因此,一方面本文提出的MBSLM算法能够获得与BSLM算法一致的PAPR抑制性能,但由表1可知,MBSLM算法发送端的计算复杂度明显低于BSLM算法;另一方面虽然MBSLM算法的PAPR抑制性能稍微不如CSLM算法和WSLM算法,但由表1可知,MBSLM算法发送端的计算复杂度远比CSLM算法和WSLM算法的计算复杂度低。

图5　各种算法的PAPR性能曲线

图6中给出了各种算法的RCM性能曲线。由图可知,CSLM、BSLM和MBSLM算法均能有效降低OFDM信号的RCM。在CCDF=0.1%处,当备选序列数为16时,CSLM算法所对应的RCM0为7.30 dB,WSLM算法对应的RCM0为7.50 dB,BSLM算法和MBSLM算法对应的RCM0均为7.90 dB。因此,MBSLM算法的RCM抑制性能与BSLM算法相同,仅比CSLM、WSLM算法分别差0.60 dB和0.40 dB。当备选序列数增加到81时,MBSLM算法与CSLM、WSLM算法的RCM性能差距进一步缩小,仅比CSLM算法和WSLM算法分别差0.40 dB和0.35 dB。因此,MBSLM算法明显降低了发送端的计算复杂度,同时获得了良好的RCM抑制性能。

图6　各种算法的RCM性能曲线

在产生相同备选序列数的情况下,以K=81为例,CSLM算法所需的相位因子序列数为81,WSLM算法所需的相位因子序列数为9,而BSLM算法和MBSLM算法所需要的相位因子序列数为3。一方面,根据算法原理,MBSLM算法与BSLM算法产生时域备选序列一致,因此二者的PAPR和RCM性能相当,但MBSLM算法的复杂度明显低于BSLM算法;另一方面,MBSLM算法是通过较少的相位因子序列数和较少的IFFT运算获得多个时域备选序列,备选序列之间的独立性略差,因此在PAPR和RCM性能上会稍差于CSLM和WSLM算法,但该算法的优点是显著降低了发送端的计算复杂度,且获得了良好的PAPR和RCM抑制性能。

4.2BER性能分析

本文仿真分析了两种信道模型下CSLM算法(边带信息已知)、WSLM(边带信息已知)、MBSLM算法(边带信息已知)和MBSLM算法(盲检测方式)的BER性能。

如图7所示,在AWGN信道模型中,本文提出的盲检测算法的BER性能曲线与已知边带信息的情况基本一致。当Eb/N0小于10 dB时,盲检测方式下算法的BER性能比已知边带信息的情况要差一些,这是因为信噪比较低时,接收端检测相位因子会受到噪声的影响,相位因子恢复误差会导致系统的BER性能恶化,所以在低信噪比条件下采用盲检测方式比已知边带信息方式的BER性能稍差。当Eb/N0大于10 dB时,接收端的相位因子恢复误差较小,盲检测方式能够较准确地估计出原始相位因子序列,能够获得与已知边带信息的情况下相同的BER性能。因此,在高斯信道中当信噪比Eb/N0大于10 dB时,本文提出的盲检测方式能够有效地恢复原始信号。

图7　AWGN信道中各算法的BER曲线

当备选序列数为16时,在Eb/N0为30 dB处,CSLM算法对应的BER=3.67×10-4,WSLM算法对应的BER为3.98×10-4、MBSLM算法对应的BER为4.87×10-4;当备选序列数为81时,在Eb/N0为30 dB处,CSLM算法对应的BER为1.56×10-4,WSLM算法对应的BER为1.62×10-4,MBSLM算法对应的BER为2.13×10-4,因此可以看出,在相同备选序列数下,MBSLM算法的BER性能略差于CSLM算法和WSLM算法,随着备选序列数的增加,二者的BER性能差距减小。但由表1和表2可知,MBSLM算法发送端的计算复杂度明显低于CSLM算法和WSLM算法,且不需要传送边带信息,能够提高频谱利用效率。

如图8所示,在EVA70信道模型中,在满足一定信噪比条件下,本文提出的盲检测算法能够获得与已知边带信息情况下相同的BER性能。当Eb/N0小于15 dB时,由于在低信噪比下,接收端检测相位因子会受到噪声的影响,相位因子恢复误差会导致系统的BER性能恶化,所以盲检测方式下算法的BER性能比已知边带信息的情况下要差一些;随着Eb/N0增加到15 dB后,接收端的相位因子恢复误差较小,盲检测方式能够较准确地估计出原始相位因子序列,能够获得与已知边带信息的情况下相同的BER性能,因此,在EVA70信道中,当信噪比Eb/N0大于15 dB时,本文提出的盲检测方式能够有效地恢复原始信号。

图8　EVA70信道中各种算法的BER曲线

在Eb/N0为35 dB处,当备选序列为16时,CSLM、WSLM、MBSLM算法对应的BER分别为6.16×10-4、6.53×10-4、7.67×10-4;当备选序列数K=81时,CSLM、WSLM、MBSLM算法对应的BER分别为3.89×10-4、4.12×10-4、4.38×10-4。因此,可以看出,在相同备选序列数下,MBSLM算法的BER性能稍差于CSLM算法和WSLM算法,当备选序列数增加到81时,性能差距逐渐减小。同时,由表1和表2可知,MBSLM算法发送端的计算复杂度远低于CSLM算法和WSLM算法,且不需要传送边带信息,能够提高频谱利用效率。

5结论

本文针对传统SLM算法的高计算复杂度和边带信息等问题,提出了一种基于盲检测的低复杂度分块SLM算法。该算法的发送端利用IFFT性质,通过少量低维IFFT运算获得多个时域备选序列,算法的接收端采用低复杂度的盲检测方式,不需要额外的边带信息。通过对算法仿真得到,当备选序列个数相同时,所提算法的计算复杂度明显低于传统SLM算法,且有效抑制了OFDM信号的PAPR和CM,在盲检测方式下获得了良好的BER性能,提高了频谱利用效率。

参考文献：

[1] Kitaek B, Powers E J. Performance analysis of OFDM systems with selected mapping in the presence of nonlinearity[J].IEEETrans.onWirelessCommunications, 2013, 12(5): 2314-2322.

[2] Zhu X D, Pan W S, Li H. Simplified approach to optimized iterative clipping and filtering for PAPR reduction of OFDM signals[J].IEEETrans.onCommunications, 2013, 61(5): 1891-1901.

[3] Wang Y, Wang L H, Ge J H. Nonlinear companding transform technology for reducing PAPR of OFDM signal[J].IEEETrans.onConsumerElectronics, 2012, 58(3): 752-757.

[4] Singh E, Arif M, Shrivastava V. Nonliear companding technique for PAPR reduction in OFDM[C]∥Proc.oftheIEEEInternationalConferenceonSignalPropagationandComputerTechnology,2014: 801-805.

[5] Zhang S, Yang L,Li S Q. A algorithm combined PSO and factor optimal pair for PAPR reduction in OFDM system[J].SystemEngineeringandElectronics,2012,34(7):1479-1483.(张帅,杨霖,李少谦.POS与相位因子优选对结合降低OFDM峰均比的算法[J].系统工程与电子技术,2012,34(7):1479-1483.)

[6] Zhang S, Ge J H, Gong F K. Partial transmit sequence using EVM optimization metric for BER reduction in OFDM systems[C]∥Proc.ofthe8thInternationalConferenceonCommunicationsandNetworking,2013:113-117.

[7] Rahmatallah Y, Mohan S. Peak-to-average power ratio reduction in OFDM systems: survey and taxonomy[J].IEEECommunicationsSurveyandTutorials, 2013, 15(4): 1567-1592.

[8] Tsai Y R, Lin C H, Chen Y C. A low-complexity SLM approach based on time-domain sub-block conversion matrices for OFDM PAPR reduction[C]∥Proc.oftheIEEESymposiumonComputersandCommunications, 2011: 579-584.

[9] Yoo H, Guiloud F, Pyndiah R. Low complexity SLM technique with an inter-leaver butterfly ensemble for PAPR reduction of power limit OFDM system[C]∥Proc.ofthe73rdVehicularTechnologyConference,2011: 1-5.

[10] Yang L, Soo K K, Siu Y M, et al. A low-complexity selected mapping scheme by using time domain sequence superposition technique for PAPR reduction in OFDM system[J].IEEETrans.onBroadcasting, 2008, 54(4): 821-824.

[11] Jin S W, Ji H L, Jae C P, et al. Combining of cyclically delayed signals: a low-complexity scheme for PAPR reduction in OFDM systems[J].IEEETrans.onBroadcasting,2010,56(3):577-583.

[12] Fischer R F H. Widly-linear selected mapping for peak-to-average power ratio reduction in OFDM[J].ElectronicsLetters, 2007, 43(14):766-767.

[13] Lin P Y, Lin J S. A novel block SLM scheme for PAPR reduction of OFDM systems[C]∥Proc.oftheIEEEInternationalConferenceonSignalProcessing,CommunicationandComputing, 2012: 578-582.

[14] Lu G, Wu P, Aronsson D. Peak-to-average power ratio reduction in OFDM using cyclically shifted phase sequences[J].IETCommunications, 2007, 1(6): 1146-1151.

[15] Deumal M, Behravan A, Pijoan J L. On cubic metric reduction in OFDM systems by tone reservation[J].IEEETrans.onCommunications, 2011, 59(6): 1612-1620.

[16] Bohara V, Ting S. Theoretical analysis of OFDM signals in nonlinear polynomial models[C]∥Proc.ofthe6thInternationalConferenceonCommunications, 2007: 1-5.

[17] Mitra S K.Digitalsignalprocessing,acomputerbasedapproach[M]. Benjing: Publishing House of Electronics Industry, 2005: 110-120.

[18] Jayalath A D S, Tellambura C. SLM and PTS peak-power reduction of OFDM signals without side information[J].IEEETrans.onWirelessCommunications, 2005, 4(5): 2003-2013.

[19] Stefania S,Lssam T.TheUMTSlongtermevolutionfromthorytopractice[M]. Beijing: Posts & Telecom Press, 2009.

杨霖(1977-),男,副教授,博士,主要研究方向为无线与移动通信、现代通信中的信号处理。

E-mail:eelyang@uestc.edu.cn

何向东(1991-),男,硕士研究生，主要研究方向为现代通信中的信号处理。

E-mail:984078297@qq.com

刘雲雲(1991-),女,硕士研究生,主要研究方向为无线与移动通信中SCMA系统的码本分配和MPA译码算法。

E-mail:1576406014@qq.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150916.1551.008.html

Low complexity block SLM based on blind detection in OFDM systems

YANG Lin, HE Xiang-dong, LIU Yun-yun

(NationalKeyofLaboratoryofScienceandTechnologyonCommunications,Universityof

ElectronicScienceandTechnology,Chengdu611731,China)

Abstract:In order to reduce the computational complexity and improve the spectrum efficiency of the conventional selected mapping (CSLM) algorithm in orthogonal frequency division multiplexing (OFDM) systems, a low complexity block selected mapping (BSLM) algorithm based on blind detection is proposed. In the method, the transmitting part only needs a few low-dimensional inverse fast fourier transform (IFFT) operations to obtain a lot of alternative sequences, at the same time, the receiving part uses a modified blind detection to reduce the complexity. The performance of the peak to average power rate (PAPR), cubic metric (CM) and bite error rate (BER) is analyzed. Simulations show that the proposed method can not only reduce the computational complexity significantly, but also control PAPR and CM of the OFDM signal effectively, as well as it can obtain similar BER performance to that of the conventional SLM with perfect side information.

Keywords:orthogonal frequency division multiplexing (OFDM); peak to average power ratio (PAPR); cubic metric (CM); selected mapping (SLM); blind detection

作者简介：

中图分类号：TN 919.3

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.01.26

基金项目：国家自然科学基金(61370012)；国家重点基础研究发展计划(973计划)(2013CB316003)资助课题

收稿日期：2015-04-30；修回日期：2015-07-14；网络优先出版日期：2015-09-16。