绩效导向下的武器装备采购系统再投入比例控制

尹铁红, 谢文秀, 李忠光

(1. 装备学院装备采办系, 北京 101416; 2. 中国人民解放军96251部队,

河南 洛阳 471000; 3. 军事交通学院装备管理系, 天津 300000)



绩效导向下的武器装备采购系统再投入比例控制

尹铁红1,2, 谢文秀1, 李忠光3

(1. 装备学院装备采办系, 北京 101416; 2. 中国人民解放军96251部队,

河南 洛阳 471000; 3. 军事交通学院装备管理系, 天津 300000)

摘要：以武器装备采购系统技术创新再投入比例控制为研究对象,综合运用经济学、控制论等相关理论,采用模型推演、数据演算、仿真验证等方法,对技术创新再投入与系统发展绩效的关系进行了理论分析和实证检验。区分单系统和全系统,就技术创新再投入比例的优化及实现路径进行了探讨,为我军武器装备采购宏观调控政策的制定完善提供依据和参考。

关键词：武器装备采购; 发展绩效; 技术创新投入; 比例控制

0引言

运用全寿命周期理论分析,武器装备采购系统包括科研、生产、购置、用户和服务5个子系统。其中,科研、生产和服务3大供给系统的可持续发展特性直接影响武器装备采购系统的整体绩效。在这3大系统中,技术创新能力是实现系统可持续发展,提高武器装备采购系统整体绩效的重要影响因素,加大技术创新投入力度是提高系统持续发展进步的有效手段。适应当前国家经济发展模式从数量规模型向质量效益型转变的趋势要求,武器装备采购系统的技术创新再投入规模的大小及其合理性问题,成为武器装备采购实践中的一大难题,更是我军采购领域需要探讨和迫切需要解决的问题。因此,从经济理论、控制理论及技术方法等方面研究武器装备采购系统技术创新再投入比例的优化问题具有重要的理论和现实意义[1-4]。

1技术创新投入与采购系统发展作用机理分析

20世纪,康德拉季耶夫、熊彼特、库兹涅茨、门斯、弗里曼等多位经济学家系统研究了技术创新与宏观经济增长之间的对应关系,研究发现,经济繁荣的长波周期背后必然蕴藏着新技术创新群的突发和转移,技术创新与经济发展之间存在着因果关系,技术创新的高峰带来经济发展的繁荣,技术创新的低谷引起经济的萧条。历史和实践的经验证实,技术创新不仅影响着经济的发展,而且决定着企业的兴衰和产业的演变,国际、国家、区域以及产业、企业创新体系的构筑越来越受到专家学者的关注。在当今知识信息高度融合发展的时代,技术创新成为产业系统持续发展的内在动力和源泉。武器装备采购系统运行机制是指军工科研、生产、服务等供应系统与军队购置、用户等需求系统相互作用形成的稳定模式。它的主要功能是使供应系统作为自组织系统,与军队需求系统形成良性互动。技术创新型的武器装备采购系统具有正反馈性,在这种模式下,供应系统不断通过技术创新向需求系统提供优质武器装备和服务,从而获得军方提供的信息、资金等创新资源,这种正反馈运行机制是供应系统不断发展的基础,一方面,军方要通过采购体系建设,为形成这种机制提供可能,另一方面,供应系统要通过技术创新再投入建立自己的“可持续发展动态生态系统”。技术创新型供应系统可持续发展机制具有2个基本特点:一是技术创新是武器装备供应系统取得利润的源泉;二是技术创新再投入是持续获利的基础。有学者指出,成功企业的研发再投入比例占到总产值(销售额)的10%~20%,高技术产业已占到30%以上[5-9]。

2单系统再投入比例控制

2.1最佳再投入比例控制的基本思想

武器装备供应系统运行的目的是为军方需求系统提供符合性能指标要求的武器装备,同时也为供应系统发展赢得利润收入,收入的一部分用于积累,满足供应系统资金运转和设备折旧,另一部分则用于技术创新投资,从而保证系统再发展、再生产的顺利进行。如果积累偏低,就会影响到供应系统的正常运转;相反,如果积累偏高,技术创新投入偏低,就会影响供应系统的持续发展能力,从而导致武器装备技术性能和生产效率降低。因此,技术创新再投入和资金积累之间应当建立一个合适的比例,也就是解决供应系统收入合理分配问题。柯布·道格拉斯生产函数可以设定技术水平一定的条件下,使积累率达到最大,但不能满足在收入一定的条件下使技术创新投入达到最大。为解决上述问题,本文以劳动力数量一定条件下的道格拉斯生产函数和技术力增长函数为基础构建状态方程,建立单位技术创新力再投入累积量最大的目标函数,并应用庞特立亚金极大值理论,对技术创新再投入比例进行最优化求解[10-13]。

2.2状态方程和目标函数构建

设t时刻某一供应系统的利润收入为Z(t),用于积累的资金为J(t),技术创新再投入为T(t),则3变量的经济关系式为

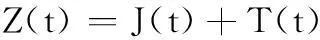
(1)

设定s为积累率,(1-s)为技术创新再投入率,且0≤s≤1,则

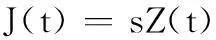
(2)

(3)

设Q(t)为系统用于运作和设备更新的资金量,则积累量可表示为

(4)

式中,γ表示折旧率。

设G(t)为t时刻系统的技术力,并且系统的劳动力保持不变,A为固定比例系数,则道格拉斯生产函数可表示为

(5)

将式(5)两边同时除以G(t)得

(6)

(7)

将式(4)两边同时除以G(t)得

(8)

由式(2)、式(7)可得

(9)

由式(9)可得

(10)

设系统技术力增长函数为

(11)

该函数是表征所研究系统技术力变化规律的函数,G0表示技术力初始值,G表示该系统经过t时间后的技术力值,其值大小直接影响系统的利润值。ω为技术力增长指数,其值大小与系统技术力增长速度密切相关,系统技术创新发展越快,ω越大;反之越小。

由式(11)得

(12)

将式(12)带入式(10)得

(13)

式(13)即为系统的状态方程。

技术创新再投入比例(1-s)最优控制问题可归结为:确定控制变量s,使0到t时间段的系统平均技术创新资金投入的累积量达到最大,即

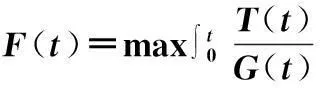
(14)

式中,δ代表平均利率。

由于

(15)

将式(15)带入式(14),目标函数化为

(16)

状态方程为

(17)

边界条件为

2.3最优控制比例求解

运用庞特里亚金极大值理论求解上述问题,构造哈密尔顿函数:

(18)

将式(18)化解为

(19)

由式(19)可知,求解H函数最大值,等价于求解下式极大值,即

(20)

令φ=me-δ t,则

(21)

由式(21)可知,求L最大值可转化为求[1+(m-1)]最大值。因此,m与s有如下对应关系：

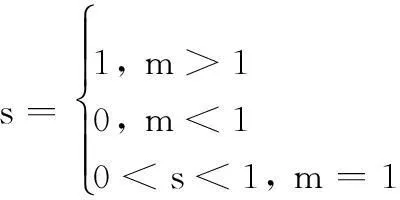
(22)

又

(23)

(24)

由式(23)、式(24)得

(25)

由于s取值为0、1的两种情况与实际不符,s取值只能在0、1之间,由式(22)可知,m=1,将m=1带入式(25),则有

(26)

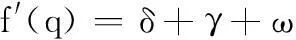
(27)

又

(28)

由式(27)、式(28)得

(29)

所以

(30)

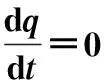
由式(17)可知

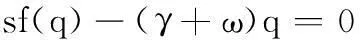
(31)

由式(7)、式(31)得

(32)

将式(30)带入式(32)可得

(33)

由式(33)可得技术创新再投入比例为(1-s),即

(34)

2.4应用示例

以某科研系统为例,依据其2007~2013年间的相关统计数据,确定该系统2014年的技术创新再投入最优控制比例。

(1) 根据其2007~2013年的技术创新力统计数据建立GM(1,1)模型,代入技术力增长函数,可求得技术创新力增长指数为:ω=0.0618。

(2) 依据银行7年的平均利率计算,可得平均利息率为:δ=0.03。

(3) 依据式(2)~式(5)道格拉斯生产函数进行数值模拟,可求得弹性系数的取值范围为:α=0.66-0.78。

(4) 根据式(2)~式(4),经过模拟计算可得折旧率为:γ=0.017 8。

(5) 将各参数代入式(34),可得该系统术创新再投入最优控制比例为:τ=0.43-0.52。

此最优化比例取值是指技术创新投入占系统利润收入的比值,若换算为系统总产出的比值,其取值相应会变小。由于最优再投入比例是通过理论推导求出的,在实际情况下,随着系统内各种费用消耗的增加,实际投入可能低于这个值。另外,科研系统与其他系统相比,其技术创新投入对系统利润的影响更加明显,对应求得的再投入比例值相对较高。

3全系统再投入比例控制

3.1系统模型建立

武器装备采购供应系统主要由科研、生产、服务等3个子系统构成,各系统2007~2013年的投入、产出值如表1所示,依据系统控制相关理论,武器装备采购供应系统若要保持持续的发展态势,必然要求其产出值按照一定的比例正反馈至系统的投入,用于技术创新投资。确定全系统技术创新再投入比例是本模型构建的目标,遵循的原理是通过构建系统正反馈模型(见图1),求解使系统具有发散特性的再投入比例的临界值(比例值太大,造成过度投入,浪费资源;比例值太小,系统不能保持发散特性,影响持续发展),即为全系统的技术创新再投入的最优控制比例[14-17]。

表1　武器装备采购供应系统投入、产出值

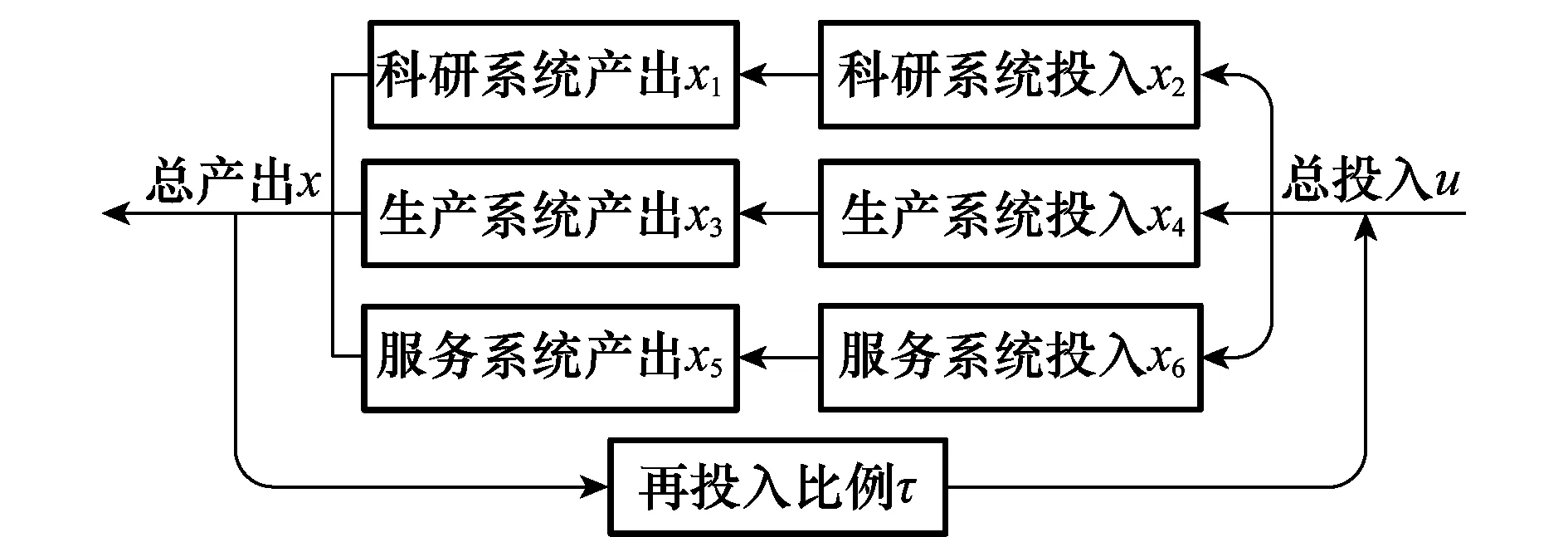
图1　供应系统再投入比例控制模型

3.2系统动态特性分析

依据表1武器装备采购供应系统各子系统的投入、产出数据,运用灰色建模软件,分别建立科研、生产、服务系统的投入、产出GM(1,2)模型为

(35)

(36)

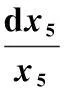
(37)

由式(35)~式(37)建立该控制系统的状态方程为

由此可得,该系统的系数矩阵为

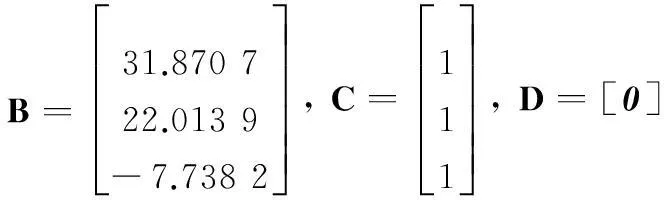
根据系统的系数矩阵,对系统可控性和可观性进行判断如下:

由于系统的可控性、可观性判断矩阵均满秩,可得出结论,该系统可控并且可观。

由科研、生产、服务系统的GM(1,2)模型推导出3个系统的传递函数为

(38)

(39)

(40)

设定武器装备采购供应系统总投入按照0.2、0.4、0.4的比例在科研、生产、服务系统之间进行分配,则系统的总传递函数为

(41)

由式(41)可知,系统的特征方程为

F(s)=1.235 s3+(5.796-20.41τ)s2+

(7.126-53.93τ)s+(1-15.32τ)

(42)

根据系统特征方程,运用劳斯判据或赫尔维茨判据可以对系统的稳定性进行判定。同样,根据上述2个判据也可对系统进行发散判定,在进行系统发散判定时,无须构造劳斯判断矩阵或赫尔维茨判断矩阵,根据特征方程系数的正负取向直接可以对系统进行发散判定。若系统发散,特征方程系数符号相反,并交替出现。因此,系统发散的条件由下述方程组确定:

(43)

解方程组,求得系统发散的条件为

τ>0.28或τ<0.132 1或τ>0.065

3.3系统仿真验证

运用Simulink仿真工具对上述系统模型进行仿真,验证其计算结果是否能够使系统保持持续发展的特性。

根据武器装备采购供应系统的比例控制模型和科研、生产、服务3个子系统的传递函数,设计系统的仿真模型如图2所示。

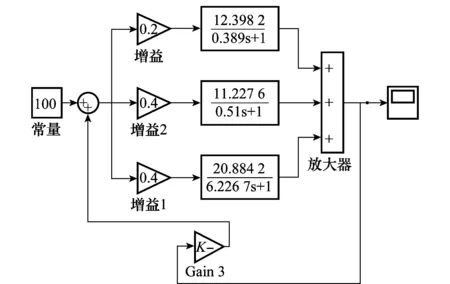
图2　系统再投入比例控制仿真模型

运用上述模型,通过调整反馈比例参数τ的数值,观察系统的输出变化,最终确定τ的最合理取值。

当τ=0.65时,系统输出如图3所示。

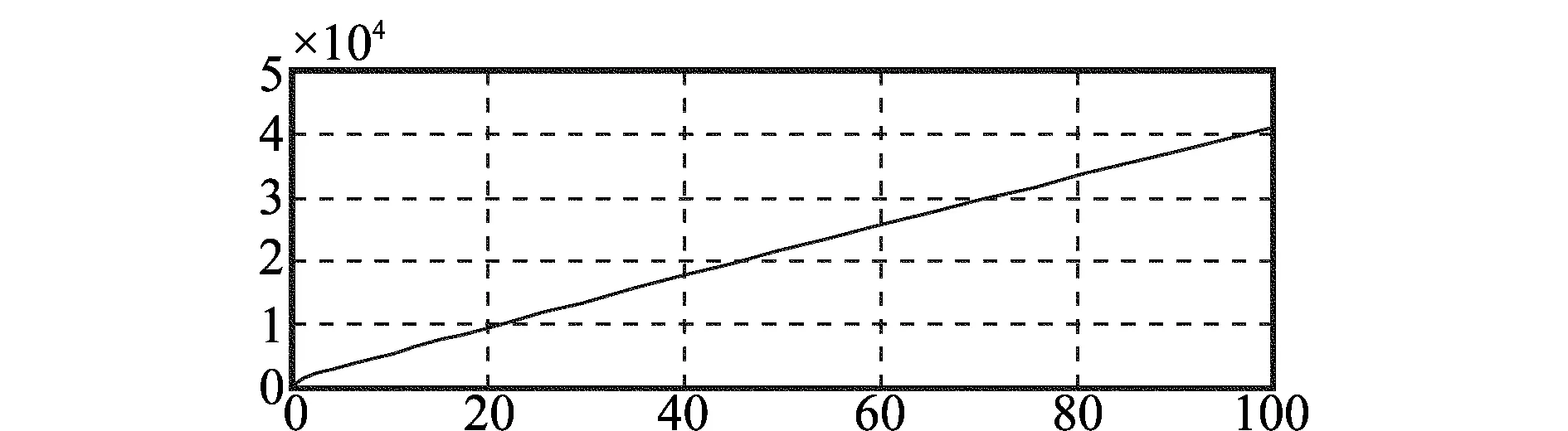
图3　τ=0.65时系统输出曲线

当τ=0.07时,系统输出如图4所示。

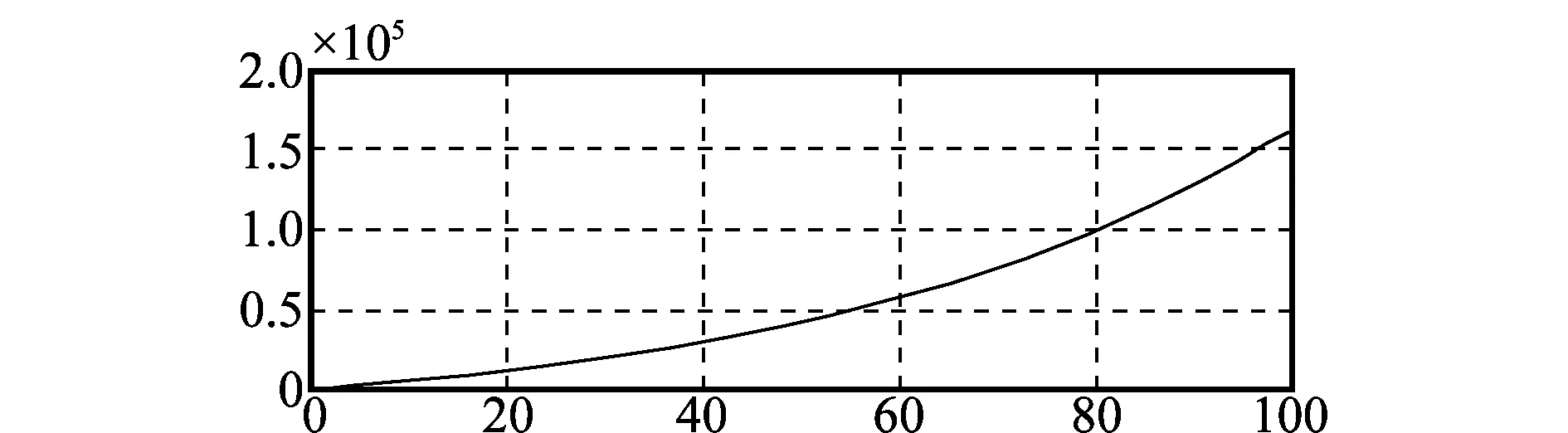
图4　τ=0.07时系统输出曲线

当τ=0.06时,系统输出如图5所示。

图5　τ=0.06时系统输出曲线

当τ=0.15时,系统输出如图6所示。

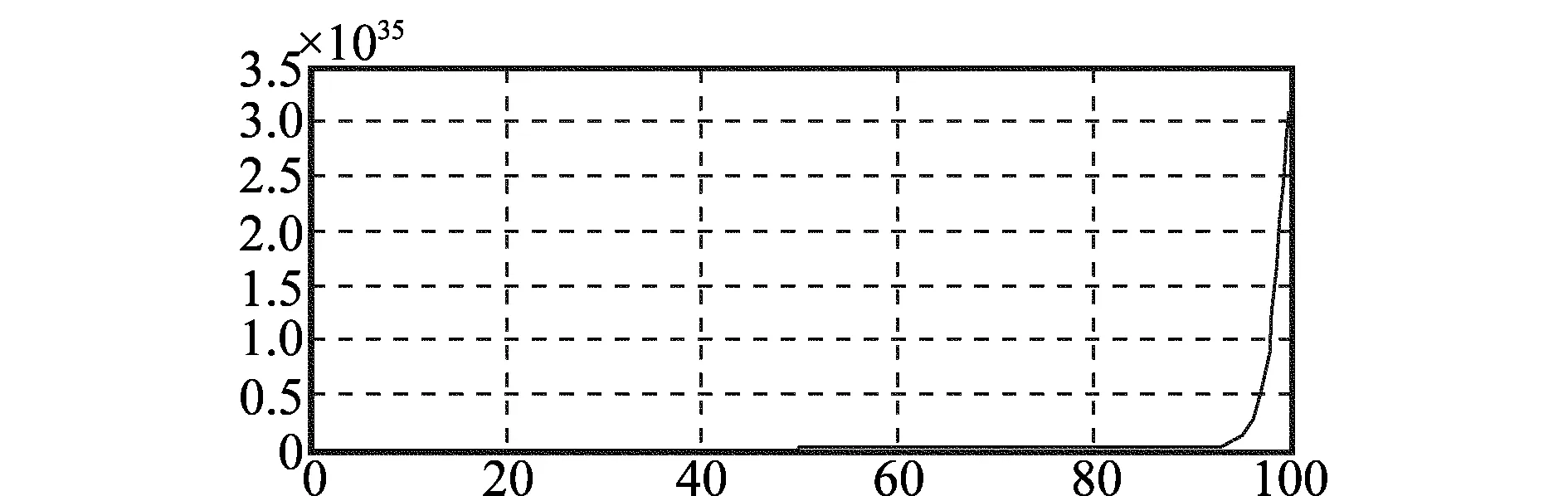
图6　τ=0.15时系统输出曲线

当τ=0.2时,系统输出如图7所示。

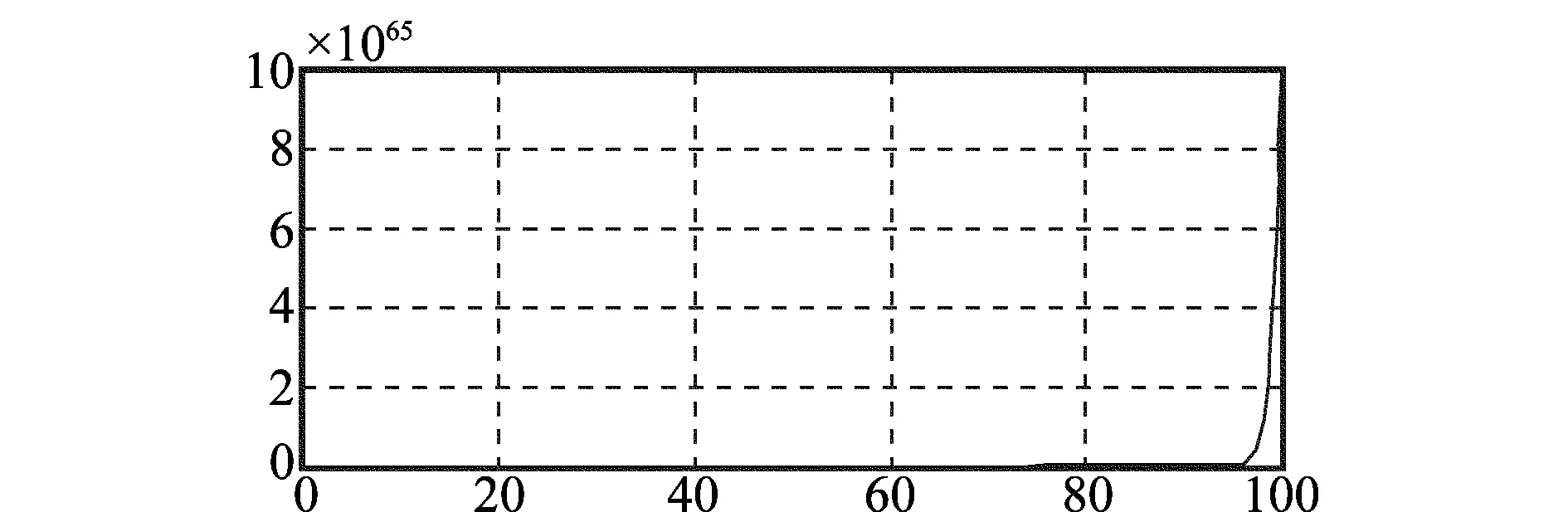
图7　τ=0.2时系统输出曲线

分析上述实验结果,当τ=0.15>0.132 1时,系统仍然呈发散态势,τ<0.132 1的取值结果不可取。同理,当τ=0.2>0.28时,系统也呈现出发散态势,τ>0.28的取值结果也不可取。

当τ=0.065时,系统输出呈现出趋近于直线的增长方式;当τ=0.07时,系统输出呈现出较缓的发散趋势;当τ=0.06时,系统输出呈现出较缓的趋近稳定的趋势。因此,可以判断τ=0.065是系统输出由稳定变为发散的临界值,此值即为武器装备采购供应系统再投入最优控制比例。

综合上述分析可见,系统特性不仅与特征方程系数的符号有关,而且阶数越低的系数对系统特性的影响越大。所以,此系统的发散特性最终由特征方程的0阶常数项决定,即τ>0.065。

4结论

本文以技术力增长函数、道格拉斯生产函数为基础,以单位技术力累积投入量最大化为目标,运用庞特里亚金极大值理论构建哈密尔顿函数,推导出武器装备采购供应单系统技术创新再投入最优控制比例。运用控制理论对武器装备采购供应系统进行投入、产出特性分析,以系统可持续发展为目标,求解全系统技术创新再投入比例,通过构建系统仿真模型对计算结果进行仿真验证,确定最终合理控制比例。运用本文研究结果,可以从宏观上对武器装备采购系统可持续发展绩效进行调控,使武器装备采购绩效管控从项目控制拓展至系统控制,在理论上可促进武器装备采购绩效理论的丰富完善,在实践中可为武器装备采购系统宏观决策提供借鉴和参考。

参考文献：

[1] Xiong B. Research on foreign military procurement performance audit[J].TheAuditofEconomicPerformance, 2009, 38(3): 37-39.(熊斌.外军装备采购绩效审计研究[J]. 经济效益审计,2009, 38(3): 37-39.)

[2] Wang J G.Basictheoryresearchonequipmentprocurement[M]. Beijing: Defense Industry Press,2009:398-413.(王建国.装备采购基础理论研究[M]. 北京:国防工业出版社,2009:398-413.)

[3] Li M.Analysisofequipmentprocurementeconomicproblem[M]. Beijing: Defense Industry Press,2007:96-133.(李鸣. 装备采购经济问题分析[M].北京:国防工业出版社,2007:96-133.)

[4] Yu G D.Thescienceofmilitaryequipment[M]. Beijing: Defense Industry Press, 2009: 258-274.(余高达. 军事装备学[M]. 北京:国防大学出版社,2009:258-274.)

[5] Andreas P. The role of sequential innovation and R & D workers in limiting scale effects[J].TheJournalofInterdisciplinaryEconomics, 2009,16(2): 207-216.

[6] Denicolo V. The secrets and the first inventor defense[J].JournalofEconomicsandManagementStrategy, 2012, 13(3): 517-538.

[7] Eugenio J. Innovation complementary and scale of production[J].TheJournalofIndustrialEconomicsMarch, 2010, 66(1): 1-30.

[8] Hans L. R&D networks and product innovation patterns-academic and non-academic new technology-based firms on science parks[J].Technovation, 2011, 25(3): 1025-1037.

[9] Larry H. Connect & develop: inside proctor & gamble’s new model for innovation[J].HarvardBusinessReview, 2010, 68(3): 58-66.

[10] Wang Y C. Several methods of optimal control[J].JournalofHuaqiaoUniversity, 2006, 27(1): 68-70.

[11] Frank L.Optimalcontrol[M]. New York:Wiley, 2006: 15-27.

[12] Franklim G F.Digitalcontrolofdynamicsystems[M]. New York: Addison-Wesley, 2006: 422-450.

[13] William L B.Moderncontroltheory[M]. London: Prentiee-Hall, 2009: 443-460.

[14] Wang H L. Qualitative modeling and simulation of complex system based on the combination of GM(1,N) and QSIM[J].CAAITrans.onIntelligentSystem, 2013, 8(4): 367-371.

[15] Hu B. Qualitative simulation of complex system[J].TechnologyofSystemSimulation, 2006, 2(1): 1-11.

[16] Hu B. Qualitative simulation of group behavior in information integrating CA and QSIM[J].ChineseManagementScience, 2005, 13(5): 130-136.

[17] Chen Z H. Development of qualitative and quantitative intelligent simulation[J].AutomationReviews, 2005, 1(3): 4-8.

尹铁红(1977-),男,博士研究生,主要研究方向为装备采办。

E-mail:YTH13264073731@163.com

谢文秀(1963-),女,博士,主要研究方向为装备采办。

E-mail:13611099291@139.com

李忠光(1974-),男,博士研究生,主要研究方向为装备保障。

E-mail:18622135927@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150817.1821.016.html

Feedback proportional control under the guide of performance in

the system of weapons and equipment acquisition

YIN Tie-hong1,2, XIE Wen-xiu1, LI Zhong-guang3

(1.DepartmentofEquipmentAcquisition,EquipmentAcademy,Beijing101416,China; 2.Unit96251ofthePLA,

Luoyang471000,China; 3.DepartmentofEquipmentManagement,MilitaryTransportationAcademy,Tianjin300000,China)

Abstract:How to control the proportion of technological innovation investment in the system of weapons and equipment acquisition is researched. The relationship between technology investment and system development performance has carried on the theoretical analysis and empirical test using the methods of model deduction, data calculation and simulation experiment based on the theories of economics and cybernetics. The single system and the whole system are distinguished, and the optimization and realization of the feedback proportion of technological innovation investment are discussed. Research results provide reference for the establishment and development of weapons and equipment procurement macro-control policies.

Keywords:weapons and equipment acquisition; development performance; technological innovation investment; proportional control

作者简介：

中图分类号：E 917

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.01.16

基金项目：军队研究生资助课题

收稿日期：2014-12-26；修回日期：2015-03-13；网络优先出版日期：2015-08-17。