Q460D高强钢断裂性能试验研究及断裂准则的校准

廖芳芳，李文超，周天华

(长安大学建筑工程学院，陕西 西安 710061 )

断裂作为结构钢材的一种重要失效模式一直以来是业内研究的热点.目前，对于结构钢材断裂性能的研究多集中于常用的Q235钢和Q345钢[1]，而对近年来应用于结构工程领域当中的高强度钢材的断裂性能研究却较为少见.与常用的Q235钢和Q345钢相比，高强度钢材具有高强、轻质、经济等优点，但是随着钢材屈强比的增加，材料延性变差，断裂成为高强度钢材突出的问题[2].加之高强度钢材多应用于大型、超高层及关乎民生的重要性建筑中，研究高强度钢材的断裂性能对预测结构失效问题及防灾减灾具有重要的意义.

结构钢材作为多晶体金属材料，其断裂性能取决于材料的微观结构及所处应力状态.在不同应力状态下（如拉伸、剪切、压缩、复合应力状态），结构钢材表现出明显不同的断裂性能.标准的单轴拉压材性试验只能用于获取钢材在单轴应力状态下的断裂性能.而在实际工程当中，钢材的断裂通常始于结构中几何形状复杂的“切口”部位.一方面，加工引起的微观缺陷多集中于这些部位；另一方面，因“切口”几何不连续性所引起的应力集中及多轴应力状态均汇集于此.因此需要充分考察结构钢材在多轴应力状态下的断裂性能.

本文对我国具有广泛应用前景的Q460D高强度结构钢材静力状态下的延性断裂性能进行了试验研究.分别对切口圆棒试件、剪切型及拉剪型平板切口试件、平板槽口试件进行了断裂试验，并利用扫描式电子显微镜对各切口试件的断口表面进行了观察分析，考察了应力状态对Q460D钢延性及微观断裂机制的影响，从而为提出合理的微观断裂准则提供依据.

1 结构钢材的断裂应变及应力状态

在多轴应力状态下，结构钢材的延性可由材料断裂前所承受的等效塑性应变（后文称为断裂应变）来衡量.在单调加载情况下，钢材的断裂应变可表示为如下形式：

早期的研究表明[3-7]，钢材断裂应变的大小取决于材料所承受的应力三轴度，材料的断裂应变随着应力三轴度的升高明显下降.其中材料的应力三轴度η的表达式如下：

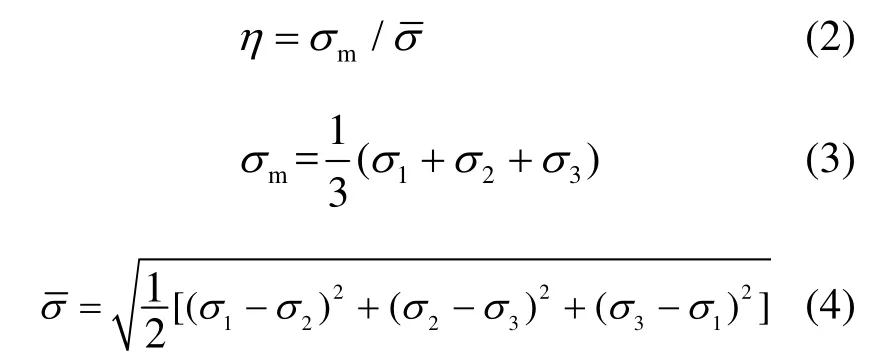
近年研究表明[8-11]，除静水应力外，Lode角参数是影响金属材料塑性流动及断裂性能的另一个重要的应力参数.其中材料的Lode角可以由主应力空间中π平面上与偏应力主轴的夹角进行表示：

式中θ为Lode角(0≤θ≤π/3），ξ为正交标准化的偏应力张量第三不变量（-1≤ξ≤1）.对Lode角θ进行标准正交化，可以得到如下形式[9]：

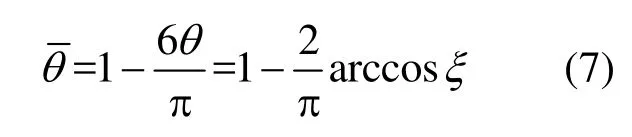
2 Q460D高强度结构钢材切口试件断裂试验

2.1 Q460D结构钢材

试验研究所用的Q460D低合金高强度结构钢由上海宝山钢铁有限公司提供.试验中所有的试件均从厚度为36 mm的Q460D热轧型高强钢板上抽取加工而成.根据出厂报告显示，本批Q460D钢材的名义屈服应力为488 MPa，名义极限应力为618 MPa，钢材伸长率为24%，屈强比为0.79，符合《低合金高强度结构钢》（GB/T1591-2008）[12]中的技术要求.

2.2 试验方案及试件设计

为了考察Q460D钢在不同应力三轴度及Lode角参数状态下的断裂性能，本试验对四种类型切口试件进行了断裂试验，分别包括：平滑/切口圆棒试件拉伸试验、平板切口试件剪切试验、平板切口试件拉剪试验及平板槽口试件拉伸试验.其中，圆棒试件采用数控车床加工而成；平板切口与槽口试件采用低速单向走丝电火花线切割技术加工而成.各试件均从钢板中心部位抽取，试件轴线与钢板轧制方向相同.试验中各试件编号、数量及切口尺寸祥见表1.

2.2.1 平滑圆棒试件

平滑圆棒试件拉伸试验除用于获取结构钢材的本构信息外，还可用于获取钢材应力三轴度为1/3、Lode角参数的断裂应变.平滑圆棒试件的几何尺寸根据美国材料与试验协会ASTM E8/E8M-11[13]中的规定进行设计（见图1(a)及图2(a)），试件标距长度为20 mm，试件总数为3根.圆棒试件加工好后，对试件进行如下编号：BS-1、2、3.各试件标距段中心处所测直径见表1.

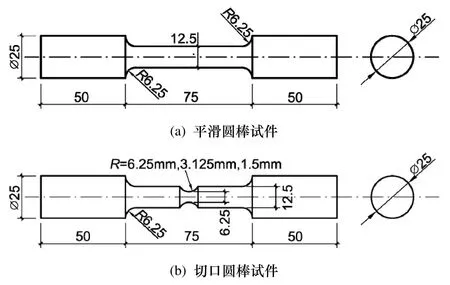
图1 平滑/切口圆棒试件几何尺寸Fig.1 Geometry of the smooth/notched round bar specimens

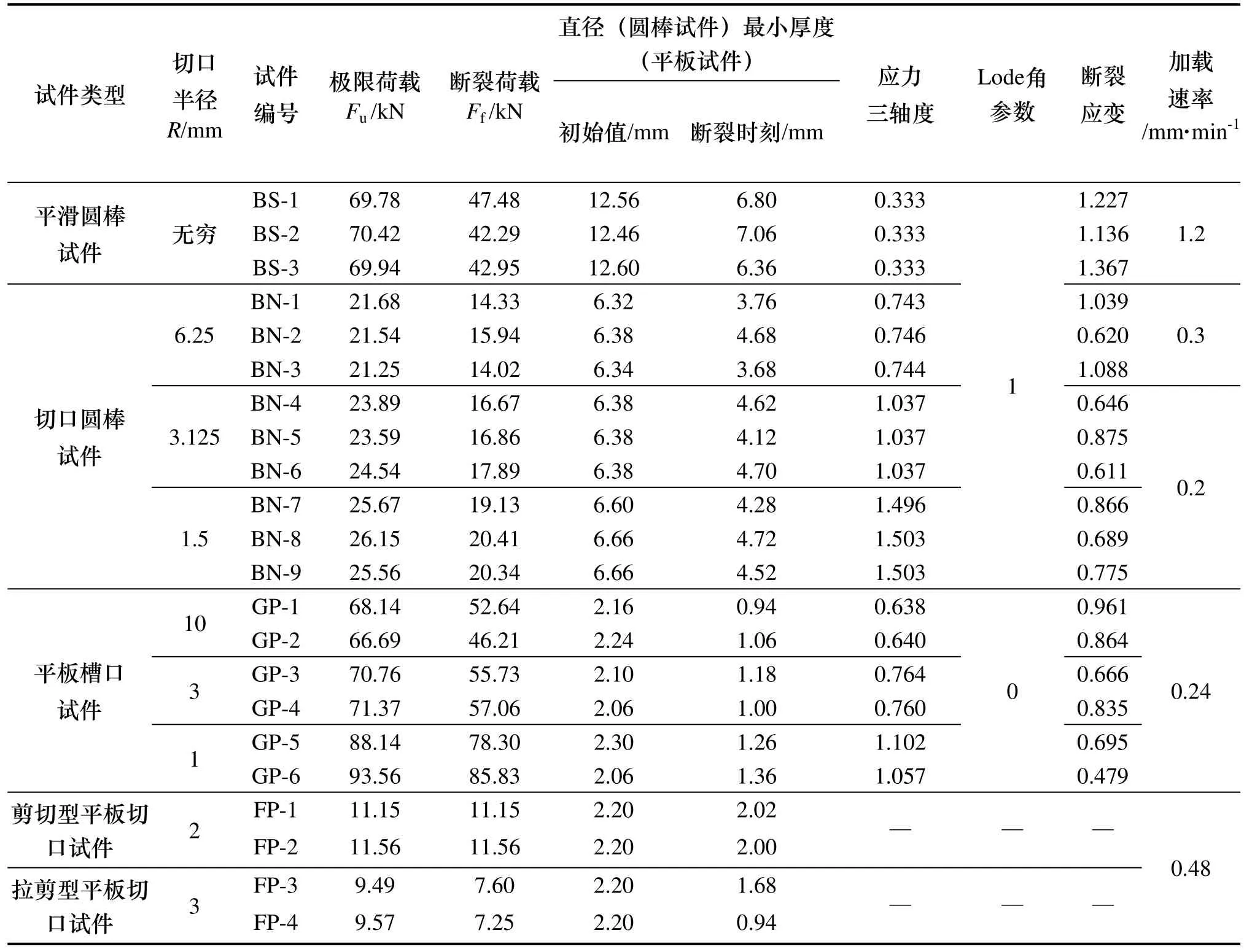
表1 试验中各试件信息汇总Tab.1 Summary of the generated results from tested specimens

2.2.2 切口圆棒试件

对平滑圆棒试件表面引入环向圆弧切口，可在切口根部获得三轴应力状态.本次试验中切口圆棒试件所选用的切口半径分别为6.25 mm、3.125 mm及1.5 mm.各试件切口根部最小截面直径为6.25 mm，其余部位尺寸与平滑圆棒试件相同（见图1(b)及图2(b-d)）.每种类型切口圆棒试件各为3根，试件标距长度均为20 mm.试件加工好后，分别对切口圆棒试件进行如下编号：BN-1-9.经测量，各圆棒试件切口根部最小截面处的初始直径处于6.32～6.66 mm之间（见表1）.

文献[3]给出了切口圆棒试件切口根部最小截面中心部位的初始应力三轴度公式：

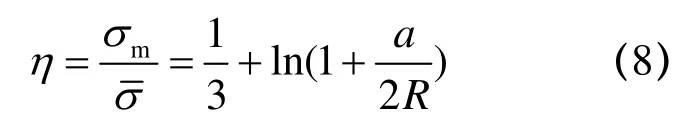
式中R为试件切口圆弧半径，a为切口根部横截面半径.从公式（8）中可以看出，改变切口尺寸可获取不同程度的三轴应力水平.当试件切口半径R趋于无穷时（平滑圆棒试件），试件截面中心处的初始应力三轴度为1/3.各切口圆棒试件的初始应力三轴度及Lode角参数见表1.

图2 平滑/切口圆棒试件实物图Fig.2 Smooth/Notched round bar specimens

2.2.3 剪切型及拉剪型平板切口试件

为了考察Q460D钢在纯剪切应力状态及拉剪复合应力状态下的断裂性能，本文设计了如图3～4中所示的剪切型及拉剪型平板切口试件[14].

剪切型平板切口试件全长180 mm，中心有效截面宽度为60 mm.试件整体呈平面反对称图形，中心标距段呈“蝴蝶型”.两边夹持段沿试件中线开有直径为13 mm的圆孔.试验中，通过在圆孔中插入铰接销栓进行加载.为了保证断裂出现在试件中心标距段内，试件标距段外易产生应力集中部位采取过渡圆弧处理.同时，试件标距段与夹持段采用不同的厚度（夹持段与标距段厚度分别为4 mm和2 mm）.在单轴拉伸作用下，剪切型平板切口试件中心“蝴蝶型”标距段处于纯剪切应力状态，因此可以考察材料在纯剪切应力状态下的断裂性能.

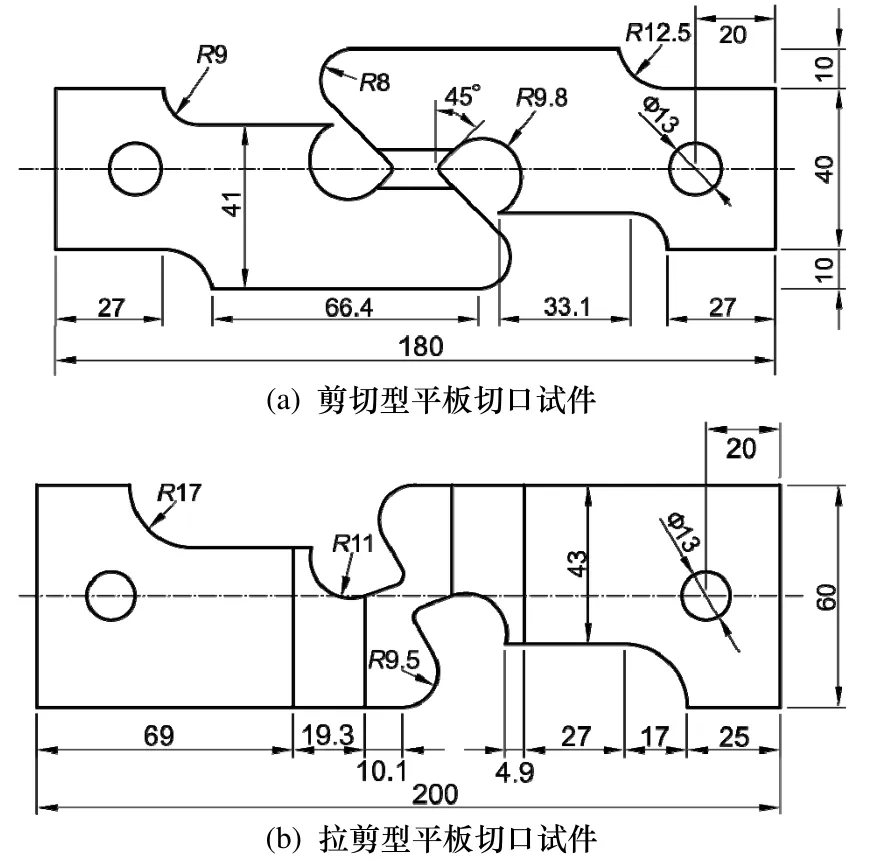
图3 剪切型及拉剪型平板切口试件几何尺寸Fig.3 Geometry of the pure-shear and tensile-shear notched specimens

拉剪型平板切口试件全长200 mm，宽度为60 mm，试件整体呈平面反对称图形.试件中心处设有与轴线呈20°角的斜向标距段，两边夹持段沿试件中线设有直径为13 mm的加载圆孔.试件夹持段与标距段厚度分别为4 mm和2 mm，夹持段与标距段之间采用半径为190 mm圆弧进行过渡，以保证断裂出现在试件标距段内.在单轴拉伸作用下，拉剪型平板切口试件中心斜向标距段处于拉剪复合应力状态，因此可以考察材料在拉剪复合应力状态下的断裂性能.

图4 平板切口及平板槽口试件实物图Fig.4 Notched and grooved plate specimens

试验前，分别对各平板试件进行如下编号：剪切型平板切口试件编为FP-1、2；拉剪型平板切口试件编为FP-3、4，并利用游标卡尺对各试件标距段厚度进行测量.经测量，各试件标距段中心处厚度均为2.20 mm（见表1）.

2.2.4 平板槽口试件

为了考察Q460D钢在平面应变状态下的断裂性能，本文设计了如图5中所示的平板槽口试件（试件实物见图4）.各平板槽口试件分别是在一块长×宽×厚度=150 mm×50 mm×5 mm的矩形薄板基础上加工而成.通过在薄板中部开设对称弧形槽口，从而在槽口根部引入三轴应力状态.本次试验中，平板槽口试件所选用的槽口半径分别为10 mm、3 mm、1 mm，槽口根部最小截面厚度为2 mm.每种半径平板槽口试件数量各为2个，试件标距长度均为20 mm.试件加工好后，分别对各试件进行如下编号：GP-1-6.各试件槽口根部最小截面厚度见表1.

图5 平板槽口试件几何尺寸Fig.5 Geometry of the grooved plate specimens

在单轴拉伸作用下，平板槽口试件槽口中心部位处于平面应变状态.Bridgman给出了平板槽口试件槽口根部最小截面中心处的初始应力三轴度公式[3]：

式中t为试件槽口根部最小截面厚度，R为槽口半径.可以看出，通过改变槽口根部厚度与槽口半径可以获得的应力三轴度.各平板槽口试件的初始应力三轴度见表1.

2.3 试验设备及加载方案

试验加载设备采用MTS-880型电子万能试验机，试验机最大拉力为200 kN.试验中，圆棒及平板槽口试件的轴向应变采用MTS电子应变引伸计测量，引伸计标距长度为20 mm，延伸率为25%，可以获取试件直至断裂时刻的应变数据.试验加载采用位移控制，试验机与引伸计上的数据采集频率为20 Hz.为了准确捕捉各试件标距段内的断裂部位，试验采用较为缓慢的加载速率，并全程布置专人对试件的断裂起始位置进行观测.各试件的加载速率及加载图分别见表1及图6.

图6 试验中各切口试件加载图Fig.6 Loading on the tested specimens

3 试验结果与分析

3.1 平滑圆棒试件试验结果

平滑圆棒试件单轴拉伸试验所获取的工程应力-应变曲线如图7所示.本次试验中，Q460D钢的实测屈服强度约为430 MPa，极限强度约为570 MPa.各圆棒试件获得的钢材材性见表2所示.

图7 Q460D钢的工程应力-应变曲线Fig.7 Engineering stress-strain curves of Q460D structural steel

表2 Q460D钢材材性结果Tab.1 Material properties of Q460D structural steel

3.2 切口圆棒试件试验结果

各切口圆棒试件的荷载-位移曲线如图8所示.从图中可以看出，切口尺寸对试件承载力及延性有明显的影响.切口圆棒试件的屈服及极限荷载随着切口半径的减小而升高（切口半径R=6.25 mm、3.125 mm、1.5 mm试件屈服荷载分别为16.9 kN、18.1 kN、21.1 kN，极限荷载分别为21.7 kN、23.8 kN、26.1 kN），延性则随着切口半径的减小而降低（切口半径R=6.25、3.125、1.5 mm试件断裂时刻的位移分别约为2.4 mm、1.7 mm、1.2 mm）.

图8 切口圆棒试件荷载-位移曲线Fig.8 Load-displacement curves of notched round bars

图9 切口圆棒试件断口形态Fig.9 Fracture topography of notched round bars

此外，图9分别显示了各切口圆棒试件的断口形态.从图中可以看出，各圆棒试件均在切口根部处发生断裂.试件断口表面呈“杯锥形”，断口外围与加载轴线呈45度斜平面.随后，利用游标卡尺对各试件断口处直径进行测量并列于表1当中.依据文献[3]，圆棒试件切口根部最小截面处的平均断裂应变可以表示为如下形式：

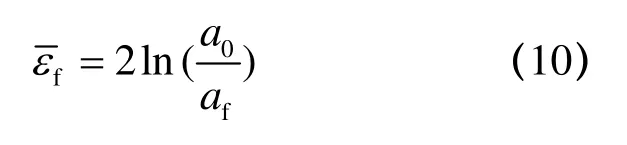
式中：a0为圆棒试件切口根部最小截面的初始半径；af为圆棒试件切口根部最小截面断裂时刻的半径.根据公式(10)所得各圆棒试件的平均断裂应变见表1.

3.3 剪切型/拉剪型平板切口试件试验结果

图10分别显示了剪切型及拉剪型平板切口试件的荷载-位移曲线.如图所示，各平板切口试件屈服台阶较短，硬化阶段较长.由于硬化率衰减严重，试件的硬化阶段曲线较为平缓.试件加载至末期，标距段内断裂瞬间发生，且一裂到底，试件承载力骤降为0.

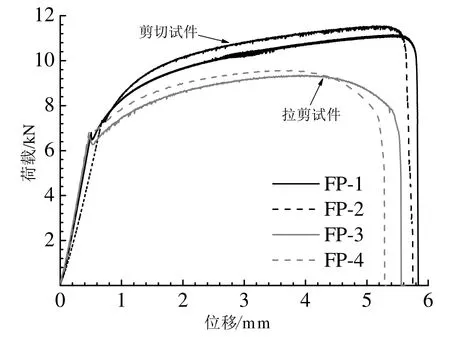
图10 剪切型/拉剪型平板切口试件荷载-位移曲线Fig.10 Load-displacement curves of pure-shear and tensile-shear flat specimens

图11 剪切型/拉剪型平板切口试件断口形态Fig.11 Fracture topography of pure-shear and tensile-shear flat specimens

随后，对各平板切口试件的断口形态进行观察可以发现：剪切型平板试件断口表面与试件轴线呈约15度夹角，断口表面光滑且具有金属光泽(图11(a)）；拉剪型平板试件断口表面与试件轴线夹角约为50度，断口呈适度粗糙状，且具有明显颈缩现象(图11(b))，表明试件发生了延性断裂.

3.4 平板槽口试件试验结果

平板槽口试件的荷载-位移曲线及断口形态如图12及图13所示.从图中可以看出，切口尺寸对平板槽口试件的承载力及延性同样具有明显的影响.平板槽口试件的屈服与极限荷载随着槽口半径的减小而升高（槽口半径R=10、3、1 mm试件的屈服荷载分别为50.7 kN、52.8 kN、75.3 kN，极限荷载分别为67 kN、72 kN、93 kN），延性则随着切口半径的减小而降低（槽口半径R=10、3、1 mm试件断裂时刻的位移分别约为1.27 mm、0.91 mm、0.68 mm）.试件加载末期，裂纹首先在试件槽口中部（平面应变状态区）出现，随后裂纹沿着槽口两边一裂到底（平面应力状态区）.经观测，平板槽口试件断口也呈“杯锥型”形态（见图13）.

依据Bridgman公式[3]，平板槽口试件槽口根部最小截面处的平均断裂应变可以表示为如下形式：

式中t0为试件槽口根部初始厚度，tf为槽口根部断裂时刻厚度.根据公式（11）所得各平板槽口试件平均断裂应变见表1.

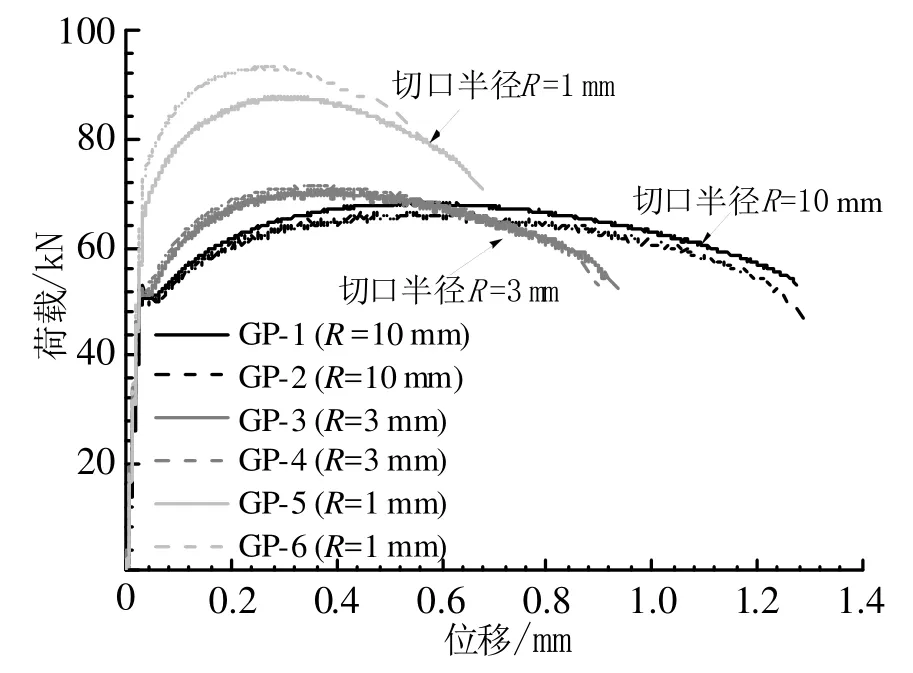
图12 平板槽口试件荷载-位移曲线Fig.12 Load-displacement curves of flat grooved plate specimens

图13 平板槽口试件断口形态Fig.13 Fracture topography for flat grooved plate specimens

3.5 试验结果分析及讨论

将本次试验的主要结果列于表1当中，以便进行系统的比较分析.通过对比表1中的结果，可以发现切口的几何尺寸及应力三轴度是影响切口试件承载力及延性的决定性因素.结构钢材的极限荷载及断裂荷载随着切口锐度及应力三轴度的提升显著升高，延性（颈缩面积及断裂应变）则随着切口锐度及应力三轴度的提升明显下降.因此，在实际工程当中应避免锐型切口的出现.

4 Rice-Tracey延性断裂准则校准

Rice与Tracey[4]曾对静水拉力作用下的微孔扩张模型进行了理论分析，并提出了一个指数型的断裂准则，该准则可以表示为如下形式：

式中C1与C2分别为材料常数.该准则目前被广泛应用于钢结构的断裂预测分析当中.

为了校准Q460D钢材的Rice-Tracey断裂模型，本文将表1中切口圆棒试件及平板槽口试件所得的应力三轴度及断裂应变数据点绘制于如下的图14当中，并采用数据分析软件Origin对这些数据点进行了二维非线性曲线拟合.拟合过程中，采用“最小卡方残差”法来寻找与表1中的数据点最为吻合的拟合曲线.拟合数据点与输入数据点的卡方残差可以表示为：

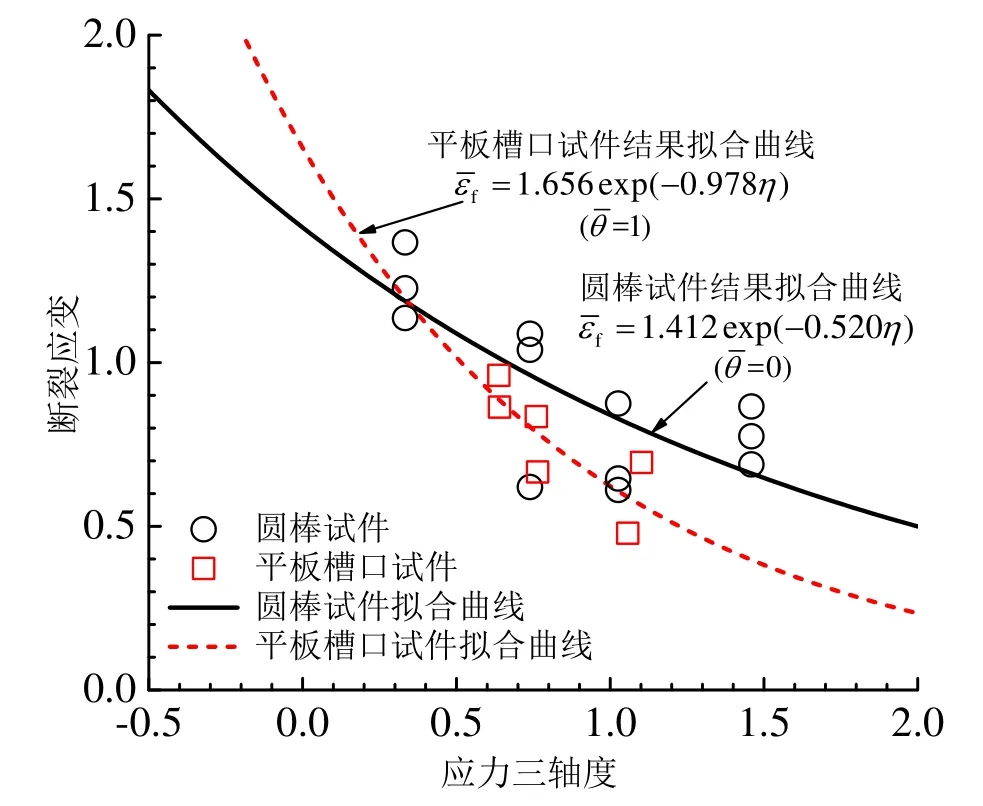
图14 Rice-Tracey断裂准则校准曲线Fig.14 Calibrated fracture curves of Rice-Tracey fracture criterion

图14分别显示了利用圆棒试件与平板槽口试件数据结果拟合得到的Rice-Tracey断裂曲线.其中，利用圆棒试件数据点校准得的断裂曲线表达式为：，利用平板槽口试件数据点校准得到的断裂界限表达式为.从图14中可以发现，在相同Lode角状态下，Rice-Tracey断裂准则可以准确地捕捉材料因应力三轴度升高引起的延性下降趋势.Q460D钢的延性随着应力三轴度的升高基本呈指数形式下降.

5 Q460D结构钢材微观断裂机制分析

为了进一步考察应力状态对Q460D结构钢材微观断裂机制的影响，本文对各切口试件的断口表面进行了电镜扫描分析.各类型切口试件的电镜扫描结果如图15所示.

图15的电镜扫描结果表明，Q460D钢在不同应力状态下呈现出完全不同的微观断裂机制.在拉伸应力状态下（切口圆棒试件及平板槽口试件），试件断口表面呈现出典型的“微孔型”断裂机制.断口中心部位第二相刚性颗粒处出现了大量明显的等轴韧窝.断口表面外围沿着剪应力最大的方向形成“剪切唇”.在纯剪切应力状态下（剪切型平板切口试件），试件断口表面呈现出典型的“剪切型”断裂机制.此时断口表面光滑平整且具有光泽.断口表面沿着最大剪应力方向出现了类似解理型的层状台阶.在拉剪复合应力状态下（拉剪型平板切口试件），试件断口断裂机制介于“微孔型”与“剪切型”二者之间，试件断口表面上因静水拉力形成的形核微孔沿着剪应力方向被拉长，形成椭圆形及抛物线形孔洞.该结果为进一步提出合理的断裂准则提供物理依据.

图15 各切口试件断口电镜扫描结果Fig.15 Observation Results from SEM (Scanning Electron Microscope)

6 结论

本文对国产Q460D高强度结构钢材静力状态下的断裂性能进行了研究.分别对切口圆棒试件、剪切型及拉剪型平板切口试件、平板槽口试件进行了静力断裂试验，并利用扫描式电子显微镜对各切口试件的断口表面进行了观察分析，考察了切口尺寸与应力状态对钢材延性及微观断裂机制的影响，并利用所得试验数据对Rice-Tracey断裂准则进行了校准，所得结论如下：

(1)切口尺寸对Q460D钢的承载力及延性具有明显的影响，切口试件的屈服荷载及极限荷载随着切口锐度的增加逐步提升，延性则随着切口锐度的增加显著下降.因此，实际工程当中应避免锐型切口的出现.

(2)Q460D钢的断裂应变取决于钢材所处应力状态.Q460D钢的断裂应变随着应力三轴度的升高呈指数形式下降.不同Lode角参数状态下，钢材的断裂应变具有不同的下降趋势.Rice-Tracey断裂准则可以准确的预测Q460D钢在相同Lode角状态下的延性下降趋势.

(3)Q460D结构钢材在不同应力状态下呈现出不同的微观断裂机制.在拉伸应力状态下，Q460D钢呈现出典型的“微孔型”断裂机制；在纯剪切应力状态下，Q460D钢呈现出类似于解理似的层状平滑断裂机制；在拉剪复合应力状态下，Q460D钢呈现出“复合微孔型”断裂机制.

References

[1]周晖,王元清,石永久,等.基于微观机理的梁柱节点焊接细节断裂分析[J].工程力学,2015(5): 37-50.ZHOU Hui,WANG Yuanqing,SHI Yongjiu,et al.Fracture analyses of welded details in beam-to-column connections using micromechanics-based models[J].Engineering Mechanics,2015(5): 37-50.

[2]李国强,王彦博,陈素文,等.高强度结构钢研究现状及其在抗震设防区应用问题[J].建筑结构学报,2013,34(1): 1-13.LI Guoqiang,WANG Yanbo,CHEN Suwen,et al.State-of-the-art on research of high strength structural steels and key issues of using high strength steels in seismic structures[J].Journal of Building Structures,2013,34(1): 1-13.

[3]BRIDGMAN P W.Studies in large plastic flow and fracture[M].New York: McGraw-Hill,1952.

[4]RICE J R,TRACEY D M.On the ductile enlargement of voids in triaxial stress fields[J].Journal of the Mechanics and Physics of Solids,1969,17(3): 201-217.

[5]HANCOCK J W,MACKENZIE A C.On the mechanisms of ductile failure in high-strength steels subjected to multi-axial stress-states[J].Journal of the Mechanics &Physics of Solids,1976,24(2/3): 147-160.

[6]GURSON A L.Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I-Yield Criteria and Flow Rules for Porous Ductile Media[J].Journal of Engineering Materials &Technology,1977,99(1): 2-15.

[7]NEEDLEMAN A,TVERGAARD V.An analysis of ductile rupture in notched bars[J].Journal of the Mechanics &Physics of Solids,1984,32(6): 461-490.

[8]BAI Y,WIERZBICKI T.A new model of metal plasticity and fracture with pressure and lode dependence[J].International Journal of Plasticity,2008,24(6): 1071-1096.

[9]BAI Y,WIERZBICKI T.Application of extended Mohr-Coulomb criterion to ductile fracture[J].International Journal of Fracture,2010,161(1): 1-20.

[10]CAO T S,GAILLAC A,MONTMITONNET P,et al.Identification methodology and comparison of phenomenological ductile damage models via hybrid numerical-experimental analysis of fracture experiments conducted on a zirconium alloy[J].International Journal of Solids and Structures,2013,50(24): 3984-3999.

[11]BAI Y,WIERZBICKI T.A comparative study of three groups of ductile fracture loci in the 3D space[J].Engineering Fracture Mechanics,2015,135: 147-167.

[12]全国钢标准化技术委员会.GB/T 1591-2008.低合金高强度结构钢[S].北京: 中国标准出版社,2008.The Technical Committee on Steel of Standardization Committee of China.GB/T 1591-2008.High strength low alloy structural steels[S].Beijing: China Standard Press,2008.

[13]ASTM International.ASTM International.Standard test methods for tension testing of metallic materials: ASTM E8/E8M-11[S].West Conshohocken PA: ASTM International,2011.

[14]BAO Y,WIERZBICKI T.On fracture locus in the equivalent strain and stress triaxiality space[J].International Journal of Mechanical Sciences,2004,46(1): 81-98.