OFDM-WLAN系统互相关超分辨TOA估计

崔维嘉，陆杰青，裴喜龙，范立岩

(1.解放军信息工程大学 信息系统工程学院，河南 郑州450001；

2.解放军信息工程大学 导航与空天目标工程学院，河南 郑州450001)

Foundation Item:Chinese National Programs for High Technology Research and Development (No. 2012AA01A505,No. 2012AA01A502)

摘　要：在正交频分复用无线局域网系统的室内场景下，针对单快拍多重信号分类的超分辨到达时间估计由于多径数估计不准确导致的到达时间估计误差偏大的问题，提出了一种未知多径数的互相关超分辨到达时间估计算法。该算法根据正交频分复用无线局域网系统的物理层协议数据单元的特点，考虑到前导码中相邻两个长正交频分复用符号的信道不变性和噪声的不相关性，首先利用两个长正交频分复用符号估计两组信道频域响应，然后，采用前后向频域平滑的方法，求两组信道频域响应的互相关矩阵，进而用所求互相关矩阵逆的高次幂近似噪声特征矩阵的乘积，最后构造伪谱函数并进行谱峰搜索，从而实现到达时间的估计。仿真结果表明，该算法估计精度高，且对噪声不敏感，具有较好的鲁棒性。

关键词：正交频分复用；超分辨；互相关；到达时间

doi:10.3969/j.issn.1002-0802.2015.06.003

OFDM-WLAN系统互相关超分辨TOA估计

崔维嘉1，陆杰青1，裴喜龙1，范立岩2

(1.解放军信息工程大学 信息系统工程学院，河南 郑州450001；

2.解放军信息工程大学 导航与空天目标工程学院，河南 郑州450001)

Foundation Item:Chinese National Programs for High Technology Research and Development (No. 2012AA01A505,No. 2012AA01A502)

摘要：在正交频分复用无线局域网系统的室内场景下，针对单快拍多重信号分类的超分辨到达时间估计由于多径数估计不准确导致的到达时间估计误差偏大的问题，提出了一种未知多径数的互相关超分辨到达时间估计算法。该算法根据正交频分复用无线局域网系统的物理层协议数据单元的特点，考虑到前导码中相邻两个长正交频分复用符号的信道不变性和噪声的不相关性，首先利用两个长正交频分复用符号估计两组信道频域响应，然后，采用前后向频域平滑的方法，求两组信道频域响应的互相关矩阵，进而用所求互相关矩阵逆的高次幂近似噪声特征矩阵的乘积，最后构造伪谱函数并进行谱峰搜索，从而实现到达时间的估计。仿真结果表明，该算法估计精度高，且对噪声不敏感，具有较好的鲁棒性。

关键词：正交频分复用；超分辨；互相关；到达时间

doi:10.3969/j.issn.1002-0802.2015.06.003

收稿日期：2015-01-07；修回日期：2015-04-19Received date:2015-01-07；Revised date：2015-04-19

基金项目：国家高技术研究发展计划(863计划) (No.2012AA01A505，No.2012AA01A502)

中图分类号：TN92

文献标志码：码：A

文章编号：号：1002-0802(2015)06-0642-06

Abstract：In the indoor WLAN(Wireless Local Area Networks) using DFDM(Orthogonal Frequency Division Multiplexing),TOA(Time of Arrival) can be estimated via MUSIC(Multiple Signal Classification) algorithm based on a single snapshot data, and aiming at the big estimation errors resulted from the incorrect estimation of multipath number, a super-resolution TOA algorithm based on co-correlation under the condition of unknown number of multipath is proposed. This algorithm makes full use of the properties of physical layer protocol data unit in OFDM-WLAN system. The invariance property of channels and the uncorrelated property of random noise are taken into consideration between two OFDM symbols in preamble. First of all, two sets of channel response in frequency domain are estimated by using two long OFDM symbols. Then, cross-correlation matrix of two sets of channel response in frequency domain is estimated by using forward and backward frequency smooths. And the inverse of cross-correlation matrix high frequency power is similar to the product of two matrices composed of noise eigenvectors. Finally, the pseudo-spectral function is constructed and used to search spectrum peak, thus to realize the estimation of TOA. Simulation results show that the proposed algorithm , with high estimation precision, and being insensitive to noise, is of good robustness.

作者简介：

Super-Resolution TOA Estimation based on

Co-Correlation for OFDM-WLAN

CUI Wei-jia1，LU Jie-qing1，PEI Xi-long1, FAN Li-yan2

(1.School of Information Systems Engineering, PLA Information Engineering University,

Zhengzhou Henan 450001,China;2.School of Navigation and Aerospace Object

Engineering, PLA Information Engineering University, Zhengzhou Henan 450001,China)

Key words：OFDM; super resolution; co-correlation; time of arrival

0引言

正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术具有较高的频带利用率，并且可以有效对抗频率选择性衰落[1]。近年来该技术已被应用到长期演进[2](Long Term Evolution,LTE)、全球微波互联接入[3](Worldwide Interoperability for Microwave Access,WiMax)和电气和电子工程师协会(Institute of Electrical and Electronics Engineers,IEEE)802.11[4]无线局域网(Wireless Local Area Network,WLAN)等各个系统。WLAN利用OFDM技术为用户带来了极佳的体验并得到了普及。在定位方面，特别是在卫星定位系统和蜂窝网络定位系统均失效的室内场景下，OFDM-WLAN系统利用现有的基础设施对工作站实施定位具有极大的应用价值。

在基于OFDM-WLAN的定位系统中，到达时间(Time of Arrival,TOA)估计是其中一项重要的研究内容。受系统工作带宽和采样率的限制，传统的TOA估计方法在室内场景下性能较差，文献[5]给出了一种基于子载波相位差的OFDM无线信号TOA估计算法，该算法在高斯白噪声信道中能够提供估计精度高、不模糊范围大的TOA估计，但无法适用于复杂的多径环境。为精确地估计TOA，学者们提出了许多超分辨算法，包括最小范数谱估计算法[6]，多重信号分类(Multiple Signal Classification,MUSIC)算法[7]、传播算子算法(Propagator Method,PM)[8]、求根MUSIC算法[9]、旋转不变技术估计信号参数(Estimation of Signal Parameters via Rotational Invariance Techniques,ESPRIT)算法[10]等。这些超分辨算法通常在大量快拍和较高信噪比的条件下预先对多径数进行估计，然后通过特征分解，最后利用谱峰搜索得到TOA估计。在有限快拍条件下，特别是在单快拍条件下，现有多径数估计算法性能较差，最终导致TOA估计误差较大。超分辨算法通常对信噪比要求较高，在低信噪比环境下，算法性能大幅度下降。另外，这些算法需要特征分解，计算复杂度较高。

针对以上问题，在室内场景下，利用OFDM-WLAN系统的物理层协议数据单元的特点，本文提出一种未知多径数的互相关超分辨TOA估计算法。此算法不需要预先估计多径数和特征分解，在两快拍和低信噪比的条件下，依然能够保持较高的TOA估计精度。

1信号模型

在OFDM-WLAN通信系统中，无线多径信道的冲击响应为：

(1)

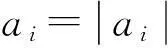
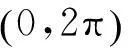
OFDM输入信号的时域表达式为：

0≤t≤T+TG,0≤k≤K-1

(2)

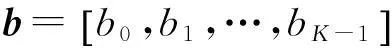
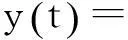
(3)

式中，yk表示第k子载波的接收数据，则：

(4)

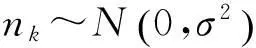
那么，第k个子载波的信道频域响应为：

(5)

信道频域响应估计可以表示为矩阵形式：

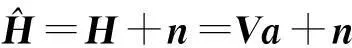
(6)

式中：

2未知多径数的互相关超分辨TOA估计算法

在OFDM-WLAN系统中，物理层协议数据单元包含两个相邻的长OFDM符号，该符号可以估计两组信道频域响应。在室内场景中，工作站的运动速度较慢，相对于两个长OFDM符号周期可以认为是静止的。因此，相邻两个长OFDM符号周期内的信道可以认为是不变的，并且噪声是不相关的。为了提高TOA的估计精度，利用上述特点，本文给出了一种未知多径数的互相关超分辨TOA估计算法。该算法利用两组信道频域响应的互相关抑制噪声，并采用互相关矩阵逆的高次幂来近似噪声特征矩阵的乘积，避免了有限快拍下多径数估计不准确带来的TOA估计误差。

下面首先分析OFDM-WLAN系统中信道频域响应互相关矩阵的特性，并给出两快拍互相关矩阵的估计方法；在此基础上，设计未知多径数的超分辨TOA估计方法；最后给出算法流程与分析。

2.1信道频域响应互相关矩阵的特性

在OFDM-WLAN系统中，物理层协议数据单元以前导码作为开始，如图1所示。它是由10个短OFDM符号和2个长OFDM符号所组成，其中短OFDM符号用于粗时间同步和粗频率同步，长OFDM符号用于信道估计。

图1　前导码结构

在室内场景下，由于一个长OFDM符号周期仅为3.2 μs，多径信道在两个长OFDM符号周期内可以认为不变。利用两个长OFDM符号分别进行信道估计得：

(7)

(8)

(9)

(10)

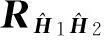
(11)

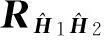
ξ0≥…≥ξLP-1>ξLP=ξLP+1=…=ξK-1=0

(12)

对角矩阵ΣS=diag{ξ0,ξ1,…,ξLP-1}，对角矩阵ΣN=diag{ξLP,ξLP+1,…,ξK-1}=0。信号特征矩阵US=u0,u1,…,uLP-1]的值域空间range(US)称为信号子空间，噪声特征矩阵UN=[uLP,uLP+1,…,uK-1]的值域空间range(UN)称为噪声子空间。

利用噪声间的相互独立性，信道频域响应的互相关技术可以消除噪声，使得子空间估计与噪声无关，从而可以准确估计出信号子空间和噪声子空间。在有限快拍时，噪声无法完全消除，但可以得到有效抑制。

2.2两快拍互相关矩阵的估计

在OFDM-WLAN系统中，一个物理帧能估计出两个快拍的信道频域响应。将维数为K的信道频域响应划分为M组维数为L的连续信道频域响应子矢量，并利用频域平滑估计互相关矩阵，如图2所示。

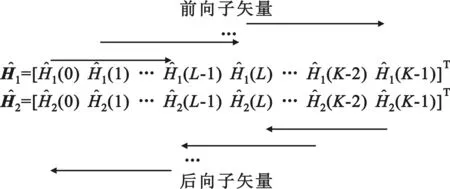
图2　前后向频域平滑

前向频域平滑互相关矩阵可以表示为：

(13)

其中，M=K-L+1，

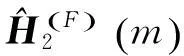
对于有限数据，可以利用后向频域平滑改善互相关矩阵的估计性能。后向频域平滑互相关矩阵可以表示为：

(14)

式中，

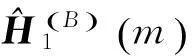
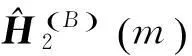
对前、后向频域平滑求平均得互相关矩阵的估计：

(15)

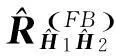
2.3未知多径数的超分辨TOA估计

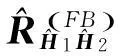
(16)

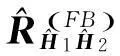
(17)

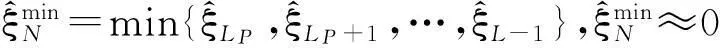
(18)

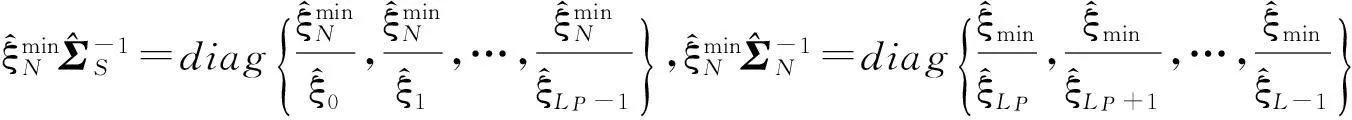
(19)

(21)

构造互相关伪谱：

(21)

2.4算法流程及分析

由以上推导与分析，所提算法的流程如图3所示，并可以归纳如下：

Step1:利用OFDM-WLAN系统物理层协议。

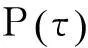
Step5:利用谱峰搜索，估计τ0。

图3　未知多径数的互相关超分辨TOA估计算法流程

通过对比传统的MUSIC超分辨TOA估计算法可以发现，所提算法具有如下优势：

传统算法利用多径数LP划分噪声子空间。在单快拍或者两快拍时，多径数估计算法失效。所提算法无需多径数估计，从而避免了这项误差。

(2)算法采用互相关的方法抑制了噪声。

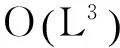
3仿真实验

本节将利用仿真来验证所提算法的性能。仿真条件设置如下：假设信号强度不变，信道参数利用WINNERA1场景模型[11]产生，接入点与工作站之间的距离为50m。传统MUSIC算法的多径数估计采用信息论方法最小描述长度(MinimumDescriptionLength，MDL)算法和赤池信息量准则(AkaikeInformationCriterion，AIC)算法。OFDM信道估计的相关参数设置，如表1所示。

表1　OFDM信道估计相关参数设置

仿真1：为了考察算法的稳定性，在不同信噪比下，通过1 000次Monte Carlo实验计算MDL-MUSIC、AIC-MUSIC、真实多径数MUSIC和m=5时的本文算法TOA估计误差绝对值的均值和均方根误差(RMSE，Root Mean Square Error)：

(22)

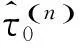
图4和图5分别给出了误差均值的绝对值和RMSE随信噪比的变化情况。从图中可以看出，由于信号强度不变，随着信噪比的降低，即噪声的增强，算法的误差均值的绝对值与RMSE对噪声不敏感。随着信噪比的提高，本文算法与真实多径数MUSIC算法的误差绝对值的大致相当。本文算法的RMSE性能明显优于MDL-MUSIC和AIC-MUSIC算法，并接近真实多径数MUSIC算法的RMSE性能。这是因为算法避免了多径数估计引入的子空间估计误差，并用互相关矩阵逆的高次幂逼近噪声特征矩阵的乘积，算法性能逼近真实多径数MUSIC算法。

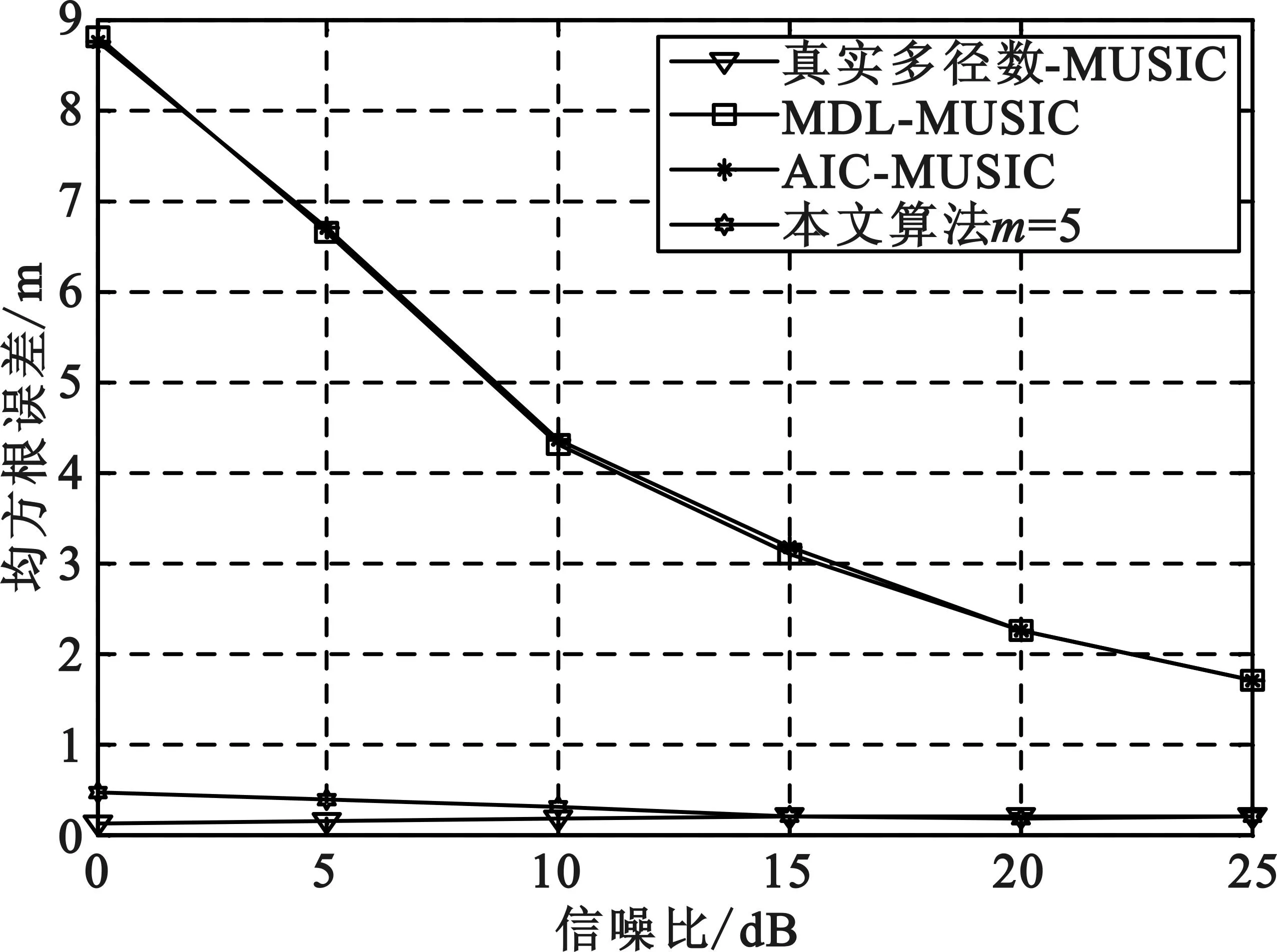
图4误差均值绝对值随信噪比的变化

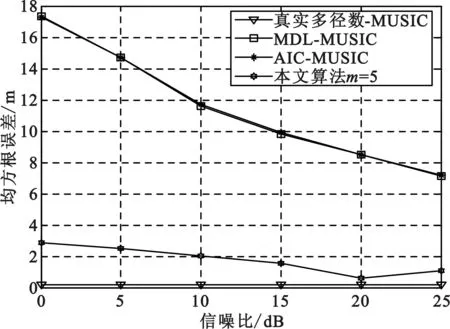
图5　均方根误差随信噪比的变化

仿真2：为了考察算法的TOA估计精度，在信噪比为0 dB下，通过1 000次Monte Carlo实验分别计算MDL-MUSIC、AIC-MUSIC和本文算法TOA估计的累积分布函数(Cumulative Distribution Function，CDF)。

图6和图7分别给出了本文算法与MDL-MUSIC算法和AIC-MUSIC算法在0 dB时的CDF对比曲线。可以看出，本文算法性能明显优于MUSIC算法。这是因为在有限快拍条件下，本文算法利用相关抑制了噪声，并且无需多径数估计，从而避免了由于有限快拍所导致的子空间发散。

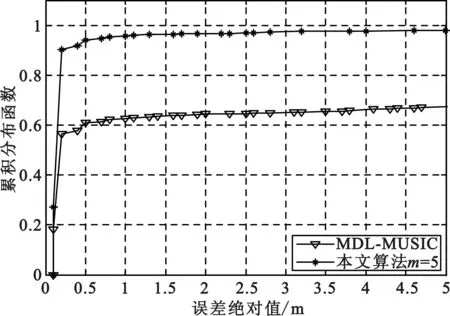
图6　信噪比为0 dB时本文算法与MDL-MUSIC

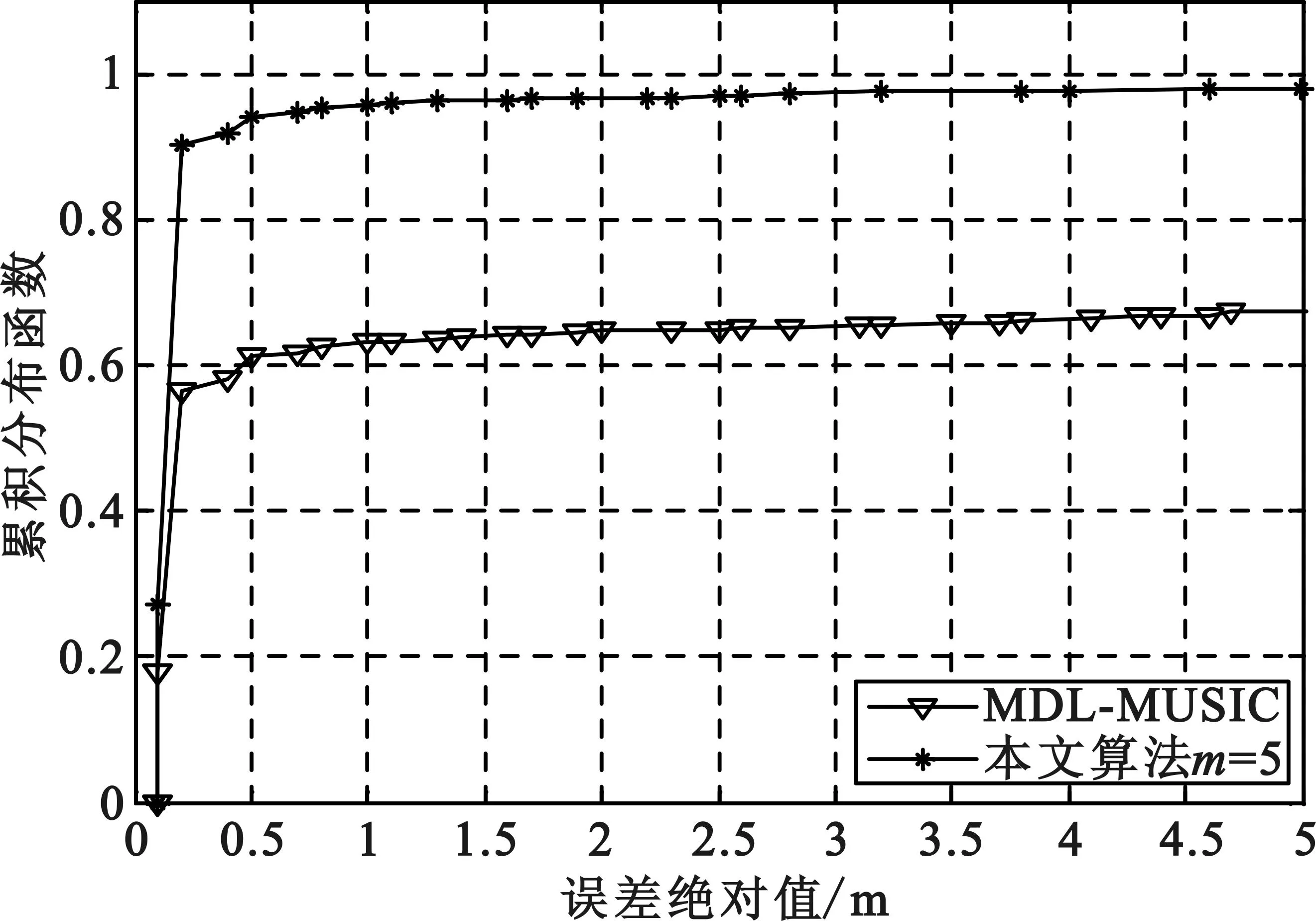
图7　信噪比为0 dB时本文算法与AIC-MUSIC

仿真3：为了考察算法TOA估计精度随信噪比的变化，通过1 000次Monte Carlo实验分别计算误差绝对值小于3 m的概率，仿真结果如图 8所示。可以看出，随着信噪比的提高，本文算法误差绝对值小于3 m的概率明显优于MDL-MUSIC、AIC-MUSIC，并对噪声不敏感。

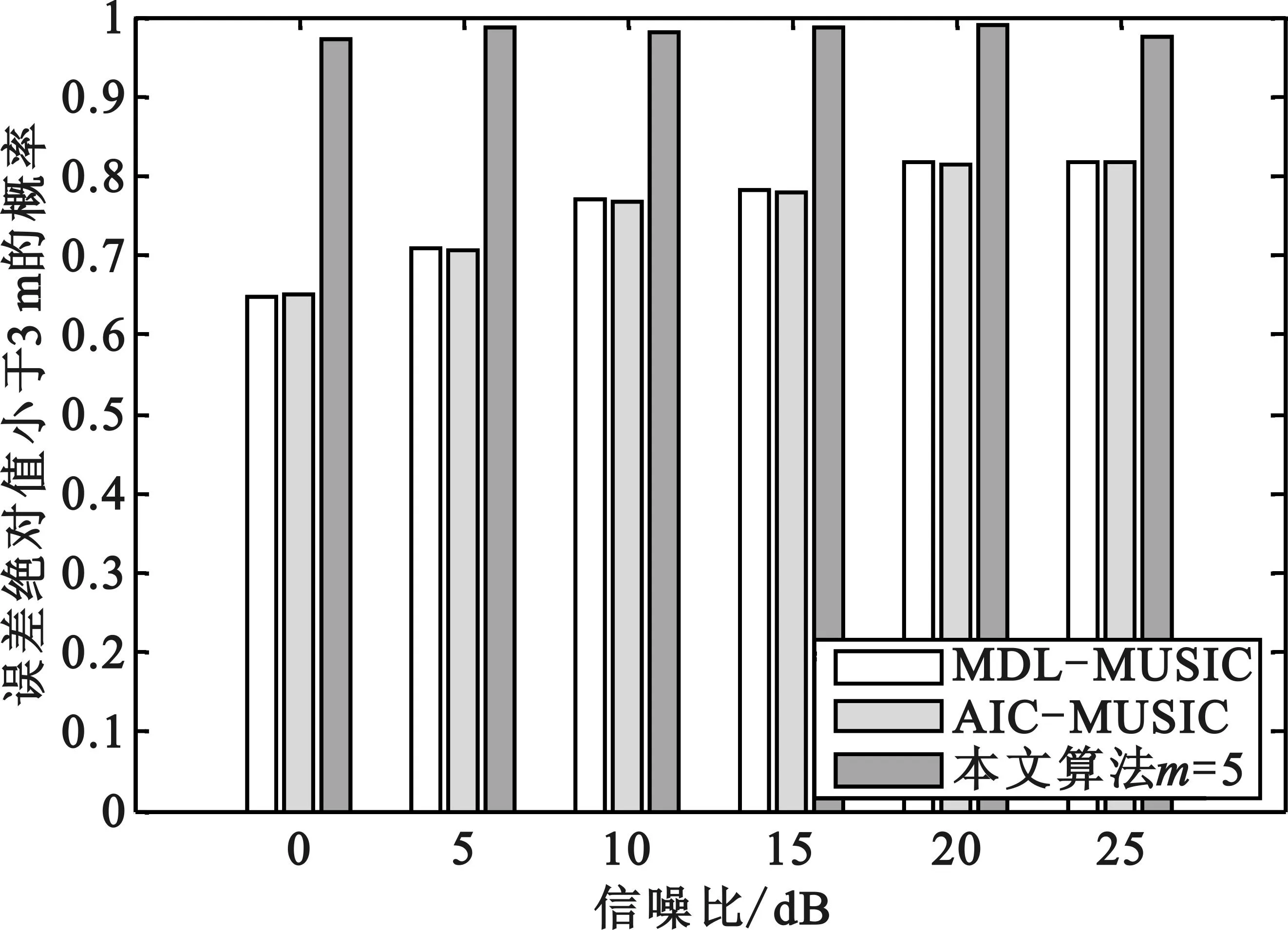
图8　不同信噪比下误差绝对值小于3 m的概率

4结语

本文针对OFDM-WLAN系统的室内场景，给出了一种未知多径数的互相关超分辨TOA估计算法，并做出了相应的理论公式推导和仿真实验。对于室内场景，由于前导码中相邻两个长OFDM符号周期内的信道和噪声分别具有不变性和不相关性，本文对两组信道频域响应求互相关矩阵可以有效抑制噪声，并利用互相关矩阵逆的高次幂逼近噪声特征矢量矩阵的乘积，从而避免了多径数估计误差对TOA估计性能的影响。仿真结果表明，本文算法的TOA估计性能明显优于MDL-MUSIC算法和AIC-MUSIC算法，具有良好的实用价值。

参考文献：

[1]杨宏周,杨灿美.一种降低OFDM系统PAPR的参数化整形脉冲[J]. 通信技术,2014, 47(05):1-2.

YANG Hong-zhou, YANG Can-mei. A Parametric Shaping Pulse for PAPR Reduction in OFDM System [J]. Communications Technology, 2014, 47(05):1-2.

[2]AJEY S, SRIVALLI B, RANGARAJ G V. OnPerformance of MIMO-OFDM based LTE Systems[C]//Wireless Communication and Sensor Computing, 2010. ICWCSC 2010. International Conference on. IEEE,2010:1-5.

[3]ZHAO X, CUI L. ANew Frame Synchronization Algorithm for OFDM WiMAX System in Simulink[C]//Computer Science and Network Technology (ICCSNT), 2011 International Conference on. IEEE,2011,4:2321-2325.

[4]ARRUE N, VELEZ I, SEVILLANO J F，et al. Two Coarse Frequency Acquisition Algorithms for OFDM based IEEE 802.11 standards[J]. Consumer Electronics, IEEE Transactions on, 2007,53(1): 33-38.

[5]倪浩. OFDM无线系统中的TOA估计技术研究[D]. 西安:西安电子科技大学, 2010.

NI Hao.Research on TOA Estimation Technologies in OFDM Wireless Systems[D].Xi′an:Xidian University,2010.

[6]李晶, 裴亮, 曹茂永.一种用于多径环境的超分辨率TOA 定位算法[J]. 电波科学学报，2006, 21(05): 771-776.

LI Jing, PEI Liang, CAO Mao-yong. Super-Resolution TOA Algorithm in Multi-path Environments[J]. Chinese Journal of Radio Science,2006,21(5):771-776.

[7]LI X, MA X, YAN S,et al. Super-Resolution Time Delay Estimation for Narrowband Signal[J].IET Radar, Sonar & Navigation，2012, 6(08): 781-787.

[8]JIANG H, CAO F, DING R. PropagatorMethod-based TOA Estimation for UWB Indoor Environment in the Presence of Correlated Fading Amplitudes[C]//Circuits and Systems for Communications,2008. ICCSC 2008. 4th IEEE International Conference on. IEEE,2008:535-538.

[9]王方秋, 张小飞, 汪飞. IR-UWB系统中基于root-MUSIC算法的TOA和DOA联合估计[J]. 通信学报,2014, 35(02): 137-145.

WANG Fang-qiu, ZHANG Xiao-fei, WANG Fei. Root-MUSIC-based Joint TOA and DOA Estimation in IR-UWB [J]. Journal on Communications, 2014, 35(02): 137-145.

[10]OH D, KIM S, YOON SH,et al. Two-Dimensional ESPRIT-like Shift-Invariant TOA Estimation Algorithm using Multi-Band Chirp Signals Robust to Carrier Frequency Offset[J]. Wireless Communications, IEEE Transactions on: 2013, 12(07): 3130-3139.

[11]BULTITUDE Y J, RAUTIAINEN T. IST-4-027756 WINNER II D1.1.2 V1.2 WINNER II Channel Models[J].2007.

崔维嘉(1976—)，男，博士，讲师，主要研究方向为无线与移动通信技术、无线定位技术；

陆杰青(1975—)，男，硕士，讲师，主要研究方向为通信技术；

裴喜龙(1978—)，男，硕士，讲师，主要研究方向为无线定位技术；

范立岩(1990—)，男，硕士研究生，主要研究方向为室内外无缝定位技术。