用户约束下的三维动画模型序列一致性分割

潘　翔，童伟淮，许洪涛，汪志星

(1.浙江工业大学 计算机科学与技术学院，浙江 杭州 310023；2.郑州市人力资源与社会保障局 数据管理中心，河南 郑州 450006)



用户约束下的三维动画模型序列一致性分割

潘翔1，童伟淮1，许洪涛2，汪志星1

(1.浙江工业大学 计算机科学与技术学院，浙江 杭州 310023；2.郑州市人力资源与社会保障局 数据管理中心，河南 郑州 450006)

摘要：针对三维动画模型分割不一致问题，提出基于三维数据对齐技术的三维动画模型交互式分割算法，得到层次结构一致的分割结果.算法首先对首帧进行交互标记；然后通过主向量分析完成三维模型不同帧之间的对齐，自动把用户标记映射到其他模型；最后以方向夹角为基础，设计图割算法，根据模型关节所具有的曲率特征进行边界优化，得到满意的分割结果.实验结果表明，算法针对人造动画模型序列和多视图三维重建动画序列都能够得到一致性分割结果，验证了算法的有效性.最后和已有典型分割方法进行比较分析，可以发现算法能够有效地提高分割质量.

关键词：三维动画模型；交互式分割；三维模型对齐；图割

在计算机视觉和计算机图形学领域，分割技术得到了广泛的运用，例如物体识别[1]、三维重建[2]、网格参数化[3]、三维模型检索[4].因此，三维模型分割已经引起了越来越多研究人员的兴趣.

近年来，研究人员针对分割问题展开了大量的研究，使用了一系列特征，如分水岭[5]、聚类[6]、形状直径函数(SDF)[7]和热核信号(HKS)[8].协同分割结合了多个特征对模型进行分割[9-10].但这类纯粹按照几何的划分方式，并不能实时满足用户需求.因而，研究人员又提出了点交互[11]和草图交互[12-13]分割策略，通过反馈来提高分割效果[14].然而很少有学者关注模型序列分割，动画模型序列通常具有大量姿态各异的帧，通过几何特性或交互式分割都只针对单模型，不能将已有的前驱帧分割知识映射至后续帧，从而造成分割结果不一致.有学者试图通过监督学习的方法，但这些方法分割结果固定，用户无法自定义修改，有些训练时间长，用户交互性差[1].针对上述问题，提出了面向三维动画模型序列的一种交互式方法.用户只需在首帧上指定一些简单的交互标记就可以得到整个序列一致的分割结果.整个算法采用从粗到精的分割策略.首先，算法通过模型对齐技术得到外部特征点，并得到粗分割结果.然后，采用图割技术对粗分割进行优化，得到光滑的分割边界.在实验中，通过不同的三维动画模型序列对算法进行验证发现，对于不同的模型序列，算法都能够得到一致性分割结果，显著提高分割质量.

1算法概述

算法是通过用户交互控制三维动画模型序列分割结果.通常动画模型由一个刚性主体部分和一些外在子部分组成.因此，分割任务主要是提取这些子部分.整个算法流程如图1所示.首先，使用鼠标点击作为交互，用户将会在第一个网格的切割边界附近放置一些标志.然后，算法可以根据网格中的这些标志进行分割输出.注意各部分可以由两种标志定义：外在点和连接点.外点在远离中央的那些部分，连接点位于两部分连接处.整个算法可以分三个步骤执行；首先，通过多维尺度变换实现模型对齐；其次，根据对齐结果检测得到模型的特征点；最后，使用一个两阶段策略得到分割结果.第一阶段是利用外部点和长度进行粗分割.第二阶段是通过图进行优化分割.

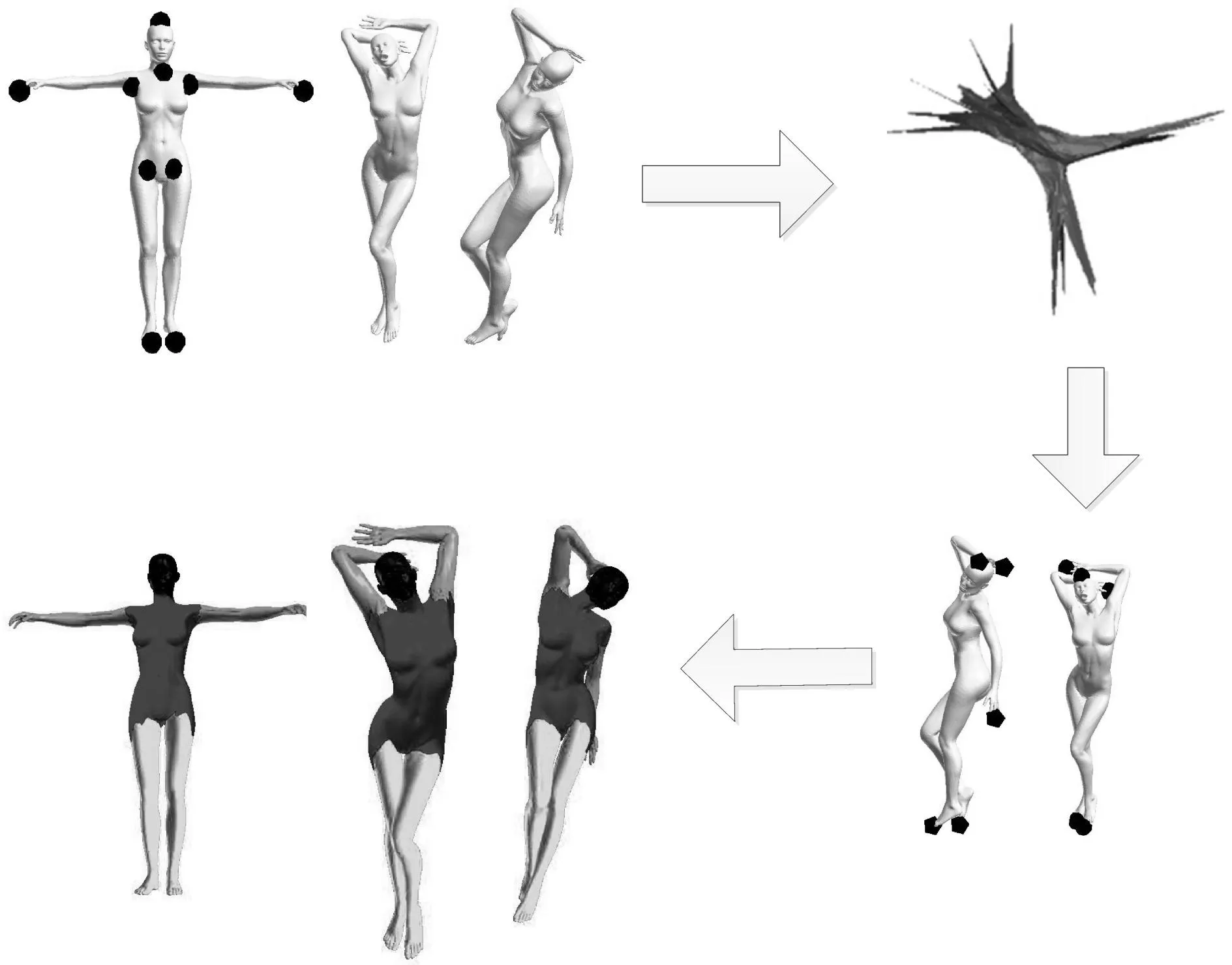
图1　算法流程图Fig.1　Flowchart of proposed algorithm

2算法细节

讨论如何具体实现上述算法流程.为了简化描述，给出了一些常见的分割定义.为了不失一般性，假设三维形状采用三角网格表示.其他的三维形状表示，如NURBS曲面，元球，细分曲面和体积，可以很容易地转换成三角形网格.对于一个三维网格，它的顶点集合和面集合分别为V和F，顶点数量分别为Nv和Nf.对于任何两个顶点vi和vj，其测地距离为gd(vi,vj).类似的，两个面之间的测地距离为gd(fi,fj).分割任务是根据用户交互定义，将网格序列分割成相同结构的子部分S1,…,Si,…Sj,…，SK(K为子部分数量).这里每个部分包含一组连接的面.对于每一个部分Sj，它有一个长度Lj.长度是从外点到连接点的测地距离.所有子部分满足以下条件：

(1)

2.1MDS和局部特征相结合的外部点提取

对于其他未被标记的网格，注意到两个三维网格在运动过程中具有不同的姿势，而外部点保持稳定.采用对齐算法提取外部点.首先，使用MDS将两个网格转化为规范的姿势[15].在这里，可以通过顶点之间的测地距离定义MDS变换所需的矩阵.因此，目标函数可以定义为

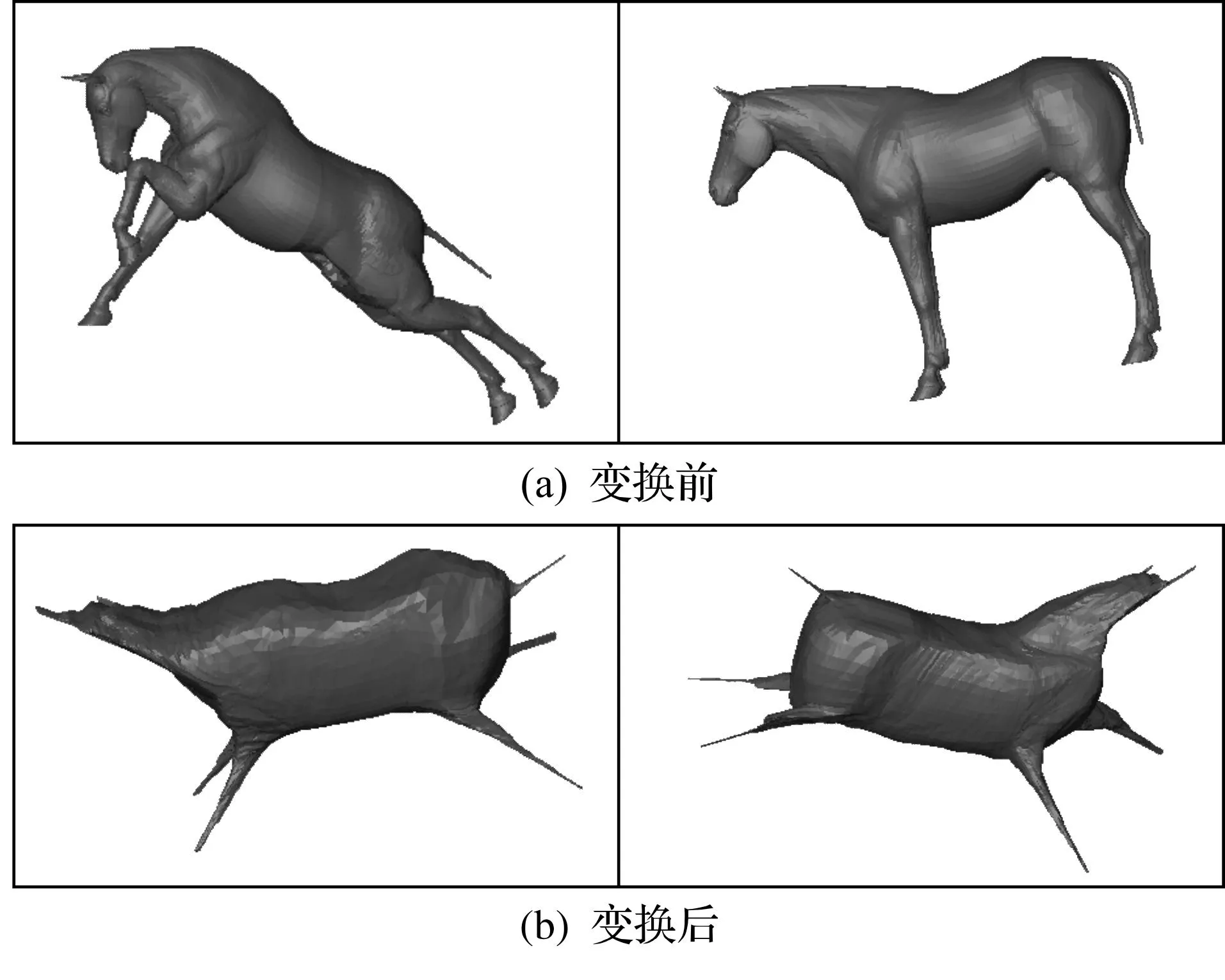
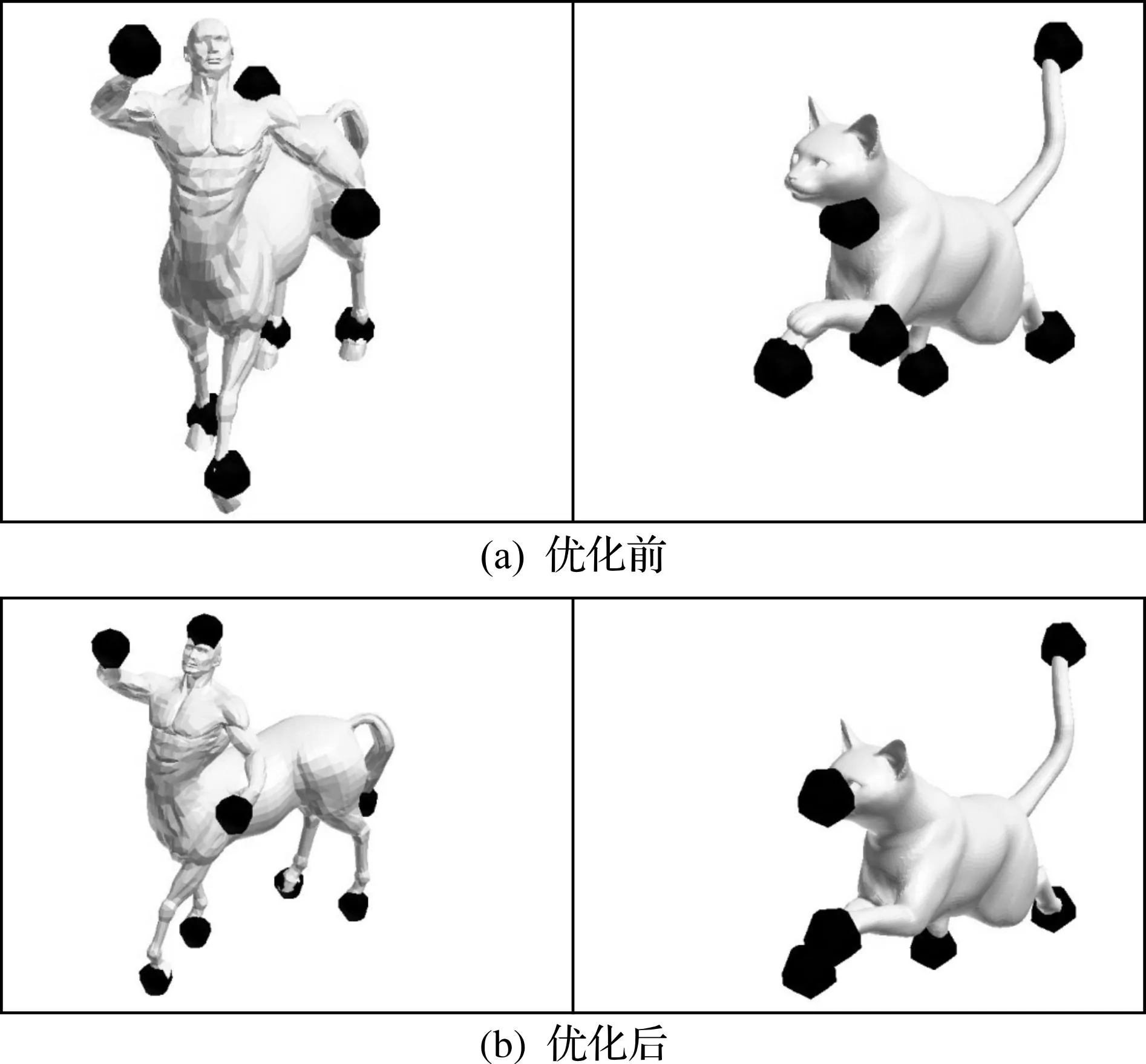
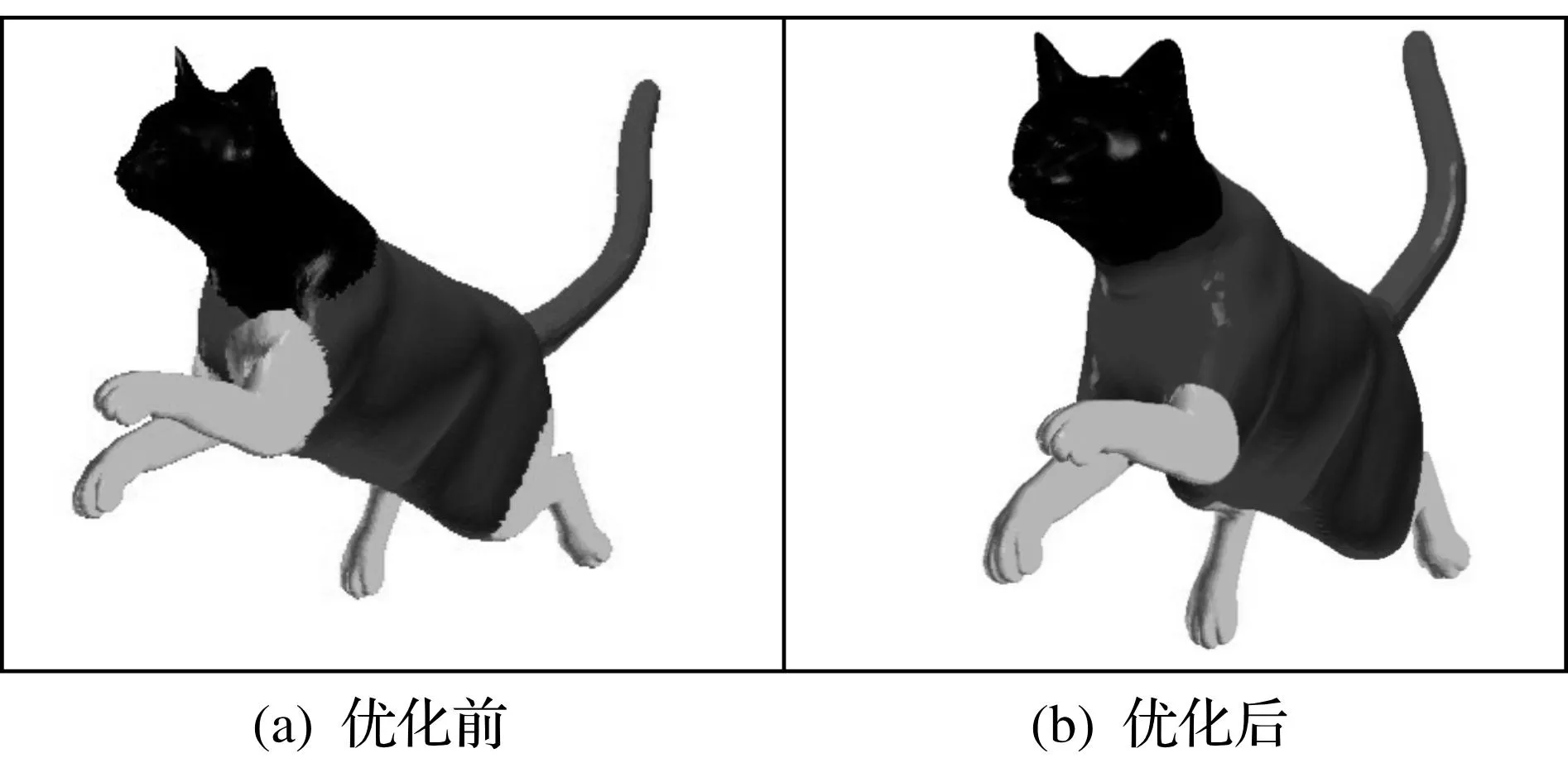
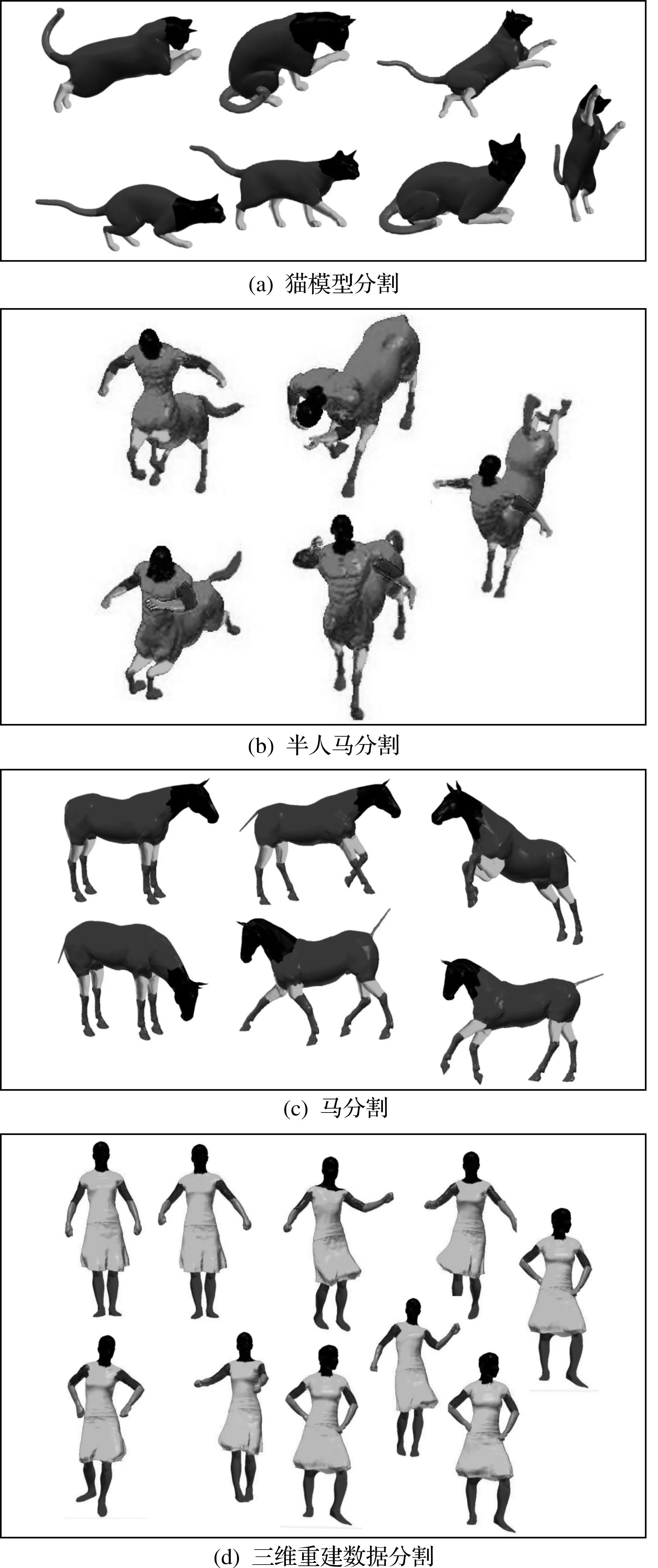
S(V)=min∑i

(2)

式中di，j为任意两个顶点之间的欧氏距离.上述函数是用欧氏距离来逼近测地距离.图2给出了两个不同姿态的马模型经过MDS变换的结果.可以发现两个马模型的姿态已经变得一致.

图2　不同姿态通过MDS变换得到的结果Fig.2　The MDS results in different pose models

通过MDS变换后，可以使用主向量分析(PCA)对齐两个网格.主向量分析构建一个旋转不变的协方差矩阵.但是，PCA因为二义性会导致错误对齐.例如，PCA可能把一匹马的尾巴对齐到其它马的头.这种情况下，可以通过两个点集的最小欧氏距离来解决.PCA可以在3D空间输出27种可能的对齐方向.因此，可以计算两个网格对齐后的欧氏距离.最后，选择最小距离方向作为最好的对齐结果.两个点集的欧氏距离计算式为

(3)

式中VA和VB分别为两个网格变化后的点集.通过上述目标函数，可以在目标网中为源网格的每个顶点找到和它最接近的点.通过最优对齐，在未标记网格上找到相应的外点.这里采用fi,e代表Si的外部点.考虑到对齐的准确性，算法会执行一个后处理.后处理的思想是将检测到的标志尽可能远地远离中心点.中央点计算式为

(4)

在得到中心点以后，采用下式完成外点位置的更新式为

fi,e={fq|minfw∈E∪fcgd(fq,fw),

maxfq∈Fgd(fq,fc)>gd(fi,e,fc)}

(5)

式中E为外部点集.上述方程是最大化其他指定外部点到中心点的最小距离.图3显示了一些处理前后结果.在后处理之前，一些通过PCA得到的外点在中间区域.通过优化后，外点的精度大大提高.

图3　优化前后的外点位置对比Fig.3　Comparison of unrefined and refined positions of external points

2.2粗分割

在检测到外部点基础上，粗分割可以结合子部分长度得到.注意到这些不同姿势的网格有类似的测地距离.因此，对于三维序列的每个网格，其子部分的长度几乎保持不变.在这种方式中，可以得到一个子部分：

Si={fj|gd(fi,e,fj)

(6)

式中Li为通过标注网格得到的长度.类似的，可以得到其他子部分.

2.3边界优化

粗分割结果可以得到三维网格结构，然而分割边界质量较差.因此，我们需要优化来消除锯齿边.通常一个好的分割应尽可能地通过凹形区域.凹区域可以用曲率特征来判断.在这里，采用图割来优化边界.

图割通过最大流算法实现[16]，两个相邻的部分之间执行图割需要三个主要步骤：首先，将切割边界附件的面片被指定为模糊区域，同时将该区域构建为图结构，算法的实质就是是重新分配这些面片，最终得到一个光滑边界；其次，计算图中边得权重，笔者根据两个相邻面片的夹角定义计算了边的权重公式，最后，添加虚拟的源点和汇点及边的代价权重得到最终的路径，该路径映射回模型表面即为分割边界.

2.3.1构建模糊区域

模糊区域包含的面与外点的测地距离小于预定义的阈值α，其面的集合为

(7)

式中α设定为0.2.

2.3.2定义图的边代价

用二面片夹角定义边代价可以使分割边界具有高度凹性，εij为面fi和fj的二面角，二面角的共同边代价定义为

(8)

式中：avg(cost(ε))为平均角距离;cost(εij)为归一化因子，定义为

(9)

式中:当夹角为凹时，因子δ等于1，否则等于0.3.

2.3.3求解路径

通过两个虚拟节点，根据外部点和边成本，该算法能沿着凹边对图进行分解.因此，可以从模糊区域求解得到相对光滑的边界.图4显示了优化前后的图割.优化结果可以准确地找到更为光滑的边界.

图4　优化前后对比Fig.4　Comparison of unrefined and refined segmentation

3实验分析

实验环境为英特尔®核心TM双T9300，2.5 GHz和2 G内存，操作系统为Windows XP.在实验中，通过运行不同类型的三维数据算法来验证算法的通用性.实验数据主要包括两部分，一部分来自于TOSCA数据库的人造模型，另外一部分来自于真实重构的运动数据.实验首先对算法的稳定性进行分析，然后把算法和已有典型分割方法进行比较分析，进一步论证算法的有效性.

3.1稳定性分析

首先，在TOSCA数据库的一些人造模型上验证了方法的有效性.该数据库包含了不同序列，包括马、半人半马及猫等.每个序列由一些含不同姿态的三维网格组成.对每个序列，我们首先在第一网格上定义交互标记.然后，去执行算法来得到序列中任意一个模型的分割.图5显示了不同序列的结果.对于猫，只用了12个标记得到了了分割.然而，对半人马和马使用了更多的标记去得到层次分割.

图5　不同三维动画序列的分割结果Fig.5　Segmentation results of different model sequences

为了进一步验证算法的通用性，同时对一个真实重建数据进行实验.被测试的序列是一个跳舞动作，由多台摄像机立体构成得到[17].如图5(d)所示，这个算法能够得到非常一致的分割结果.因此，算法可以被用于分析不同部位的运动.

3.2比较分析

为了进一步说明算法的有效性，和已有典型分割算法进行比较分析.在已有分割算法中，SDF是一种非常有效的层次分割方法.能够得到较为一致的分割结果.但SDF算法由于受姿态变化等影响，分割结果仍旧具有明显的不一致性.而且只根据形状特征进行分割聚类，也会导致分割结果无法满足用户要求.而笔者提出的算法引入了三维数据对齐和用户少量交互完成用户交互标记的传递，从而能够快速地完成三维动画模型一致性分割.图6左右分别给出了SDF分割结果和笔者算法得到的结果.可以发现：SDF分割结果难以有效地反映出人体层次结构，而且不一致.和SDF算法比较，笔者算法由于考虑了用户交互，从而使分割结果很好地逼近用户意图，保证不同帧分割结果的一致性.而对用户来说，额外的操作只需要在一个帧上定义标记，用户应该可以接受.

图6　一致性结果比较分析Fig.6　Comparison of consistent segmentation results

4结论

针对三维动画序列提出通过用少量户交互来解决分割一致性问题，通过三维数据对齐完成用户标记点的映射.用户只需对第一帧进行交互就可以完成对整个序列的分割，因此用户可以接受这种交互.通过实验分析表明：算法能够适用于不同类型的动画网格序列，而且明显要优于已有分割方法.在后续研究中，有很多可以改进的地方.比如，Kaplansky等提出了更为有效的边界优化算法[18]，可用于边界优化.此外，笔者采用MDS这样的全局对齐得到外点，无法适用于具有遮挡关系的局部数据，模型匹配技术得到了广泛的研究[19]，因此可以通过局部点的特征匹配来进一步提高分割准确率.

参考文献：

[1]KALOGERAKIS E, HERTZMANN A, SINGH K. Learning 3D mesh segmentation and labeling[J]. ACM Transactions on Graphics,2010,29(4)：102.

[2]郑河荣,刘家好,何玲娜.脑血管计算机模型的建立与有限元分析[J].浙江工业大学学报,2014,42(3)：253-256.

[3]KRAEVOY V, SHEFFER A. Cross-parameterization and compatible remeshing of 3D models[J]. ACM Transactions on Graphics,2004,23(3)：861-869.

[4]潘翔,陈敖,周春燕,等.基于视图特征点分布的三维模型检索算法[J].浙江工业大学学报,2013,41(6)：641-645.

[5]MANGAN A P, WHITAKER R T. Partitioning 3D surface meshes using watershed segmentation[J]. Visualization and Computer Graphics, IEEE Transactions on,1999,5(4)：308-321.

[6]TAL A, KATZ S. Hierarchical mesh decomposition using fuzzy clustering and cuts[J]. ACM Transactions on Graphics,2003,22(3)：954-961.

[7]SHAPIRA L, SHALOM S, SHAMIR A, et al. Contextual part analogies in 3D objects[J]. International Journal of Computer Vision,2010,89(3)：309-326.

[8]FANG Yi, SUN Mengtian, KIM M, et al. Heat-mapping：a robust approach toward perceptually consistent mesh segmentation[C]//2013 IEEE Conference on Computer Vision and Pattern Recognition. Colorado Springs：IEEE Computer Society,2011：2145-2152.

[9]SIDI O, KAICK O, KLEIMAN Y, et al. Unsupervised co-segmentation of a set of shapes via descriptor-space spectral clustering[J]. ACM Transactions on Graphics,2011,30(6)：126.

[10]HU Ruizhen, FAN Lubin, LIU Ligang. Co-segmentation of 3D shapes via subspace clustering[J]. Computer Graphics Forum,2012,31(5):1703-1713.

[11]ZHENG Youyi, TAI C L, AU O K C. Dot scissor：a single-click interface for mesh segmentation[J]. IEEE Transactions on Visualization and Computer Graphics,2012,18(8)：1304-1312.

[12]MENG Min, FAN Lubin, LIU Ligang. A comparative evaluation of foreground/background sketch-based mesh segmentation algorithms[J]. Computers & Graphics,2011,35(3)：650-660.

[13]ZHENG Youyi, TAI C L. Mesh decomposition with cross-boundary brushes[J]. Computer Graphics Forum,2010,29(2)：527-535.

[14]FAN Lubin, LIC L, LIU Kun. Paint mesh cutting[J]. Computer Graphics Forum,2011,30(2)：603-612.

[15]SILVA V D, TENENBAUM J B. Sparse multidimensional scaling using landmark points[R]. California：Stanford University,2004.

[16]AGATHOS A, PRATIKAKIS I, Perantonis S, et al. Protrusion-oriented 3D mesh segmentation[J]. The Visual Computer,2010,26(1):63-81.

[17]VLASIC D, BARAN I, MATUSIK W, et al. Articulated mesh animation from multi-view silhouettes[J]. ACM Transactions on Graphics,2008,27(3)：97.

[18]KAPLANSKY L, TAL A. Mesh segmentation refinement[J]. Computer Graphics Forum,2009,28(7)：1995-2003.

[19]潘翔,章国栋,周春燕,等.三维可变形物体的三点匹配策略[J].浙江工业大学学报,2013,41(5)：539-544.

(责任编辑：陈石平)

User-constrained consistent segmentation of 3D animated meshes

PAN Xiang1, TONG Weihuai1, XU Hongtao2, WAN Zhixing1

(1.College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China;

2.Data Management Centre, Human Resouces and Social Security of Zhengzhou, Zhengzhou 450006, China)

Abstract:Existing approaches will cause inconsistent segmentations for 3D animated meshes. To address this issue, we propose an algorithm of interactive segmenting 3D animated meshes based on 3D data correspondence and it can obtain highly consistent segmentations with user’s interactions. In this algorithm, the first frame should be annotated interactively. Then the principal component analysis is used to align different frames of animation. Then user’s mark can be automatically mapped to other models. Finally, based on directional angle, the cut algorithm is designed and the boundary is optimized according to the curvature of the joint mode until the segmenting results are satisfied. Experimental results show that the algorithm can effectively segment artificial 3D animation and multi-view reconstruction animation. Furthermore, the proposed algorithm can effectively improve the segmenting quality better than the existing algorithms.

Keywords:3D animated meshes; interactive segmentation; graph cut; 3D mesh correspondence

文章编号：1006-4303(2015)04-0420-05

中图分类号：TP391

文献标志码：A

作者简介：潘翔(1977—)，浙江文成人，教授，博士，研究方向为计算机图形学，E-mail：panx@zjut.edu.cn.

基金项目：国家自然科学基金资助项目(6127230)；浙江省文物局基金资助项目(2014014)

收稿日期：2014-12-08