钢筋混凝土三点弯曲梁裂缝扩展过程模拟

钢筋混凝土三点弯曲梁裂缝扩展过程模拟

胡少伟，米正祥

(南京水利科学研究院，江苏南京210029)

摘要：改进后的扩展有限元法位移函数能够更好地反映真实的裂缝尖端渐近位移场，而且无需后处理便可求得应力强度因子，从而为分析裂缝扩展过程提供了便利。为研究钢筋混凝土三点弯曲梁裂缝扩展过程的规律，采用改进后的扩展有限元方法模拟了不同配筋率和不同钢筋位置的三点弯曲梁。文中阐述了改进后扩展有限元法的基本原理，利用虚功原理推导了其支配方程，并介绍了钢筋混凝土三点弯曲梁的应力强度因子计算方法。研究表明：对于超筋结构，起裂断裂韧度与试件配筋率无关；钢筋处于临界位置时起裂韧度与失稳韧度均达到最小值0.567和1.666 9 MPa·m`(0.5)，且钢筋贯穿裂缝时的断裂韧度小于钢筋未贯穿裂缝时的值，对含有宏观裂缝的结构进行锚杆加固时应将锚杆置于裂缝前端。

关键词：钢筋混凝土； 三点弯曲梁； 改进后扩展有限元； 配筋率； 断裂韧度

中图分类号：TU375.1

文献标志码：A

文章编号：1009-640X(2015)03-0009-09

Abstract：The displacement mode of the improved extended finite element method can reflect the true crack tip displacement and the stress intensity factor can be obtained without post-processing, so it is convenient to analyse the crack propagation process. In order to study the laws of crack propagation process, the reinforced concrete three-point bending beams having different steel reinforcement ratios and different positions are simulated by using the improved extended finite element method.The basic theory of the improved extended finite element method is studied, the governing equation is derived by using the virtual work principle, and then the stress intensity factor calculation method is described. The crack propagation process of the reinforced concrete three-point bending beams with different parameters is simulated by using the improved extended finite element method. The research results show that the initial fracture toughness is independent of reinforced ratio for surplus reinforcement beam. The fracture toughness reaches the minimum values when the bars are in the critical positions, which are larger when the bars don’t run throughout the cracks than the bars running throughout the cracks. The bolt should be placed in the front of crack tip when the structure containing macroscopic crack is reinforced.

DOI:10.16198/j.cnki.1009-640X.2015.03.003

收稿日期：2014-09-05

基金项目：国家自然科学基金资助项目(51278230，51378241)；高等学校博士学科点专项科研基金资助项目

作者简介：刘荣桂(1957—)， 男， 江苏江都人，教授，主要从事混凝土结构耐久性研究。E-mail：liurg@ujs.edu.cn

钢筋混凝土结构受力破坏过程也就是裂缝的扩展过程，深入研究其裂缝扩展机理以及影响其断裂参数的不同因素，对钢筋混凝土结构裂缝稳定性检测、裂缝安全评价以及对已建工程进行合理的加固具有重要的工程价值和实践意义[1]。扩展有限元法是目前求解裂缝扩展等不连续问题最有效的数值计算方法，它最早由美国西北大学T. Belytschko教授为代表的研究组提出[2]，2000年，被该课题组正式命名为扩展有限元法(XFEM: Extended Finite Element Method)。

扩展有限元法以单位分解法为基础，在常规的有限元位移模式中增加反映局部特性的附加函数，以反映结构的不连续性；如在模拟裂纹扩展时，被裂纹分开的单元节点用广义的Heaviside函数加强，以反映裂纹面的不连续性，对包含有裂缝尖端的单元节点用裂缝尖端渐近位移场函数进行加强，以反映裂缝尖端区域的局部特性[3-4]。由于该方法在分析裂缝扩展等不连续问题时具有独特的优势，提出后在短短的几年里便得到了快速发展与广泛应用，也为断裂力学数值模拟开辟了一条新途径[5]。

B. L.Karihaloo等[6]陈述了XFEM在静态裂纹问题中的应用，并与广义有限元法进行了比较。N. Sukumar等[7]陈述了如何在传统有限元程序上实现XFEM功能，并利用改进后的程序模拟了复合材料的裂缝扩展问题。为了分析形状复杂的多裂纹断裂问题，M. Stolarska等[8]把水平集法与XFEM结合起来研究动态裂纹的扩展问题，这样通过水平集法可以方便的追踪裂纹与裂缝尖端位置，确定裂纹的扩展速率与扩展方向，通过XFEM计算应力和应变。N. Sukumar等[9]利用裂缝尖端位移逼近函数改进了裂缝尖端节点，通过区域积分法计算了复合型裂缝的应力强度因子，并提出用新的约束三角化算法形成初始有限元网格的方法。X. Y. Liu等[10-11]为了改善计算精度，对含有裂缝尖端单元的结点位移场函数进行了调整，他不但使用裂缝尖端位移场的主要项，还使用了高阶项；同时，他还证明了改进后的位移近似函数与实际的裂缝尖端渐近位移场是等价的。余天堂[12]利用虚功原理导出了扩展有限元法求解的支配方程，给出了求解不连续函数的积分方法，探讨了缝尖应力强度因子的计算方法。方修君等[13]利用虚设节点法，在通用有限元程序内嵌入了扩展有限元法的功能，改进了三角形子域积分算法，推导了子域积分与Heaviside函数间的关系。董玉文等[14]推导了重力坝水力劈裂问题的有限元列阵，给出了水压力作用下XFEM的实现方法，并通过模拟向家坝重力坝坝踵水力劈裂问题，展示了这种方法的优越性。

本文利用改进后的扩展有限元法对钢筋混凝土三点弯曲梁裂缝过程进行数值模拟，并讨论配筋率、钢筋位置等不同因素对混凝土断裂参数的影响。

1改进后扩展有限元法

1.1位移模式的建立

图1　含任意裂纹单元节点加强示意 Fig.1 Node strengthening of arbitrary crack unit

Bellyschko等构造位移模式时，裂纹尖端单元节点加强函数只选取了裂纹尖端渐近位移场函数的主要项，而且假定裂纹尖端周围被加强节点的附加系数是相互独立的，这样加强的位移场并不是真实的裂纹尖端渐近位移场。为了改善计算精度，对含有裂缝尖端的单元节点进行加强时，在使用裂纹尖端渐近位移场函数主要项的同时还应采用高阶项；不但对裂缝尖端单元节点(第1层需要改进的单元)进行加强，而且对裂缝尖端单元周围的外层单元(分别为第2层、第3层等需要改进的单元)也应进行加强。

如图1所示的含有一条任意裂缝的平面断裂问题，改进后的扩展有限元离散位移表达式[10]为：

(1)

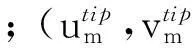
需要说明的是，一个节点不能同时属于裂纹尖端单元和被裂纹贯穿的单元，如二者冲突，则该节点应优先属于裂纹尖端单元。

裂纹尖端渐近位移场函数的一般表达式[15]为：

(2)

(3)

式中：ν为泊松比；μ为剪切模量；对于平面应变问题,κ=3-4ν，对于平面应力问题,κ=(3-ν)/(1+ν)。

将式(2)代入式(1)可得：

(4)

式中：Mk为裂缝尖端所在单元的节点集合，第1层需要改进的单元为Mk1，第2层需要改进的单元为Mk2，则裂纹尖端改进单元Mk=Mk1∪Mk2。

1.2支配方程的建立

改进后扩展有限元法的位移模式构造好后，其支配方程便可用虚功原理推导[12]。如果结构发生了一个虚位移δu，空间任意含裂纹的弹性体等效积分形式为：

(5)

式中：f为单位体积力；Ω为不包含裂纹面的三维体。

由应力张量的对成性与Green公式可得：

(6)

(7)

将改进后扩展有限元法的位移表达式代入式(7)，便可得改进扩展有限元的支配方程为：

Kd=R

(8)

式中：d为节点未知自由度向量，对于加强节点，不仅包括常规自由度u，还包含了附加自由度a与b;K为整体刚度矩阵，由单元刚度矩阵组装得到，其表达式为：

(9)

(10)

(11)

R为整体荷载列阵，由单元荷载列阵组装得到，其表达式：

(12)

(13)

(14)

(15)

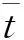
1.3应力强度因子的计算

应力强度因子是表征裂纹尖端应力应变场强度的重要参量，其不仅与裂纹的几何形状有关，而且与荷载形式也有关系。应用扩展有限元法进行断裂分析时，应力强度因子的计算方法有直接法与间接法。间接法是指先计算能量释放率，然后利用它与应力强度因子之间的关系换算得到应力强度因子，常用的方法有能量法、柔度法、J积分法等。直接法是指先计算裂纹尖端附近的应力与位移，然后将计算结果代入相应的应力强度因子计算公式，直接得到应力强度因子。

2裂缝模拟计算实例

2.1不同配筋率三点弯曲梁裂缝扩展过程

强度等级C60的钢筋混凝土三点弯曲梁计算模型见图3，试件长、高、宽分别为1 000, 200和120 mm，跨度800 mm，初始裂缝长80 mm。混凝土受拉应力区配置两根光圆热轧钢筋HPB235，钢筋直径为3，4，5，6，8和10 mm时，配筋率ρs分别为0.59%，1.05%，1.63%，2.38%，4.21%和6.54%，钢筋保护层厚度为25 mm。混凝土梁采用8节点实体单元(C3D8R)，网格密度为50×13×6；钢筋采用桁架单元(T3D2)，网格密度为100×2。左端采用铰支座，右端采用滑动支座，采用位移加载方式，最大主拉应力牵引损伤开裂准则。通过定义“Embeded Region”这一相互作用关系，将钢筋嵌入混凝土中来实现钢筋与混凝土之间的协同工作，不考虑钢筋与混凝土之间的滑移。加载点和支座处各加一刚性垫块，垫块与混凝土梁之间采用绑接约束，并通过设置垫块的弹性模量将其变形控制在很小范围内。

混凝土弹性模量E=36 GPa，泊松比ν=0.167，质量密度ρ=2 400 kg/m3，极限抗拉强度ft=2.20 MPa，断裂能Gf=147 N/m。钢筋的弹性模量Es=2.06×105MPa，泊松比ν=0.3，质量密度ρ=7 800 kg/m3，屈服强度fy=235 MPa。

裂纹扩展路径图、σx应力云图以及y方向位移云图见图2。由图可知，应力与位移均呈对称分布，加载点处存在显著地压应力区，混凝土拉应力最大值发生在裂纹尖端附近，并且在此处应力集中现象非常明显，能够较好地模拟裂纹尖端应力场的奇异性。挠度最大值出现在跨中位置，裂纹沿预制裂缝延长线方向竖直向上扩展，与典型的Ⅰ型裂纹扩展相吻合，并且裂纹的扩展过程不依赖于网格边界，裂纹在单元内部扩展，在模拟裂纹扩展过程时并不需要重新划分网格。

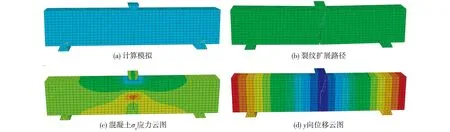
图2　计算模型及结果 Fig.2 A calculation model and results

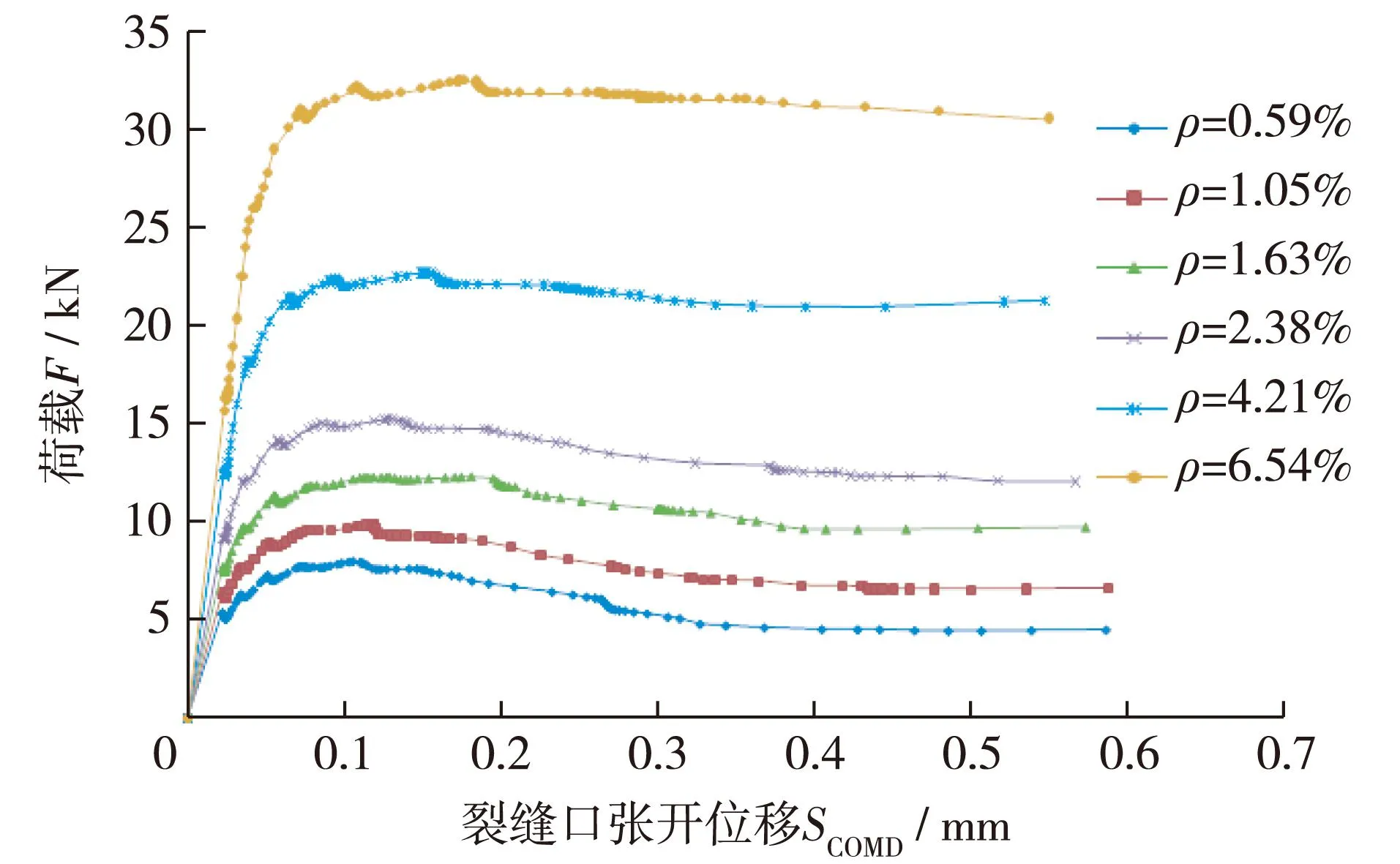
图3　不同配筋率试件的F-S COMD曲线 Fig.3 F-S COMDcurves for specimens of different reinforcement ratios

图3为不同配筋率试件的荷载-裂缝口张开位移(F-SCOMD)曲线。由图可知，在加载的初始阶段荷载F与裂缝口张开位移SCOMD之间呈线性关系，当加载至某一步使混凝土开裂后，F与SCOMD之间不再呈线性关系，混凝土表现出黏弹性特性；随着加载步的继续，荷载逐渐增大到峰值荷载，之后便开始卸载，但是卸载过程非常缓慢，主要是因为加载过程进行到后期，混凝土逐渐退出工作，由钢筋单独承受外荷载，并且当荷载下降到一定值后，钢筋混凝土试件的F-SCOMD曲线表现出与钢筋的荷载-应变(F-ε)曲线相似的特性。

配筋率ρs越大，F-SCOMD曲线越陡，上升段斜率越大，在相同的荷载增量下，裂缝口张开位移增量越小，发生单位位移所需要的能量亦越大，结构的延性越差。随着配筋率ρs的增加，F-SCOMD曲线的临界点逐渐后移，临界裂缝口张开位移SCOMDc逐渐增大。钢筋混凝土试件的起裂荷载与失稳荷载亦随ρs的增大而逐渐增大。不同配筋率试件的断裂参数和断裂韧度见表1和2。

表1　不同配筋率试件的断裂参数

由表1可知，混凝土开裂和失稳时刻的外荷载和钢筋约束力均随配筋率ρs的增大而逐渐增大，而且增大速度也越来越快。临界有效裂缝长度ac随配筋率ρs的增大而逐渐减小，并且减小幅度逐渐增大。说明配筋率ρs越大，钢筋对混凝土的约束作用越强，裂缝的扩展越不充分，结构的延性越差，并且当配筋率ρs增大到一定值后，结构将由延性破坏转变为脆性破坏。

表2　不同配筋率试件的断裂韧度

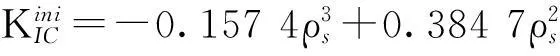
(16)

(17)

其中，式(16)和(17)的回归系数分别为0.999 8和0.975 2。

2.2不同钢筋位置三点弯曲梁裂缝扩展过程

钢筋截面中心到试件底部的距离分别为45，50，55，60，65和70 mm，初始裂缝长度为60 mm，试件长、高、宽分别为1 000，200和120 mm，跨度为800 mm。在每个试件混凝土受拉应力区配置两根光圆热轧钢筋HPB235，钢筋直径为8 mm。混凝土梁采用8节点实体单元(C3D8R)，网格密度为50×13×6；钢筋采用桁架单元(T3D2)，网格密度为100×2。

混凝土弹性模量E=36 GPa，泊松比ν=0.167，密度ρ=2 400kg/m3，极限抗拉强度ft=2.20 Mpa，断裂能Gf=147 N/m；钢筋弹性模量Es=2.06×105MPa，泊松比ν=0.3，密度ρ=7 800 kg/m3，屈服强度fy=235 MPa。

图4为钢筋到试件底部距离为70 mm的试件加载至不同步时的应力云图。由图4可知，整个加载过程中应力基本呈对称分布，加载点附近存在压应力区，预制缝两侧的混凝土可以继续承受荷载，并且应力分布呈拱形。拉应力最大值出现在裂缝尖端位置，应力集中现象比较明显，能够很好地模拟裂缝尖端的应力奇异性。裂缝沿预制裂缝竖直向上扩展，破坏形式符合Ⅰ型断裂。

当加载至第14步时，裂缝尖端位置的混凝土由于应力集中而开裂，并且裂缝开始向前扩展，随着裂缝的扩展，中性轴逐渐上移，受拉应力区逐渐增大，受压应力区逐渐减小，当加载至第69步时，受压应力区已消失，这种受力特性持续到第98步，之后又出现受压应力区，直至整个结构发生失稳破坏(第190步)。

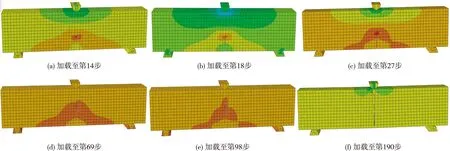
图4　裂纹扩展过程 Fig.4 Crack propagation process

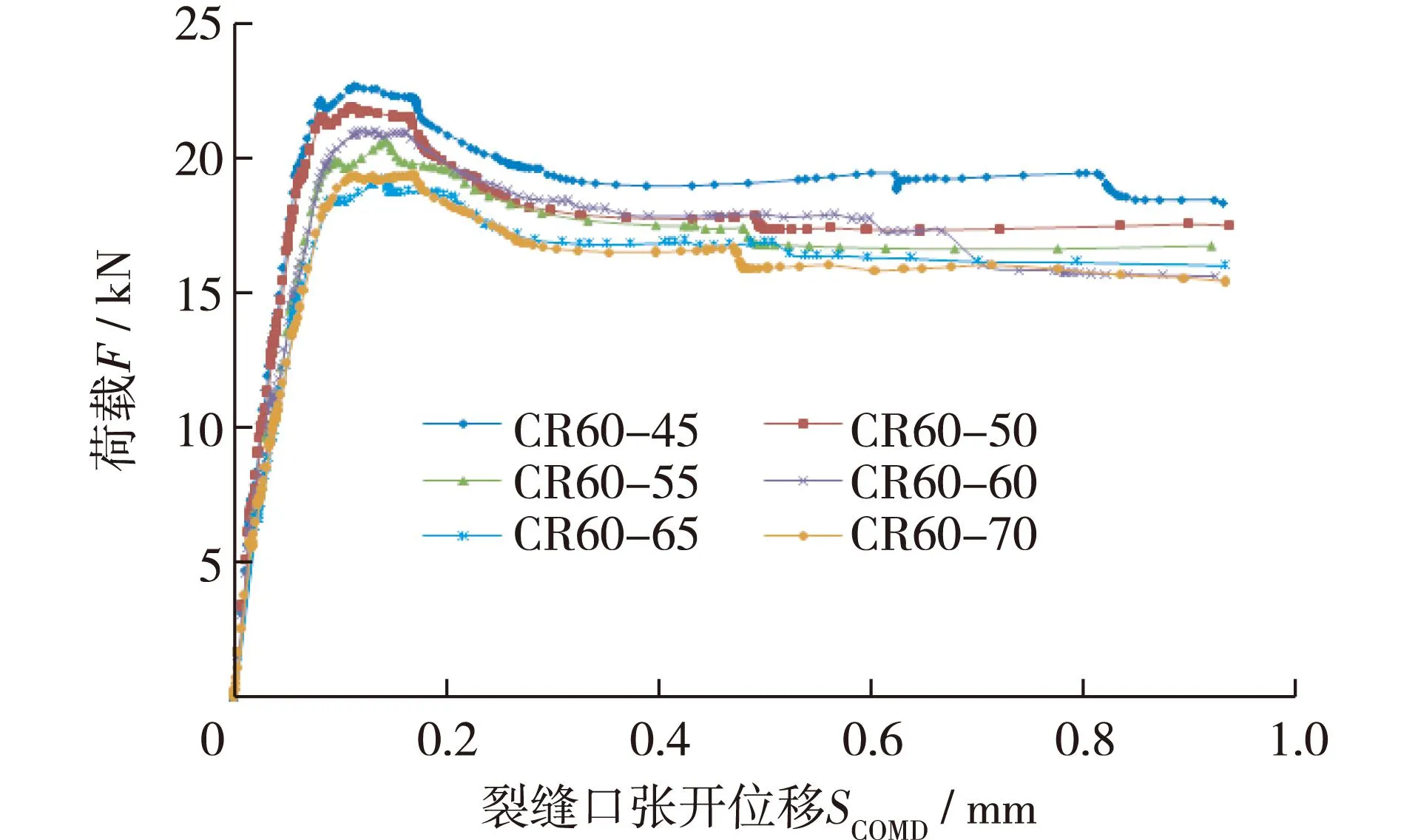
图5　不同钢筋位置试件的F-S COMD曲线 Fig.5 F-S COMDcurves for specimens having different reinforced positions

图5为不同钢筋位置的各试件荷载-裂缝口张开位移(F-SCOMD)曲线。由图5可知，开裂之前，钢筋混凝土试件的F-SCOMD曲线基本与钢筋位置无关，即F-SCOMD曲线的线性段接近重合，并且各试件的卸载段部分基本平行，说明钢筋位置对结构的刚度影响很小。起裂荷载与失稳荷载随着钢筋距试件底部距离的增大而逐渐减小，但减小程度不明显，说明钢筋位置对混凝土试件的起裂荷载与失稳荷载有一定影响，但影响不大。

表3给出了各试件的起裂荷载、失稳荷载、钢筋约束力以及临界有效裂缝长度等断裂参数。由表可知，起裂荷载Fini随钢筋到试件底部距离的增大而逐渐减小，当钢筋刚好在裂缝尖端时，起裂时刻的外荷载与钢筋约束力均达到最小值。失稳荷载Fmax亦具有与起裂荷载相似的规律。

由于钢筋到试件底部的距离越远，钢筋对裂缝的约束作用越弱，断裂过程区在荷载作用下的扩展越充分，结构的延性越好，临界有效裂缝长度ac就越大；但是随着钢筋距试件底部距离的增大，其越来越接近试件上边界，断裂过程区受上边界的约束作用越来越强，裂缝扩展也就越不充分了，因而临界有效裂缝长度ac增大到一定值后反而开始减小。当钢筋刚好在初始裂缝尖端时，裂缝尖端的钢筋阻止了裂缝尖端继续扩展，断裂过程区的发展也受到抑制，表现为临界有效裂缝长度ac明显减小。

表3　不同钢筋位置试件断裂参数

表4　不同钢筋位置试件断裂韧度

3结语

本文详述了改进后扩展有限元法的位移模式，推导了采用改进后扩展有限元计算时的支配方程，并给出了应力强度因子的计算方法，模拟了不同参数的钢筋混凝土三点弯曲梁裂缝扩展过程。算例表明，改进后的扩展有限元法能够很好地模拟裂缝尖端的应力奇异性，裂尖附近不需要布置高密度网格，不需要预先设置裂缝扩展路径，而且在裂缝扩展过程中不需要调整网格；根据模拟结果，利用最小二乘法可得到起裂断裂韧度、失稳断裂韧度与配筋率之间的简单关系式；钢筋置于预制裂缝尖端时起裂断裂韧度与失稳断裂韧度均达到最小值，分别为0.567 和1.666 9 MPa·m0.5，且钢筋贯穿裂缝时的起裂断裂韧度与失稳断裂韧度均小于钢筋未贯穿裂缝时的值，这为实际工程中锚杆加固提供了有效的参考依据。

参考文献：

[1]胡少伟, 米正祥. 标准钢筋混凝土三点弯曲梁双K断裂特性试验研究[J]. 建筑结构学报, 2013, 34(3): 152- 157. (HU Shao-wei, MI Zheng-xiang. Experimental study on double-K fracture characteristics of standard reinforced concrete three-point beam[J]. Journal of Building Structures, 2013, 34(3): 152- 157. (in Chinese))

[2]BELYTSCHKO T, BLACK T. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Method in Engineering, 1999, 45(5): 601- 620．

[3]MELENK J M. The partition of unity finite element method: Basic theory and applications[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139: 289- 314.

[4]HUANG R, SUKUMAT N. Modeling quasi-static crack growth with the extended finite element method Part II: Numerical applications[J]. International Journal of Solids & Structures, 2003, 40(26): 7539- 7552．

[5]MARIANI S, PEREGO U. Extended finite element method for quasi-brittle fracture[J]. International Journal for Numerical Methods in Engineering, 2003, 58(1): 103- 126.

[6]KARIHALOO B L, XIAO Q Z. Modeling of stationary and growing cracks in FE framework without remeshing： a state of the art review[J]. Computer and Structure, 2003, 81: 119- 129.

[7]SUKUMAR N, PREVOST J H. Modeling quasi-static crack growth with the extended finite element method Part I: Computer implementation[J]. International Journal of Solids and Structures, 2003, 40: 7513- 7537.

[8]STOLARSKA M, CHOPP D L, MOES N, et al. Modeling crack growth by level sets in the extended finite element method[J]. International Journal for Numerical Methods in Engineering, 2001, 5l(8): 943- 960.

[9]SUKUMAR N, SROLOVITZ D J，BAKER T J. Brittle fracture in polycrystalline microstructures with the extended finite element method[J]. International Journal for Numerical Methods in Engineering, 2003, 56: 2015- 2037.

[10]LIU X Y, XIAO Q Z, KARIHALOO B L. XFEM for direct evaluation of mixed mode SIFs in homogeneous and bi-materials[J]. International Journal for Numerical Methods in Engineering, 2004, 59(8): 1103- 1118.

[11]XIAO Q Z，KARIHALOO B L. Improving the accuracy of XFEM crack tip field using higher order quadrature and statically admissible stress recovery[J]. International Journal for Numerical Methods in Engineering, 2006, 66(9): 1378- 1410.

[12]余天堂. 含裂纹体的数值模拟[J]. 岩石力学与工程学报, 2005(24): 4434- 4439. (YU Tian-tang. Numerical simulation of a body with cracks[J]. Chinese Journal of Rock Mechanics and Engineering, 2005(24): 4434- 4439. (in Chinese))

[13]方修君, 金峰. 基于ABAQUS平台的扩展有限元法[J]. 工程力学, 2007, 24(7): 6- 10.(FANG Xiu-jun， JIN Feng. Extended finite element method based on ABAQUS[J]. Engineering Mechanics, 2007, 24(7): 6- 10. (in Chinese))

[14]董玉文, 任青文. 重力坝水力劈裂分析的扩展有限元法[J]. 水利学报, 2011, 42(11): 1361- 1367. (DONG Yu-wen，REN Qing-wen. An extended finite element method for modeling hydraulic fracturing in gravity dam[J]. Journal of Hydraulic Engineering, 2011, 42(11): 1361- 1367. (in Chinese))

[15]FLEMING M, CHU Y A, MORAN B, et al. Enriched element-free Galerkin methods for crack tip fields[J]. International Journal for Numerical Methods in Engineering, 1997, 40(8): 1483- 1504.

An extended finite element method for modeling crack propagation of reinforced concrete three-point bending beams

HU Shao-wei, MI Zheng-xiang

(NanjingHydraulicResearchInstitute,Nanjing210029,China)

Key words： reinforced concrete; three-point bending beams; an improved extended finite element method; reinforcement ratio; fracture toughness

刘荣桂， 徐洁， 陈素碧, 等. 基于相似理论的海工预应力混凝土构件寿命预测[J]. 水利水运工程学报, 2015(3): 18-23. (LIU Rong-gui, XU Jie, CHEN Su-bi, et al. Prediction analysis of service life of marine prestressed concrete structure based on similarity theory[J]. Hydro-Science and Engineering, 2015(3): 18-23.)

(20123227110006)