黏弹性介质中瑞利波频散曲线和衰减系数曲线的反演①

黏弹性介质中瑞利波频散曲线和衰减系数曲线的反演①

常冬梅1， 刘雪峰2

(1.天津职业技术师范大学天津市高速切削与精密加工重点实验室，天津 300222；

2.中国民航大学航空工程学院，天津 300300)

摘要：瑞利波具有能量大、信噪比高等特点，可以用来反演介质内部的力学信息，近年来在浅层地球物理勘探、深层地震学研究以及超声波无损检测等多个领域都有较广泛的应用。目前大多数瑞利波的应用中都假设介质是弹性的，然而实际中岩石、土壤和金属等介质都在一定程度上体现出了黏弹性。当介质的黏弹性较强时仍然采用弹性假设研究其中瑞利波的反演将增大误差，因此有必要考虑黏弹性介质中的瑞利波反演，但是目前这方面的研究仍不够深入。本文研究黏弹性介质中瑞利波频散曲线和衰减系数曲线的反演问题，给出其在半空间中联合反演的方法，并对该方法的误差进行分析。

关键词：瑞利波； 黏弹性； 波频散曲线; 衰减系数; 反演

收稿日期：①2014-08-20

基金项目：国家自然科学

作者简介：常冬梅(1983-),女(汉族),讲师,主要从事工程力学方面研究。E-mail:dm_chang@hotmail.com。

中图分类号:P631.4文献标志码：A

DOI:10.3969/j.issn.1000-0844.2015.03.0739

Inversion of Rayleigh Wave Dispersion Curves and Attenuation

Coefficient Curves in Viscoelastic Medium

CHANG Dong-mei1, LIU Xue-feng2

(1.TianjinKeyLaboratoryofHighSpeedCuttingandPrecisionMachining,TianjinUniversityofTechnologyandEducation,

Tianjin300222,China; 2.SchoolofAeronauticalEngineering,CivilAviationUniversityofChina,Tianjin300300,China)

Abstract：Rayleigh waves always have a corresponding large amount of energy and a high signal-noise ratio that can be used for the inversion of mechanical information. In recent years, the Rayleigh wave method has been increasingly used in geophysical exploration, seismology, and ultrasonic non-destructive testing. To date, most Rayleigh wave applications are assumed to be in elastic media. However, media such as soil and rocks can show viscoelastic characteristics, and there will be an associated error if the medium is assumed to be elastic. Therefore, it is important to study the inversion of Rayleigh waves in viscoelastic media, and as yet there has been little research on this topic. In this study, we investigate the inversion problem of Rayleigh waves dispersion curves and attenuation coefficient curves, present a method to invert Rayleigh waves dispersion curves and attenuation coefficient curves, and analyze the error associated with this method.

Key words： Rayleigh wave; viscoelasticity; wave dispersion curve; attenuation coefficient; inversion

0引言

瑞利波法是一种新兴的地球物理勘探方法，由于该波能量大、信噪比高，越来越多地应用到浅层地球物理勘探[1]、深层地震学研究[2]以及超声波无损检测[3]等领域。目前在瑞利波的应用中大多假设介质是弹性的，然而实际中岩石、土壤和金属等介质都在一定程度上体现出黏弹性，使理论研究成果与实际现象有一定的出入，阻碍了瑞利波的应用。当介质的黏弹性较强，例如对填海造地产生的软土进行检测时，仍然采用弹性假设研究其中瑞利波的反演将增大误差，因此有必要考虑黏弹性介质中的瑞利波反演。

关于黏弹性介质中瑞利波的研究，大多停留在正演计算方面。Day等[4]于1984年将Pade近似方法成功应用于黏弹性半空间的波场计算中；Carcione等[5-8]引入了记忆变量并利用拟谱方法对黏弹性半空间中的波场计算进行了一系列研究，收到了较好的效果。由于黏弹性介质对波有耗散作用，其半空间中的瑞利波存在频散，这与弹性半空间的情况不同，且不同频率的瑞利波的衰减系数不同，即还可以采集到衰减曲线，因此黏弹性半空间中需同时反演瑞利波的频散曲线和衰减系数曲线。但前人尚未深入进行黏弹性半空间介质中瑞利波的反演研究，本文将针对黏弹性半空间模型，给出一种可行的研究瑞利波频散曲线和衰减系数曲线的联合反演方法，并对该方法的误差问题进行分析。

1黏弹性半空间中的计算

Q值是刻画黏弹性介质耗散性质的重要参数，在很多理论和应用的研究中往往首先给定模型的Q值。而对于一个给定Q值和弹性条件的体波速度(或松弛模量)模型，若要计算其对应的横、纵波相速度和衰减系数，往往首先需要得到其对应的松弛时间。

其中

得到复模量后，可以得到黏弹性半空间中横、纵波的复速度：

由于横、纵波速度均为复数，设

式中x和y并非横、纵波的相速度和衰减系数，这两个参数定义为

将式(4)代入式(5),可以得到横、纵波的相速度和衰减系数的计算式：

当给定`Q值和弹性条件下体波速度(或松弛模量)时，由此可得到黏弹性半空间模型中横、纵波的相速度和衰减系数。

已有研究证明，将横、纵波的复速度直接代入弹性半空间中瑞利波相速度的显式解中即可得到黏弹性半空间中瑞利波复速度[11]。与体波完全相同的是，将瑞利波复速度代入式(6)、(7)中即可得到黏弹性半空间中瑞利波的相速度和衰减系数。本文采用Vihn等[12]提出的弹性半空间中瑞利波相速度的显式解，得到黏弹性半空间中瑞利波的复速度。

2反演模拟

一般用横、纵波的Q值(QS，QP)来描述黏弹性介质对波的耗散作用，通过反演瑞利波的频散曲线和耗散系数曲线，不仅可以得到介质的横波速度，还可以得到介质的Q值。与体波速度类似，瑞利波频散曲线和耗散系数曲线对QS的敏感性一般大于QP，因此通常反演QS的精度较高。本文中均假设纵波速度是横波速度的2倍，QP也是QS的2倍。瑞利波的反演是典型的优化问题，优化方法的选择会影响到反演的结果。选用多起点全局优化方法进行反演,尽量避免陷入局部极小值。

首先进行反演模拟来检验反演方法的有效性。以VS=200 m/s，VP=400 m/s，QS=15，QP=30的黏弹性半空间模型1为例，计算其对应的瑞利波频散曲线和耗散系数曲线(图1)。可以看到，黏弹性空间瑞利波发生了明显的频散现象，与弹性半空间明显不同,而且相速度随着频率的升高而加快。利用所得的频散曲线和耗散系数曲线进行反演。设反演初值VS=100 m/s，VP=200 m/s，QS=10，QP=20，反演结果见图2,反演所得的横波速度为199.78 m/s，QS为15.07，频散曲线和衰减系数曲线拟合度分别为99.88%和99.69%。反演结果与真实值相差极少。相对来说，Q值的反演结果误差略大，这与瑞利波频散曲线和衰减系数曲线对Q值的敏感性比横波速度低有关。

图1　模型1对应的瑞利波频散曲线和耗散系数曲线 Fig.1　Corresponding Rayleigh wave dispersion curve 　　　 and dissipation coefficient curve of model 1

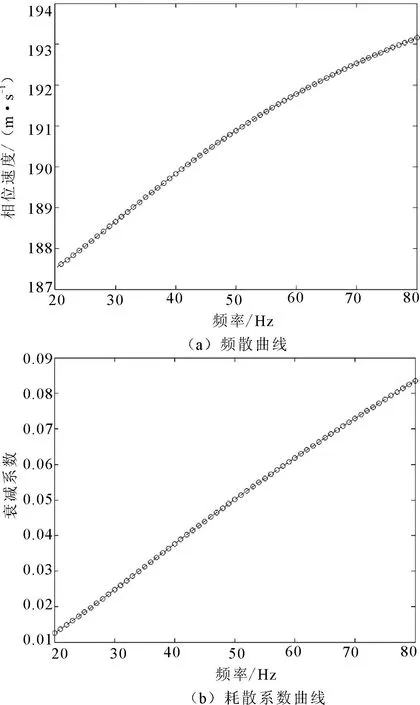
图2　对图1反演的结果 Fig.2　Inversion result of curves in figure 1

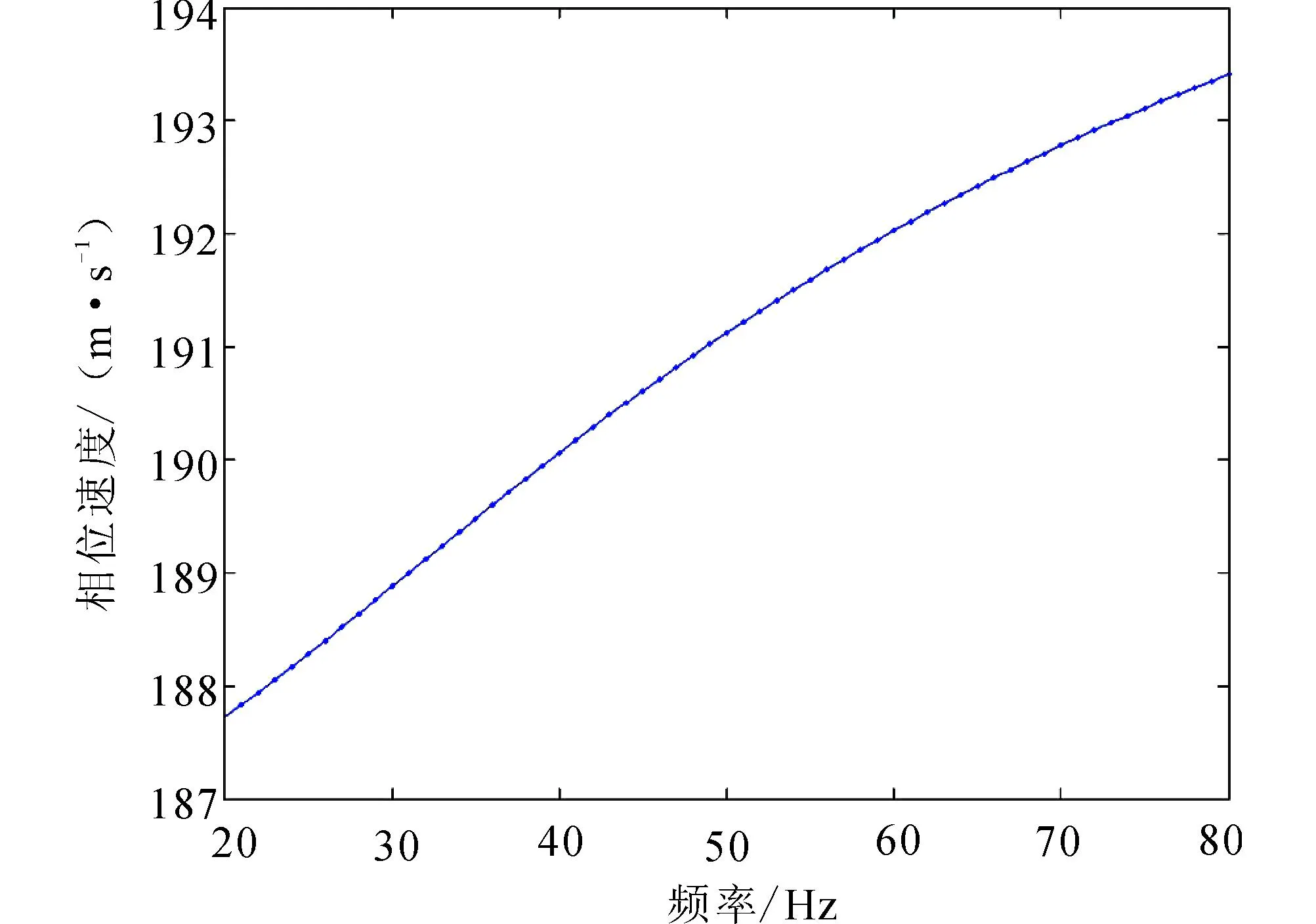
图3　基于弹性假设对图1反演的结果 Fig.3　Inversion result of curves in figure 1 based 　　　 on the elastic hypothetical theory

若基于弹性假设进行反演，得到的频散曲线反演结果见图3。反演所得的横波速度为201.5 m/s，相对于黏弹性假设下的结果来说，误差更大一些。在实际工程中，若Q值更小，即介质的黏弹性更强，基于弹性假设反演的误差将会更大。

3存在误差情况下的反演模拟

上述反演模拟是在没有噪声情况下进行的，在实际工程中由于各种干扰因素的存在，噪声是不可避免的。将图1中的瑞利波频散曲线加入5%的白噪声，用同样的反演初值和反演方法进行反演，结果见图4。反演所得的横波速度为202.99 m/s，QS为15.00。频散曲线和衰减系数曲线拟合度分别为98.65%和98.52%。相对于没有噪声的情况，反演误差有所增大，但是误差仍然较小，说明本方法在实际工程中也是可行的。尽管QS的反演结果非常接近真实值，但这只是一种巧合，需要和横波速度结果以及频散曲线和衰减系数曲线拟合度相结合，来综合判断反演结果。

图4　对图1中数据增加了白噪声后反演的结果 Fig.4　Inversion result of curves in figure 1 　　　 after adding white noise

若基于弹性假设进行反演，得到的横波速度为209.32 m/s。可以看出，加入了白噪声后，基于弹性假设得到的反演结果误差明显比基于黏弹性假设更大。这也说明在实际工程中，如果介质体现出较强的黏弹性性质，有必要基于黏弹性假设进行反演。

4结论

本文提出一种基于多起点优化方法的黏弹性半空间中瑞利波频散曲线和衰减系数曲线的反演方法。通过反演模拟发现该反演方法的精度较高，即使数据存在一定的噪声，反演结果仍然可以保持较高的精度。通过与弹性假设下反演结果对比可以看出，在实际工程中，当介质体现出较强的黏弹性性质时，基于黏弹性假设进行反演比基于弹性假设可以得到更高的精度，而且可以同时得到介质的Q值信息。

参考文献(References)

[1]Marone F,Van der Lee，Giardini S D.Three-dimensional Upper-mantle S-velocity Model for the Eurasia-Africa Plate Boundary Region[J].Geophysical Journal International,2004,158(1):109-130.

[2]Cascante G,Najjaran H，Crespi P.Novel Methodology for Nondestructive Evaluation of Brick Walls:Fuzzy Logic Analysis of MASW Tests[J].Journal of Infrastructure Systems,2008,14(2):117-128.

[3]Kuo B Y,Chi W C,Lin C R,et al.Two-station Measurement of Rayleigh-wave Phase Velocities for the Huatung Basin,the Westernmost Philippine Sea,with OBS Implications for Regional Tectonics[J].Geophysical Journal International,2009,179:1859-1869.

[4]Day S M,Minster J B.Numerical Simulation of Attenuated Wavefields Using a Padé Approximant Method[J].Geophysical Journal International,1984,78(1):105-118.

[5]Carcione J M,Kosloff D,Kosloff R.Wave Propagation Simulation in a Linear Viscoacoustic Medium[J].Geophysical Journal Royal Astronomical Society,1988, 93(2):393-407.

[6]Carcione J M,Kosloff D,Kosloff R.Viscoacoustic Wave Propagation Simulation in the Earth[J].Geophysics,1988,53(6),769-777.

[7]Carcione J M,Kosloff D,Kosloff R.Wave Propagation Simulation in a Linear Viscoelastic Medium[J].Geophysical Journal Royal Astronomical Society,1988c, 95(3):597-611.

[8]Carcione J M.Modeling Anelastic Singular Surface Waves in the Earth[J].Geophysics,1992,57(6):781-792.

[9]Blanch J O,Robertsson O A J,William W S.Modeling of a Constant-Q:Methodology and Algorithm for an Efficient and Optimally Inexpensive Viscoelastic Technique[J].Geophysics,1995,60：176-184.

[10] N H 瑞克，著.许云,译.黏弹性介质中的地震波[M].北京:地质出版社,1981.

Richer N H,Write.XU Yu ,Translate.Seisric Waves in Viscoelastic Medium[M].Beijing:Geological Publishing House,1981.(in Chinese)

[11]Maurizio R.Rayleigh Waves on a Viscoelastic Solid Half-space[J].Journal of the Acoustical Society of America,2001,110(1):59-67.

[12]Vinh P C,Ogden R W.on Formulas for the Rayleigh Wave Speed[J].Wave Motion,2004(39):191-197.