矩阵式编码智能算法在生产批量计划中的应用

（中国计量大学 质量与安全工程学院，杭州 310018）

生产批量计划问题是确定最优的生产批量计划，使得生产、生产准备和库存费用综合指标最小或利润最大[1-2]。受到资源约束的情况下，为消除各种资源间的冲突，需要同时对项目、时间和数量这三维变量进行调整[3-4]，随着求解问题规模的增大，精确解的计算量也增大。

遗传算法在求解大规模问题时易陷入局部最优解中，从而难以得到符合预期的解[5-7]。在研究生产批量计划问题时，也有学者将粒子群算法和遗传算法相结合，一定程度上弥补了GA局部搜索能力弱的缺陷，但可能以损失种群多样性为代价降低算法搜索效率，最终搜索得到的解不易满足预期要求。利用蚁群算法求解生产批量问题的相关研究较少，少数学者进行了一些研究，并将研究成果应用在固定的模型与生产实例中[8]。

本文对求解算法进行创新性的改进以提升算法性能。通过矩阵式编码的智能算法寻到近似最优的生产批量计划并将所求的结果与基本遗传算法和遗传粒子群算法进行对比，以证明改进算法提升了算法性能。

1 生产批量计划问题的数学模型

本文所考虑有能力约束的多级生产批量CMLLS（constrained multilevel lot-sizing）问题，问题描述为在给定的计划时间范围内，确定全部项目在不同时间段上的生产数量，使得总费用之和最小。CMLLS问题与实际生产计划更加贴近，是生产批量问题研究的重点。本文采用的数学模型为[9-10]

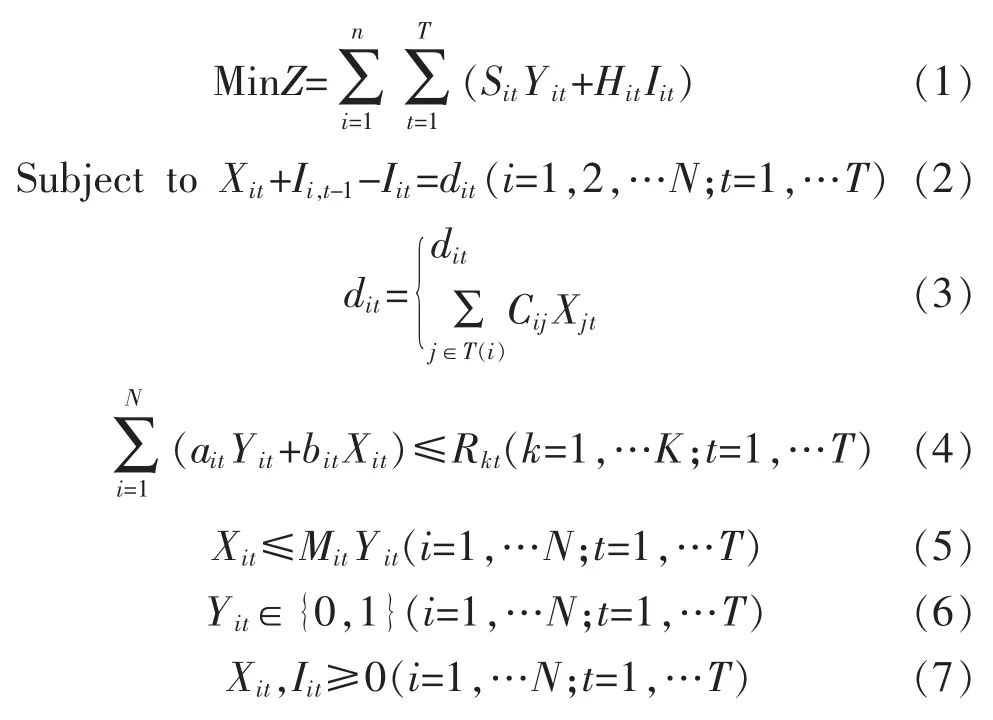
式（1）为总费用，包括生产准备费用及库存费用；式（2）为物流守衡方程；式（3）为需求公式，如果物料i是最终项目，则需求为外部需求，否则需求由当前物料i的所有后继物料的生产量决定；式（4）为资源约束条件；式（5）为只有在生产数量大于0时才能进行生产调整；式（6）为二进制决策变量，1表示生产，0表示不生产；式（7）为生产量和库存量不能为负数。

2 遗传算法的改进策略

2.1 改进方法

遗传算法求解过程本质上是随机寻优过程，但是遗传算法是按照概率随机进行的寻优操作，在大多数情况下只能得到全局范围的次优解，不易获得最优解，这是因为它的搜索是随机的，带有一定的盲目性[12]。

粒子群算法对自身参数的依赖很大，且初始粒子群是随机生成的，通常具有收敛速度慢、易陷入局部收敛等方面的缺陷[13]。

蚁群算法虽然通用性、鲁棒性较好，以及在各个领域的广泛应用近些年来受到越来越多的关注，但是把传统蚁群算法应用于求解涂料生产调度时，难以满足所有的约束条件[14]。

鉴于遗传算法、蚁群算法和粒子群算法存在一定的不足，本文将遗传算法、蚁群算法和粒子群算法融合以便于生产批量计划的求解，具体的计算步骤为

步骤1随机生成粒子位置，并按照上述算法得到初始种群（粒子群）。初始化全局极值和个体极值为第一个个体（粒子）的适应度函数值；

步骤2对当前种群（粒子群）的各个个体（粒子）描述求解适应度函数值；

步骤3按照适应度函数值对当前种群 （粒子群）进行排序，找出个体极值和全局极值；

步骤4选择：用5个随机的新个体替换种群（粒子群）中适应度函数值较差的5个个体（粒子）；

步骤5交叉：以轮盘赌博方式，改变种群（粒子群）中的部分个体（粒子）的特性；

步骤6变异：采用粒子群算法的更新规则对种群（粒子群）中的所有个体（粒子）进行更新；

步骤7变异：采用蚁群算法的信息素全局更新规则中的所有个体（粒子）进行更新；

步骤8变异：采用蚁群算法的信息素局部更新规则中的所有个体（粒子）进行更新；

步骤9查看是否达到最大迭代次数，如果是则转步骤8，否则转步骤2；

步骤10仿真结束。

具体的改进结合蚁群算法的遗传粒子群算法的计算流程如图1所示。

2.2 编码方式

为使用本文提出的粒子群、蚁群和遗传算法结合的智能算法，我们将生产批量进行编码作为个体（粒子），其目的是让计算机能够利用矩阵计算以大幅提高计算效率。个体（粒子）选择1～2048之间的随机整数。具体的某粒子矩阵式编码表如表1所示。

为了使用粒子群算法的位置和速度更新公式，需要对粒子速度进行编码。具体的某粒子速度矩阵式编码表如表2所示。其中，粒子速度选择-128～128之间的随机整数。

定义粒子在粒子群算法中的更新算法。更新的粒子位置矩阵由旧的粒子位置矩阵和粒子速度矩阵相加，当新的粒子编码矩阵中的元素越界时，越界元素由新的1～2048之间的随机整数进行替换。

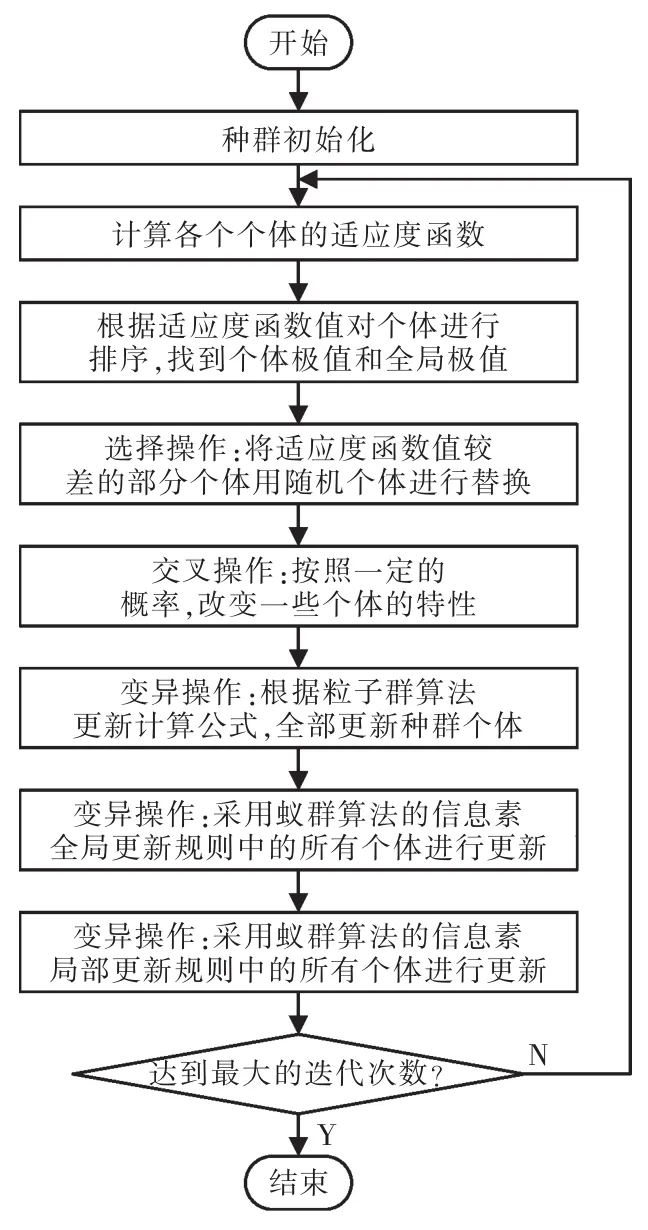
图1 改进的智能算法流程Fig.1 Flow chart of improved intelligent algorithm

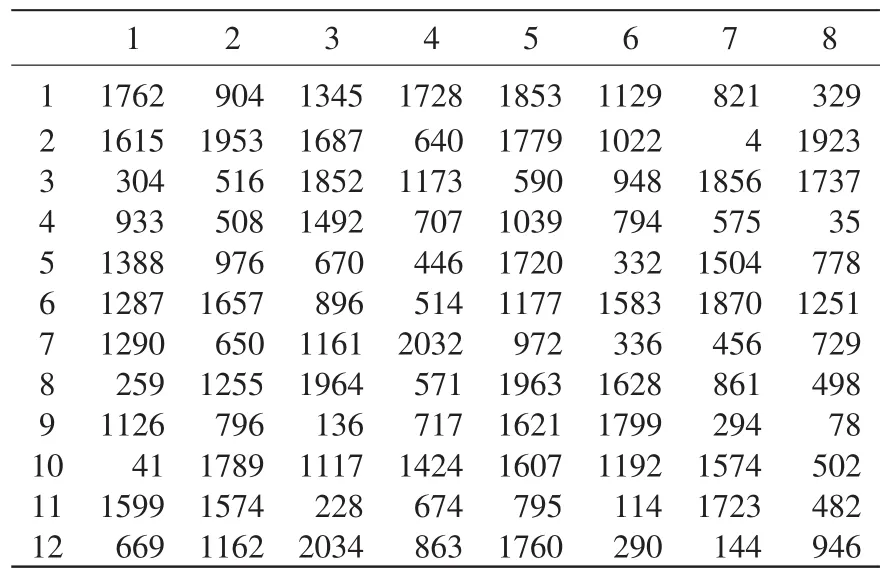
表1 某粒子矩阵式编码表Tab.1 A particle matrix encoding table

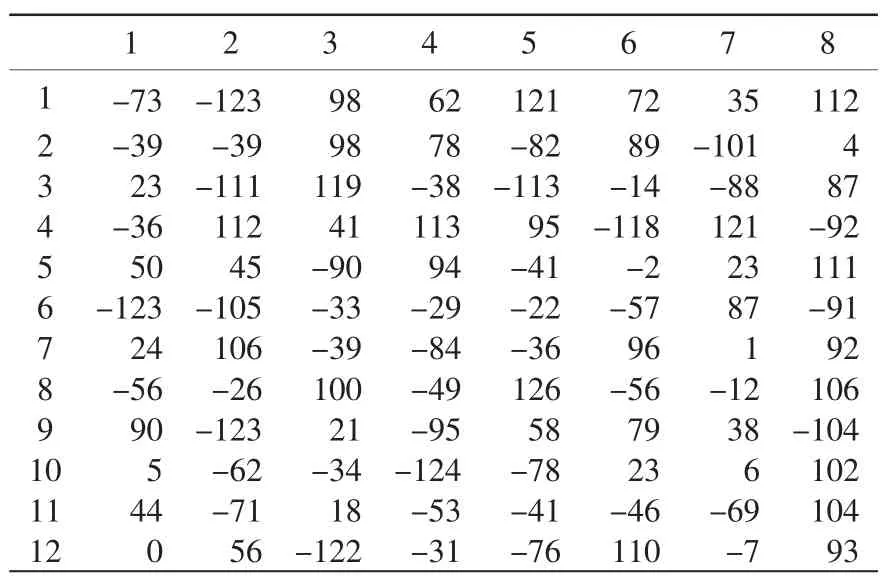
表2 某粒子速度矩阵式编码表Tab.2 A particle velocity matrix encoding table

本文在计算过程中采用矩阵计算。显然，相较于简单的数字计算，矩阵计算具有计算速度敏捷的优点。

3 实例测试

3.1 仿真实例

小型机是一种轻量型的计算机。本文收集到某计算机生产厂家接到一批2016年度的小型机订单，该订单要在一年内交付897台小型机，各月至少需要的交付数量为 51、8、45、98、86、57、6、181、139、57、27、142。生产1件小型机需要事先生产得到7个小型机箱体A和9件小型机外包装。由于电子器件寿命、员工工资变化、生产和装配造成的机器耗损和厂房维修等各种因素每月各异，小型机处理器、箱体和外包装的生产费用、装配费用、库存费用每月各异，具体如表3～表5所示。

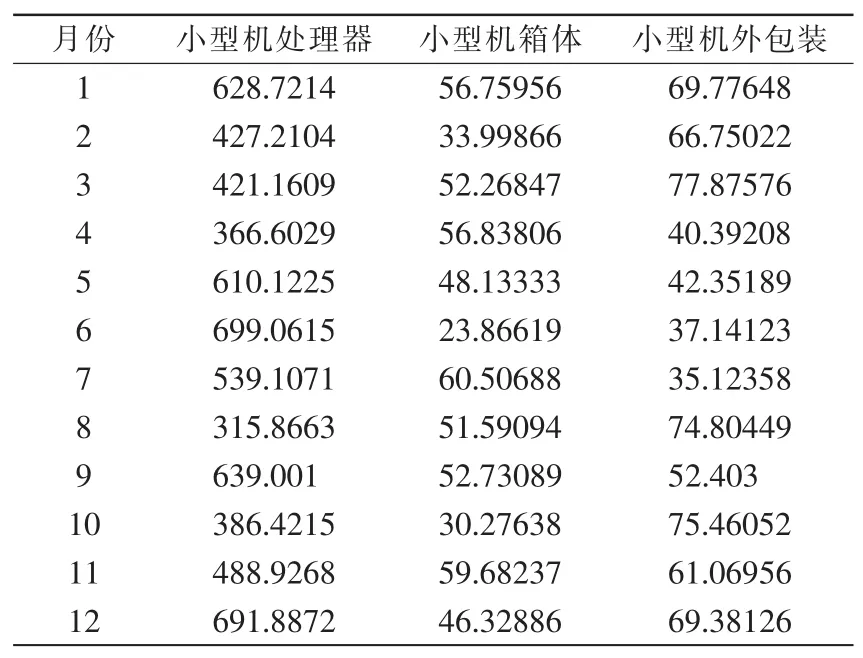
表3 小型机单件生产费用月度表（单位：元，每月平均值）Tab.3 Minicomputer piece production cost monthly report（Unit：Yuan，monthly average）

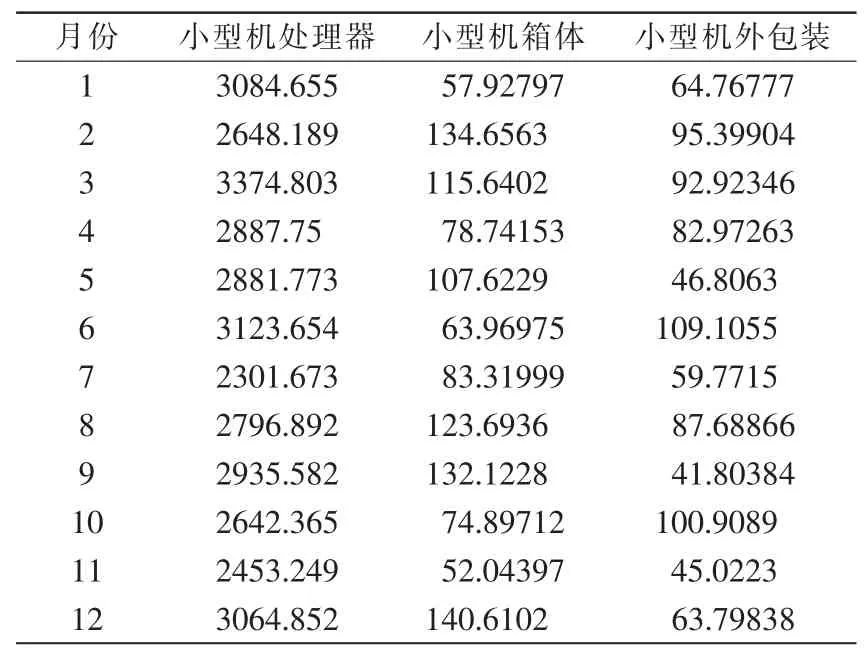
表4 小型机装配费用月度表（单位：元，每月平均值）Tab.4 Minicomputer assembly cost monthly report（Unit：Yuan，monthly average）

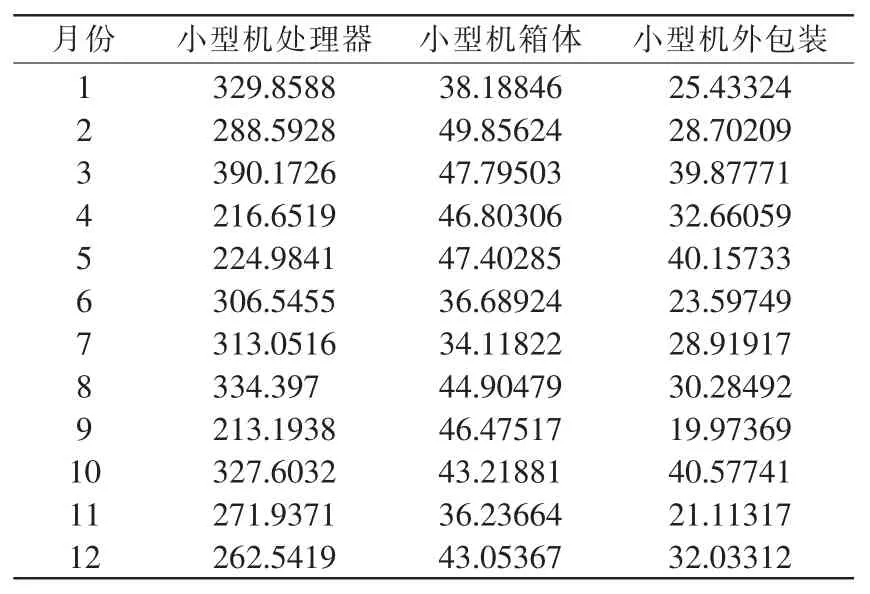
表5 小型机单件库存费用月度表（单位：元，每月平均值）Tab.5 Minicomputer piece inventory cost monthly report（Unit：Yuan，monthly average）

装配和生产小型机需要对小型机处理器、箱体和外包装的外侧喷塑（一层轻薄的塑料薄膜，生产和装配前贴住，生产和装配完成时揭下）以形成保护层，防止小型机处理器、箱体和外包装意外受损。由于温度、湿度等各种因素每月各异，每件部件的喷塑损失每月各异，具体如表6～表7所示。

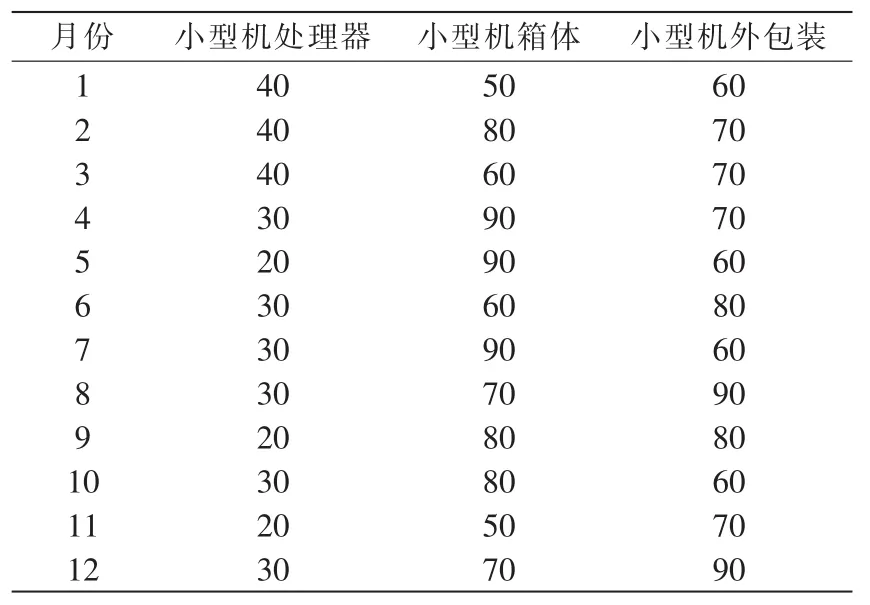
表6 小型机装配过程喷塑损失月度表（单位：cm3/件，每月平均值）Tab.6 Minicomputer spraying plastics losses monthly report in the assembling process（Unit：cm3/piece，monthly average）

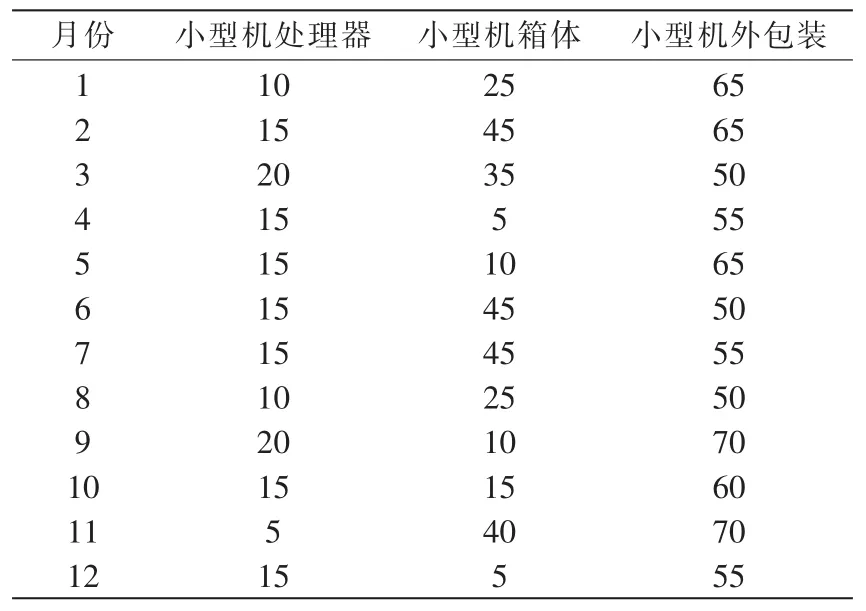
表7 小型机库存过程喷塑损失月度表（单位：cm3/件，每月平均值）Tab.7 Minicomputer spraying plastics losses monthly report in the inventory process（Unit：cm3/piece，monthly average）

厂家根据环境保障局的相关规定，计划生产该批次小型机造成的喷塑损失不超过645000 cm3。

厂家希望结合生产需求给出较为合理的生产批量计划以尽可能小的成本生产该批量897台小型机，即在上述条件下，寻求每个月的生产小型机的数量以使生产费用、装配费用和库存费用的综合成本费用尽可能的省。

3.2 仿真结果

对于上述实际应用算例，采用矩阵式编码的遗传算法、蚁群算法和粒子群算法结合的智能算法连续仿真20次可以得到下述仿真结果。具体的20次仿真过程中最优结果的当前代最优解与进化代数的关系曲线如图2所示。

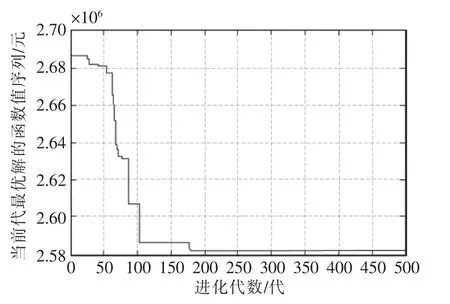
图2 当前代最优解与进化代数的关系Fig.2 Relation curve between the optimal solution of current generation and the evolutionary algebra

具体的20次仿真过程中最优解函数值和收敛代数与进化代数的关系曲线如图3所示。

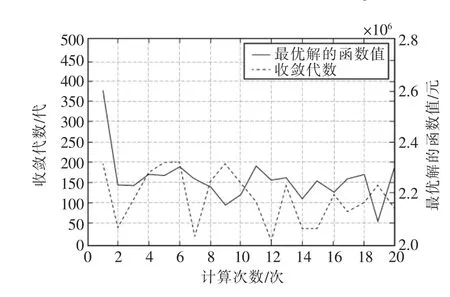
图3 最优解函数值和收敛代数与进化代数的关系Fig.3 Relation curve between the optimal solution and the convergence algebra of current generation and the evolutionary algebra

由图3可知，20次仿真过程中每一次计算得到的最优解函数值Y∈（2.2×106，2.3×106）元，收敛代数小于200代。证明了本文提出的智能算法具有良好的收敛性能，适于解决多级有资源约束生产批量计划问题。

本文基于上述实际应用算例对提出的矩阵式编码的智能算法和普通粒子群（PSO）算法和遗传算法进行对比测试。具体的测试结果如图4所示。

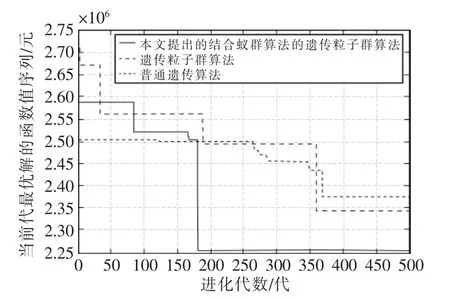
图4 实际应用算例的数学模型的测试结果Fig.4 Results of mathematical model of practical application example

由图4可知，本文提出的矩阵式编码的智能算法较优，得到的最优解更接近于实际最优解且收敛速度更快。最优解函数值Y＜2.25×106元。

为了验证本文提出的智能算法相比于基本粒子群算法收敛性更好，采用相同算例，多次试验仿真结果如表8所示。

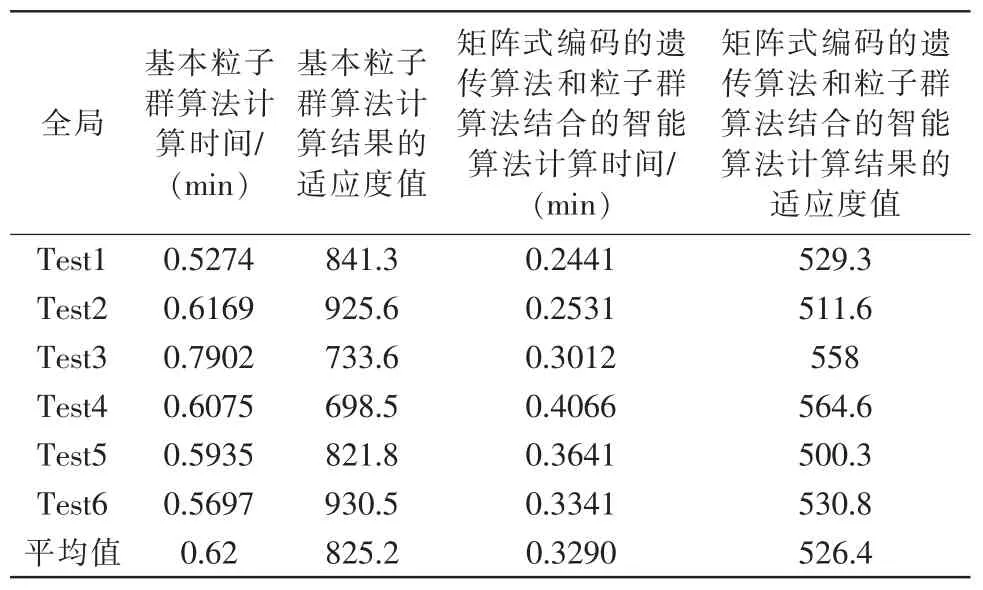
表8 改进的算法与粒子群算法的结果比较Tab.8 Comparison of the results of improved algorithm and particle swarm optimization algorithm

由表8可知，改进后的算法相比于基本粒子群算法，计算时间减少了一半左右，计算结果的适应度值也有明显改善。

4 结语

如何实现生产费用、生产准备费用和库存费用综合指标最小或利润最大，是关系企业生存与发展的重要课题。本文提出的一种新型的矩阵式编码的蚁群算法、遗传算法和粒子群算法相结合的智能算法有高速的计算性能、便于搜索近似最优解，可以得到比传统算法更好的计算效果，能满足当代企业对生产批量精确的要求。

[1]梁海峰.基于仿真的柔性自动化钢料加工车间规划设计研究[D].大连：大连理工大学，2005.

[2]屈国强.求解流水车间调度问题的瓶颈指向启发式算法[J].计算机集成制造系统，2012，18（2）：356-363.

[3]Ruiz R，V-R J A.The hybrid flowshop scheduling problem[J]. European Journal of Operational Research，2010，205（1）：1-18.

[4]周辉仁，唐万生，魏颖辉.柔性Flow-Shop调度的遗传算法优化[J].计算机工程与应用，2009，45（30）：224-226.

[5]唐海波，叶春明，刘长平，等.基于知识进化粒子群算法的模糊交货期流水车间调度问题[J].计算机集成制造系统，2012，18（4）：807-812.

[6]王圣尧，王凌，许烨，等.求解混合流水车间调度问题的分布估计算法[J].自动化学报，2012，38（3）：437-443.

[7]M N，Hansen P.Variable neighborhood search[J].Computers&Operations Research，1997，24（11）：145-184.

[8]李英俊，陈志祥.蚁群算法在单级多时段多资源约束的生产批量问题的应用研究[J].中国机械工程，2012，23（19）：2326-2330.

[9]Pan Q K，Ruiz R.An estimation of distribution algorithm for lot-streaming flow shop problems with setup times[J].Omega，2012，40（2）：166-180.

[10]周云鹏，题正义.遗传算法在组合优化中的应用[J].辽宁工程技术大学学报：自然科学版，2005，24（z1）：283-285.

[11]Xu Y，Wang L，Zhou G，et al.An effective shuffled frog leaping algorithm for solving hybrid flow-shop scheduling problem[C]// Proceedings of the International Conference on intelligent Computing，Zhengzhou，China：Springer，2011.

[12]唐立新，杨自厚，王梦光，等.CIMS中带多资源的CLMS问题的遗传启发式算法[J].系统工程理论与实践，1997，17（4）：39-44.

[13]马慧民，柳毅，叶春明.基于粒子群算法求解单级多资源约束生产批量计划问题[J].工业工程与管理，2005，10（6）：66-70.

[14]马艳，黄玲，苏受宝.含再制造的受限批量问题求解的蚁群算法[J].计算机应用与软件，2011，28（2）：96-99.