基于序列高斯协同模拟的多尺度区域森林碳密度空间分布估计

基于序列高斯协同模拟的多尺度区域森林碳密度空间分布估计

沈高云1张茂震1，2

(1.浙江农林大学环境与资源学院，浙江 临安 311300；

2.浙江农林大学浙江省森林生态系统碳循环与固碳减排重点实验室，浙江 临安 311300；)

摘要：以浙江省仙居县为例，基于2008年全县森林资源清查样地数据和2007年2月获取的Landsat TM影像数据，采用序列高斯协同模拟方法，分别在30m×30m和270m×270m空间分辨率水平上模拟森林地上部分碳密度及其分布，并对模拟结果进行对比分析。结果表明：仙居县森林地上碳密度分布具有空间连续变异性，四周为高碳密度有林地集中区，中间大部分为低碳密度无林地集中区，抽样估计研究区域地上森林碳储量为5283789.63Mg。基于30m×30m分辨率的序列高斯协同模拟结果为5692875.69Mg，模型确定系数为0.6203；对比270m×270m像元大小基础上估计得到的森林碳储量5030871.79 Mg ，模型确定系数0.2383，小尺度上估计的碳储量总量更多，碳密度分布范围更广，模型精度更高。序列高斯协同模拟考虑了森林碳密度空间分布的差异性，模拟结果接近地面样地估计值，碳密度分布范围合理，能够很好地反映碳分布空间的连续变异性。

关键词：碳储量；碳密度；碳分布；序列高斯协同模拟；多尺度

中图分类号：S757.2

文献标志码：A

文章编号：2095-1914(2015)02-0055-08

Abstract:Based on Forest Inventory (plot) data in Xianju County， Zhejiang in 2008 and the Landsat TM image data collected in the same region in 2007，the above-ground forest carbon density and its distributions at 30m × 30m and 270m×270m resolution was estimated and the results analyzed comparatively by applying sequential gaussian co-simulation The results showed that the above-ground forest carbon density of Xianju County was continuously distributed， which was surrounded by high carbon density of forest land and the intermediate region was filled with the majority of low carbon density of non-forest land. The total carbon is 5283789.63Mg based on the estimation by rardomly sampling method. With the sequential gaussian co-simulation， the sum of the carbon is 5692875.69 Mg and the square R of model is 0.6203 in 30m×30m resolution. Comparing with the result in 270m × 270m resolution， the former total carbon is larger， the range of distribution is wider and the model′s precision is higher. The result showed that sequential gaussian co-simulation which considers the spatial distribution of carbon density is closer to the estimation from the plot data， the carbon density distribution is more reasonable and the ability to represent the continuous changes of carbon distribution is better.

Keywords:forest carbon storage; carbon density; carbon distribution; sequential gaussian co-simulation; mutli-scale

收稿日期：2015-09-11

基金项目：福建省水土保持试验站“福建省水土保持林生态效益评价模型研究”资助。

doi:10.11929/j.issn.2095-1914.2015.02.010

Multi-Scale Regional Forest Carbon Density Estimation Based on

Sequential Gaussian Co-Simulation

SHEN Gao-yun1， ZHANG Mao-zhen1，2

(1.College of Environmental & Resource Sciences，Zhejiang A&F University , Lin′an Zhejiang 311300,China；2.Zhejiang Provincial

Key Laboratory of Carbon Cycling in Ecosystems and Carbon Sequestration，Zhejiang A&F University , Lin′an Zhejiang 311300,China)

区域森林碳分布作为森林生态系统研究和相关决策中的关键信息，近年来已成为森林生态学及其相关领域研究的热点[1]。目前，针对森林生态系统的植被碳储量和碳密度等进行了大量的研究[2-4]，但多数研究集中在森林整体碳储量估算方面[3-6]，有关森林碳分布的研究仍然很少[7]。及时准确地获取区域森林碳储量及其分布信息对评价森林CO2源汇能力具有重要意义[8]。

对于区域森林碳分布的估计是一个空间估计问题。传统的统计学提供了总体特征值的估计方法，随机抽样得到的结果只有总量估计值、估计值的方差和由方差计算的抽样精度，碳的空间分布状况无法获得。然而具有高精度的区域森林碳分布数据，对于森林资源管理、区域碳源汇评估、碳交易等有着十分重要的意义。地统计学通过其空间自相关理论提供了描述这些特征量空间分布的方法，在理论上解决了空间估计基础层面的问题[9]。近年来，土壤学、生态学等领域中对克里格插值(Kriging)与序列高斯条件模拟(sequential gaussian co-simulation，SGCS)进行了较多的对比研究[10-13]。分析结果表明，森林碳估计值是一个区域化变量，而克里格方法对其具有较强的平滑效应，普通克里格作为克里格插值方法的一种，也存在这一问题。而地统计学的空间随机模拟法能够克服克里格法的缺陷[14],它将数据作为一个整体来复原其整体的空间结构，追求的是模拟的真实性，尽可能地接近真实的空间分布，不像克里格方法，追求的是特定点位某个属性的局部最优估值[15-16]。同时，空间随机模拟还可直接用于空间不确定性研究，这也是克里格插值法欠缺的[17]。本研究以仙居县森林调查数据为依据，为比较不同尺度上估计结果的精度，分别在30m×30m和270m×270m尺度上利用序列高斯协同模拟对研究区森林地上部分碳储量和碳密度进行空间估计，并对照地面样地调查结果对模拟结果在空间上的差异性进行分析，进而做出评价。

1研究区概况

仙居县地处东经120°17′16″～120°55′51″，北纬28°28′14″～28°59′48″，浙江省东南部，位于浙江第3大水系——椒江水系的源头，东西长63.6km，南北宽57.3km。全县总面积2013.18km2。丘陵山地面积占总面积的80.6%，平原占11.1%。该县属典型的亚热带季风气候，温暖湿润，四季分明，年平均气温17.2 ℃，年均降雨量1444mm，年均蒸发量1190mm，年平均日照时数1786h。

根据2008年仙居县森林资源清查样地数据，全县林业用地面积1.64583×105hm2。林业用地中，有林地1.53369×105hm2(其中竹林面积占6.73%)，灌木林地6.289×105hm2，未成林造林地2.579×103hm2，无立木林地1.889×103hm2，森林覆盖率77.9%，森林总蓄积5.555×106m3。

2研究方法

2.1数据来源

2.1.1Landsat TM 遥感影像数据研究数据为2007年2月2日获取的Landsat TM影像，由于Landsat TM传感器第6波段为热红外波段，主要接收地物热辐射信息，所以常不被用于森林碳密度的估计，本研究采用TM 影像的6个波段，即波段1～5和7，空间分辨率均为30m×30m。首先对影像进行几何校正和辐射校正，在获得质量较好的影像基础上，提取样地位置所对应的6个波段影像亮度值，并进行不同的组合比值运算，在SPSS 20.0中进行相关性分析后,选取影像亮度值与样地实测碳密度值相关系数最高的波段4、5和7，用波段比值TM4/(TM5+TM7)参与序列高斯模型的模拟。

2.1.2地面抽样调查数据本研究采用2008年仙居县森林资源清查样地数据。该调查以整个县域范围为总体，按机械抽样方法，以2km×3km的网格间距设置正方形样地，样地面积为0.08hm2(28.28m×28.28m)。总样地302个，其中：有林地251个，占总样地比例的83.11%。

2.2数据预处理

2.2.1重采样为研究多尺度下森林碳密度的估计结果，参照MODIS影像最小空间分辨率250m×250m，将空间分辨率为30m×30m的Landsat TM影像重采样成270m×270m的模拟MODIS影像，与30m×30m分辨率原始影像共同作为不同尺度上碳密度估计研究的影像数据。

2.2.2样地森林碳储量估算通过地面302个有效样地的每木检尺记录，参考已有文献，用单株生物量模型计算样地单株地上部分生物量，累加获得样地森林总生物量，按照碳/生物量的平均转换系数0.5将样地总生物量转换为碳储量，即得样地森林地上部分碳储量，根据样地面积将其转换为碳密度[18]。

2.2.3数据正态分布性检验序列高斯协同模拟要求数据近似服从正态分布。通过研究区样地森林碳密度的频率分布直方图(图1)，可以检验数据是否服从正态分布。由于研究区样地森林碳密度数据不服从正态分布，因而对其进行立方根转换(图2)[19]，并剔除0值位置(无林木样地)，使其趋于正态分布。

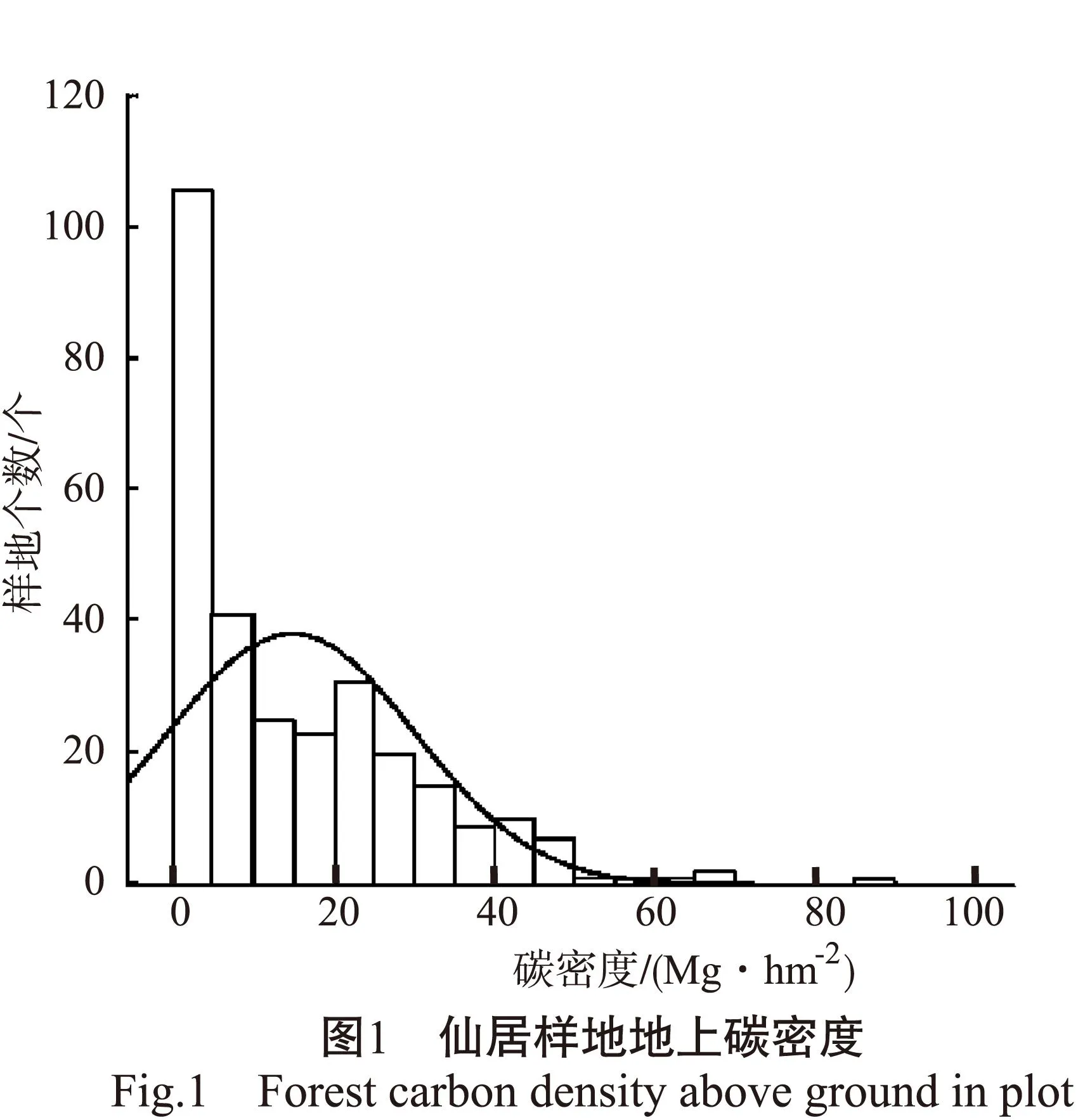
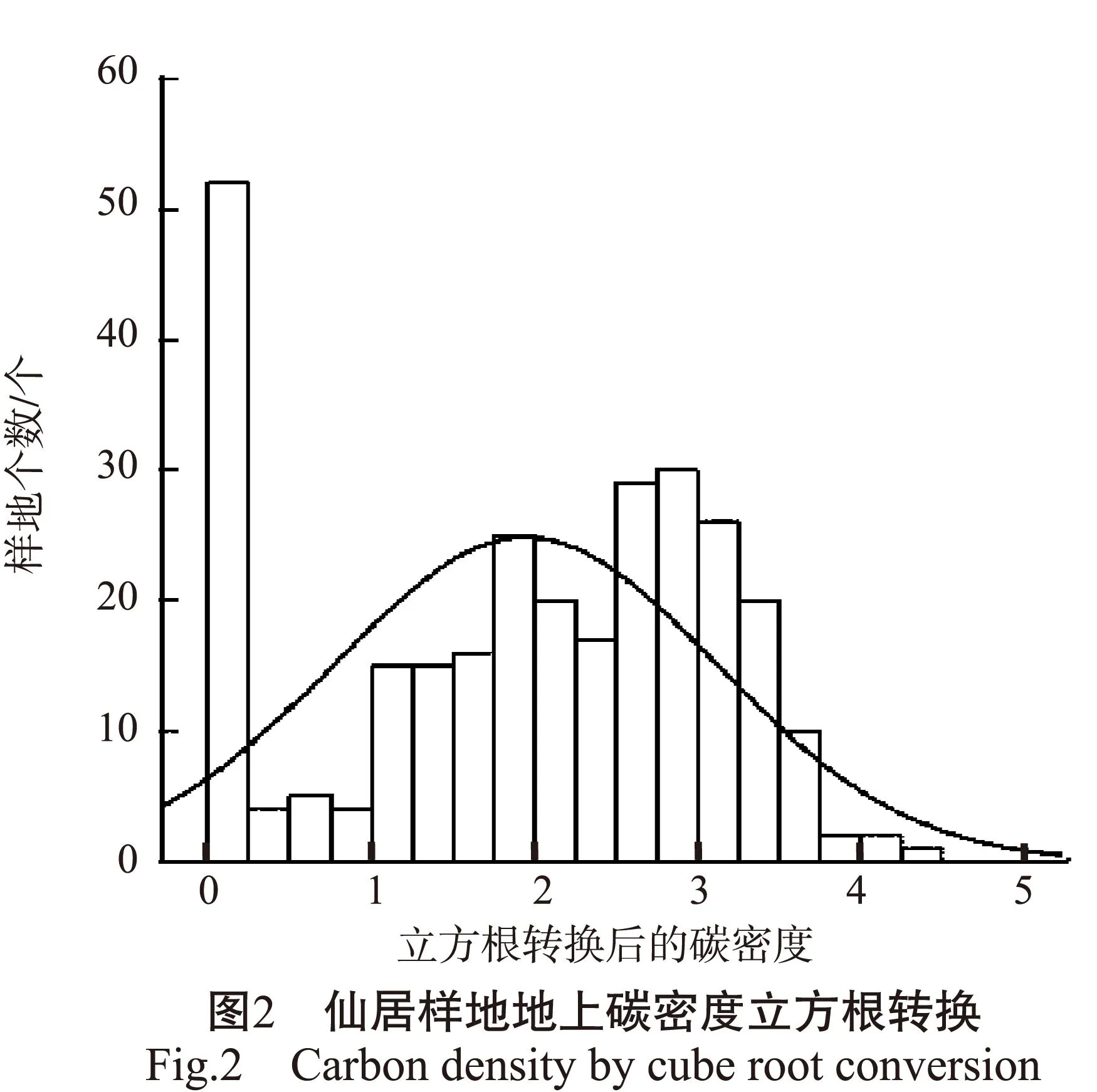
2.3森林碳分布估计方法

序列高斯协同模拟以研究区地统计变异函数为基础，结合地面样地和TM遥感数据，用随机模拟方法估计森林碳密度，即导出每个像元的森林碳密度估计值。

序列高斯协同模拟以Monto-Carlo方法为基础。用Monto-Carlo方法解算的一般过程是：首先，构建一个概率空间；然后，在该概率空间中确定一个依赖随机变量x(可以为任意维)的统计量g(x)，其数学期望E(g)=∃g(x)dF(x)正好等于所要求的值G，其中：F(x)为x的概率密度函数。统计量是样本x的函数，它不含任何未知量，一旦函数确定，可通过x的一系列观测值确定g(x)。

序列高斯协同模拟算法假设：每个像元的碳密度估计值是一个随机函数在该位置的随机变量Z(u)的实现，这个实现或估计值是从一个由周围的样地数据以及已有的估计值所确定的条件累积分布中通过随机抽样而获得，并假设这个分布是正态分布的，且被估计位置的遥感影像数据也被用来确定这个条件分布[8]。

典型的序列高斯协同模拟过程为：

1)随机选取第一个模拟值位置，以已知数据为条件，根据联合分布F(x)和Monto-carlo 方法算出该点的条件期望值。

2) 根据随机路径依次访问第u个格网点(u=1，2，…，m)，在第u个访问节点，根据前面的n个原始数据和前面(u-1)个访问节点获得的模拟数据建立条件概率密度函数。并根据条件概率密度函数，进行Monto-carlo随机模拟，随机产生该节点的一个模拟值。

3)重复第1)～2)步骤。直到所有节点均得到一个随机模拟值，最后获得整个研究区森林碳密度分布图。

4)将这一个过程重复执行L次，就可以得到L幅分布图，最后计算森林碳密度分布图的均值图[20]。

序列高斯协同模拟中训练样本选用经立方根转换后大致符合正态分布的所有有效样地碳密度数据(即保留0值样地数据)。该模拟中最重要的参数之一是变异函数，本研究采用VARIOWIN软件来分析样地森林碳密度。其Spherical标准化模型为：

γs(|h|)=0.63+0.37[1.5|h|/8198.63-0.5(|h|/8198.63)3]

式中：γs(|h|)为标准半方差；h为距离。

如图3所示。模型的变程为8198.63m。变程代表区域化变量空间自相关的最大距离。在此范围之内，观测值具有空间相关性，而在此范围之外，观测值在本质上相互独立。在序列高斯协同模拟过程中，以每个待估像元为中心的搜索半径大小可以参考变异函数模型中的变程值。

根据变异函数模型和地面样地地上部分碳密度，分别在TM影像像元30m×30m和270m×270m水平上进行序列高斯协同模拟，得到县域范围内森林碳密度及其分布。

3结果与分析

3.1多尺度序列高斯协同模拟与样地实测估计的对比分析

在不同尺度上，基于序列高斯协同模拟的森林地上部分碳分布见图4～5。

从图中可以明显地看出，研究区域周边森林碳密度值较高，中间区域偏低，与仙居县的地物分布特征一致。

图4中，影像像元大小为30m×30m，基于仿真模拟方法得到的研究区森林地上部分碳储量为5692875.69Mg，最大碳密度73.9782Mg/hm2，最小碳密度为0.0344Mg/hm2，平均碳密度为15.8850Mg/hm2，标准差为8.8878。

图5中，影像像元大小为270m×270m，基于仿真模拟方法得到的研究区森林地上部分碳储量为5030871.79Mg，最大碳密度54.0033 Mg/hm2，最小碳密度为0.4284Mg/hm2，平均碳密度为14.0378Mg/hm2，标准差为7.5184。

根据2008年仙居县县域范围内森林资源清查样地数据，按随机抽样的方法估计研究区域森林碳储量为5283789.63Mg，样地平均碳密度值为14.7435Mg/hm2，其最大值为86.9138Mg/hm2，最小值为0.0000Mg/hm2。从总体估计结果上看，虽然现有样地可以直接估计森林碳储量，但是随机抽样只能估计碳总量值，无法得到碳储量的空间分布，而序列高斯协同模拟能在考虑碳储量空间分布的基础上更好地估计森林碳储量。

现分别在像元大小30m×30m和270m×270m水平上对序列高斯协同模拟结果进行特征数统计，并与基于样地按随机抽样方法估计(抽样估计)的结果对比，结果见表1。

表1　2种分辨率下序列高斯协同模拟结果与实测数据

项目碳总量/Mg碳平均值最大碳密度最小碳密度(Mg·hm-2)准差(SD)仿真模拟30m×30m5692875.6915.885073.97820.03448.8878仿真模拟270m×270m5030871.7914.037854.00330.42847.5184抽样估计5283789.6314.743586.91380.000015.2728

由表1可知，像元大小为30m×30m影像上的估计结果和270m×270m影像上的估计结果在碳总量估计上分布于基于样地实测数据估计结果的两边。在以样地实测数据的估计结果为参照的基础上，30m×30m影像上的碳总量估计结果增加了7.74%，而270m×270m影像上的碳总量估计结果较参照值减少了4.79%。同时，两种尺度下的估计结果在最大碳密度上各自减少了12.9356Mg/hm2和32.9105Mg/hm2，又在最小碳密度上分别增加了0.0344Mg/hm2和0.4284Mg/hm2。

由此说明不同尺度下序列高斯协同模拟方法对研究区域森林碳密度分布范围的估计均有着不同程度的缩小。其中小尺度30m×30m分辨率上的碳密度估计范围变化相对较小，且总量增加，与实际较为接近，而大尺度270m×270m分辨率上估计的碳密度分布范围明显变窄，上限下移，下限上移，碳总量估计较实际偏小，这在一定程度上影响了碳密度空间分布的估计结果。这可能与原数据的分布状态有关，仙居县森林资源主要分布在四周的高山地区，中部集中了大量碳密度较小的无林区，使得在30m×30m分辨率上估计得到的碳密度分布变化程度较270m×270m分辨率上的突出，对空间连续变异更敏感。而且270m×270m分辨率的遥感影像是由小尺度30m×30m影像上的像元灰度值最邻近法插值而来，新产生的块内像素值受到了一定的“平滑”作用，使得估计得到的碳密度空间分布情况在整体上显得较为平坦，其反映无林地、非林地等无森林生物量地类空间分布的连续变化能力下降。总体而言，在小尺度上，序列高斯协同模拟的模拟结果能够更好地反应碳密度空间分布的连续变化情况。从表中还可以看出，序列高斯协同模拟在两种尺度上的标准差均与抽样估计的标准差15.2728相差较大，其主要原因是两种标准差计算的样本数不同，用于抽样估计的地面样地数大大少于像元数。

3.2多尺度序列高斯协同模拟与样地实测数据的对比分析

为了更加准确地判断序列高斯协同模拟方法在不同尺度上估计结果的正确性，现将碳密度估计结果与样地实测数据进行逐像元对比分析。分别将30m×30m和270m×270m分辨率下的序列高斯协同模拟碳密度估计图与样地碳密度实际分布图叠加，结果见图6～7。

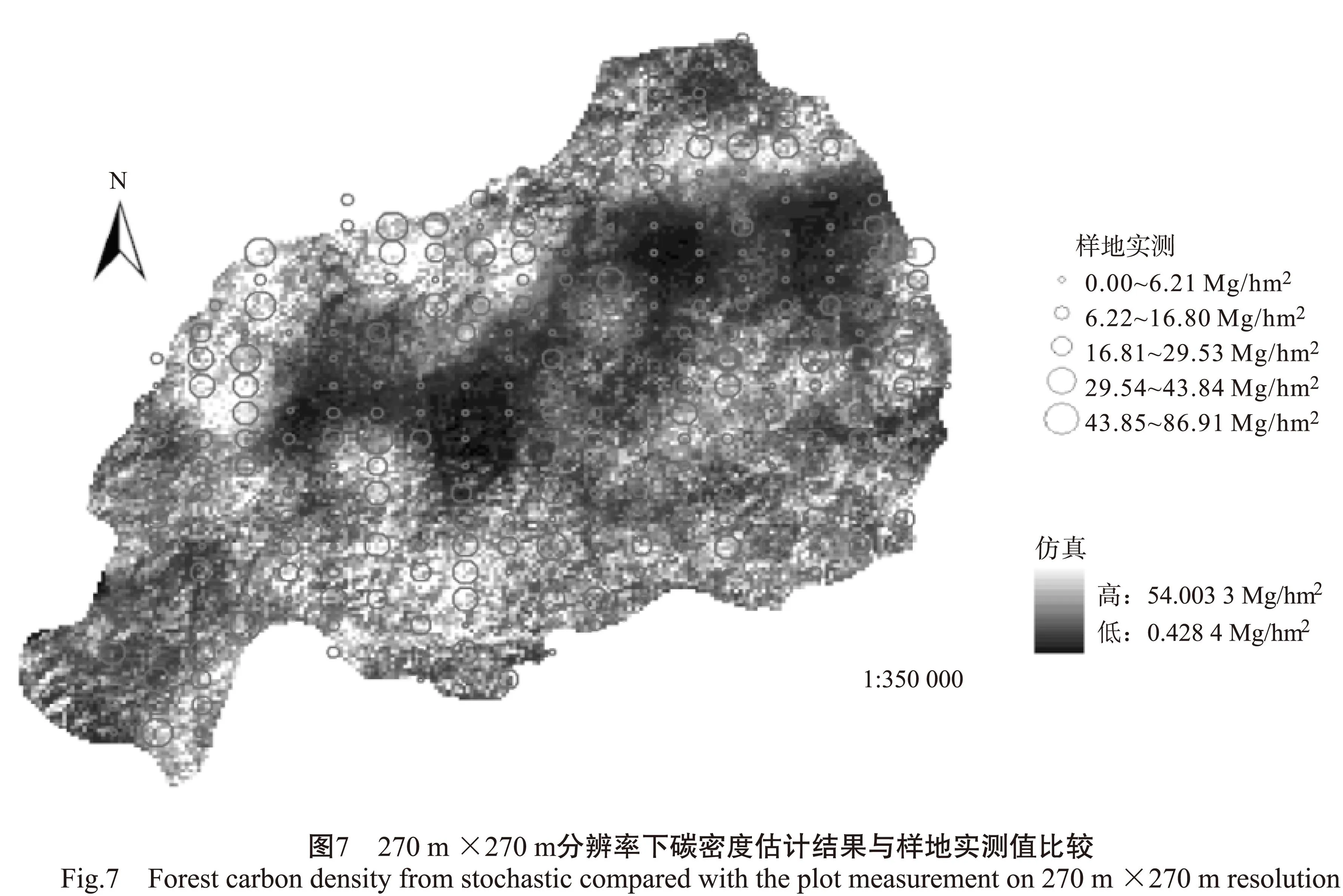
图中空心圆半径越大代表实测样地碳密度值越高，此时对应影像上的像素灰度值也普遍越高。因此,从图中可以看出,序列高斯协同模拟与样地实测碳密度数值有着很好的一致性，对于碳密度空间分布趋势的估计较符合实际情况，即碳密度较高的地区集中在仙居县周围的高山地区，碳密度较小的地区集中在仙居县中部人口密集区域。图例中还显示碳密度估计结果的值域范围，在30m×30m像元大小的影像下，序列高斯协同模拟估计的碳密度分布范围为0.0344～73.9782Mg/hm2。在270m×270m像元大小影像下的估计结果中碳密度分布范围为0.0428～54.0033Mg/hm2。小尺度上仿真模拟估计的碳密度区间跨度大于大尺度上仿真模拟结果，即随着尺度的增大，序列高斯协同模拟对于碳密度值分布连续变化的估计能力有所下降，区分程度降低。

提取样地点的仿真模拟估计数值，将其与地面样地实测碳密度值进行统计分析，以分析不同尺度下序列高斯协同模拟对森林碳密度估计的特点。以地面样地数据为参照值，分别对两种尺度下的估计结果进行比较，以离差平方和来反映两种估计结果与相同位置上地面样地数据的差异。结果见表2。

表2　2种分辨率估计结果与样地数据逐

表2显示，小尺度30m×30m影像下的仿真模拟结果在最大值与最小值之间的分布区间较大尺度270m×270m影像下的仿真模拟结果有明显上移。其差值平方和显示不同尺度上的估计结果有明显差异，小尺度上的仿真模拟相对于大尺度上模拟结果的RMSE更小，估计结果更接近样地实测值。

为了更好地对各模型进行对比分析，采用R2(确定系数)、SEE(估计值的标准误差)、MPSE(平均百分标准误差)。其计算公式如下[21-24]：

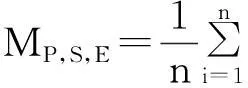
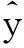
不同尺度下模型精度检验结果见表3。

表3　不同尺度下模型精度检验

从理论上讲，确定系数值越接近于1，标准误差和相对误差值越小，则模型的估计精度越高。因此，由表3可知，当尺度为30m×30m时，模型的确定系数为0.6203，尺度放大后，估计方法的确定系数变小，估计结果与样地实测值的拟合程度有所降低，而估计值的标准误与平均标准误差增大。说明像元大小为270m×270m时，估计量与其样地真实碳密度值的近似误差越大。原因之一是像元大小增大导致了块内像素值发生均值平滑。另外对原始TM影像进行非监督分类，计算整幅图像的林地平均斑块大小，得平均斑块面积为57018.9m2(约为238.8m×238.8m)，斑块大小小于270m×270m像元大小，地面破碎程度增大，从而导致误差增加。从标准差上看，小尺度30m×30m影像上序列高斯协同模拟估计结果的标准差为11.8707，与原始数据的标准差15.2738相比只低了3.4031，说明序列高斯协同模拟能较好地反映出研究区域实地碳密度分布的不确定性。在像元大小为270m×270m的估计结果中，序列高斯协同模拟的结果方差有所变小，说明尺度变大后，估计结果反映的区域碳密度分布情况更稳定，与实际的碳密度空间连续变化情况偏差变大。总体而言，序列高斯协同模拟能够在保证估计精度的基础上在小尺度上更好地保持全局的空间变异强度。

4结论与讨论

序列高斯协同模拟方法具有很好的空间格局重现能力，基于遥感影像数据和森林资源清查样地数据可以准确地获取较大区域内森林碳密度的分布情况。

序列高斯协同模拟结果精度随尺度增大、遥感影像分辨率降低而以较快速度降低。在小尺度上，序列高斯协同模拟的碳总体总量及空间分布更接近抽样估计结果，能够更好地反映碳密度空间分布。

像元大小由30m×30m转换为大尺度270m×270m后，采用序列高斯协同模拟方法估计的碳密度区间上限下移，分布范围明显变窄，总量估计值较小尺度呈下降趋势，对应样地估计值与样地实测碳密度值的拟合程度降低。通过最邻近法将遥感影像重采样成大尺度，像元值在一定程度上被平滑，使得估计结果呈现空间连续变异的能力降低，并且当地面破碎程度增大、斑块大小小于像元大小时，误差也会随之增加。总体而言，序列高斯协同模拟在小尺度上对碳密度空间分布和不确定性的估计有着明显的优势。

2种尺度上的序列高斯协同模拟估计均用到了样地实测数据与遥感影像数据。为了获得正确结果，需要地面样地与遥感影像有准确的位置匹配，而且所选特征的亮度值要与目标特征属性有一定关系[10]。而仙居县森林资源清查过程中，样地大小为28.28m×28.28m，而Landsat TM影像的分辨率为30m×30m，使得匹配存在误差，估计结果与真实值存在一定的偏差。

[参考文献]

[1]王效科，冯宗炜，欧阳志云．中国森林生态系统的植物碳储量和碳密度研究[J]．应用生态学报，2001，12(1)：13-16．

[2]Bartel P. Soil Carbon sequestration and its role in economic development: a donor perspective[J]. Journal of Arid Environments, 2004, 59(3): 643-644.

[3]王秀云，孙玉军．森林生态系统碳储量估测方法及其研究进展[J]． 世界林业研究，2008，31(5)：103-105．

[4]刘爽．森林生态系统碳储量研究进展[J]． 武汉生物工程学院学报，2009，5(3)：231-234．

[5]李克让，王绍强，曹明奎．中国植被和土壤碳贮量[J]．中国科学D辑，2003，33(1)：72-80．

[6]周玉荣，于振良，赵士洞．我国主要森林生态系统碳贮量和碳平衡[J]．植物生态学报，2000，24(5)：518-522．

[7]吴仲民，李意德，曾庆波，等．尖峰岭热带山地雨林C素库及皆伐影响的初步研究[J]．应用生态学报，1998，9(4)：6-9．

[8]张茂震，王广兴，周国模，等．基于森林资源清查、卫星影像数据与随机协同模拟尺度转换方法的森林碳制图[J]．生态学报，2009，29(6)：2919-2928．

[9]Wang R D. Linear geostatistics[M]. Beijing: Geological Publishing House, 1993: 123-163.

[10]Goovaerts P. Geostatistics for Natural at Resources Evaluation[M]. New York : Oxford University Press, 1997.

[11]Castrignanò A, Buttafuoco G. Geostatistical stochastic simulation of Soil water content in a forested area of South Italy[J]. Biosystems Engineering, 2004, 87(2): 257-266.

[12]赵永存，黄标，孙维侠，等．张家港土壤表层铜含量空间预测的不确定性评价研究[J]．土壤学报，2007，44(6)：974-981．

[13]Delbari M, Afrasiab P, Loiskandl W. Using sequential Gaussian simulation to assess the field-scale spatial uncertainty of soil water content[J]. Catena, 2009, 79(2): 163-169.

[14]Peter M, Cliftom A, Shlomo P. Effects of kriging and inverse modeling on conditional simulation of the avralalley aquifer in southern Arizona[J]. Water Resources Research, 1982, 8(4): 813-833.

[15]Zhu H, Journel A. G. Indicator conditioned estimator[J].Trans Soc Mining Engineering,1989, 286: 1880-1886.

[16]史舟，李艳，程街亮．水稻土重金属空间分布的随机模拟和不确定评价[J]．环境科学，2007，28(1)：209-214．

[17]柴旭荣，黄元仿，苑小勇．用高程辅助提高土壤属性的空间预测精度[J]．中国农业科学，2007，40(12)：2766-2773．

[18]沈希，张茂震，祁祥斌．基于回归与随机模拟的区域森林碳分布估计方法比较[J]．林业科学，2011，47(6)：1-8．

[19]金雨菲，张茂震，郭含茹，等．基于克里格插值与序贯高斯协同模拟的森林碳密度空间估计[J]．西南林业大学学报，2013，33(6)：32-37, 45．

[20]赵彦锋，孙志英，陈杰．Kriging插值和序贯高斯条件模拟算法的对比分析[J]．地球信息科学学报，2010，12(6)：767-776．

[21]Parresol B R. Assessing tree and stand biomass: A review with examples and critical comparisons[J]. Forest Science, 1999, 45(4): 573-593.

[22]Parresol B R. Additivity of nonlinear biomass equations [J]. Canadian Journal of Forest Research,2001, 31(14) : 865-878.

[23]曾伟生，骆期邦，贺东北．论加权回归与建模[J]．林业科学，1999，35(5)：5-11．

[24]Zabek L M, Prescott C E. Biomass equations and Carbon content of aboveground leafless biomass of hybrid poplar in Coastal British Columbia[J]. Forest Ecology and Management, 2006, 223(1/3): 291-302.

(责任编辑赵粉侠)

第1作者：张巧(1990—)，女，硕士生。研究方向：生态与环境。Email：geo_zq@163.com。

通信作者：黄义雄(1960—)，男，教授，硕士生导师。研究方向：景观生态学。Email：yxhuang@fjnu.edu.cn。