受转子位移激励的航空压气机呼吸裂纹叶片的联合共振

第一作者韩刚男，博士，1971年生

通信作者陈予恕男，教授，中国工程院院士，1931年生

受转子位移激励的航空压气机呼吸裂纹叶片的联合共振

韩刚，陈予恕

(哈尔滨工业大学航天学院，哈尔滨150001)

摘要：研究了航空压气机呼吸裂纹叶片在转子位移激励下的联合共振幅频响应的变化规律；叶片连续体模型采用伽辽金法简化成单自由度的系统模型，通过多尺度法导出了叶片在参数激励与位移激励联合作用下的共振幅频响应的一阶近似方程；分析了裂纹的开合深度、裂纹所在截面的位置以及转子在垂直与水平方向上的位移幅值差对幅频响应的影响；数值结果表明以上三个物理参数是促使叶片动力学行为发生变化的敏感参数，控制这三个物理参数的变化是有效防止叶片进一步破坏的根本途径。

关键词：压气机叶片；呼吸裂纹；联合共振；伽辽金法；多尺度法

基金项目：国家自然科学

收稿日期：2014-05-04修改稿收到日期：2014-09-03

中图分类号:O322文献标志码：A

Combination resonance of aero-engine compressor blade with a breathing crack under displacement excitation of rotor shaft

HANGang,CHENYu-shu(School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)

Abstract:The amplitude-frequency response of combination resonance of an aero-engine compressor blade with a breathing crack under the lateral displacement excitation of the rotor shaft was investigated. The blade was simplified into a single degree of freedom system using Galerkin’s method. The first order equation of the resonance response under parametric excitation combining with displacement excitation was derived by using the multi-scale method. The effects of the opening and closing depth of crack, the location of lateral section with crack and the displacement amplitude of rotor shaft on the amplitude-frequency response of resonance were analyzed. The obtained results show that controlling the changes of the above mentioned parameters which are of great influence on the dynamic behavior is an effective measure for preventing fatigue of the blade.

Key words:compressor blade; breathing crack; combination resonance; galerkin’s method; multi-scale method

航空发动机低压级叶片是发动机的重要部件，由于受多种动载荷的作用，极易产生疲劳裂纹，甚至导致破坏。在工程实践中，基于振动响应信号的裂纹无损检测技术的研究吸引了大量工程技术人员的兴趣。因此，带有裂纹的压气机叶片振动(线性和非线性)响应问题是近20～30年内理论研究的热点问题。通常为了理论计算、数值仿真以及实验研究的方便，压气机裂纹叶片被简化成带有横向裂纹的旋转悬臂梁模型。在裂纹叶片振动分析中, 目前存在两类裂纹模型: 张开(open)裂纹模型和呼吸(breathing )裂纹模型。大多数学者在研究中，为了简化计算通常忽略疲劳裂纹的非线性效应，而把裂纹看作张开裂纹考虑。然而真实的裂纹状态与其所受的动载荷有关，一般情况下裂纹并不是一直处于张开状态，是一种周期性张开-闭合的非线性过程。Gudmundson[1]试验中发现：使用张开裂纹模型计算结构频率，将会导致过低评估结构的损伤程度。

呼吸裂纹模型考虑了振动过程中裂纹张开—闭合的过程所带来的非线性动力特性，更符合实际情况。Shen等[2]采用双线性弹簧—质量振子模型，以及方波函数模拟呼吸裂纹梁的刚度变化过程，分析了系统在时域中的谱特性和频域中的谐波成分，该方法仅适用于结构外部激励频率较低时呼吸裂纹梁的动力学分析。Chondros等[3]考虑裂纹的开合作用，推导了裂纹梁的理论分析公式，分析了梁的低阶模态频率并与实验测量值进行比对，得到了一致的结果。Pugno等[4]根据周期性响应和裂纹连续张开、闭合的假设，定义非线性系统的代数方程，采用迭代求解方法得到裂纹梁的动力响应，分析了简谐载荷作用下含多个呼吸裂纹梁的非线性动力响应行为。Sunovsky等[5-6]提出呼吸裂纹梁的超谐波振动现象。然而，以上这些工作仅限于非旋转的简单裂纹梁动态响应的研究。

另外，由于压气机叶片处于高速旋转的工作状态，考虑转速对裂纹叶片非线性振动响应影响是必要的。Chen等[7]采用有限元模型研究了具有各向异性旋转裂纹梁的动态稳定性，讨论了旋转速度、局部刚度以及纤维方向对带裂纹的正交各向异性梁的静态屈曲载荷和动态不稳定域影响。Wu等[8]研究了带有横向裂纹的旋转梁动态行为，分析了不同转速情况下裂纹深度和位置对梁固有频率的影响。Akira等[9]采用频域/时域的多谐波混合方法分析裂纹叶片的强迫振动响应，讨论了裂纹长度和旋转速度对共振频率的影响以及在转速作用下裂纹几何尺寸变化，共振频率偏移和幅值多解引起的非线性突跳现象。

以上工作虽然研究了开-闭合裂纹叶片(或梁)的裂纹深度、位置以及转速对固有频率的改变规律，针对叶片(或梁)振动的时域信号谱分析给出裂纹叶片(或梁)强迫振动存在亚谐波、超谐波响应的非线性动力学现象，但是并没有详细分析特定工况下(受转子位移激励)裂纹(尺寸和位置)参数变化时，系统某一具体共振形式的幅频响应的变化规律。本文在前面提到的工作基础之上，采用呼吸裂纹模型，分析旋转呼吸裂纹叶片参数激励与外部激励(时变刚度和转子位移)联合作用下的共振幅频响应，讨论系统参数变化时联合共振幅频响应的演变规律。

1位移激励作用的无裂纹旋转叶片的运动方程

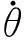
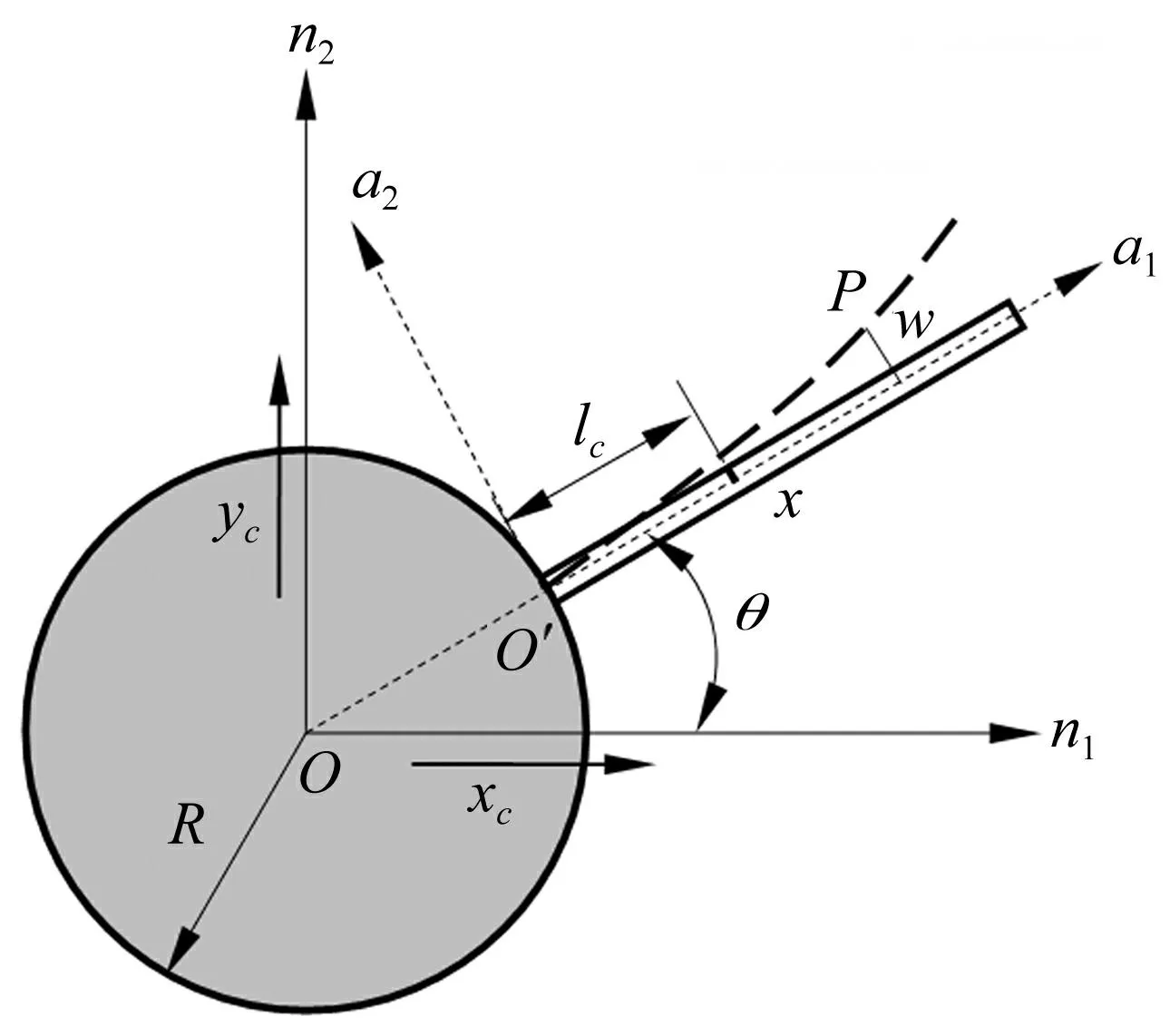
图1　裂纹叶片的力学简图 Fig.1 Sketch of the blade with a breathing crack

在平面运动时，变形后叶片的一点P的位移为：

yP=xcn1+ycn2+(R+x)a1+wa2

(1)

式中：x，w(x,t)分别为梁变形前P点的位置和变形后P点横向位移。

采用如下的坐标变换

(2)

P点的速度可以表示为

(3)

式中:“·”为变量对时间的导数。

叶片的动能可以表示为

(4)

式中:m为单位长度叶片的质量。

关于变形能的计算只考虑横向弯曲变形能，横向位移引起的轴向变形能以及离心惯性力引起的轴向变形能。

轴向应变为[10 ]：

式中：u(x,t)为叶片的轴向位移。“′”为变量对位置坐标x的偏导数。

在轴向应变的计算时，忽略相对横向位移较小的轴向位移u(x,t)以及较小的y·w″项，轴向应变可以近似为

(5)

横向和轴向变形能的和为

(6)

式中：E和I分别为叶片材料的杨氏弹性模量和叶片的截面的惯性矩。

离心惯性力为

(7)

离心惯性力引起的轴向伸长变形能为

(8)

实践表明，结构共振时共振模态起决定性作用，而其它模态影响较小。根据实际情况，我们认为系统的外激励频率应与系统第一阶模态频率相接近。为了简化计算，本文只考虑第一阶模态对裂纹叶片振动性态的影响，采用伽辽金法把叶片(悬臂梁)简化为具有集总参数的单自由度系统[11]。

设裂纹梁具有如下的振动形式：

w(x,t)=q(t)φ(x)

(9)

式中：φ(x)为一阶模态振型函数，q(t)为一阶模态坐标的位移函数。

为了得到系统的等效质量和等效刚度，假设一阶模态振型函数为[12]：

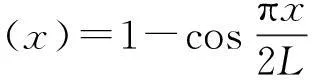
(10)

根据拉格朗日原理，推导系统的运动方程。拉格朗日函数为

(11)

把式(4)，式(6)，式(8)，式(9)，式(10)和式(11)代入下式

(12)

得到系统的运动方程为：

(13)

考虑到实际系统会受到阻尼的影响，在方程(13)中引入阻尼系数为c的粘性阻尼作用，把方程(13)改写为：

(14)

式中:

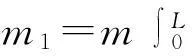
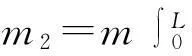
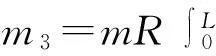
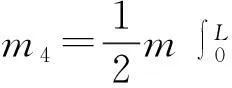
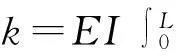
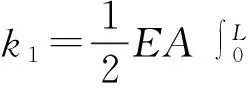
2位移激励作用的旋转裂纹叶片的运动方程

本文考虑的裂纹是一种呼吸裂纹形式，此裂纹有三种开—闭合状态：全开，全闭和半开半闭。因此呼吸式裂纹梁的刚度是由张开式裂纹刚度和闭合式裂纹刚度组合而成，刚度表达式为:

(15)

式中:kbr为呼吸式裂纹刚度；ko为张开式裂纹刚度；kc为闭合式裂纹刚度。当裂纹全闭时，kbr=kc=k。裂纹全开时，kbr=ko。F(t)为裂纹开闭合函数。

裂纹全闭时刚度为：

(16)

式中:Cc为裂纹闭合时梁的柔度。

裂纹全开时刚度为：

(17)

式中:Co为裂纹全开时梁的柔度。根据断裂力学理论Co=Cc+ΔC，ΔC为裂纹引入的附加柔度。它的表达式为[13]：

(18)

式中:αc=lc/L为裂纹所在横截面的无量纲位置。

φ=19.60α10-40.69α9+47.04α8-32.99α7+

20.30α6-9.98α5+4.60α4-1.05α3+0.63α2

α=a/B为裂纹的无量纲深度。E为杨氏弹性模量，ν为泊松比。

根据以上的论述，用裂纹的呼吸刚度kbr代替式(14)中刚度k得到呼吸裂纹梁的运动方程：

(19)

把xc=D1sin(ωt)，yc=D2cos(ωt)代入式(19)中，得到运动方程为:

(20)

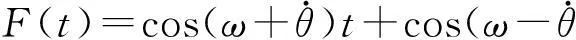
对式(20)进行无量纲处理，引入变量

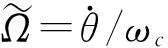
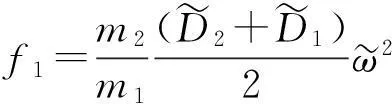
得到无量纲后的运动方程

f1cos(n1τ)+f2cos(n2τ)

(21)

3裂纹叶片的联合共振响应

从系统运动方程式(21)可知:系统可能存在多种复杂的联合共振响应。但是系统最终会出现什么样的联合共振响应，还要取决于实际的物理参数(例如模态频率和外激励频率等)。我们对实际叶片进行分析，认为系统极有可能出现外激和参激联合的一阶模态主共振的情况。

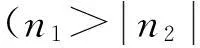
(22)

重新标度η→εη，γ→εγ，β→εβ，f1→εf1，f2→εf2，使阻尼项，非线性项以及激励项同时出现在一个摄动方程中。于是式(21)变为

(23)

采用多尺度法求式(22)的一阶近似幅频响应方程[15]。首先设

将式(22)、式(24)代入式(23)，令两端ε同次幂系数相等，得

(25)

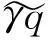
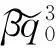
(26)

设式(25)的通解为

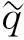
式中:φ=n0T0+φ(T1)。

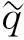
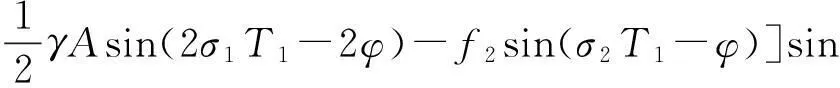
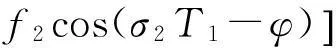
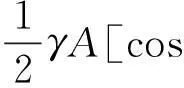
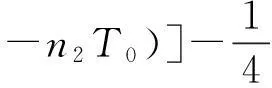
(27)

式中:A′，φ′分别为对T1的偏导数。

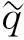
(28)

式中:θ1=σ1T1-φ，θ2=σ2T1-φ。

由式(28)可见，如果稳态解(A′=0)存在，则必有θ1和θ2等于常数，于是σ1=φ′=σ2。令θ=σ1T1-φ，改写式(28)为

(29)

对于稳态振动，A′=θ′=0。于是得到如下方程：

(30)

式(30)中两式两边平方相加，得

(31)

式(31)代入式(30) 的第二式，得

(1)平凡解，A=0。

(2)非平凡解A≠0时，A满足下式

(32)

4数值结果与讨论

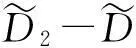
表1　叶片不变的物理参数

实际上，在方程(21)中参数激励幅值γ的大小与裂纹开合深度以及裂纹所在截面的位置是相关的。裂纹开合深度α越大，裂纹所在横截面位置αc越小(距离叶片根部越近)，参数激励幅值γ越大。

4.1裂纹深度对幅频响应的影响

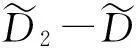
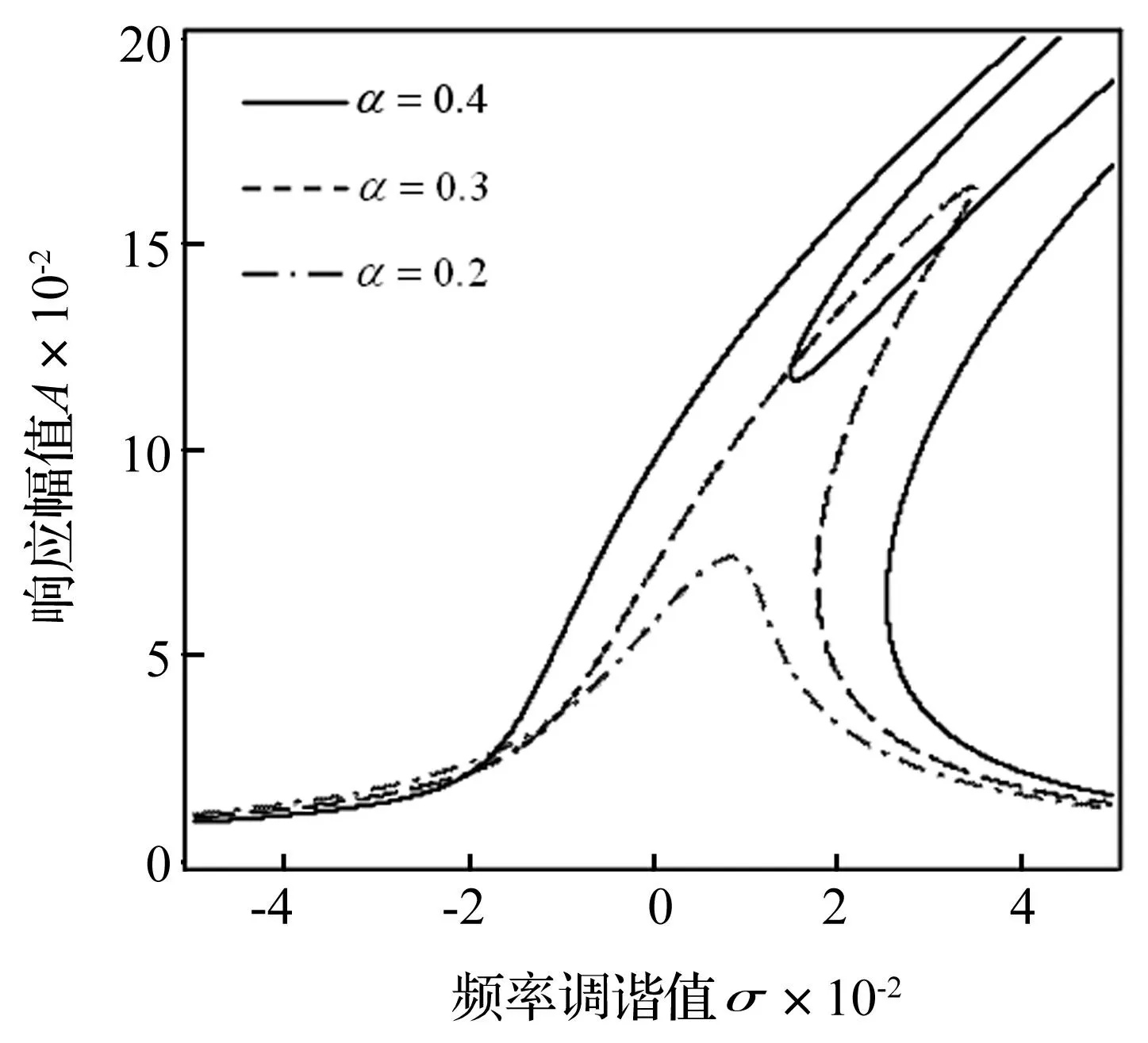
图2　随裂纹深度α变化的幅频响应 ( 1=0.000 5，α c=0.5) Fig.2 Amplitude-frequency response versus depth of crack α( 1=0.000 5，α c=0.5)

图3　随裂纹深度α变化的幅频响应 α( 1=0.000 5，α c=0.5) Fig.3 Amplitude-frequency response versus depth of crack ( 1=0.000 5，α c=0.5)

4.2裂纹位置对幅频响应的影响

为了考察裂纹所在横截面的位置变化对共振响应的影响。首先设转子的位移幅值差和裂纹在横截面内的开合深度为某一固定值，从而改变裂纹所在横截面的位置，分析其对幅频特性的影响。

4.3转子位移幅值差对幅频响应的影响

分为两种情况考察转子的垂直与水平位移幅值差对联合共振响应的影响。

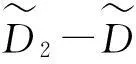
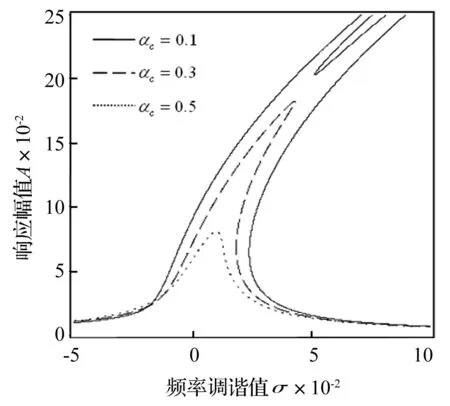
图4　随裂纹位置α c变化的幅频响应 ( 1=0.000 5，α=0.38) Fig.4 Amplitude-frequency response versus location of crack α c ( 1=0.000 5，α=0.38)

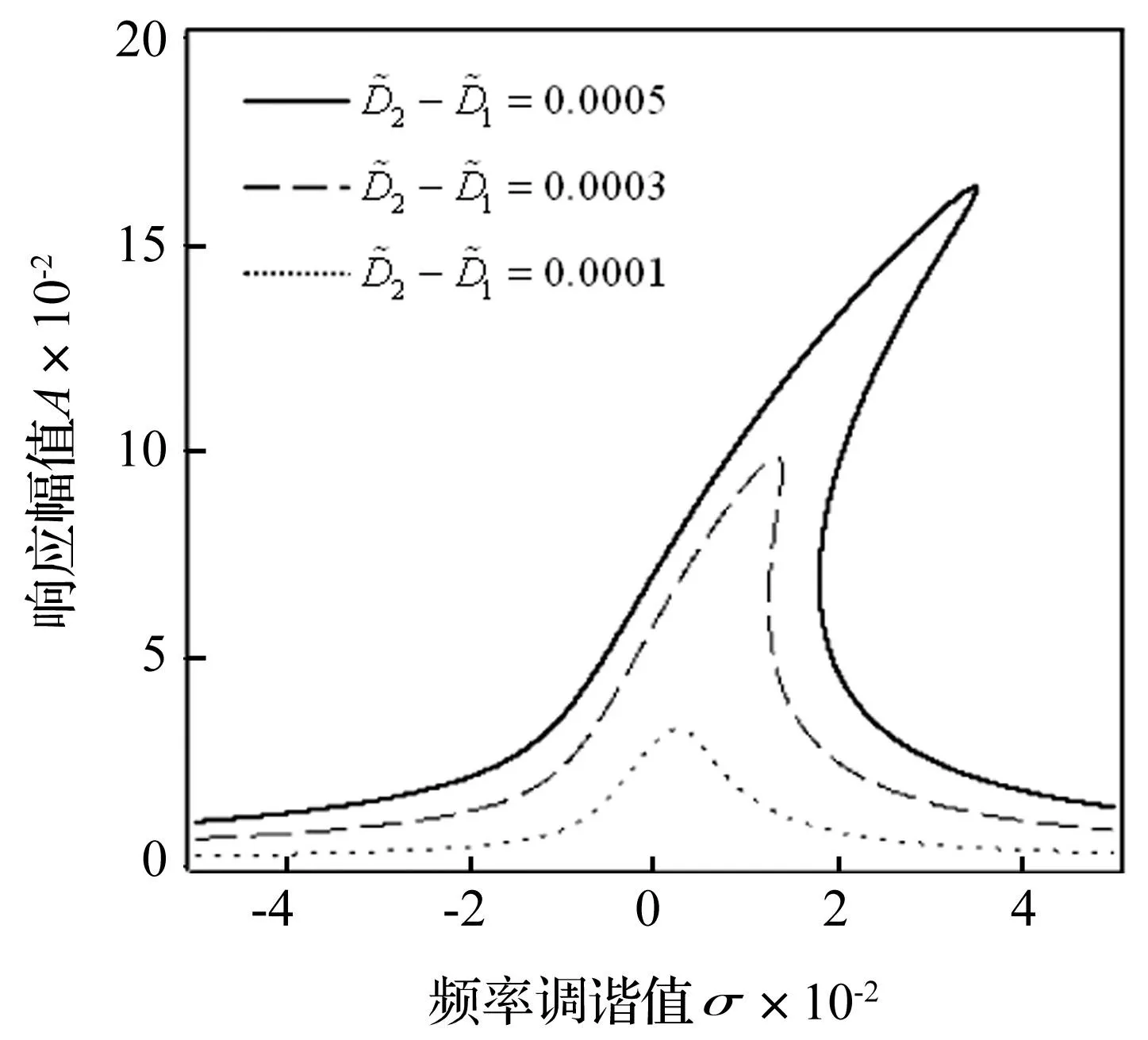
图5　随转子位移幅值差( 1变化的 幅频响应(α c=0.1,α=0.30) Fig.5 Amplitude-frequency response versus difference of displacement amplitude ( 1(α c=0.1,α=0.30)

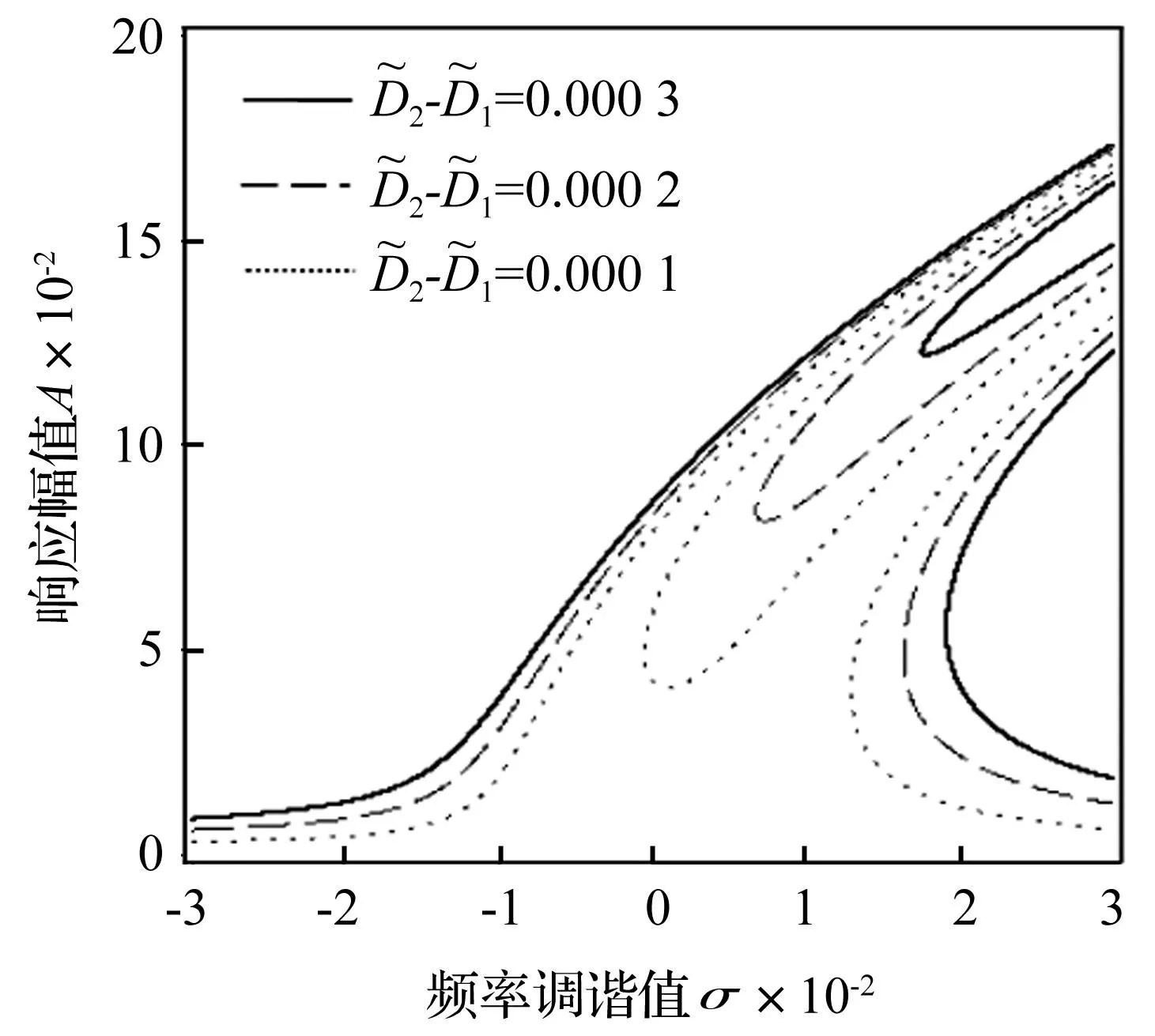
图6　转子位移幅值差 1变化的 幅频响应(α c=0.1,α=0.38) Fig.6 Amplitude-frequency response versus difference of displacement amplitude 1(α c=0.1,α=0.38)

5结论

裂纹的开合深度以及裂纹所在横截面的位置变化直接导致参数激励幅值的改变，从而使得幅频响应的幅值以及拓扑结构(滞后和分岔)发生变化。裂纹在横截面内的开合深度存在一个特定的分岔临界阈值，不同的横截面内分岔临界阈值不同。越靠近叶片根部的横截面内，裂纹开合深度阈值越小。这说明裂纹出现在叶片根部区域时，裂纹的开合变化对叶片振动性态影响较大，微小的改变会带来幅频响应的显著变化。

转子位移幅值差的变化仅仅改变幅频响应幅值的变化，而响应幅值的变化促使响应的滞后趋势发生变化。共振峰的分岔又仅取决于裂纹的开合深度以及裂纹所在横截面的位置(即参数激励幅值的大小)。共振峰分岔前，转子位移幅值差增加，响应幅值加大，滞后趋势增强。共振峰分岔后，转子位移幅值差增加使得幅频响应的分岔区域所对应的幅值逐渐上升到一个很高的水平，分岔区域对应的频率域远离线性共振频率点。以上的分析是假定裂纹的开合深度不随转子位移幅值差的变化而改变的。然而实际上，在响应分岔前，转子的位移幅值差增加使得响应幅值增加，而响应幅值增加会不可避免地使得裂纹持续开裂，最终导致响应分岔。导致转子幅值差变化的因素很多。例如在转子不平衡响应中，如果转子轴承间隙或刚度在方向上存在较大差异，那么必然导致转子在两个方向上的位移幅值差变大(椭圆轨迹变得狭长)，最终可能导致叶片的响应分岔。

对于裂纹来说，叶片的根部区域是一个敏感区域。此区域由于应力水平高，应力集中明显，又是裂纹极易萌生的区域。转子位移幅值差的变化又是促使裂纹开合深度变化的外在驱动力。因此尽可能地消除产生裂纹的外部因素，抑制裂纹的扩展，避免裂纹产生于叶片根部敏感区域以及控制可能引起转子振动位移幅值差变化的结构参数是叶片保持低幅值的、平稳的振动性态，有效地防止叶片进一步破坏的根本措施。

参考文献

[1]Gudmundson P. The dynamic behavior of slender structures with cross-sectional cracks[J]. Journal of Mechanics Physics Solids, 1983, 31(4):329-345.

[2]Shen M H H, Chu Y C. Vibrations of beams with a fatigue crack[J]. Computers & Structures, 1992, 45(1):79-93.

[3]Chondros T, Dimarogonas A, Yao J. Vibration of a beam with a breathing crack[J]. Journal of Sound and Vibration, 2001, 239(1):57-67.

[4]Pugno N, Surace C, Ruotolo R. Evaluation of the non-linear dynamic response to harmonic excitation of a beam with several breathing cracks[J]. Journal of Sound and Vibration, 2000, 235(5):749-762.

[5]Bovsunovsky A P, Surace C. Consideration regarding superharmonic vibrations of a cracked beam and the variation in damping caused by the presence of the crack[J]. Journal of Sound and Vibration, 2005, 288(4/5):865-886.

[6]胡家顺, 冯新, 周晶. 呼吸裂纹梁非线性动力特性研究[J].振动与冲击, 2009, 28(1):76-87.

HU Jia-shun, FENG Xin, ZHOU Jing. Study on nonlinear dynamic response of a beam with a breathing crack[J]. Journal of Vibration and Shock, 2009, 28(1):76-87.

[7]Chen Lienwen, Shen Gengshin. Dynamic stability of cracked rotating beams of general orthotropy[J]. Composite Structures, 1997, 37(2):165-172.

[8]Wu M C, Huang S C. On the vibration of a cracked rotating blade[J]. Shock and Vibration, 1998, 5(5/6):317-323.

[9]Saito A, Castanier M P, Pierre C, et al. Efficient nonlinear vibration analysis of the forced response of rotating cracked blades[J]. Journal of Computational and Nonlinear Dynamics, 2008, 4(1):011005.

[10]Arvin H, Bakhtiari-Nejad F. Non-linear modal analysis of a rotating beam[J]. International Journal of Non-Linear Mechanics, 2011, 46(6):877-897.

[11]Rezaee M, Hassannejad R. Free vibration analysis of simply supported beam with breathing crack using perturbation method[J]. Acta Mechanica Solida Sinica, 2010, 23(5):459-470.

[12]Dimarogonas A D, Paipetis S A. Analytical methods in rotor dynamics[M]. Elsevier Applied Science, London, 1986.

[13]Douka E, Hadjileontiadis L J. Time-frequency analysis of the free vibration response of a beam with a breathing crack[J]. NDT&E International,2005, 38(1):3-10.

[14]Cheng M, Wu J, Wallace W. Vibrational response of a beam with a breathing Crack[J]. Journal of Sound and vibration, 225(1):201-208.

[15]陈予恕. 非线性振动[M]. 北京:高等教育出版社, 2002.