基于自动搜峰瞬时频率估计的自适应多阶比分析技术研究

第一作者王栋男，硕士，中级工程师,1982年生

通信作者丁雪娟女，硕士，1986年生

基于自动搜峰瞬时频率估计的自适应多阶比分析技术研究

王栋，丁雪娟

(中能电力科技开发有限公司，北京100034)

摘要：提出一种利用自动搜峰的瞬时频率估计技术来实现旋转机械自适应多阶比分析(Adaptive Multiple Order Tracking, AMOT)的新方法。首先，通过时频分析得到振动信号的时频分布，根据频率峰值坐标自动选取搜峰起始点，自适应搜索出不同阶比分量的时频峰值。其次，利用最小二乘法将不同频率分量进行拟合实现瞬时频率估计，然后根据参考分量计算出重采样的鉴相时标对原始信号进行重采样，最后通过FFT变换实现阶比分析。该方法通过瞬时频率估计能够自动识别出所有阶比分量，实现优中选优，避免了传统算法中人为直观选取一个分量进行遮掩滤波提取分量的方法，减少了人为选取分量及起始点造成的误差，具有自适应性。并且无需同步采集转速信号，大大简化了应用条件，同时减少了人为因素，提高了分析精度，为旋转机械故障诊断提供了新方法。仿真实验和应用实例验证了方法的有效性。

关键词：故障诊断；自适应多阶比分析；瞬时频率；角域重采样

基金项目：龙源电力集团股份有限公司科技项目

收稿日期：2014-05-21修改稿收到日期：2014-08-19

中图分类号:TN911.6; TH115文献标志码：A

Tacholess adaptive multi-order tracking technology based on instantaneous frequency estimation with automatic peak search algorithm and its application

WANGDong,DINGXue-juan(Zhong Neng Power-Tech. Development Co. Ltd., Beijing 100034, China)

Abstract:A new method of adaptive multi-order tracking (AMOT) in rotating machinery was proposed based on the instantaneous frequency estimation with an adaptive peak search algorithm. The time-frequency distribution was obtained by using a certain time-frequency analysis method. According to the frequency peak coordinate, the starting point of peak search was selected automatically and time-frequency peaks of different orders were searched adaptively. The different frequency components were fitted to achieve the instantaneous frequency estimation by using the least square polynomial, and then the resampling time was calculated according to the reference component to resample the original signal. Finally multi-order tracking spectrums were obtained by FFT transform. By virtue of the method of instantaneous frequency estimation, the proposed method can automatically identify all-order components and choose the best one, avoiding the human error owing to choosing reference component and starting point subjectively in traditional algorithms. The method can identify the components of different orders without sampling synchronously the speed signal, greatly simplify the application conditions and improve the accuracy of analysis. It provides a new method for fault diagnosis of rotating machinery. The method was proved to be effective by simulation examples and practical applications.

Key words:fault diagnosis; adaptive multiple-order tracking; instantaneous frequency; angle domain resampling

旋转机械是工业生产中最重要的一类机械设备，广泛应用于电力、能源、矿山、冶金、国防等各个领域。为了确保旋转机械的安全平稳运行，状态监测与故障诊断技术得到了应用和发展。目前，基于振动信号的状态监测与故障诊断技术是最主要的方式。实际的振动信号一般都是非平稳信号，另外，旋转机械在启、停机和升降速的过程中表现为间歇性和非平稳性，包含丰富的故障信息。对于非平稳振动信号的处理，常规的信号处理方法往往失效，无法实现准确的故障诊断。

阶比分析是20世纪90年代发展起来的一种针对非平稳旋转机械振动信号的变频采样技术[1]。由于阶比分析在处理非平稳振动信号，尤其是处理转速变化时的振动信号方面的优势，对其研究得到了广泛的关注。目前，阶比分析技术主要分为两大类：一类是采用鉴相装置和转速计的硬件式阶比跟踪技术[2-3]，另一类是计算阶比跟踪技术[4-5]。对于硬件阶比技术，受到附加硬件及现场安装条件的制约，应用受到了限制。虽然计算阶比跟踪技术降低了对硬件的依赖，但仍然需要提供转速脉冲。

近年来提出的基于瞬时频率估计的阶比分析技术，根据频率和转速曲线的线性对应关系，完全靠软件来获得转速信息。通过时频分析方法获得信号的转速曲线，进而求得信号重采样的鉴相时刻，摆脱了阶比分析过程中对硬件的依赖，简化了阶比采样的实现要求[6-7]。文献[8]提出STFT-Viterbi拟合法进行瞬时频率估计，取得了一定效果。该方法需将频率范围分段，并给定参考轴转速。文献[9]提出改进的峰值搜索法，通过小波时频分布图进行峰值搜索，利用导数差值搜索峰值，避免虚假峰值，提高了瞬时频率的估计精度。但无法实现多阶比的自适应搜索。

本文提出一种基于自动搜峰瞬时频率估计的自适应多阶比分析(Adaptive Multiple Order Tracking，AMOT)新方法。通过自适应搜峰算法在振动信号的时频分布上得到多阶比的时频峰值频段，避免了人为因素的影响，能够自适应的选取起始点并根据判据条件自适应的提取出多个阶比分量。经最小二乘多项式拟合实现参考分量瞬时频率曲线拟合，计算信号重采样的鉴相时标，对原始信号进行角度重采样，最后进行频谱变换实现多阶比分析。仿真信号和实例信号结果均表明，该方法能够自动识别出不同阶比分量，具有自适应性，同时无需同步采集转速信号，简化了应用条件，可操作性强，为无转速计的阶比分析技术的在线监测应用提供了新方法。

1基于时频分析的自适应搜峰瞬时频率估计

阶比分析是将时域非平稳振动信号通过等角度重采样转换为角域信号获得阶比谱的一种信号分析方法。阶比能够很好地反映与转速相关的振动特征。对于非平稳振动信号，利用时频分析技术可以进行瞬时频率估计，进而得到鉴相信号，实现基于时频分析获取瞬时频率的无转速计阶比跟踪技术。

1.1瞬时频率

瞬时频率的概念具有一定的争议。原因有两个：一个是人们深受Fourier变换的影响，认为频率只能是用谐波函数在整个信号内定义。这样，瞬时频率的定义就和正余弦函数联系起来，当短于一个正余弦波形周期的频率是没有意义。另一个是瞬时频率没有统一的定义方法。直到应用Hilbert变换来构造解析信号时，解决了瞬时频率的统一定义问题。

给定信号x(t)，其Hilbert变换可以定义为函数x(t)与1/πt的卷积

(1)

式中：p.v.表示取积分的主值

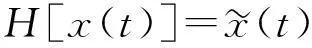
(2)

式中：

(3)

那么a(t)是z(t)的瞬时幅值，反映了信号能量随时间的变化情况。θ(t)是z(t)的瞬时相位。

理论上，可以有无数多种方法定义z(t)的虚部。而Hilbert变换用一种特别的方法来定义，通过这种方法来定义的虚部，z(t)能满足作为x(t)的解析信号的条件。由式(1)可以看出，Hilbert变换实际上是信号x(t)和1/t的卷积。因此，Hilbert变换可以表示x(t)的局部特性。式(2)的幅值和相位随时间变化，很好地表示了x(t)的局部特征。通过Hilbert变换，瞬时频率定义如下：

(4)

式(4)表明，瞬时频率是t的函数，任意时刻的瞬时频率只有一个值，只表示一个单分量频率。

1.2自适应峰值搜索算法

基于瞬时频率估计的阶比分析中，需利用原始信号估计参考轴转速。文献[8-9]利用峰值搜索法获得转速，并计算原始信号的时频分布图，对时频分布图一阶转速附近进行峰值搜索，将峰值时刻对应的频率视为该时刻转子的瞬时频率。但没有实现自适应多阶比分析。本文提出一种自适应多阶比分析算法，采用局部自动搜峰法，从最低频率开始自动搜索第一个阶比分量的时频分布峰值带宽，继续向上搜索，按照从低到高的顺序，依次搜索出所有阶比分量，具体算法为：在时频面上，设时频面的时间长度为N，频率长度为M，具体步骤描述如下：

(2)对nNB时刻(一般取中间时刻)这一列频率进行自动分段，即从最低频率开始，当出现连续f(nNB,mi)≥f0时，搜索出Q个频段，即，

Pj(nNB,hkj)=f(nNB,mi)

(5)

式中：Pj(nNB,hkj)为第j个阶比分量所包含的频率数组；hkj=1,…,kj;kj为阶比分量瞬时频率宽度，j=1,…,Q；Q为阶比个数；i=1,…,l1,l1+1,…,l1+k1-1,…,l2,l2+1,…,l2+k2-1,…,lQ,lQ+1,…,lQ+kQ-1。

Pj(nNB,hkj)=f(nNB,mi)具体表达式为：

(6)

(3)依次对每一个阶比带宽频率Pj(nNB,hkj)，j=1,…,Q，分别进行峰值搜索，得到相应的最大频率值，具体算法为：

(7)

其中：arg max表示取最大值；Pj(nNB,mMj)为最大频率峰值。

(4)从nNB时刻，改变时间ng,g=1,NB-1,NB+1,…,N。分别向两侧重复“(2)”逐列进行自动搜峰，得到所有时间列的阶比频率带宽。Pj(nNg,hkj)，为第g个时间列中，第j个阶比分量所包含的频率数组；hkj=1,…,kj;kj为阶比分量瞬时频率宽度，g=1,NB-1,NB+1,…,N；j=1,…,Q。

(5)对每一个阶比带宽频率Pj(nNg,hkj)，g=1,NB-1,NB+1,…,N，j=1,…,Q，分布进行峰值搜索，具体算法为：

(8)

式中：Pj(nk,mMj)为最大频率峰值，k=1,NB-1,NB+1,…,N；j=1,…,Q。

(6)最后得到Q个阶比分量峰值Pj(ns,mMj)，s=1,NB-1,NB,NB+1,…,N；j=1,…,Q。

自适应多阶比搜峰示意图见图1。

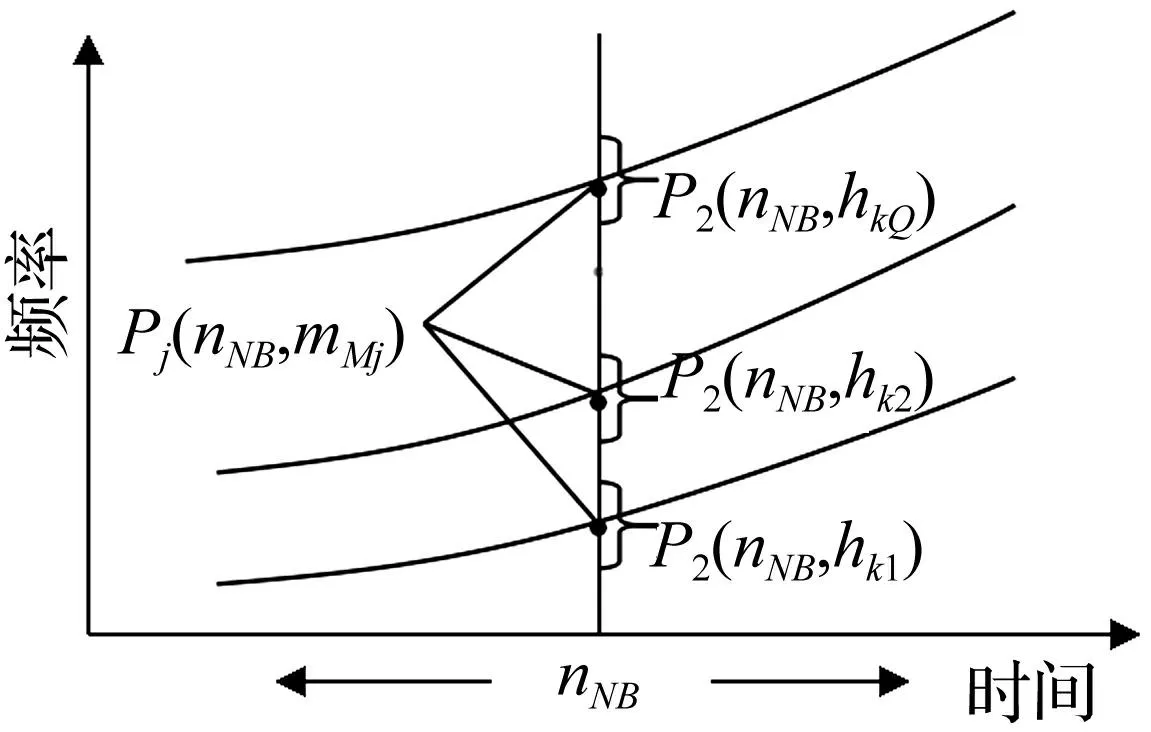
图1　自适应多阶比搜峰示意图 Fig.1 The sketch map of searching peaks adaptively for AMOT

2基于瞬时频率估计的自适应多阶比分析(AMOT)算法

基于瞬时频率估计的自适应多阶比分析(AMOT)算法流程图见图2。

AMOT算法具体步骤为：

(1)采用振动加速度传感器在被测齿轮箱上采集振动信号(无需同步采集转速信号)；

(2)对采集的振动信号进行加窗滤波处理；

(3)对初步处理后的振动信号进行时频分析，得到时频谱；

(4)采用自适应多阶比搜峰法，从最低频率开始自动搜索第一个阶比分量的时频分布峰值带宽，确定搜峰的起始点坐标，继续向上搜索，按照从低到高的顺序，依次搜索出所有阶比分量对应带宽及起始点坐标；

图2　基于瞬时频率估计的AMOT算法流程图 Fig.2 The flow chart of the AMOT algorithm based on instantaneous frequency estimation

(5)采用最小二乘方法拟合搜索到的所有阶比分量曲线；

对于给定的数据点(xi,yi),1≤i≤N，可用下面的n阶多项式进行拟合，即

(9)

为了使拟合出的近似曲线能尽量反映所给数据的变化趋势，要求在所有数据点上的残差都较小。

|δi|=|f(xi)-yi|

(10)

为达到上述目标，可以令上述偏差的平方和最小，即

(11)

这种方法称为最小二乘原则，利用这一原则确定拟合多项式f(x)的方法即为最小二乘法多项式拟合。

(6)根据瞬时频率的拟合曲线产生相应的鉴相时标Tn。

(12)

对于旋转机械升、降速阶段，若fi(t)满足光滑条件，在小范围内用拟合多项式或样条方程实现高精度逼近是可行的，因此若fi(t)=at2+bt+c。

则上式可以表述为

(13)

求解此方程的有效值，即可求得等角度采样的鉴相时标Tn。然后根据等角度阶比重采样时刻Tn，对初始等时间采样得到的信号进行三次样条插值以实现等角度阶比重采样，得到的角域周期循环平稳信号x(Tn)。

根据鉴相时标Tn对原始采样数据进行插值以实现信号的等角度插值重采样，进而得到所有阶比采样的角域离散转角序列x(Tn)；

(7)对离散转角序列x(Tn)进行FFT，得到全部的阶比分量。

3仿真实验

3.1仿真信号1

图3 x(t)的时域图Fig.3Thetimedomainwaveformofx(t)图4 x(t)的频域图Fig.4Thefrequencyspectrumofx(t)

图5为信号x(t)的STFT时频谱图，从图5可知信号所包含的频率分量以及其随时间变化的趋势。图6为采用本文提出的自适应搜峰算法的结果图，可以看出，仿真信号包含的两个分量均可以提取出来，图6(a)为低阶分量的瞬时频率曲线所对应的搜峰结果，图6(b)为高阶分量信号的瞬时频率曲线所对应的搜峰结果。对比图5和图6，直观上可以看出自动搜峰方法能够实现信号的搜峰过程，具有自适应性。图7(a)为对低阶分量的最小二乘的拟合过程，图7(b)为对高阶分量的最小二乘的拟合过程，从图7可知，最小二乘的拟合结果比较光滑，能够表现信号峰值的变化过程。通过对比理想曲线和拟合曲线可知，二者基本重合且具有较高的精度。

图5　信号的STFT时频谱图 Fig.5 The time-frequency spectrum of signal by STFT

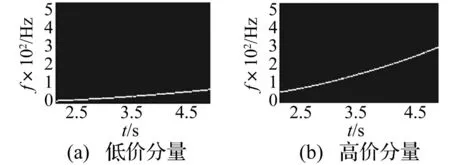
图6　AMOT自动搜峰结果 Fig.6 Theresults of AMOT automatic peak search

图7　分量的最小二乘拟合结果 Fig.7 The least square polynomial result of the component

以不同分量为参考分量进行阶比分析，图8为按照不同参考分量计算鉴相时标重采样后的角域图，可以看出信号比较平稳。

图8　重采样后的角域信号 Fig.8 Angle domain signal after resampling

图9为以两个分量分别为参考分量计算的阶比谱图，通过计算各个阶比分量的幅值关系，幅值较大的阶比谱图作为最后的显示分析结果，实现优中选优，避免了传统算法中人为直观选取一个分量进行遮掩滤波提取分量的方法，减少了人为选取分量及起始点造成的误差，具有自适应性。图9(a)中低阶分量为基频1阶，对应的高阶分量对应为4阶，两个分量的幅值与理想值非常接近。图9(b)中高阶分量为1阶，则相应的低阶分量为0.25阶，由于环节误差及能量泄露导致低频分量的幅值与理想值具有一定偏差。

从图9阶比谱图中能够清晰的显示出与基频分量相关的频率分量，与FFT频谱图形成了鲜明的对比，可以得出，阶比分析技术比较适合于分析变频振动信号，特别是频率随转速变化的变频振动信号。

图9　仿真信号1的阶比谱 Fig.9 The order spectrum of the first simulation signal

3.2升降速仿真信号2

为进一步说明算法的有效性，用旋转机械升速、平稳和降速的仿真实验信号进行阶比分析。仿真信号表达式如下：

y(t)=sin4πf(t)t+sin8πf(t)t+

sin12πf(t)t+sin2πf0t

(14)

式中：f0=6 Hz，t∈[2，7.913](s)，用以仿真旋转机械的低频共振。调频函数f(t)分为三段:第一段仿真旋转机械的升速过程，第二段仿真旋转机械的平稳运转过程，第三段仿真旋转机械的降速过程。其瞬时频率fi(t)定义如下：

(15)

图10为信号y(t)的时域图，用来仿真信号的升速、平稳、降速的过程。图11为信号的STFT时频谱图，很明显的可以看出该信号中有1阶，2阶，3阶分量，同时还有一个频率很低的直线。从图11可知,某一瞬时所对应的频率成分及其分布情况。

图10 y(t)的时域图Fig.10Timedomainwaveformofy(t)图11 y(t)的STFT时频图Fig.11Thetime-frequencyspectrumofy(t)bySTFT

图12～14图为自适应多阶比分析系统最后的显示结果，图12为自动搜索出来的第一阶分量，图13为重采样信号的角域信号，图14为按第一阶分量分析的阶比谱图，各阶分量的幅值谱都比较清晰，验证了方法的有效性。

图12 第一阶分量的峰值Fig.12Thepeaksresultofthefirstordercomponent图13 重采样角域信号Fig.13Theangledomainsignalafterresampling

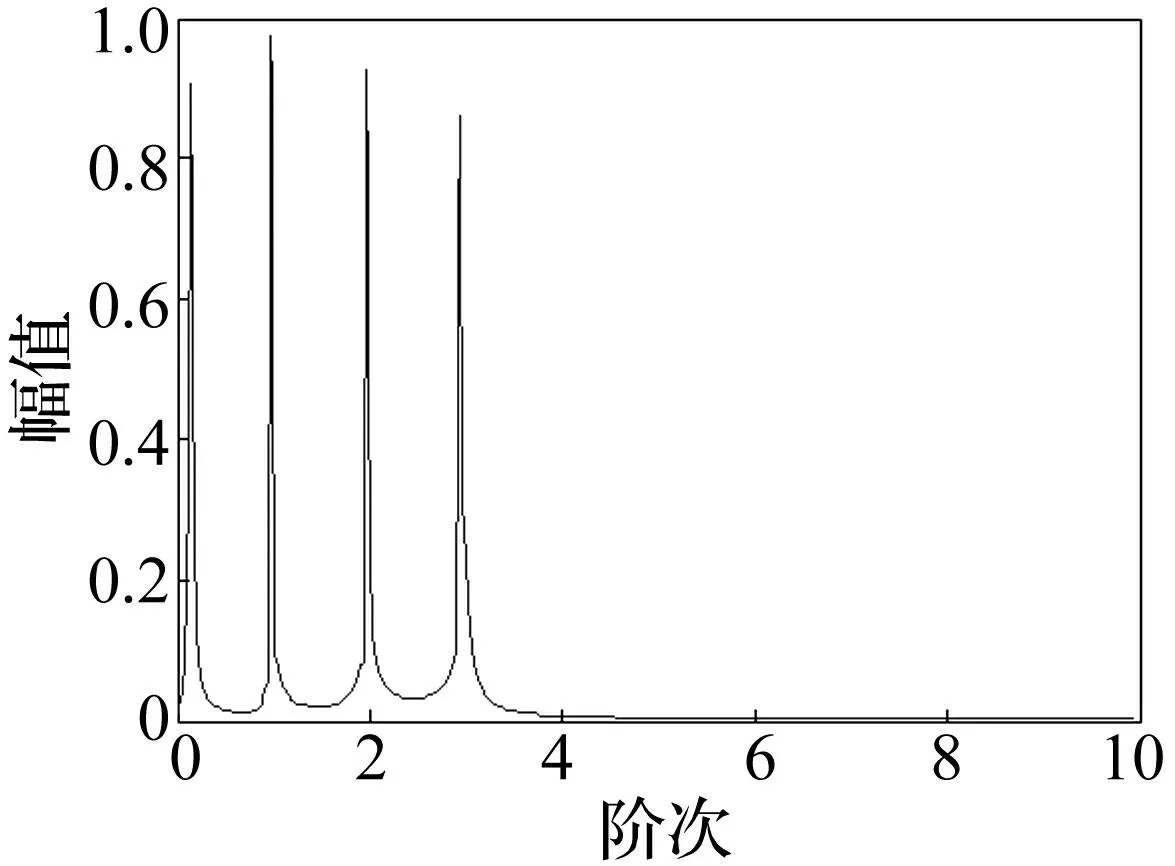
图14　仿真信号2的阶比谱 Fig.14 The order spectrum of the second simulation signal

4应用实例

某850 kW风电机组，齿轮箱结构由一级行星轮传动和二级平行轴传动组成。传感器测点布置位置见图15，齿轮箱高速端传感器布置实物见图16。

图15　传感器测点布置图 Fig.15 Measuring points layout of sensor

图16　高速端测点传感器布置图 Fig.16 The sensor layout of the high speed shaft

对机组高速端采集的振动信号见图17，采样率为2 500 Hz，采样时间为3.28 s，时域图中存在明显的冲击，但是不能判断故障类型及位置。通过本文提出的自适应多阶比方法分析得到时频图见图18，其中，自适应阶比分析方法展示的结果是以高速端转频的3倍频(图18中圈和箭头所示)作为参考频率进行分析，搜峰的结果见图19，图中X坐标为时间，Y坐标为频率，Z坐标为瞬时频率强度。经过最小二乘拟合得到图20，最后经过阶比分析得到阶比谱图21及其局部放大图22。从阶比图图21可知，高速端转频倍频现象明显，图中在3.574阶及其2倍阶附近均存在间隔为高速端转频的谐波分量，且高速端小齿轮与中速端小齿轮的啮合频率(8.965阶，约为高速端转频的25倍)较突出，其边频调制现象也较明显，边频带宽为高速端转频。图22将阶比谱放大(0～5阶之间，图21圈位所示)，观察低频段的频谱特征，存在高速端转频的1/3、2/3等倍频成分，根据齿轮的传动比关系，判断为中速轴的转频，其幅值较高，进而判断齿轮箱中速轴齿轮及高速轴齿轮存在损伤。图23为原始信号的频谱图，从图可知，图中存在谐波分量，但由于底部噪声较大，信噪比较低，信号特征频率的幅值较低，同时如图24，原始频谱图的放大效果显示(0～200 Hz之间，图23圈位所示)，在低频段的特征信息不明显。对比分析结果，可以看出本文提出的方法能够有效地实现齿轮故障的诊断。

图17 高速端振动信号Fig.17Vibrationsignalofthehighspeedshaft图18 高速端振动信号时频图Fig.18Thetime-frequencyspectrumofthehighspeedshaftsignal

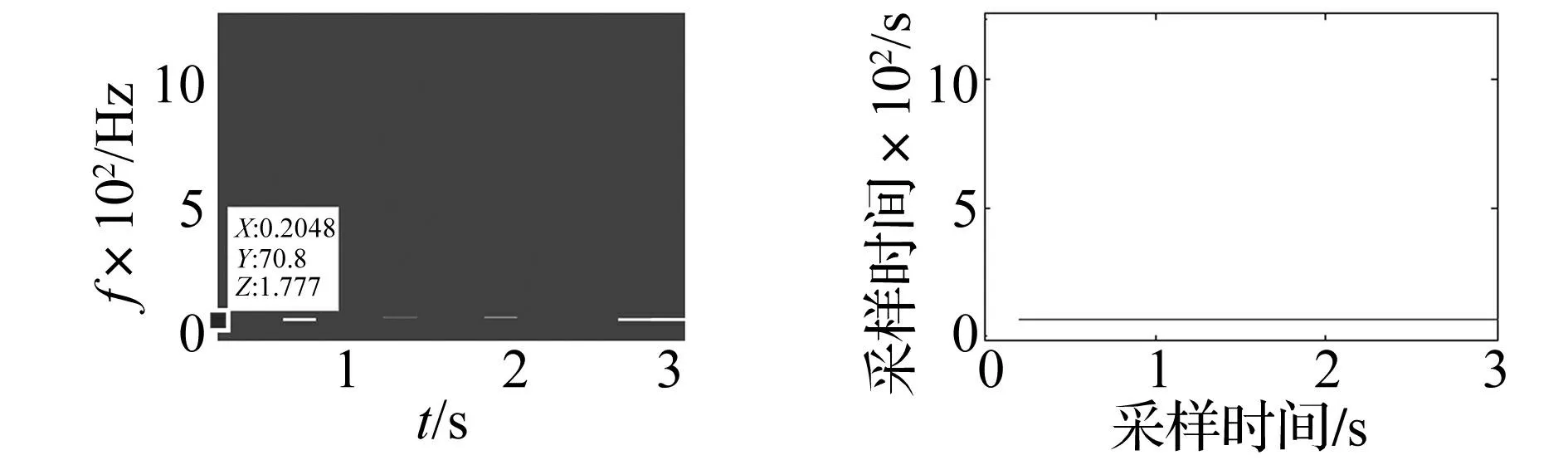
图19 阶比搜峰结果Fig.19Theresultsoforderpeaksearch图20 分量拟合结果Fig.20Fittingresultsofcomponent

图21　高速端振动信号的阶比谱 Fig.21 The order spectrum of vibration signal of high speed shaft

图22　高速端振动信号的阶比谱低频段局部放大 Fig.22 The order spectrum local amplification of vibration signal of high speed shaft

图23　高速端振动信号的原始频谱图 Fig.23 The original spectrum of vibration signal of high speed shaft

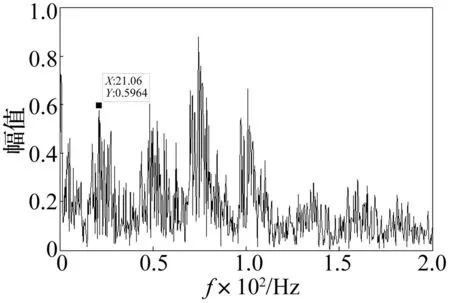
图24　高速端振动信号的原始频谱低频段放大图 Fig.24 The original spectrum local amplification of vibration signal of high speed shaft

经现场工程师登塔对齿轮箱进行内窥镜检查，如图25所示，高速端小齿轮存在明显的磨损和划痕(图25中左侧两个圈位所示)，中速端齿轮也存在磨损(图25中右侧圈位所示)，验证了方法的有效性。

图25　实际故障照片 Fig.25 The actual fault photos

5结论

提出一种用于提取旋转机械瞬时频率的自适应频率峰值搜索算法，在此基础上提出基于瞬时频率估计的无转速计自适应多阶比分析新方法。给出了算法的

步骤和实现过程。该方法无需同步采集转速信号，也不需要指定具体搜索阶比，能够自动识别出所有阶比分量。仿真信号和实例分析结果验证了方法的有效性。实例分析表明，所提出的自适应峰值搜索法能够有效提取出不同阶比分量，准确识别出风电机组高速级齿轮故障。

参考文献

[1]Potter R. A new order tracking method for rotating machinery[J]. Sound and Vibration, 1990, 24(9):30-34.

[2]Fyfe K R, Munck E D S. Analysis of computed order tracking[J]. Mechanical Systems and Signal Processing,1997, 11(2):187-205.

[3]郭瑜, 秦树人, 梁玉前. 时频分析阶比跟踪技术[J]. 重庆大学学报, 2002, 25(5): 17-20.

GUO Yu, QIN Shu-ren, LIANG Yu-qian. Order tracking method based on time-frequency analysis[J]. Journal of Zhongqing University, 2002, 25(5):17-20.

[4]赵晓平, 张令弥, 郭勤涛. 基于瞬时频率估计的自适应Vold-Kalman 阶比跟踪研究[J]. 振动与冲击, 2008, 27(12):32-36.

ZHAO Xiao-ping, ZHANG Ling-mi, GUO Qin-tao. Adaptive Vold-Kalman order tracking based on instantaneous frequency estimation[J]. Journal of Vibration and Shock, 2008, 27(12):112-116.

[5]杨志坚, 丁康, 杨茜. 基于频谱校正理论的阶比跟踪分析[J]. 机械工程学报, 2009, 45(12):41-45.

YANG Zhi-jian, DING Kang, YANG Xi. Novel method of order tracking analysis based on spectrum correction[J]. Journal of Mechanical Engineering, 2009,45(12):41-45.

[6]Blough J R. Development analysis of time variant discrete Fourier transform order tracking[J]. Mechanical Systems and Signal Processing, 2003, 17(6): 1185-1199.

[7]郭瑜, 秦树人，汤宝平,等. 基于瞬时频率估计的旋转机械阶比跟踪[J]. 机械工程学报, 2003, 40(9): 1648-1651.

GUO Yu, QIN Shu-ren, TANG Bao-ping, et al. Order tracking of rotating machinery based on instantaneous frequency estimation[J]. Journal of Mechanical Engineering, 2003, 39(3):32-36.

[8]赵晓平，赵秀莉，侯荣涛,等．一种新的旋转机械升降速阶段振动信号瞬时频率的估计算法[J]. 机械工程学报, 2011, 47(7):104-108.

ZHAO Xiao-ping, ZHAO Xiu-li, HOU Rong-tao, et al.A new method for instantaneous frequency estimation of run-up or run-down vibration signal for rotating machinery[J]. Journal of Mechanical Engineering, 2011, 47(7):104-108.

[9]胡爱军，朱瑜. 基于改进峰值搜索法的旋转机械瞬时频率估计, 振动与冲击, 2013, 32(7):113-117.

HU Ai-jun, ZHU Yu. Instantaneous frequency estimation of a rotating machinery based on an improved peak searchmethod[J]. Journal of Vibration and Shock, 2013, 32(7):113-117.