自振射流喷嘴腔内压力信号分析方法的研究

第一作者徐平平女，博士生，1982年10月生

通信作者马飞男，教授，博士生导师，1968年10月生

自振射流喷嘴腔内压力信号分析方法的研究

徐平平1，2，柳靖1，马飞1，汪晖1，蔡腾飞1,马琳1

(1.北京科技大学机械工程学院，北京100083; 2.内蒙古科技大学机械工程学院，包头014010)

摘要：喷嘴腔内流体的压力脉动与自振射流的特性密切相关，获取腔内压力信号并分析其构成对自振射流产生机理的研究具有重要意义。分别应用小波分析和希尔伯特-黄变换(HHT)对实测的腔内压力脉动信号进行对比分析，讨论了两种方法在压力信号提取和时频分析的适用性。结果表明：两种方法都能对腔内信号进行分解与重构，并能很好地提取信号的主要特征信息；HHT不存在基函数的预先选择，且经验模式分解(EMD)得到的本征模函数(IMF)分量能反映原始信号的固有特性，具有实际的物理意义；HHT可得到信号的瞬时频率，更有利于对腔内的脉动信号进行实时观测。相比于小波分析，HHT更适于自振射流压力脉动信号的分析与处理。

关键词：自振射流；压力脉动；信号分析；HHT；小波分析

基金项目：国家自然科学基金项目(51274021)

收稿日期：2014-11-12修改稿收到日期：2015-02-10

中图分类号:TV131.3+3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.17.030

Abstract:Flow pressure pulsation in a jet nozzle’s oscillation cavity is closely related to the characteristics of self-resonating jet. Composition analysis of the pressure signals is of importance in studying the generating mechqnism of self-resonating jet. Here, the pressure pulsation signals measured were analyzed with the wavelet analysis and Hilbert-Huang transformation (HHT) and their results were compared. The applicability of the two methods in pressure signal extraction and time-frequency analysis was discussed. The results showed that both two methods can be used in decomposing and reconstructing the signals in the cavity, the main feature information of the signals can be extracted well; there is no needs to pre-select the basic functions of HHT; the inherent characteristics of original signals can be reflected with intrinsic mode functions (IMFs) obtained from the empirical mode decomposition (EMD), they are of practical significance; the instantaneous frequencies of the signals can be gained from HHT, they are beneficial to the real-time observation for pulsation signals in the cavity; compared with the wavelet analysis, HHT is more suitable for analyzing and processing pressure pulsation signals in oscillation cavity of self-resonating jet nozzles.

Analysis methods for flow pressure signals in oscillation cavity of a self-resonating jet nozzle

XUPing-ping1,2,LIUJing1,MAFei1,WANGHui1,CAITeng-fei1,MALin1(1. School of Mechanical Engineering, Beijing University of Science and Technology, Beijing 100083, China;2. School of Mechanical Engineering, Inner Mongolia University of Science and Technology, Baotou 014010, China)

Key words:self-resonating jet; pressure pulsation; signal analysis; Hilbert-Huang transformation (HHT); wavelet analysis

自振射流是利用流体动力学、流体共振和水声学等原理而发展起来的一种兼有脉冲射流和空化射流特点的新型高效射流[1]。其作为清洗、切割、破碎工具具有独特的优越性[2]。自振射流的打击、破碎效果与振荡腔内流体脉动频率及振荡幅值密切相关[3-4]。对振荡腔内流动特征信号的提取和分析是进行自振喷嘴结构优化，进而实现对射流结构进行有效调制和控制的基础。

目前国内外在自振射流的研究中一般采用冲蚀、打击实验[5-8]，其本质上是对射流脉动特征的间接测试，无法区分喷嘴自身产生的自激信号、流体机械系统输入扰动与环境外扰。因此难以全面、准确地对喷嘴性能及相关影响因素进行分析与评估。

随着高频信号采集技术的发展，对自振喷嘴内部流动信号进行直接提取已成为可能。但是由于影响喷嘴内部流体运动的因素众多，信号来源复杂，如何对自振射流信号进行有效地提取、分析是急需解决的关键性问题。自振射流属于典型的非定常流动问题，流体动力参数在时域、频域上均发生剧烈变化，且信号成分复杂。而目前信号分析中普遍采用的快速傅里叶变换仅适用于平稳信号特征的提取，在处理自振射流问题时已不具备物理意义。小波变换能够同时提供信号在时域和频域的局部化信息，在诸多领域得到了应用。但其本质是窗口可调的Fourier变换，由于小波基长有限，因此在对信号进行时频分析时，会产生能量泄漏。

Huang等[9]提出利用经验模式分解(Empirical Mode Decomposition，EMD)和希尔伯特-黄变换(Hilbert-Huang Transform, HHT)分析非线性、非平稳信号的方法。HHT方法是一种全新的信号分析方法，能够描绘出信号的时频谱图、边际谱、能量谱等，是一种更具有适应性的时频局域化的分析方法[10-11]。它无需任何先验基函数，完全基于数据本身进行分解，得到的结果更具有清晰的物理意义和现实的适用性。该方法已在许多领域得到了不同程度的研究与应用。

本文将以实验数据为基础，深入分析小波分析和HHT分析两种信号处理方法在自振射流研究中的适用性。

1实验系统

自振射流实验系统见图1，实验系统由水箱、泵、流量计、蓄能器、喷嘴装置、传感器和数据采集系统组成。三柱塞泵提供的高压水通过系统管路进入喷嘴装置，通过电磁流量计检测系统中的流量，利用蓄能器吸收泵和管路的脉动，减少传感器采集到的信号中的干扰信息。实验中柱塞泵出水口压力可调。

1-水箱；2-过滤器；3-水泵；4-单向阀；5-溢流阀； 6-安全截止阀；7-蓄能器；8-流量计；9-压力表；10-喷嘴装置； 11-喷嘴固定支架；12-数据采集系统；13-计算机 图1　实验测试系统 Fig.1 The experimental test system

实验中以Helmholtz共振腔结构为基础，借鉴廖振方等的研究成果[12-13]，设计了如图2所示的喷嘴结构，其物理模型见图3。实验所选尺寸见表1。

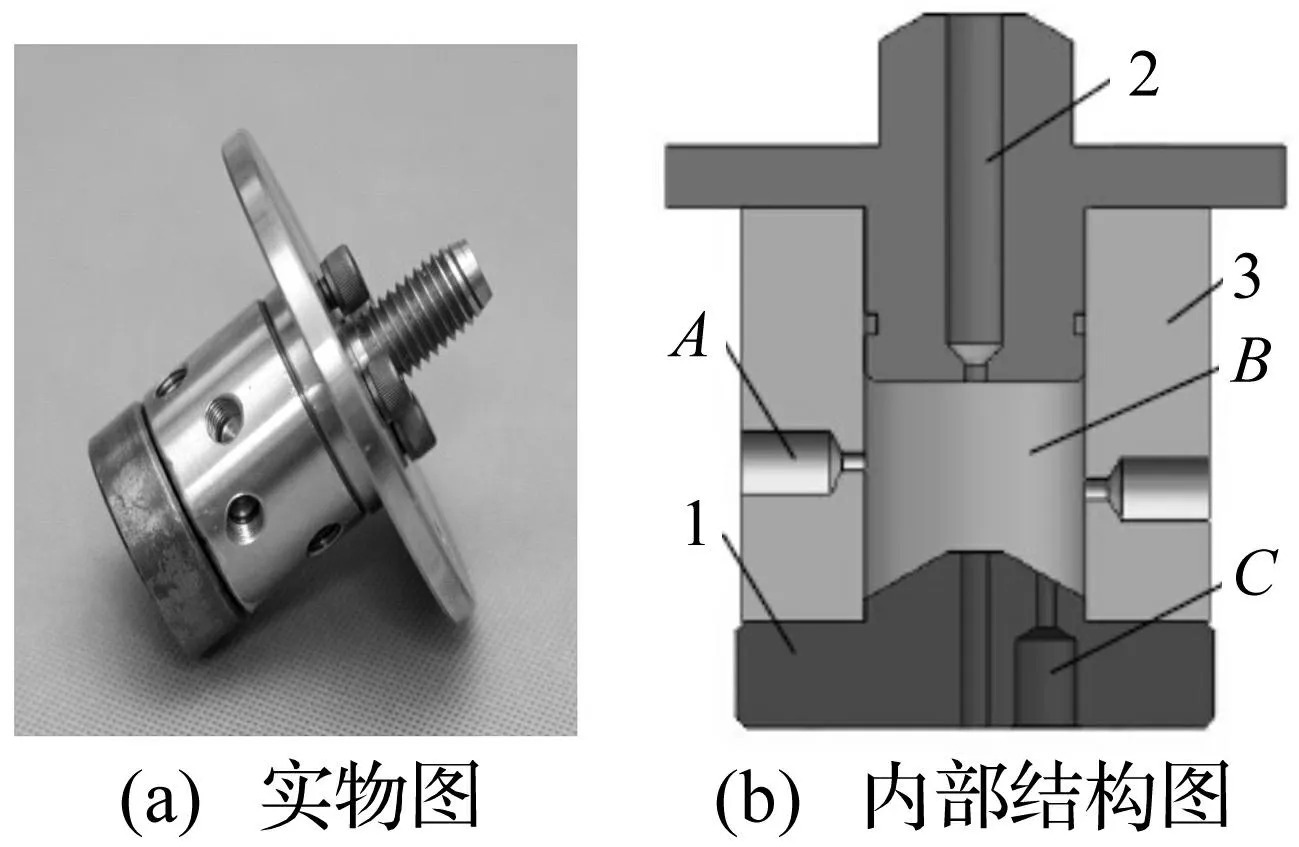
1-下喷嘴；2-上喷嘴；3-振荡腔体； A、C-传感器信号孔；B-振荡腔 图2　自振喷嘴结构 Fig.2 The structure ofa self-resonating jet nozzle

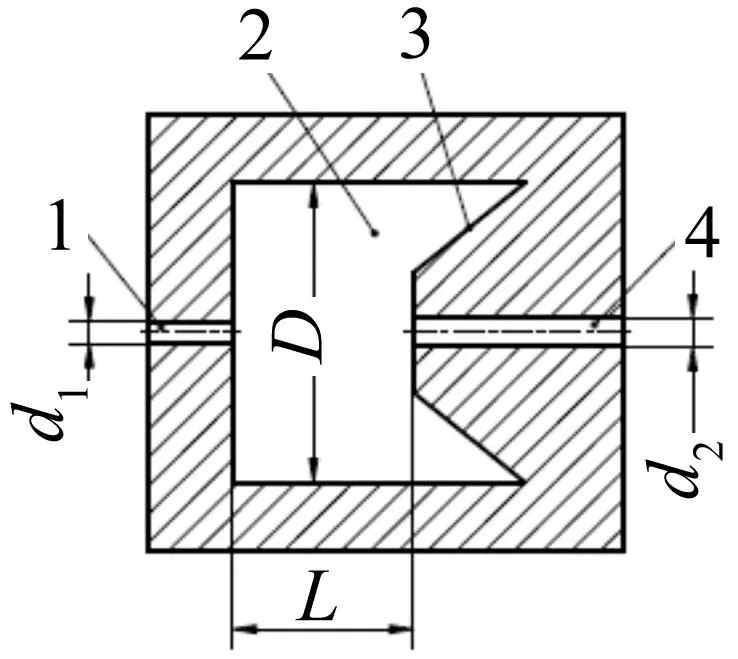
1-上喷嘴；2-振荡腔；3-碰撞面；4-下喷嘴 图3　自振喷嘴的物理模型 Fig.3 The geometric model of the self-resonating jet nozzle

入口直径d1出口直径d2腔径D腔长L1.11.3117.8

为了全面获取喷嘴腔内流体的压力脉动信号，在喷嘴装置腔内共布置9个压力测点。其中7个测点位于喷嘴振荡腔的壁面上，用于采集腔内径向压力信号；2个测点位于下游的碰撞壁面上，用于采集轴向的压力信号。传感器选用CYY8高频响压力传感器，量程0～7 MPa，测量精度为0.1%，动态频率响应最高为280 kHz。传感器采用嵌入式安装，与喷嘴装置螺纹连接。利用LMSSCADAS多功能数据采集系统对传感器拾取的压力信号进行采集与记录。图4为实验现场。

图4　实验现场 Fig.4 The experiments field

2信号分析方法

2.1小波变换

小波变换与傅里叶变换相比，它能够实现时域和频域的局部分析，即通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析，从而可以聚焦到信号的任意细节。平移因子可以改变窗口在相平面时间轴上的位置，而伸缩因子的大小不仅能影响窗口在频率轴上的位置，还能改变窗口的形状。小波变换对不同的频率在时域上的取样步长是可调节的，在低频时，小波变换的时间分辨率较低，频率分辨率较高；在高频时，小波变换的时间分辨率较高，而频率分辨率较低[14-15]。

2.2HHT变换

HHT变换主要有两步：EMD分解和Hilbert变换[16]。

2.2.1EMD分解

EMD分解过程就是个筛选过程，实现振动模式的提取。该方法的基本思路是用波动上、下包络平均值去确定“瞬时平衡位置”，进而提取出固有模态函数。上、下包络线由三次样条函数对极大值点和极小值点进行拟合得到的。

2.2.2Hilbert谱

EMD分解可得到所有可提取的固有模态函数。对固有模态函数进行Hilbert变换，可得到每个固有模态函数的瞬时频率，综合所有固有模态函数的瞬时频谱就可获得Hibert谱。Hilbert谱H(ω,t)可用下式表示信号：

(1)

其中，Re表示取实部；ai(t)为幅值函数；wi(t)为相位函数。

如果把Hilbert谱H(ω,t)对时间积分，就得到Hilbert边际谱：

(2)

边际谱提供了对每个频率的总振幅的量测，表达了整个时间长度内累积的振幅。

3喷嘴腔内压力信号小波变换和HHT变换

选取工作压力为5 MPa，腔长为7.8 mm，采样频率取5 120 Hz，通过实验得到了如图5所示的喷嘴振荡腔内的压力脉动信号。

本文将从不同角度分析小波变换和HHT变换对腔内压力信号进行分析处理的能力。

图5　原始的压力脉动信号 Fig.5 The original pressure pulsation signal

3.1分解与重构

小波分析中选用不同的小波基，得到的小波分量将有所不同，重构结果也有所不同，理论和应用都已有论证[15,17]。dbN小波系是工程上应用较多的小波函数，本文选用了db5小波对振荡腔内碰撞面上测得的压力信号进行了7层小波分解与重构，图6为小波分解重构后的结果。对信号经过小波分解后，可以生成不同尺度的细节图来反映信号的突变和瞬态特征。细节图中，d1～d4为信号的高频部分，d5～d7为信号的低频部分。

原始信号经EMD分解后的结果见图7。图中给出了9个IMF分量和趋势项r，每个IMF分量都具有不同时间特征尺度的振幅和频率，IMF分量按照频率从高到低来进行。由图8各分量的频谱图可以看出各IMF分量所包含的频率成分。EMD分解得到的IMF分量大都具有现实的物理意义。由IMF分量的幅值来看，IMF1、IMF2和IMF3幅值相对较大，IMF4～IMF9幅值明显减小。考虑到振荡腔内发生自激振荡时，压力信号脉动幅值较大，因此IMF1、IMF2、IMF3最有可能为流体自激所产生的信号分量。选用IMF1、IMF2和IMF3分量进行重构，可得到重构信号。

比较两种信号分解与重构的方法，小波分解存在着小波基的选取问题，不同的小波基，分解重构结果将有所差别，EMD分解直接从原始信号按不同的时间尺度分解出反映原始信号特性的IMF，不需要预设基函数。

3.2滤波与消噪

在进行信号采集时，由于环境噪声的存在，原始信号中都会含有或多或少的噪声。为了能够准确地分析信号中的有用信息，在对信号进行处理时，都要对信号进行必要的滤波或去噪。

小波变换具有时频局部化特性、多分辨特性和选基灵活性等特点，决定了小波消噪的有效性，即能够在去除噪声的同时，很好地保留信号自身的特征。小波消噪的基本步骤为：①选择合适的小波基，并对采集信号进行相应的小波变换；②小波分解系数的阈值化，对于每个小波系数，选择一个恰当的系数进行阈值量化处理;③信号的小波系数重构，得到去噪后的信号。

图6　小波分解各层细节信号 Fig.6 The layers details signal of wavelet decomposition

图7　EMD分解各IMF分量及余项r 9 Fig.7 The IMFs and remainder r 9 of EMD decomposition

图8　各IMF分量及r 9频谱图 Fig.8 Each spectrogram of IMFs and r 9

图9　小波去噪后的信号 Fig.9 The signal after wavelet de-noising

图9给出了采用db5小波基去噪的信号。由图可以看出，去噪后的信号比原始信号中的尖峰圆滑了很多，且保持了原信号的总体特征，这也表现出了小波变换在消噪中具有较好的性能。但是，从去噪后的信号特点上可以看出小波主要是对信号的高频进行去除，其中可能包含一些有用信号。由于振荡腔内的信号比较复杂，存在较多的扰动频率，利用小波方法，无法实现有用信号的提取，也就很难准确地将噪声进行去除。

EMD消噪方法就是利用分解得到的IMF分量进行信号重构，得到的去噪信号见图10。由于IMF分量具有实际的物理意义，EMD消噪可以去除一些相关性较小的信号成分，对有用的IMF分量进行提取求和。考虑到产生自激的情况，本文提取了前三个IMF分量，得到了去噪信号。比较EMD去噪信号与小波的去噪信号可以看出，EMD去噪信号中保留了原始信号的部分尖峰(如图中椭圆部分)，这也说明了小波去噪中将有部分有用的高频信号被去除，无法准确完整的反应原始信号中的有用信息。

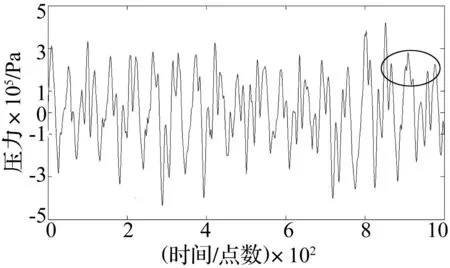
图10　EMD去噪后的信号 Fig.10 The signal after EMD de-noising

3.3时频分析

小波分析中的时频分析，能够较清晰地得到信号的频率成分，及各频率成分所包含的能量。

图11　小波分析时频亮度图 Fig.11 The time-frequency brightness figure by Wavelet analysis

小波分析的时频亮度图见图11。由图可以看出，主要的频率成分为100 Hz和300 Hz，其中100 Hz能量较高，且均匀分布于整个时域段，300 Hz能量断续分布。图12HHT时频亮度谱图显示瞬时频率较集中于100 Hz和300 Hz，相比较100 Hz密集，分布较广泛，300 Hz较为松散。比较两种分析结果，可以看出小波给出的频率成分较少，而HHT方法得到的时频亮度谱图，频率成分较多也较复杂，给出了信号的瞬时频率，表征了信号在每个时刻的变化情况。这主要是由于小波分析受测不准原理的限制，不能同时得到较高的时间和频率的分辨率，即在时间分辨率较高的情况下，频率分辨率相对较低，而HHT方法得到的瞬时频率可以将每一时刻的所有频率进行识别，能够实时准确地观察腔内流体扰动的变化情况。同时，通过HHT可得到图13所示的Hilbert边际谱图，该图能够清楚地给出信号的自振频率，以及该频率的能量值。

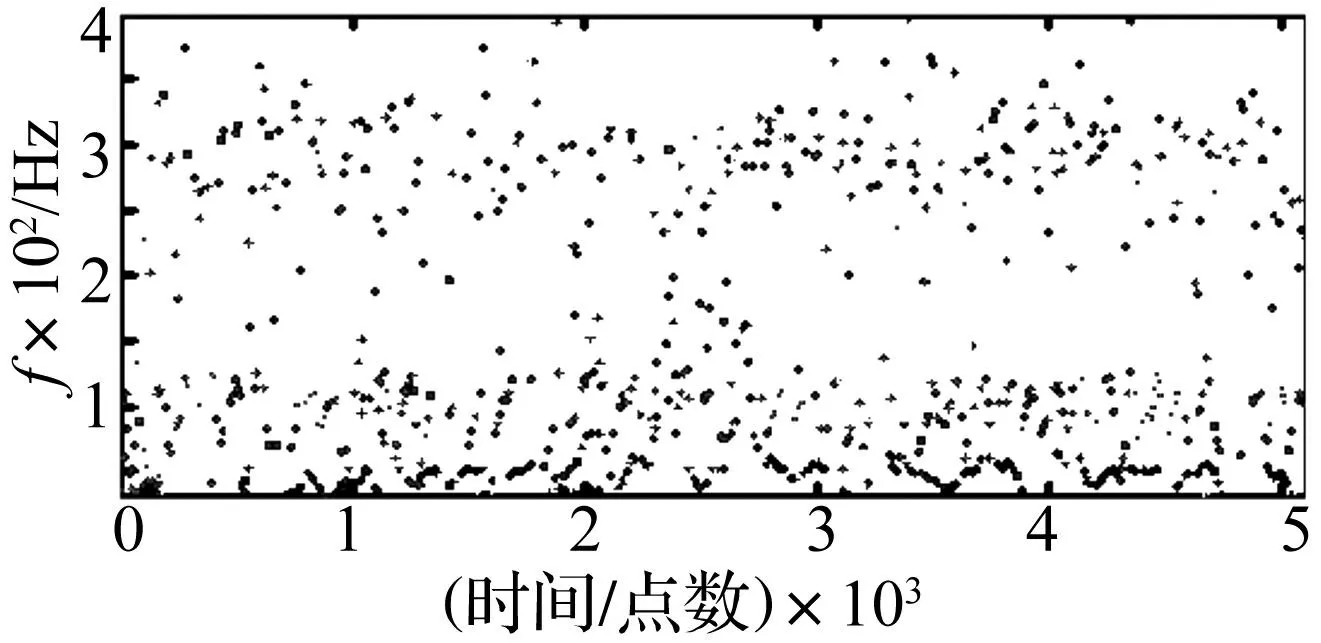
图12　HHT时频亮度谱图 Fig.12 The time-frequency brightness figure by HHT analysis

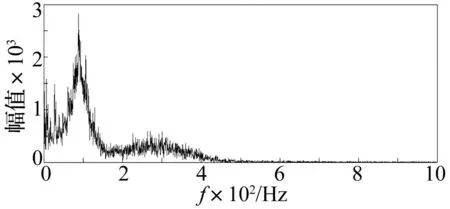
图13　Hilbert边际谱图 Fig.13 The Hilbert Marginal spectra

3.4突变信号点检测

当振荡腔内流体结构发生剧烈改变时，反映在压力信号中即表现为压力信号的突变。因此可以通过突变点的位置寻找流体自激振荡发生的时间节点，由图6的d3、d4和d5细节图，可以看出小波分解可以捕捉到压力信号突变现象。如d3放大的细节图中，1 900和2 300时间点的波形改变可以看做信号突变，但是其表现并不明显。而EMD分解得到的IMF分量(见图7)，特别是IMF1、IMF2和IMF3中，能够较清楚地看到信号突变的点。如IMF1中的1 900、2 000和2 300时间点等均出现了明显的信号突变。比较两种方法，EMD方法得到的IMF分量检测信号突变更明显更精细。

4结论

本文对比分析了小波分析和HHT变换两种信号处理方法在自振射流腔内流动信号处理中的适用性。研究结果表明：

(1)采用小波分析和HHT变换都能较好地对原始信号进行分解并重构，并能提取信号时域曲线的主要特征信息。但是，由于小波分析存在着小波基的选取问题，不同的小波基，重构结果将有所差别；而EMD直接从原始信号按不同的时间尺度分解出反映原始信号特性的IMF，不需要预设基函数，具有自适应和高效的特点。

(2)小波分析与HHT变换对振荡腔内压力信号都能进行消噪和滤波，小波方法保留原始信号近乎完整特征，但是由于其无法准确提取有用信号，消噪不够彻底准确；EMD方法能够提取了信号中的有用信息，在消噪和滤波方面具有灵活性和更强的适应性。

(3)虽然小波分析在一定程度上可以给出信号的时频特征，但受测不准原理的限制，不能同时得到较高的时频分辨率。而HHT方法可以得到信号的瞬时频率，更有利于对腔内的信号进行实时地观测。

参考文献

[1]廖振方, 唐川林. 自激振荡脉冲射流喷嘴的理论分析[J]. 重庆大学学报,2002,25 (2):24-27.

LIAO Zhen-fang, TANG Chuan-lin. Theory of the self-excited oscillation pulsed jet nozzle[J]. Journal of Chongqing University, 2002,25(2):24-27.

[2]Wang R H, Du Y K, Ni H J, et al. Hydrodynamic analysis of suck-in pulsed jet in well drilling[J]. Journal of Hydrodynamics, 2011, 23(1):34-41.

[3]杨敏官, 陆金刚, 王育立,等. 超高压水射流流场预测涡粘模型分析[J]. 农业机械学报, 2014,45(7):306-312.

YANG Min-guan, LU Jin-gang, WANG Yu-li, et al. Analysis of eddy viscosity models in predicting flow field of high-speed water jet[J]. Transactionsof the Chinese Society for Agricultural Machinery, 2014,45(7)：306-312.

[4]王萍辉,马飞. 自激振动空化射流振动分析试验[J]. 机械工程学报, 2009,45(10):89-95.

WANG Ping-hui, MA Fei. Vibration analysis experiment of self-resonating cavitating water jet[J]. Chinese Journal of Mechanical Engineering,2009,45(10):89-95.

[5]刘会霞,丁圣银,王宵,等. 水射流切割模型及其性能分析[J]. 农业机械学报, 2006, 37(11):122-124.

LIU Hui-xia, DING Sheng-yin, WANG Xiao, et al. Water jet cutting model and analysis of capability[J]. Transactions of the Chinese Society for Agricultural Machinery, 2006, 37(11): 122-124.

[6]李根生,易灿,黄中伟. 自振空化射流改善油层渗透机理及实验研究[J]. 中国石油大学学报:自然科学版,2007,31(1):72-76.

LI Gen-sheng,YI Can,HUANG Zhong-wei. Mechanism and experimental study of self-resonating cavitating jet for improving polluted rock permeability[J]. Priodical Office of China University of Petrolcum, 2007,31(1):72-76.

[7]李根生,沈忠厚,周长山. 自振空化射流冲击压力脉动特性实验研究[J]. 水动力学研究与进展, 2003,18(5):570-575.

LI Gen-sheng, SHEN Zhong-hou, ZHOU Chang-shan. An experimental study on impact pressure characters tics of self-resonant cavitating jets[J]. Journal of Hydro-dynamics, 2003,18(5):570-575.

[8]Guha A, Barron R M, Balachandar R. An experimental and numerical study of water jet cleaning process[J]. Journal of Materials Processing Technology, 2011, 211:610-618.

[9]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proceedings of the Royal Society of London, Series A,1998,454: 903-995.

[10]张俊红,王健,毕凤荣,等. 基于EMD和时频分析的低振动机体结构优化研究[J]. 振动与冲击, 2014,33(3):117-121.

ZHANG Jun-hong,WANG Jian, BI Feng-rong, et al. Structural optimization of a low-vibration block based on EMD and time-frequency analysis[J]. Journal of Vibration and Shock, 2014,33(3):117-121.

[11]汤宝平,何启源,蒋恒恒,等. 利用小波去噪和HHT的模态参数识别[J]. 振动、测试与诊断，2009，29(2):197-200.

TANG Bao-ping，HE Qi-yuan，JING Heng-heng，et al. Modal parameter identif ication based on Hilbert Huang Transform and wavelet de-noising[J]. Journal of Vibration, Measurement & Diagnosis, 2009，29(2):197-200.

[12]廖振方,唐川林,张凤华. 自激振荡脉冲射流喷嘴的试验研究[J]. 重庆大学学报:自然科学版,2002, 25(2):28-32.

LIAO Zhen-fang, TANG Chuan-lin, ZHANG Feng-hua. Experiments of the self-excited oscillation pulsed jet nozzle[J]. Journal of Chongqing University, 2002, 25(2):28-32.

[13]王循明.自激振荡脉冲射流装置性能影响因素数值分析及喷嘴结构优化设计[D].杭州：浙江大学, 2005.

[14]周福昌,陈进,何俊,等.基于小波滤波与循环平稳度分析的滚动轴承早期故障诊断方法[J]. 振动与冲击, 2006,25(4):91-93.

ZHOU Fu-chang, CHEN Jin, HE Jun,et al. Application of cyclostationary signal processing with wavelet filtering rolling element bearing fault diagnosis[J]. Journal of Vibration and Shock, 2006,25(4):91-93.

[15]李夕兵,张义平,刘志祥, 等. 爆破震动信号的小波分析与HHT变换[J]. 爆炸与冲击，2005,25(6):528-535.

LI Xi-bing, ZHANG Yi-ping, LIU Zhi-xiang, et al. Wavelet analysis and Hilbert-Huang Transform of blasting vibration signal[J]. Explosion and Shock Waves, 2005,25(6):528-535.

[16]杨宇,于德介,程军圣. 基于Hilbert边际谱的滚动轴承故障诊断方法[J]. 振动与冲击,2005,24(1):70-72.

YANG Yu, YU Dei-jie, CHEN Jun-sheng. Roller bearing fault diagnosis based on Hilbert marginal spectrum[J]. Journal of Vibration and Shock, 2005,24(1):71-72.

[17]张德丰. MATLAB小波分析[M].北京：机械工业出版社，2009.