鼓型消声器的声学性能计算与分析

第一作者赵晓臣男，博士生，1987年生

通信作者柳贡民男，博士,教授，1962年生

鼓型消声器的声学性能计算与分析

赵晓臣，柳贡民，张文平

(哈尔滨工程大学动力与能源工程学院，哈尔滨150001)

摘要：鼓型消声器是由膨胀腔和张紧的轻膜片构成。理论和实验研究表明，在空气输运系统中使用鼓型消声器能够在低频区域内取得较佳的降噪效果。使用Green函数和Kirchhoff-Helmholtz积分来计算矩形管道中膜片的辐射声场，进一步计算得到膜片振动引起的、作用在膜片上的辐射声压和消声器的传递损失。对比验证表明，所提出的解析法的计算结果和有限元仿真结果吻合良好。计算结果表明：通过简单地调节膜片的固有频率不能达到拓宽双腔并联鼓型消声器消声频带的目的；增大膜片和管道的距离将降低鼓型消声器的传递损失；将单腔鼓型消声器分为两个串联腔室后，可以通过长短腔室传递损失曲线的互补实现宽频降噪效果，并且每个膜片所需的优化张紧力下降，但是腔室分离之后低频消声效果将降低。

关键词：鼓型消声器；格林函数；消声特性；解析计算

收稿日期：2014-07-09修改稿收到日期：2014-08-29

中图分类号:TH212；TH213.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.17.026

Abstract:A drumlike silencer consists of an expansion chamber covered by light membranes under high tension. Theoretical and experimental study showed that introducing a drumlike silencer into a typical air conveying system can achieve a satisfactory quieting effect in a low-frequency region. Here, Green’s function and Kirchhoff-Helmholtz integral were used to solve the sound radiation of a membrane in a rectangular duct. After the vibration velocity of the membrane was obtained, the pressure perturbation induced by the membrane oscillation and the transmission loss of the silencer were calculated. The transmission loss calculated with the analytical method agreed well with that of the finite element method simulation. The results showed that simply adjusting the natural frequencies of membranes can’t broaden the acoustic attenuation bandwidth of the drumlike silencer with two parallel cavities; and the performance of the silencer may degrade when the distance between the membrane and the duct increases; when the single cavity of a drumlike silencer is divided into two tadem cavities, the TL curves induced by longer and shorter cavities can compensate each other and the broad band acoustic attenuation can be reached, the optimal tension for each membrane can also drop, but the acoustic attenuation performance within a low-frequency region declines.

Acoustic attenuation performance of a drumlike silencer

ZHAOXiao-chen,LIUGong-min,ZHANGWen-ping(College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China)

Key words:drumlike silencer; Green’s function; acoustic attenuation characteristics; analytical method

管道噪声的被动控制方法从机理上讲分为阻性措施和抗性措施。对于传统的抗式结构，声波在不同消声器元件的连接处由于阻抗不匹配而发生反射，从而使下游透射声能量降低[1]。但是传统被动消声元件多存在截面突变结构，从而造成较多的阻力损失。Huang[2-3]提出了一种新型的鼓型消声器(Drumlike silencer)，其通过沿管道流向平齐镶嵌安装的张紧膜片改变管壁阻抗，从而在管道通流截面不变的情况下向上游反射声波，理论分析[4]和实验[5]表明，该类型消声器在使用优化后的膜片质量和膜片张紧力的情况下，在膨胀腔消声器消声性能曲线的前两个衰减拱形域的频率范围内消声效果大大优于膨胀腔消声器。

1单腔室鼓型消声器分析方法

1.1单腔室鼓型消声器计算模型

单腔室鼓型消声器的模型见图1(a)，两个张紧的膜片将膨胀腔消声器的腔室和主管道分离开，从而构成了鼓型消声器。若两个膜片完全相同时，由于结构的上下对称性，则可以只考虑消声器的上半部分区域，见图1(b)。对于矩形管道中的鼓型消声器，当侧边张紧力不大时，三维声学计算结果和二维计算结果差别不大[15]。因此，本文只建立了该消声器的二维计算模型。

图1　单腔室鼓型消声器模型(一半) Fig.1 The drumlike silencer with a single cavity (a half)

整个消声器的内部结构形状类似于一个简单膨胀腔，管道高度为2ha，膨胀腔高度为hb，膨胀腔长度为L。沿管道方向平齐装有张紧的膜片，膜片把流体区域分割成两个部分：外侧的腔室流体域和内侧的主管道流体域。主管道侧流体域的声速为c0，密度为ρ0，腔室侧流体域的声速为c1，密度为ρ1。

膜片和膨胀腔外壁构成的b空间内的声压分布为pb，贴近膜片上侧处的声压为pbl；膜片和管道构成a空间，该空间内的声压为pa，贴近膜片下侧处的声压为pau。膜片的面密度为ml，两端的单位长度张紧力为Tl，膜片两侧边界条件为简支。

1.2单腔室鼓型消声器b空间内声压分布

当不考虑z方向时，b空间内的的广义Green函数为[16]

(1)

式中:(x,y)为观察点坐标，(x′,y′)为源点坐标。b空间(m,n)阶特征函数为：

(2)

模态质量

(3)

(4)

由Kirchholff-Helmholtz积分表达式可知，b空间内的声压分布为[17]：

(5)

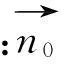
(6)

则腔室侧贴近膜片的声压pbl=pb(x,ha)，利用x方向特征函数的正交性可以得到：

(7)

得到腔室模态辐射阻抗：

(8)

式中：

(9)

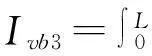
(10)

1.3单腔室鼓型消声器a空间内声压分布

a空间内，无限长管道内的广义Green函数[16]

(11)

(x,y)为观察点坐标，(x′,y′)为源点坐标。管道截面特征函数

(12)

模态质量

(13)

x方向波数

(14)

a空间内声压

(15)

a空间内贴近膜片处的声压

pau=pa(x,ha)

(16)

考虑到

(17)

则利用x方向特征函数的正交性可以得到：

(18)

管道侧模态辐射阻抗表达式为：

(19)

式中:

(20)

1.4单腔室鼓型消声器传递损失求解

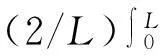
(21)

对于消声器的二维计算，膜片的振动方程简化为一维的弦振动方程：

ml(∂2ηl/∂t2)-Tl(∂2ηl/∂x2)-

(pau+pi-pbl)=0

(22)

考虑到：

(∂2ηl/∂t2)=-jω·v

(23)

(∂2ηl/∂x2)=-(1/jω)·(∂2v/∂x2)

(24)

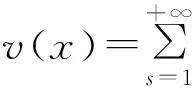
(25)

使用Galerkin方法[2]，在式(22)两边同时乘以(2/L)sin(qπx/L)，并对x在[0,L]上积分，并将式(23)、(24)和(25)代入，得到

(26)

式中：

(27)

(28)

在本文的实际计算中，振动模态和声模态均取至有限项数，例如：s=1,2,3,…,S，m=0,1,2,…,M，n=0,1,2,…,N，下文对此不再特殊说明。求解线性方程组式(26)，即可得到膜片振动的模态振速系数Vs。

求出Vs后，代入a空间声场表达式(15)，考虑到当频率低于管内一阶截止频率时，无穷远处管内高次波已经完全衰减，只取n=0,x=+∞，则传递损失

(29)

式中：

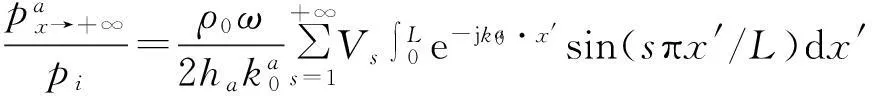
(30)

2双腔并联鼓型消声器分析方法

2.1双腔并联鼓型消声器计算模型

双腔并联鼓型消声器的模型见图2。

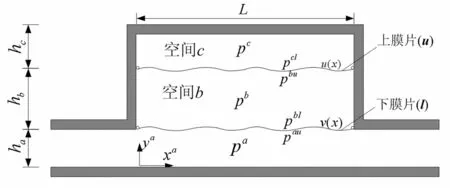
图2　双腔并联鼓型消声器模型 Fig.2 The drumlike silencer with two parallel cavities

管道高度ha，膨胀腔被张紧的下膜片(l)和张紧的上膜片(u)分为两个矩形空间c和b，下部分矩形空间b长度为L，高度为hb，上部分矩形空间c长度为L，高度为hc；上膜片和膨胀腔外壁构成的空间c内的声压分布为pc，贴近上膜片上侧处的声压为pcl；上膜片和下膜片构成的空间b内的声压分布为pb，贴近上膜片下侧处的声压为pbu，贴近下膜片上侧处的声压为pbl；下膜片和管道构成空间a，该空间内的声压为pa，贴近下膜片下侧处的声压为pau。两个膜片的面密度分别为ml和mu，两个膜片两端的单位长度张紧力分别为Tl和Tu。介质声速为c0，密度为ρ0。上、下膜片的振动速度分布分别为u(x)和v(x)。

2.2双腔并联鼓型消声器a、b、c空间内声压分布

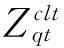
对于双腔并联鼓型消声器的b空间，Green函数Gb(x,y|x′,y′)表达式与单腔室b空间Green函数表达式(1)类似，与单腔室b空间不同的是：双腔并联情况下，b空间内的声压由上膜片辐射声场pb1和下膜片辐射声场pb2共同组成。因此上膜片下侧声压pbu也由两部分组成，即

pbu=pb(x,ha+hb)=

pb1(x,ha+hb)+pb2(x,ha+hb)

(31)

令上膜片振动速度分布为：

(32)

下膜片振动速度分布为：

(33)

与1.2节中的过程类似，利用x方向特征函数的正交性可以得到：

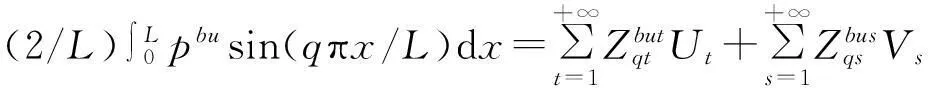
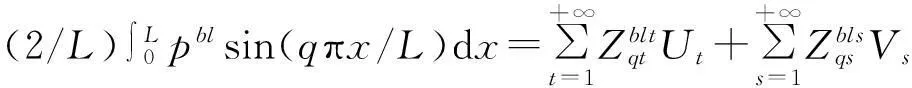
2.3双腔并联鼓型消声器传递损失求解

对入射声波做变换得到入射系数：

(36)

上膜片的振动方程为：

-mujωu-(-Tu/jω)(∂2u/∂x2)-

(pbu-pcl)=0

(37)

使用Galerkin方法，在式(37)两边同时乘以(2/L)sin(qπx/L)，并对x在[0,L]上积分，得到：

(38)

式中：

(39)

下膜片的振动方程为：

-mljωv-(-Tl/jω)(∂2v/∂x2)-

(pau+pi-pbl)=0

(40)

同理，使用Galerkin方法，可以得到

(41)

联立线性方程组(38)和(41)，可以求解得到模态振速Vs和Ut。最后，与式(29)和式(30)表示的过程类似，可以得到双腔并联鼓型消声器的传递损失。

3双腔串联鼓型消声器分析方法

3.1双腔串联鼓型消声器计算模型

双腔串联鼓型消声器的模型见图3。

图3　双腔串联鼓型消声器模型 Fig.3 The drumlike silencer with two in-line cavities

膨胀腔被分为两个矩形空间b和d，左部分矩形空间b长度为L1，高度为hc，右部分矩形空间d长度为L2，高度也为hc；贴近左膜片(1)上侧处的声压为pbl，贴近右膜片(2)上侧处的声压为pdl；贴近左膜片下侧处的声压为pau，贴近右膜片下侧处的声压为pcu，空间a内的声压为p。左右两个膜片的面质量密度分别为m1和m2，左右两个膜片两端的单位长度张紧力分别为T1和T2。介质声速为c0，密度为ρ0。

3.2双腔串联鼓型消声器a、b、c、d空间内声压分布

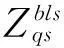
令左膜片的振速分布为：

(42)

令右膜片的振速分布为：

(43)

(44)

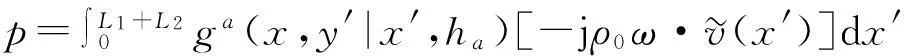
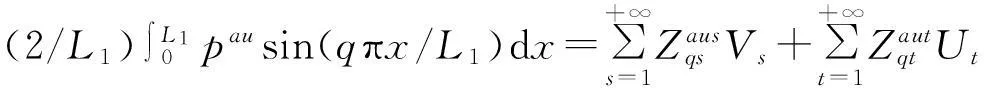
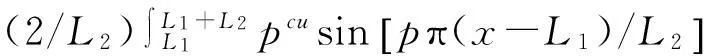
(47)

3.3双腔串联鼓型消声器传递损失求解

对于双腔串联鼓型消声器，对入射声波需要做两次变换以得到入射系数：

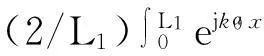
(48)

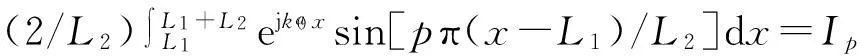
(49)

左膜片的振动方程为：

-m1jωv-(-T1/jω)(∂2v/∂x2)-

(pau+pi-pbl)=0

(50)

使用Galerkin方法，在式(50)两边同时乘以(2/L1)sin(qπx/L1)，对x在[0,L1]上积分，得到：

(51)

同理，对于右膜片，重复(50)和(51)的步骤可以得到：

(52)

联立线性方程组(51)和(52)，可以求解得到模态振速Vs和Ut。与式(29)和式(30)表示的过程类似，可以得到双腔并联鼓型消声器的传递损失。与单腔和双腔并联鼓型消声器不同的是，双腔串联鼓型消声器的下游透射声场的计算需要考虑左右两个膜片共同作用的影响。

4结果及分析

与普通的抗式结构消声器相比，影响鼓型消声器的声学性能的因素更多。为了能在分析问题时减少考虑变量的个数，用三个基本的参量，即ρ0、ha和c0，来对上述推导过程中的各个物理量进行无量纲化处理。这样处理之后，分析鼓型消声器的性能时就能不用考虑介质和相应管道高度的影响，从而得出在不同种介质和不同管道尺寸的情况下的一般性规律。以单腔室鼓型消声器，列出所用的无量纲化过程如下[4]：

x*=x/2ha,y*=y/2ha,hb*=hb/2ha,

f*=2fha/c0,ω*=2ωha/c0,L*=L/2ha,

ml*=ml/haρ0,p*=p/ρ0(c0)2,

(53)

式中，带*的为相应的无量纲量。

当鼓型消声器的外形尺寸确定以后，膜片的面密度和张紧力就决定了其声学性能。膜片的张紧力与膜片的面密度需要精准地配合才能使鼓型消声器的传递损失达到最理想的状态。定义鼓型消声器的传递损失基准值为TLcr，若鼓型消声器在[flow,fup]频率区间上传递损失均大于TLcr，则将[flow,fup]定义为鼓型消声器有效作用频带[4]。鼓型消声器的最优参数组合应当能使fup/flow取得最大值。本文计算中取TLcr=3TLmax，其中TLmax是同样结构尺寸下简单膨胀腔消声器在平面波理论下算得的拱形衰减域的最大消声量。

同时应当注意的是：如果将鼓型消声器中的膜片替换为弹性薄板，则弹性薄板的弯曲刚度将代替鼓型消声器中的膜片张力，从而形成所谓的弹性板消声器[8]。除了结构振动控制方程有所区别外，本文提出的方法可以稍做改动即可运用到二维弹性板消声器的声学性能分析中。对于二维结构，简支弹性板可以简化为简支梁[8]，只需将本文的式(39)和(39)替换为简支梁的相关参数即可。

4.1单腔室鼓型消声器计算结果

基于上述计算方法，使用如式(54)的参数计算了单腔室鼓型消声器的传递损失，并不断优化得到其最优传递损失。本文方法的计算结果与有限元法(FEM)计算结果的对比验证见图4。

hb*=1,L*=5,ml*=2

(54)

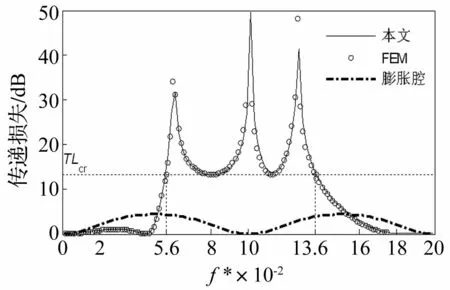
图4　单腔室鼓型消声器的传递损失 Fig.4 The TL of the drumlike silencer with a single cavity

图4中点划线给出的基于平面波理论得到的同样尺寸下的膨胀腔消声器的传递损失。可以看出，对于式(54)的参数组合，单腔室鼓型消声器的最优消声效果主要分布在有效作用频带f*∈[0.056，0.136]上，鼓型消声器在这个区间上的消声效果大大优于同样尺寸的膨胀腔消声器。鼓型消声器的宽频效果主要在于其存在如图4所示的三个传递损失峰值。前述的最优消声效果也是根据这三个峰值确定的，合理选择膜片的张紧力和膜片的面密度，使传递损失曲线上的三个峰值相互靠近并尽量使峰峰间的谷值合理，这样鼓型消声器才能具有宽频范围的大消声量。

4.2双腔并联鼓型消声器计算结果及分析

基于上述计算方法，使用如式(55)参数计算了双腔并联鼓型消声器的传递损失。为了更好地验证本文方法的准确性，令式(55)中的两个腔室的高度不同，两个膜片的参数也不同。计算的结果对比验证见图5。

hb*=0.4,L*=5,ml*=2,Tl*=0.95

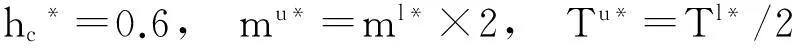
(55)

图5　双腔并联鼓型消声器的传递损失 Fig.5 The TL of the drumlike silencer with two parallel cavities

图5细实线给出的是使用本文上述方法计算得到的传递损失，计算时选取的模态截断数为：S=T=Q=M=25，N=10；○为相应的FEM计算结果。从图5中可以看出，两者计算结果吻合良好，从而验证了本文提出的双腔并联鼓型消声器传递损失计算方法的准确性。

对于鼓型消声器，张紧的膜片和其背后的腔室的共同作用类似于多个亥姆赫兹共振器。研究表明利用多个亥姆霍兹共振器的耦合作用可以拓宽消声频带[18]。

鼓型消声器的声反射性能与膜和腔室的固有频率有关，膜的固有频率与膜的边界条件、面质量、张紧力有关，而腔室的固有频率与腔室的尺寸有关。在简支边界下，膜结构的固有频率与膜的张紧力成正比，与膜的面密度成反比[16]。

从这一点出发，在腔室的尺寸保持不变的前提下，调节双腔并联鼓型消声器中上、下膜的张紧力和面密度的组合，从而使两个膜片的固有频率分离，应当能有助于实现宽带的消声效果。式(55)中的参数组合中，相对于下膜片，上膜片的张紧力小、面密度大，因此上膜片的结构振动的固有频率低于下膜片的固有频率。图6中的粗实线是使用式(55)的参数组合计算出的并联双腔、双膜片对应的传递损失，细实线是单腔室、单膜片对应的传递损失。从图6可以看出，相比于单腔室单膜片，使用具有不同固有频率的并联双模片并不能使有效消声频带拓宽。由于鼓型消声器中的膜片和腔室是完全耦合的，因此，通过简单地调节膜片的固有频率来拓宽双腔并联鼓型消声器传递损失曲线的方法并不恰当。所以，通过改变结构尺寸和膜片参数，重复计算并筛选出最优传递损失，才是双腔并联鼓型消声器最切实有效的优化方法。

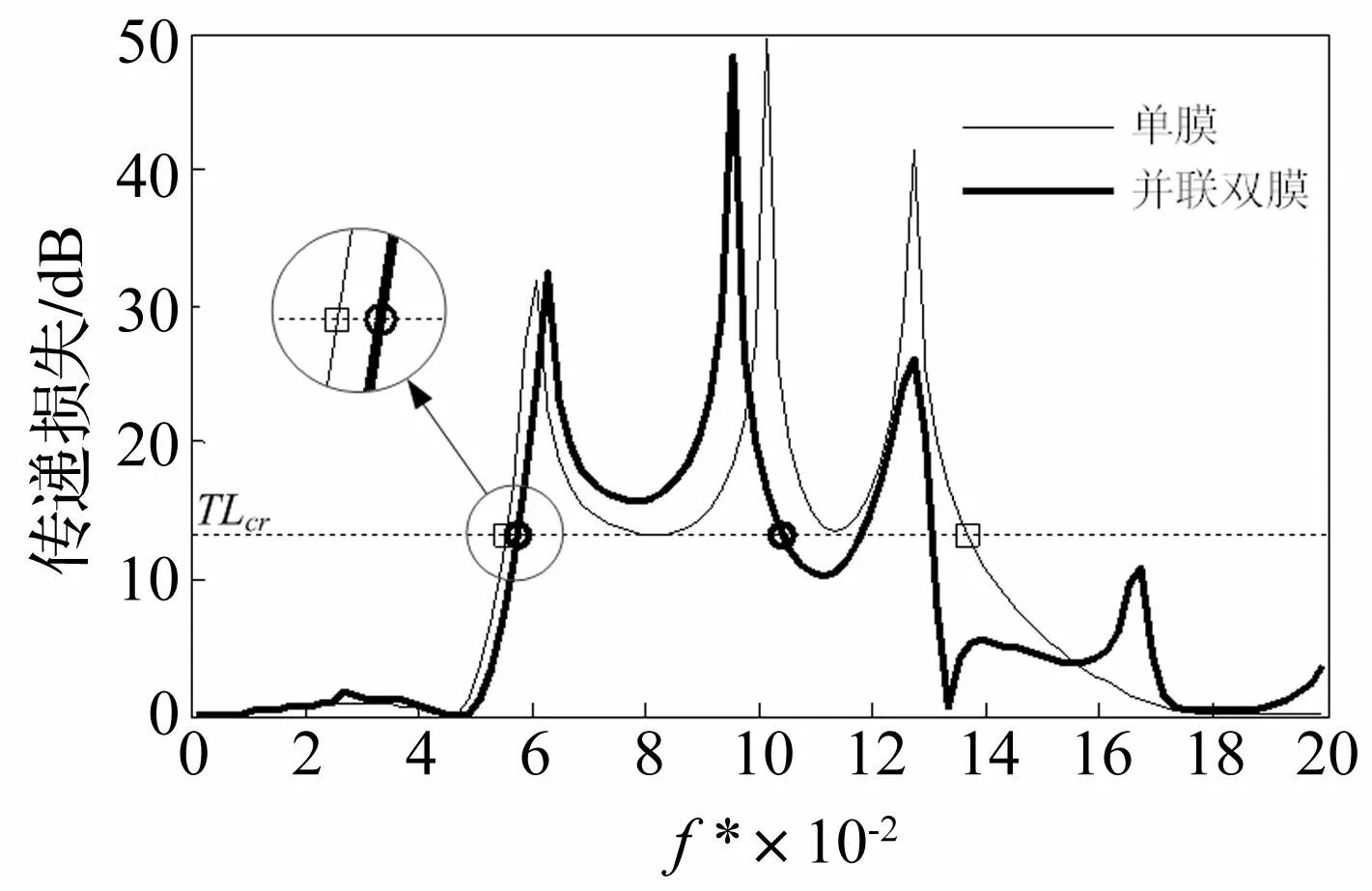
图6　单腔和双腔并联鼓型消声器的传递损失 Fig.6 The TL of the drumlike silencers with a single cavity or two parallel cavities

4.3膜片分布位置对传递损失的影响

膜片在腔室内不同位置时的传递损失，可以用虚拟膜片法得到。所谓虚拟膜片法，就是在双腔并联鼓型消声器计算模型中将下膜片的张紧力和面质量均设置为0，这样就相当于在腔室和管道的连接处存在一个无质量、无刚度的膜，从而保证了腔室和管道求解域交界面上的声压和质点振速连续；而上膜片按实际膜片的参数进行设置。

令膜片距离管道和腔室交界面的偏移量为δ，见图7，则由式(53)可得到无量纲偏移量δ*=δ/2ha。

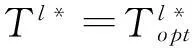
从图8(a)可以看出，当膜片的偏移量较小时，膜片偏移量的增加与背腔的高度减小[19]带来的影响是类似的，均能使传递损失曲线整体降低。

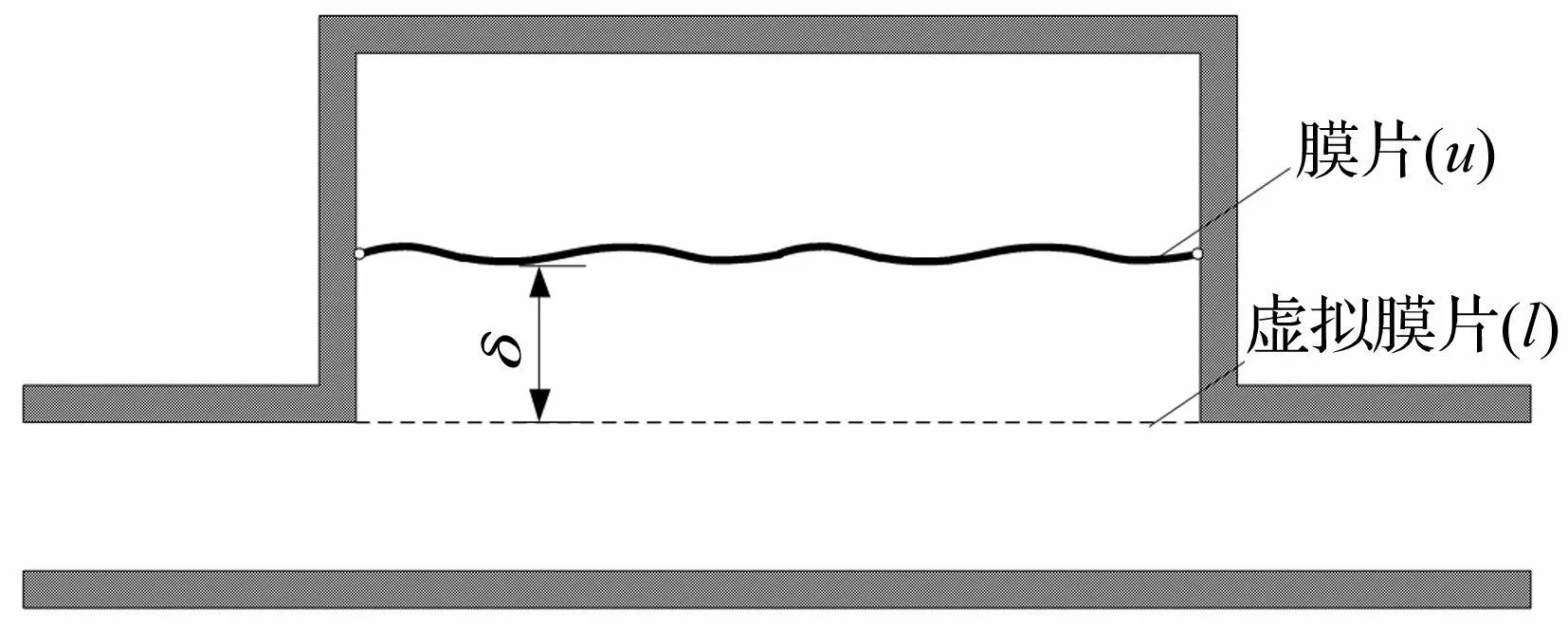
图7　膜片分布位置示意图 Fig.7 Configuration of the membrane position

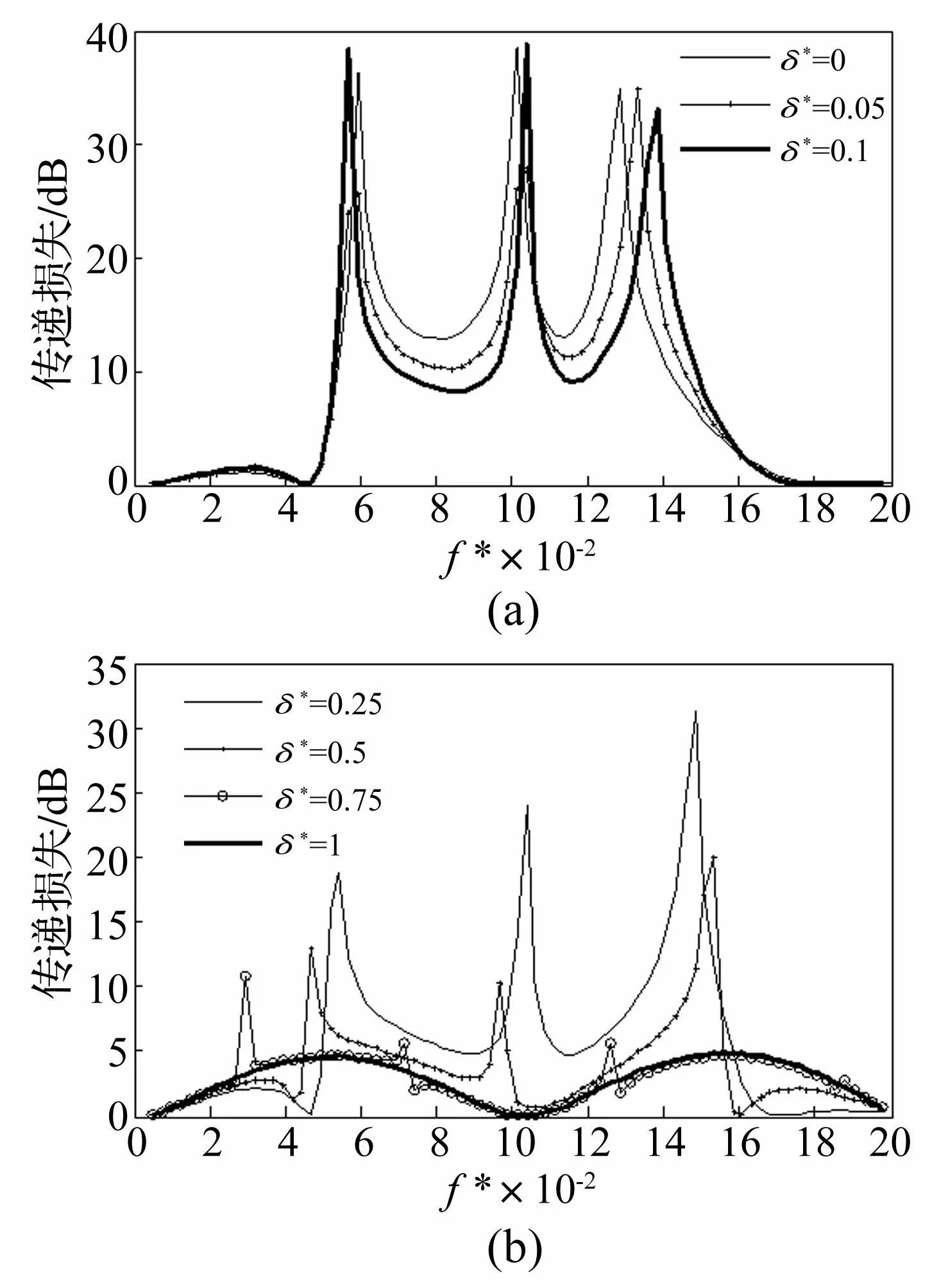
图8　TL随膜片分布位置的变化 Fig.8 The variation of TL versus the membrane position

随着膜片偏移量的进一步增加，膜片外侧背腔内的容积越来越少，背腔侧辐射声刚度逐渐增加，在同样的入射声激励下膜片的振动响应越来弱，其声辐射能力越来越弱，三个相邻的共振峰被削弱和分散，整体传递损失曲线逐渐向膨胀腔的曲线靠近，最终曲线趋近于膨胀腔消声器的拱形衰减曲线，见图8(b)。

4.4双腔串联鼓型消声器计算结果及分析

基于上述计算方法，使用如式(56)的参数计算了双腔串联鼓型消声器的传递损失。计算的结果对比验证见图9，图9表明两种方法计算的结果吻合良好，从而验证了本文提出的计算双腔串联鼓型消声器传递损失的方法的准确性。

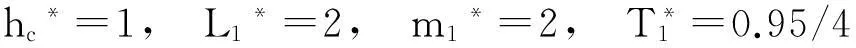
(56)

在消声器的设计中，将多节不同长度的扩张腔串联是错开单个扩张腔通过频率的有效方法。多腔室串联不但能够改善消声器的通过频率，还能提高总的消声量[1]。基于上述原理，本文计算了双腔串联鼓型消声器的传递损失，并和单腔鼓型消声器的效果进行了对比。

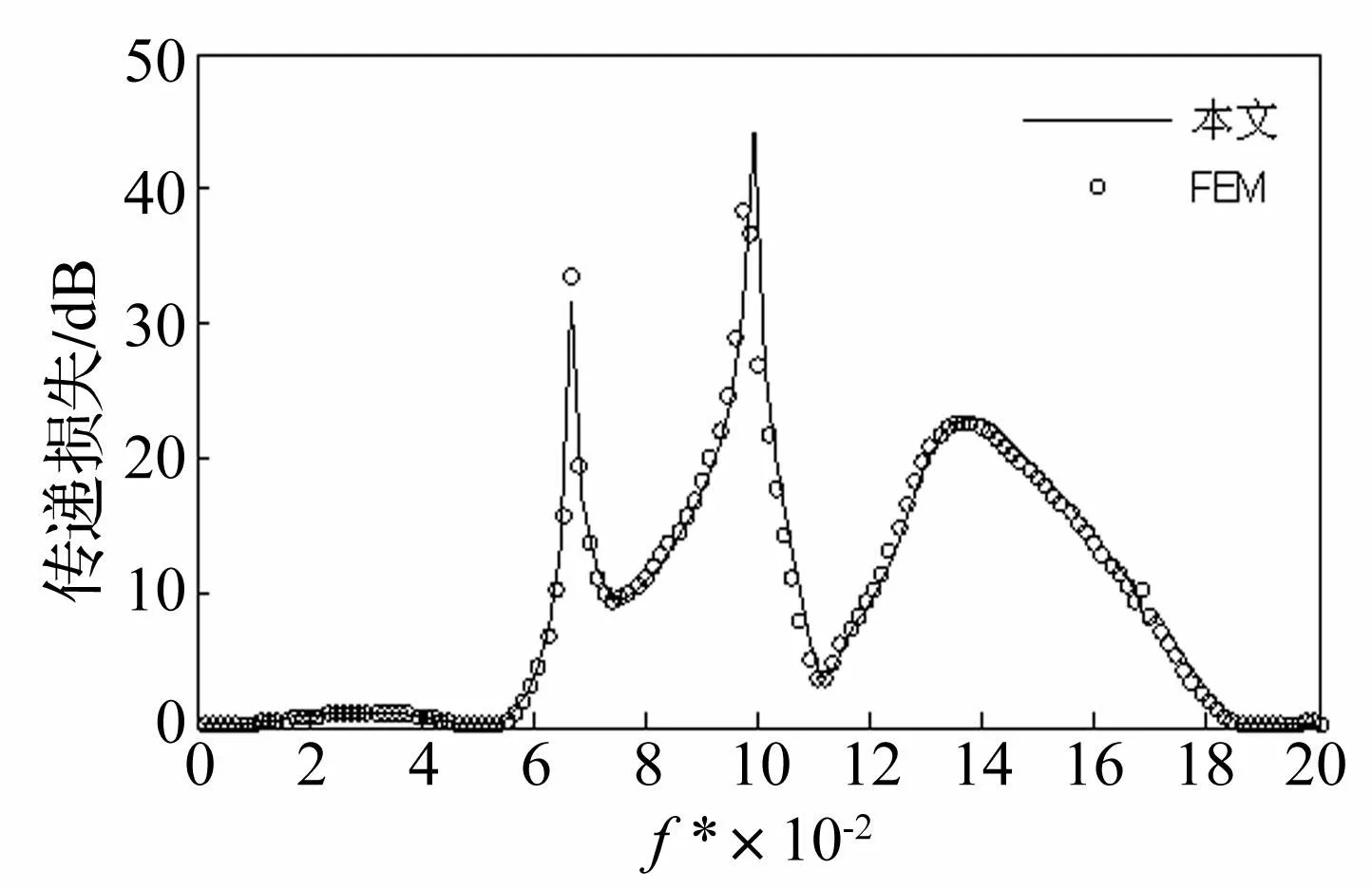
图9　双腔串联鼓型消声器的传递损失 Fig.9 The TL of the drumlike silencer with two in-line cavities

首先对不同膜片长度(腔室长)的单腔鼓型消声器进行了计算和优化。优化参数及消声频带详见表1。

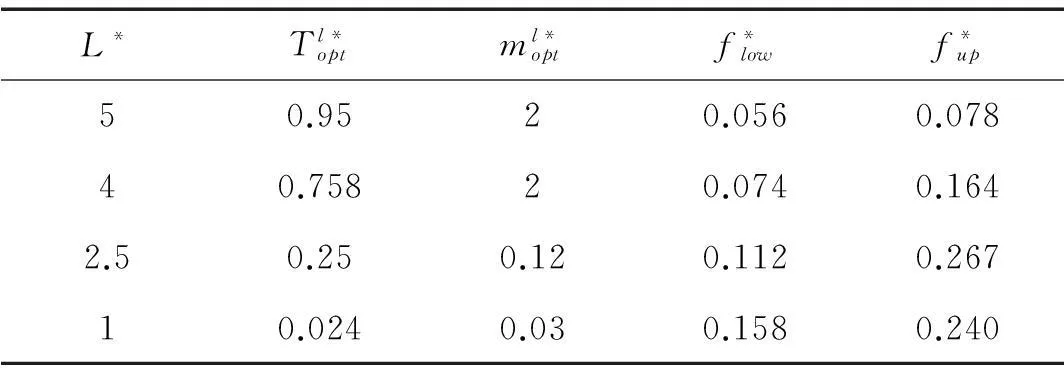
表1　单腔鼓型消声器优化参数及消声频带

注：opt代表优化后的参数

从表1中可以看出，随着膜片长度的减小，膜片所需的优化张紧力和优化面质量均下降，而有效消声频带的下限和上限却向高频移动。这说明使用短膜片(短腔室)将有助于降低鼓型消声器对高张紧力的要求。但同时膜片长度的减少也将使有效作用频带整体向高频移动，不利于消减低频声。鼓型消声器属于抗式消声结构，其膜片长度总是与有效作用频带对应的波长相关，所以若要消减低频噪声，仍然需要使用较长的膜片。

图10对比了将L*=5的单腔鼓型消声器均分为包含两个长度各为L*=2.5短膜的鼓型消声器之后的消声量变化。可见将整体长腔分均分为两个相同、串联的短腔之后，传递损失曲线基本相当于每个短腔单独作用时传递损失曲线的叠加。由于每个L*=2.5短膜的主要消声频率比L*=5长膜的更高，因此分腔之后消声器低频区消声效果变差，而高频区域降噪作用加强，同时有效消声频带变宽，单个膜片所需的优化张紧力也有所下降。

从表1中也可以看出，L*=4对应的有效消声频带的上限与L*=1对应的有效消声频带的下限接近。因此，如果将L*=5的单腔鼓型消声器分为L1*=4和L2*=1两个腔室串联，这两个串联腔室的有效作用频带将会实现互补。图11给出了此种方案下单腔和串联双腔的传递损失对比。

图10　单腔和双腔串联鼓型消声器的传递损失 Fig.10 The TL of the drumlike silencer with a single cavity or two in-line cavities

图11　单腔和双腔串联鼓型消声器的传递损失 Fig.11 The TL of the drumlike silencer with a single cavity or two in-line cavities

从图11中可以看出，长短腔串联搭配的效果基本上是各个独立的腔室作用的叠加，实现了其消声频带的互补；在消声器的外部尺寸保持不变的条件限制下下，相对于单腔室方案，虽然两腔室方案的作用频带下限有所上升，但是却换来了更宽频的消声效果。

5结论

本文使用Green函数和Kirchhoff-Helmholtz积分来计算膜片的辐射声场，从而得到膜片的振动速度，最后计算得到矩形截面管道鼓型消声器的传递损失。并将单腔鼓型消声器的二维数学模型推广到双腔并联和双腔串联鼓型消声器的声学计算中，利用虚拟膜片法研究了膜片在腔室内分布位置的不同对消声器声学性能的影响。本文计算结果与有限元法计算结果吻合良好，从而验证了本文方法计算鼓型消声器消声特性的准确性。

针对鼓型消声器的计算和分析表明：

对于双腔并联鼓型消声器：由于结构振动和声场之间的强烈的耦合作用，通过简单地调节膜片的固有频率并不能达到拓宽消声频带的目的；鉴于目前没有更加直观的方法能计算传递损失峰值与膜片参数的直接关系，因此不断改变结构尺寸和膜片参数进行计算和筛选仍然是最适用的优化方法。

增大膜片和管道的距离，其作用类似于缩减腔室的容积，从而降低了鼓型消声器的传递损失。

单腔鼓型消声器分为两个串联腔室后，将使每个腔室内膜片所需的优化张紧力下降，有利于该类消声器的应用，但是腔室分离之后低频消声效果将变差。

双腔串联鼓型消声器可以通过长短腔室传递损失曲线的互补实现宽频降噪效果。

参考文献

[1]Munjal M L. Acoustics of ducts and mufflers[M]. New York: Wiley, 1987.

[2]Huang L. A theoretical study of duct noise control by flexible panels[J]. The Journal of the Acoustical Society of America, 1999, 106(4): 1801-1809.

[3]Huang L. A theoretical study of passive control of duct noise using panels of varying compliance[J]. The Journal of the Acoustical Society of America, 2001, 109(6): 2805-2814.

[4]Huang L. Modal analysis of a drumlike silencer[J]. The Journal of the Acoustical Society of America, 2002, 112(5): 2014-2025.

[5]Choy Y S, Huang L. Experimental studies of a drumlike silencer[J]. The Journal of the Acoustical Society of America, 2002, 112(5): 2026-2035.

[6]Choy Y S, Huang L. Effect of flow on the drumlike silencer[J]. The Journal of the Acoustical Society of America, 2005, 118(5): 3077-3085.

[7]Chiu Y H, Cheng L, Huang L. Drum-like silencers using magnetic forces in a pressurized cavity[J]. Journal of Sound and Vibration, 2006, 297(3): 895-915.

[8]Huang L. Broadband sound reflection by plates covering side-branch cavities in a duct[J]. J Acoust Soc Am,2006,119(5):2628-2638.

[9]Lawrie J B, Guled I M M. On tuning a reactive silencer by varying the position of an internal membrane[J]. The Journal of the Acoustical Society of America, 2006, 120(2): 780-790.

[10]王晓宇, 孙晓峰. 流管声传播与膜结构相互作用的机理研究[J]. 力学学报, 2006, 38(6): 825-830.

WANG Xiao-yu, SUN Xiao-feng. On the mechanism of the interaction between flexible panels and sound waves in flow duct[J]. Chinese Journal of Theoretical and Applied Mechanics. 2006, 38(6):825-830.

[11]孙晓峰, 王晓宇. 一种新的膜结构消声器理论模型[J]. 北京航空航天大学学报, 2006, 32(10): 1152-1156.

SUN Xiao-feng, WANG Xiao-yu. New theoretical model for drumlike silencer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(10):1152-1156.

[12]Choi S, Kim Y H. Sound-wave propagation in a membrane-duct (L)[J]. The Journal of the Acoustical Society of America, 2002, 112(5): 1749-1752.

[13]Ramamoorthy S, Grosh K, Dodson J M. A theoretical study of structural acoustic silencers for hydraulic systems[J]. the Journal of the Acoustical Society of America, 2002, 111(5): 2097-2108.

[14]Ramamoorthy S, Grosh K, Nawar T G. Structural acoustic silencers—Design and experiment[J]. The Journal of the Acoustical Society of America, 2003, 114(5): 2812.

[15]Huang L, Choy Y S. Vibroacoustics of three-dimensional drum silencer[J]. The Journal of the Acoustical Society of America, 2005, 118(4): 2313-2320.

[16]Morse P M, Ingard K U. Theoretical acoustics[M]. New Jersey: Princeton University Press, 1968.

[17]Fahy F. Foundations of engineering acoustics[M]. London: Academic Press, 2001.

[18]Griffin S, Lane S A, Huybrechts S. Coupled Helmholtz resonators for acoustic attenuation[J]. Journal of Vibration and Acoustics, 2001, 123(1): 11-17.

[19]Huang L. Parametric study of a drum-like silencer[J]. Journal of Sound and Vibration, 2004, 269(3): 467-488.