附加自由阻尼梁高频响应的能量有限元方法模型

第一作者孔祥杰男，博士生，1984年7月生

通信作者陈花玲女，教授，博士生导师，1954年8月生

附加自由阻尼梁高频响应的能量有限元方法模型

孔祥杰1,2， 陈花玲1,2，祝丹晖1,2，张文博1,2

(1.西安交通大学机械工程学院，西安710049； 2.西安交通大学机械结构强度与振动国家重点实验室，西安710049)

摘要：能量有限元方法(EFEA)是一种预示结构高频响应的新方法。为了利用能量有限元方法准确的预示附加阻尼结构的高频响应，将复刚度法与能量有限元的相关理论相结合，同时对现有的能量有限元推导思路进行了大结构阻尼条件下的修正，推导了大阻尼工况下，附加自由阻尼梁结构高频振动响应的能量密度控制方程。同时，通过对阻尼处理交界面处能量转移关系的分析，建立了经过局部附加阻尼处理的梁结构高频响应的能量有限元模型。通过与各自工况下模态解析解的对比，所建立的能量有限元方法模型可以准确的预示大结构阻尼工况下附加阻尼梁的高频响应。

关键词：能量有限元；附加阻尼结构；高频响应预示

基金项目：国家自然科学基金项目(11172222)

收稿日期：2014-05-23修改稿收到日期：2014-08-19

中图分类号:TB123

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.17.016

Abstract:Energy Finite Element Analysis (EFEA) is a method developed for high-frequency structural response prediction in recent years. To study high-frequency vibration responses of beam structures with free-layer damping (FLD) treatment, the governing equation of energy density for bending vibration of beam structures with FLD treatment under large damping condition was derived based on the model of equivalent complex flexural stiffness and the theory of EFEA with special treatments and modifications for high structural damping. Meanwhile, the EFEA model of beam structures with partial FLD treatment was also built by studying the energy transfer relationship at the interface of damping treatment. Numerical simulations verified the proposed model through comparing with the analytical modal solutions. The results showed that the proposed EFEA model can predict the high-frequency vibration responses of beam structures with FLD treatment under high damping condition accurately.

Energy finite element ananlysis for high-frequency vibration of beams with free-layer damping treatment

KONGXiang-jie1,2,CHENHua-ling1,2,ZHUDan-hui1,2,ZHANGWen-bo1,2(1. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China)

Key words:energy finite element analysis; free layer damping (FLD) treatment; high-frequency response

阻尼减振降噪技术是目前常用的振动与噪声控制方法之一，作为其中最常用的一种处理手段，附加阻尼处理对薄壁类大尺寸构件的减振降噪效果特别显著，因此广泛的应用在汽车的外壳、车身立柱，飞机机身舱壁大尺寸薄壁结构的振动与噪声控制中。

在结构共性上，此类大尺寸轻薄的附加阻尼结构的振动响应更多表现为高频响应。目前求解结构高频响应问题的主要预示方法为有限元法、统计能量法和能量有限元方法。

有限元法是目前结构响应分析中使用最广泛的方法。但是，在高频时，为保证运算精度，有限元法所划分单元的个数需要成倍增加，求解时所需的计算时间和计算成本急剧增加，甚至使得求解不切实际而无法实现。同时，高频下结构响应对结构的材料特征微小变化的敏感度远高于低频，因此，有限元法一般用于低频分析，无法完全胜任此类附加阻尼结构的高频响应预示。统计能量法(SEA)是一种较为成熟的高频声振响应的预示方法。它以模态理论为基础，以子系统平均振动响应的能量密度为研究对象，只需用一组线性代数方程便可描述子系统间的响应能量关系，计算效率高。但是，由于统计特征的限制使子系统划分粗大，仅能给出结构粗略的平均响应，无法预测子系统中局部位置的精确响应及响应随位置的空间变化，且不能考虑能量密度在子系统内的变化和阻尼的不均匀性，因此，统计能量法无法满足精确描述附加阻尼结构高频响应的要求。

能量有限元方法(EFEA)是近年来提出的一种高频响应预示的新方法，它基于波动的方法以能量形式描述系统的结构响应，可以描述结构响应随空间变化的情况，结构的几何及阻尼特征可以得到充分表达。能量有限元方法采用有限元数值求解，只需要很少的网格便可以较为准确的预示结果，克服了有限元法在预示高频问题时计算成本高计算时间长的缺点及统计能量法无法预测子系统中局部位置的精确响应及响应随位置的空间变化的不足，是一种非常具有研究价值和发展前景的结构高频响应预示方法。

能量有限元方法由Nefske等[2]提出，他们以梁结构为研究对象，采用能量密度及能量流描述结构的高频响应，最终得到了以能量密度为变量的、近似于热传导方程的二阶微分方程。同时采用有限元对该方程进行离散求解，正式创立了能量有限元方法。随后，Wohlever，Bouthier，Cho等[3-5]先后建立了杆结构、梁、板及耦合结构等基本结构的能量有限元方法模型。在应用研究方面，密歇根大学Vlahopoulos教授研究团队的Zhang、Wang、Lee、Yan等[6-9]先后建立了流体接触结构、复合层合板等结构的能量有限元模型，并应用到舰船、汽车白车身、飞机旋翼等实际结构的高频响应分析中。此外，游进等[10-11]、张文博等[12]、Kong等[13]分别对随机能量有限元、热环境下的能量有限元理论、能量有限元方法的有效性判据等问题进行了研究。

然而，截至目前，有关附加阻尼结构高频振动响应预示的能量有限元模型的相关研究尚未见报道。现有的能量有限元理论在控制方程推导过程中对振动波的波数及群速度进行了小阻尼近似，当结构阻尼较小时，这种基于小阻尼假设的近似引起的误差较小，然而，对于附加阻尼结构而言，为达到相应的减振降噪效果，结构的实际阻尼损耗因子一般很大，若仍采取小阻尼假设而直接使用现有的EFEA控制方程进行求解，势必会带来更大的误差[14]。因此，有必要建立大阻尼条件下的能量有限元模型，对这类结构的高频响应进行精确预示。

本文将复刚度理论与能量有限元相关理论结合起来，以附加阻尼结构中最为常用的附加自由阻尼结构为研究对象，对现有的能量有限元推导思路进行了大结构阻尼工况下的修正，推导了附加自由阻尼梁及局部附加自由阻尼梁高频响应的能量密度控制方程，并采用有限单元法对控制方程进行离散求解。最后，通过与多个工况下的精确模态解析解的对比，证明了本文所建立的能量有限元方法模型可以准确的预示附加阻尼梁结构的高频响应。

1附加自由阻尼梁的能量密度控制方程推导

1.1等效弯曲刚度的求取

图1为附加自由阻尼梁的横截面示意图。在梁整个上表面粘贴了一层附加阻尼层，组成典型的附加自由阻尼结构。其中弹性基层(梁本身)与附加阻尼层的厚度分别为H与H1，梁的宽度为b。图中点划线代表组合梁的中性面位置。

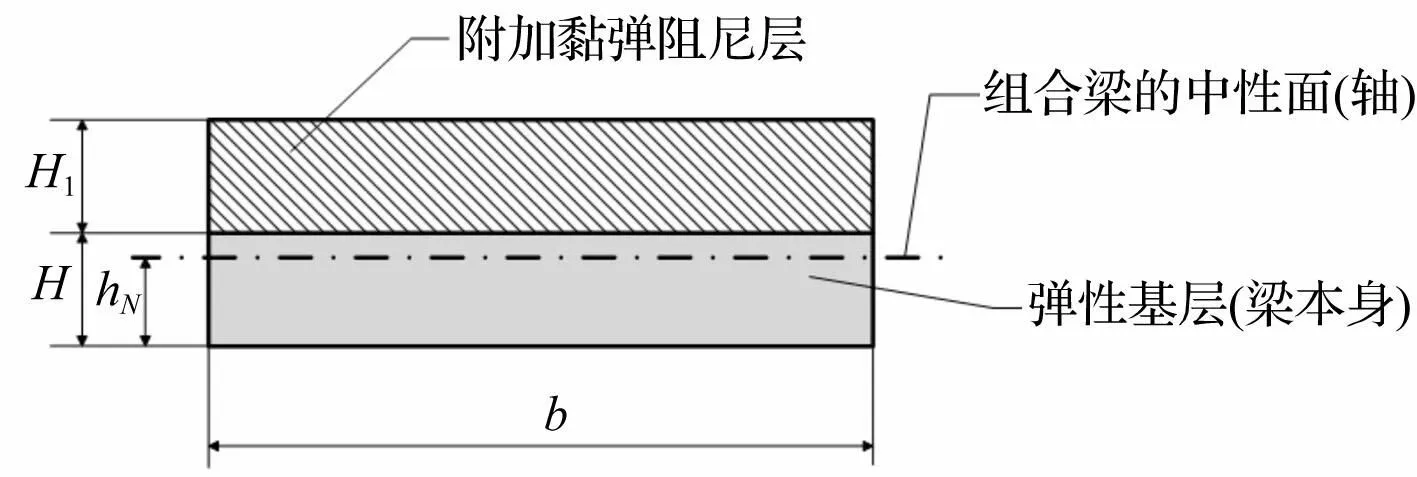
图1　附加自由阻尼梁的横截面示意图 Fig.1 Cross section of FLD beam

(1)

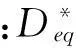
阻尼效应对振动的影响可以用结构阻尼损耗因子η来表述，对附加阻尼层而言，有

(2)

其中：η1为附加阻尼层的结构阻尼损耗因子。

一般而言，梁的弹性基层即梁本身的材质为金属，与附加黏弹阻尼层相比，其阻尼系数要远远小于附加阻尼层，故弹性基层的阻尼系数可以忽略。因此有

E*=E(1+iη)≈E

(3)

式中：η为梁本身的结构阻尼损耗因子。

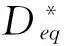
(4)

另一方面，附加自由阻尼梁的等效阻尼损耗因子ηeq可表示为

在求得了等效复弯曲刚度Deq和等效阻尼损耗因子ηeq后，附加自由阻尼梁的横向振动方程便可表示为

(6)

其中：w为梁的横向位移；m为附加自由阻尼梁的总质量，m=ρS+ρ1S1，ρ与ρ1分别为弹性基层及附加黏弹阻尼层的密度，S与S1分别为弹性基层及附加黏弹阻尼层的横截面积；F(x-x0)为作用在x=x0位置上的激励力。

1.2大阻尼条件下能量密度控制方程的推导

忽略掉近场项后，该附加自由阻尼梁的横向振动方程式(6)的位移w的解可表示为

(7)

式中：A与B为由边界条件确定的待定系数；k*为复弯曲波数。

联立式(6)与(7)，可得等效复弯曲波数的表达式为

(8)

其中：定义tanφ=ηeq；ω为振动的圆频率。

对现有传统的能量有限元理论而言，由于一般系统的结构阻尼较小，为了简化推导，对复弯曲波数的表达式(8)进行了小阻尼假设基础上的近似与简化。将指数函数次幂项中的三角函数在小阻尼假设的基础上，进行了等效近似。对传统的能量有限元理论[3]而言，波数可近似表示为

(9)

一般地，定义keq=keq1+jkeq2，则有

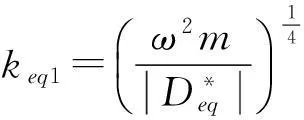
(10)

对小阻尼结构而言，上述近似带来的误差较小[12]。然而，对于附加阻尼结构而言，由于黏弹阻尼层的存在，整个结构的阻尼一般都远大于结构本身的阻尼，当系统的结构阻尼显著增大，对波数进行小阻尼近似带来的误差将显著增加。因此，对附加阻尼结构，为了确保预示精度，更准确的描述系统的响应特性，应该对现有的传统能量有限元理论进行修正，使用未进行小阻尼近似的波数式(8)来进行能量控制方程的推导。

因此，式(8)可以改写为

(11)

则等效群速度Cg-eq可以表示为

(12)

横向振动的附加阻尼梁的能量密度为势能密度和动能密度之和。时间平均的能量密度可以表示为[3]

式中：W为能量密度；“〈〉”表示时间平均；“*”表示共轭运算。

时间平均的能量流可以表示为[3]

(14)

式中：q为能量强度；Re表示取实部运算。

将位移的远场解式(7)及其相应的等效复弯曲波数式(8)代入式(13)和(14)，并在半个波长上进行如下式的本地空间平均，化简后最终可得到

(15)

(16)

联立式(15)和(16)，可得能量密度与能量流的关系为

(17)

定义ηeq-EFEA为附加阻尼结构的等效能量有限元阻尼系数，且

ηeq-EFEA=

(18)

对整个振动系统而言，稳态下的能量平衡方程可以表示为

(19)

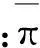
振动系统的能量耗散关系可以近似表示为

(20)

联立能量密度与能量流的关系式(17)、能量平衡方程(19)及能量耗散关系式(20)，可得到附加自由阻尼梁的EFEA能量密度控制方程为

(21)

式(21)即为大阻尼条件下附加自由阻尼梁高频振动的能量密度控制方程。与传统的梁结构的能量密度控制方程[3]相比，式(21)既考虑了附加阻尼层对梁的影响，又采用了完整的波数表达式，无需小阻尼假设，因此能更好的预示附加阻尼结构的高频响应。

采用有限单元法对能量密度控制方程式(21)进行离散求解。离散后的最终的节点单元线性方程则可表示为

[Ke]{We}={Fe}+{Qe}

(22)

式中：上标e为表示该量为单元量；{We}为节点能量密度向量；[Ke] 为单元系数矩阵；{Fe}为外加输入功率矩阵；{Qe}为单元边界节点处内部功率列阵。

2局部附加自由阻尼梁能量模型的建立

上节的推导基于整个梁均进行了自由阻尼处理的情况，在工程实际中，对整个结构均进行附加阻尼处理会大幅提升处理成本。因此，通常仅对弹性基体的某些位置进行局部附加阻尼处理。因此，本节将建立进行了局部附加阻尼处理的梁结构高频响应的能量有限元模型。

图2为一个典型的进行了局部附加自由阻尼处理的梁结构，仅在其中部区域粘贴了黏弹阻尼材料，而其它位置未进行阻尼处理。当振动波传递到附加阻尼层交界面位置时，由于交界面处的刚度、厚度和横截面积等参数发生了改变，振动波将产生部分反射与部分传递的现象。因此，可以将进行了局部附加自由阻尼处理的梁结构等效为数个具有不同物理参数的耦合梁结构的振动问题来处理。

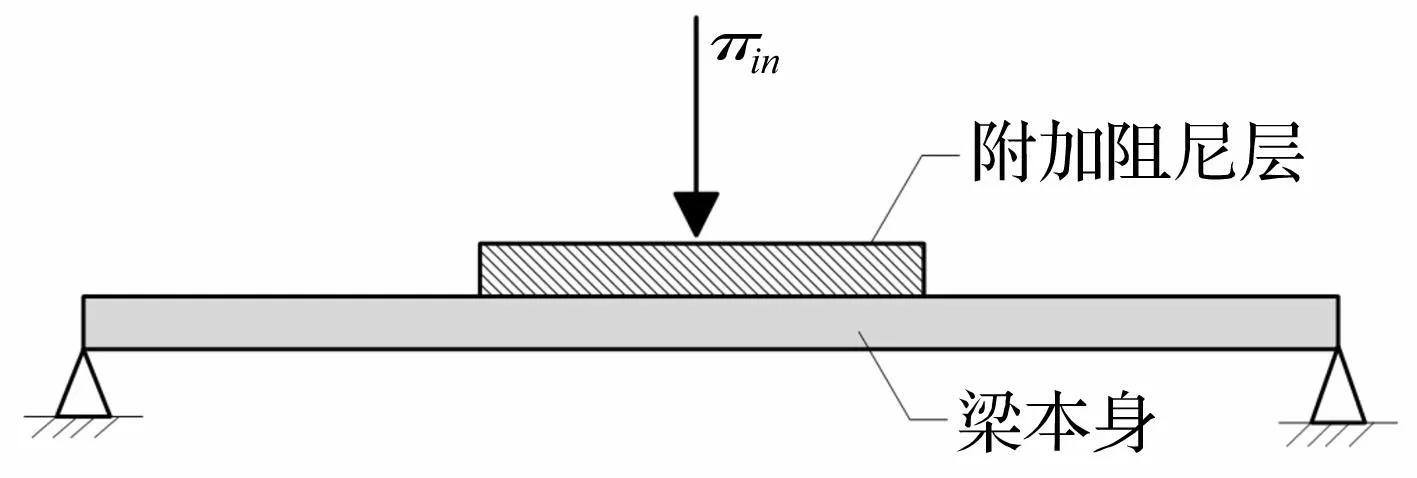
图2　进行了局部附加自由阻尼处理的梁结构示意图 Fig.2 A beam with partial free layer damping treatment

图3为交界面位置的节点示意图，交界面节点位置的能量密度W和能量流q可以用传播出去部分(上标用“t”表示)和反射回来部分(上标用“r”表示)来描述

(23)

qi=qit+qir

(24)

式中：下标i=1表示进行了附加阻尼处理的部分梁，i=2或3表示未进行附加阻尼处理的那部分梁。由于两侧未进行附加处理的那部分梁物理参数相同，故下述推导中用下标2、3或者其中之一(下标2)来统一表示。

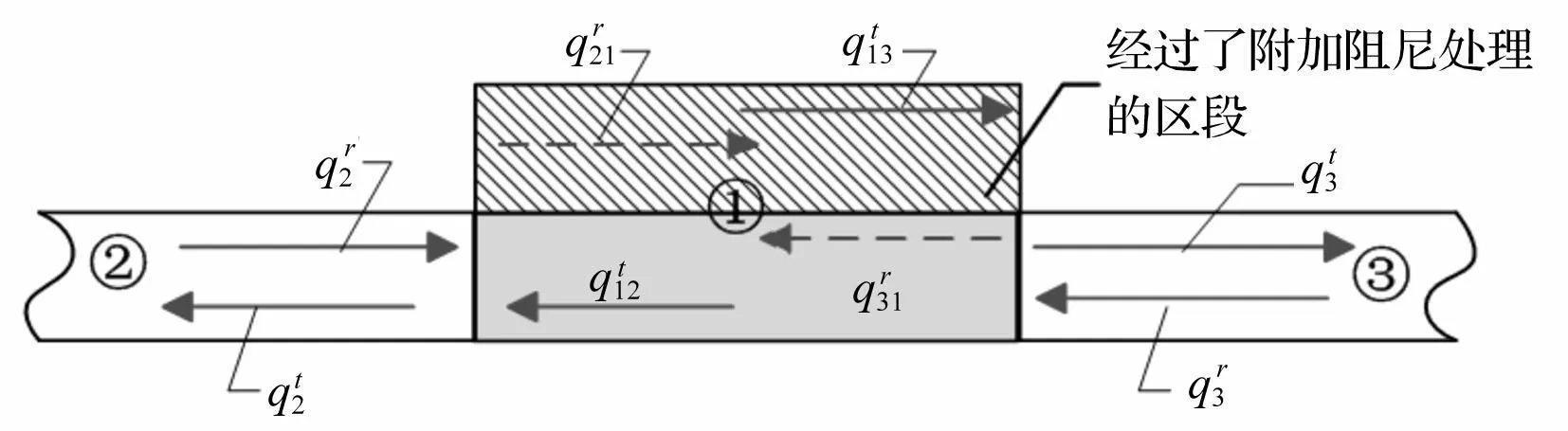
图3　进行了附加阻尼处理和未进行阻尼处理 的交界面位置的节点关系示意图 Fig.3 The interface between the sector with or without partial free layer damping treatment

对于单个正在传递的振动波而言，能量流与能量密度存在如下关系

(25)

如图3所示，流出交界面节点每一侧的净能量可以分别表示为

(26)

(27)

式中：τij为i部分梁到j部分梁之间的能量传递系数；rii为i部分梁的能量反射系数。对于保守耦合的一维梁结构而言，有τij=τji，rii=rjj同时τ+r=1。

将式(25)代入式(26)及(27)可得到

(28)

(29)

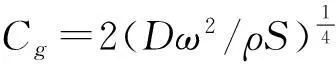
联立式(23)～(29)最终可得到进行了附加阻尼处理和未进行阻尼处理的交界面位置的振动能量转移关系为

(30)

(31)

另外，对于未进行阻尼处理的部分梁的高频响应，可用传统的梁结构弯曲振动的EFEA能量密度控制方程来表示

(32)

参考文献能量传递系数与能量反射系数通过耦合处理交界面位置的位移、剪力弯矩等连续性条件求取，具体方法可[5]。

将进行了附加自由阻尼处理的梁部分的控制方程式(21)及未进行阻尼处理的梁部分的控制方程(32)与阻尼处理的交界面位置的振动能量转移关系式(30)和(32)联立，即可求取局部附加阻尼结构的下高频响应。

3附加自由阻尼梁能量有限元模型的验证

为了验证本文推导的能量控制方程，本节将分别利用一个进行了完全附加自由阻尼处理的简支梁和一个对局部位置进行了附加自由阻尼处理的简支梁进行相关对比验证。EFEA的计算结果将与相应的“精确”模态解析解进行对照验证。为了保证计算结果的收敛性和精度，所有的模态解析解均截取前5000阶模态的计算结果。

3.1附加自由阻尼梁的验证

首先进行完全附加自由阻尼处理的简支梁的能量有限元模型的验证。梁的示意图见图4，简谐激励力作用在梁的中间位置。梁及附加黏弹阻尼层的相关参数如表1所示。

图4　附加自由阻尼梁示意图 Fig.4 A beam with free layer damping treatment

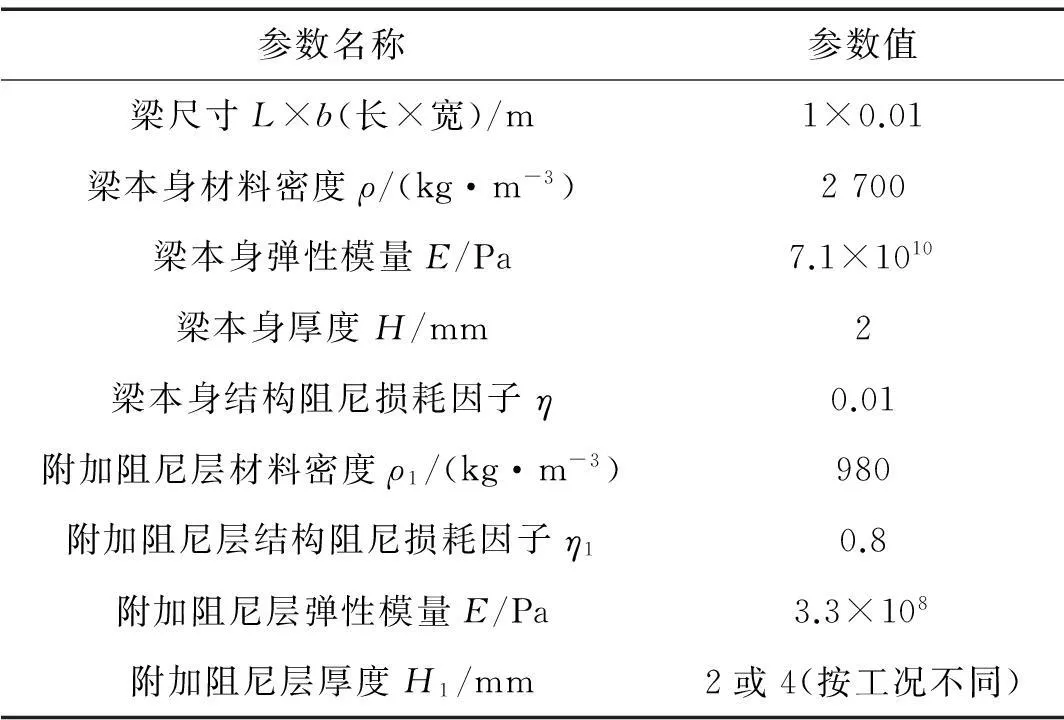
参数名称参数值梁尺寸L×b(长×宽)/m1×0.01梁本身材料密度ρ/(kg·m-3)2700梁本身弹性模量E/Pa7.1×1010梁本身厚度H/mm2梁本身结构阻尼损耗因子η0.01附加阻尼层材料密度ρ1/(kg·m-3)980附加阻尼层结构阻尼损耗因子η10.8附加阻尼层弹性模量E/Pa3.3×108附加阻尼层厚度H1/mm2或4(按工况不同)

需要说明的是，在结构高频响应预示领域，高频的定义是一个相对的概念，并不是一个确定性频率范围，而是一个与结构材料及尺寸参数及激励频率有关的相对概念。一般认为，当分析频率下对应的振动波长远大于结构尺寸时，即可认为该振动频率下的预示问题为高频问题[15-16]。本部分将选取激励频率为2 000 Hz和8 000 Hz两种频率工况进行相关验证，这两种工况下各自对应的振动波波长(0.13 m及0.06 m)均远小于梁的几何长度，属于高频响应问题。

首先计算了激励频率为2 000 Hz，附加阻尼层厚度为4 mm时附加自由阻尼梁沿x方向的振动能量密度，并与模态解析解进行了对比，计算结果见图5。图中能量密度的参考值为10-12J/m(下同)。由图中可以看出，EFEA的预示结果与模态解析解之间有着良好的一致性。EFEA的计算结果较为精确的反映了模态解析解的均值。而在激励点附近，EFEA的预示结果与模态解析解之间存在着一定的误差，其原因是在能量密度控制方程的推导中，忽略了代表渐逝波的近场项。

图5　激励频率为2 000 Hz，附加阻尼层厚度为4 mm时， 沿着x方向上梁的能量密度分布图 Fig.5The energy density distribution along the x-axis across the excitation point when frequency centered on 2 000 Hz with the thickness of damping layer equals 4 mm

图6　激励频率为8 000 Hz，附加阻尼层厚度为4 mm时， 沿着x方向上梁的能量密度分布图 Fig.6The energy density distribution along the x-axis across the excitation point when frequency centered on 8 000 Hz with the thickness of damping layer equals 4 mm

保持其他参数不变，将激励频率增加到8 000 Hz，EFEA与模态解析解的预示结果见图6。可以看到，EFEA的预示结果依然与模态解析解吻合。并且，当激励频率增加后，振动能量的衰减更为明显，与2 000 Hz相比，由激励点到边界位置共0.5 m的长度上，能量衰减量增加了约30 dB，因此，附加自由阻尼对高频振动的减振效果更加的明显。

若附加阻尼层厚度发生了变化，见图7，当附加阻尼层的厚度由4 mm减小到2 mm时，整个梁结构的等效阻尼损耗因子也相应降低，附加阻尼层对振动能量的衰减作用变弱，与4 mm厚度时的预示结果相比，由激励点到边界位置共0.5 m的长度上，能量衰减量降低了将近40 dB。EFEA的预示结果准确的反映了这一现象。

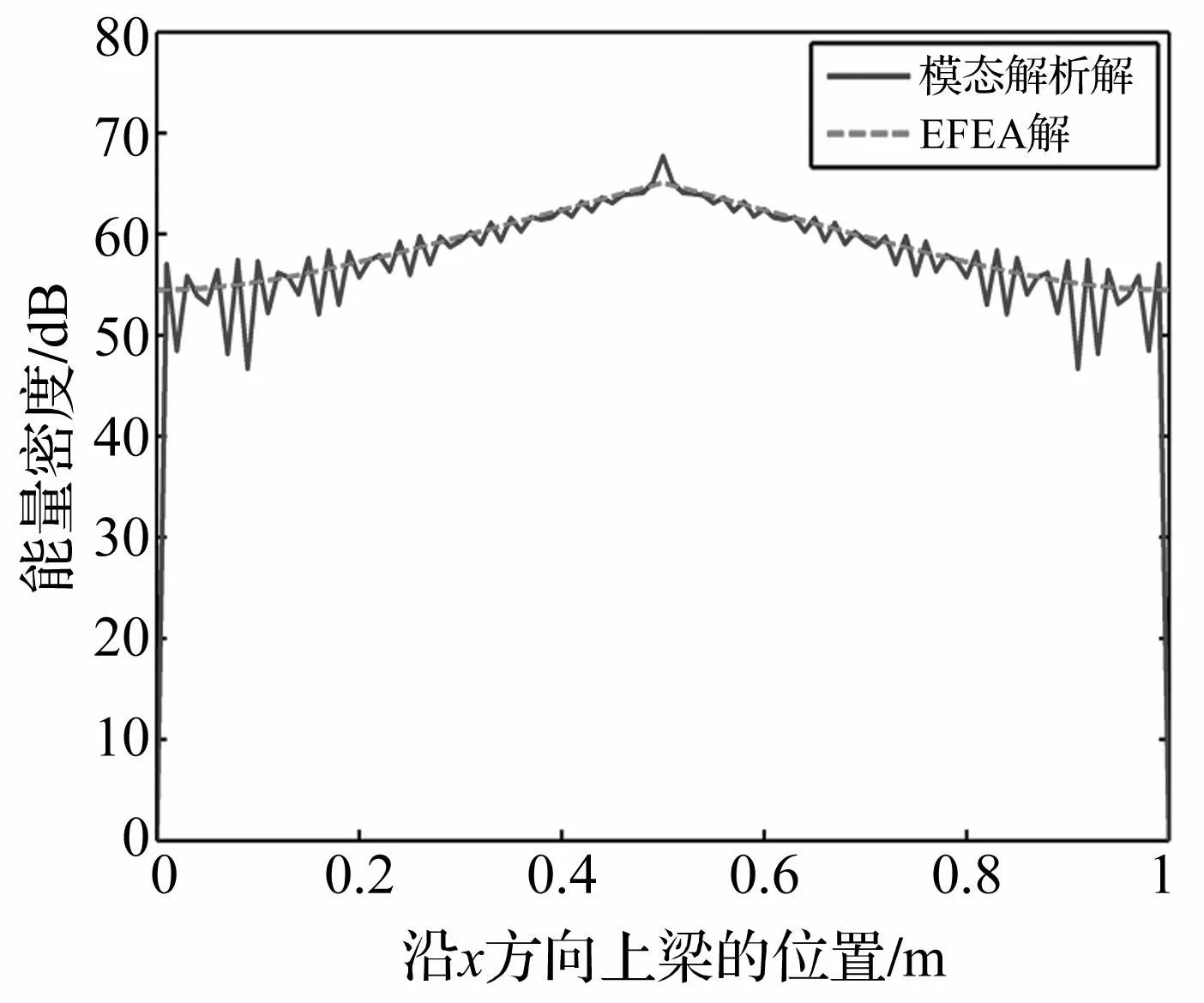
图7　激励频率为8 000 Hz，附加阻尼层厚度为2 mm时， 沿着x方向上梁的能量密度分布图 Fig.7 The energy density distribution along the x-axis across the excitation point when frequency centered on 8 000 Hz with the thickness of damping layer equals 2 mm

图8　激励频率为50 000 Hz，附加阻尼层厚度为2 mm时， 沿着x方向上梁的能量密度分布图 Fig.7The energy density distribution along the x-axis across the excitation point when frequency centered on 50 000 Hz with the thickness of damping layer equals 2 mm

为了验证本章所给出的能量有限元模型在更高的激励频率下对附加自由阻尼梁的预示情况，图8计算了激励频率为50000 Hz、附加阻尼层的厚度为2 mm时，梁结构沿x方向的振动能量密度分布情况。由图5～9可知，当激励频率增加到50 000 Hz后，振动能量更加快速地衰减，而本文所给出的EFEA模型的预示结果依然与模态解析解吻合，可以准确地预示更高频率下的附加自由阻尼梁的响应。

3.2局部附加自由阻尼梁的验证

下面对进行了局部附加自由阻尼处理的简支梁结构进行计算和对比验证。在图2所示的简支梁结构中，梁的中部区域(0.3 m～0.7 m的区段)粘贴了黏弹阻尼层，梁本身及附加黏弹阻尼层的相关参数均如表1所示，其中附加阻尼层厚度为4 mm。

简谐激励力作用在梁的中间位置。激励频率为8 000 Hz。分别采用EFEA的能量密度控制方程和模态解析解对振动能量响应进行计算，结果见图9。

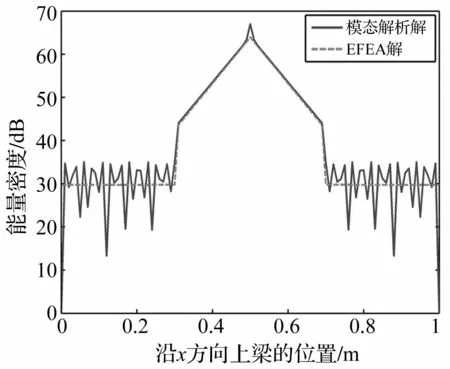
图9　激励频率为8 000 Hz，局部附加自由 阻尼梁沿x方向上能量密度分布图 Fig.9The energy density distribution along the x-axis across the excitation point when frequency centered on 8 000 Hz of the beam with partial FLD treatment

从图中可以看出，对激励点位置进行了附加阻尼处理后，振动能量发生了明显的衰减，结构整体的振动大幅度降低，充分地显示了恰当的局部附加阻尼处理能够带来对高频结构振动的显著减振效果。同样的，EFEA的预示结果较好的反映了进行了附加阻尼处理的区段和未进行附加阻尼处理的区段的“精确”模态解析解的平滑处理后的变化趋势。

通过以上的算例可以看出，本文所给出的能量有限元模型可以较为精确的预示附加自由阻尼结构梁的高频响应。当结构整体的阻尼较大时，预示结果依然具有较高的准确度。

4结论

本文将等效复刚度理与能量有限方法的相关理论相结合，得到了附加自由阻尼梁及局部附加自由阻尼梁高频响应的能量有限元模型。通过与多个工况下的精确模态解析解的对比，对模型进行了验证。对推导出来的控制方程模型讨论如下：

(1)考虑到附加自由阻尼结构的实际结构阻尼较大的实际，在推导的过程中，对现有能量有限元方法的推导思路进行了大阻尼条件下的修正，采用了完整的波数及群速度进行推导，因而可以更准确的预示大阻尼条件下的响应情况，相关验证证明了该点。

(2)对进行了局部附加自由阻尼处理的梁结构而言，本文将其等价为数个具有不同物理参数的耦合梁结构的振动问题来处理，相关验证也证明了这种处理方法是可行的。

[1]Oberst H, Becker G, Frankenfeld K. Über die Dämpfung der Biegeschwingungen dünner Bleche durch fest haftende Beläge II[J]. Acta Acustica United with Acustica,1954,4(1):433-444.

[2]Nefske D, Sung S. Power flow finite element analysis of dynamic systems-Basic theory and application to beams[J]. ASME, Transactions, Journal of Vibration, Acoustics, Stress, and Reliability in Design, 1989, 111: 94-100.

[3]Wohlever J, Bernhard R J. Mechanical energy flow models of rods and beams[J]. Journal of Sound and Vibration, 1992, 153 (1): 1-19.

[4]Bouthier O M, Bernhard R J. Models of space averaged energetics of plates[J]. AIAA Journal,1992,30(3): 616-623.

[5]Cho P E. Energy flow analysis of coupled structures[D]. United States: Purdue University, 1993.

[6]Zhang W G, Wang A M, Vlahopoulos N, et al. High-frequency vibration analysis of thin elastic plates under heavy fluid loading by an energy finite element formulation[J]. Journal of Sound and Vibration, 2003, 263(1): 21-46.

[7]Wang A, Vlahopoulos N, Buehrle R, et al. Energy finite-element analysis of the NASA aluminum test-bed cylinder[J]. The Journal of the Acoustical Society of America, 2006, 119(5): 3389-3389.

[8]Lee S, Vlahopoulos N, Waas A. Analysis of wave propagation in a thin composite cylinder with periodic axial and ring stiffeners using periodic structure theory[J]. Journal of Sound and Vibration,2010,329(16):3304-3318.

[9]Yan X Y. Energy finite element analysis developments for high frequency vibration analysis of composite structures[D]. United States: The University of Michigan, 2008.

[10]游进, 李鸿光, 孟光. 耦合板结构随机能量有限元分析[J]. 振动与冲击, 2009, 28(11): 43-46.

YOU Jin, LI Hong-guang, MENG Guang.Random energy finite element analysis of coupled plate structures[J]. Journal of Vibration and Shock, 2009, 28(11): 43-46.

[11]You J, Li H G, Meng G. Validity investigation of random energy flow analysis for beam structures[J]. Shock and Vibration, 2011, 18(1-2): 269-280.

[12]Zhang W B, Chen H L, Zhu D H, et al. The thermal effects on high-frequency vibration of beams using energy flow analysis[J]. Journal of Sound and Vibration, 2014,333(9):2588-2600.

[13]Kong X J, Chen H L, Zhu D H, et al. Study on the validity region of Energy Finite Element Analysis[J]. Journal of Sound and Vibration, 2014, 333(9):2601-2616.

[14]Cremer L, Heckl M, Petersson B A T. Structure-borne sound: structural vibrations and sound radiation at audio frequencies[M]. Springer, 2005.

[15]Bitsie F. The structural-acoustic energy finite-element method and energy boundary-element method[D]. United States: Purdue University, 1996.

[16]Moens I, Vandepitte D, Sas P. A wavelength criterion for the validity of the Energy Finite Element Method for plates[C]// Proceedings of the International Conference on Noise and Vibration Engineering. KU Leuven; 1998, 2001, 2: 599-606.