千万自由度量级有限元模态分析并行计算研究
第一作者范宣华男,博士,高级工程师,1981年生
千万自由度量级有限元模态分析并行计算研究
范宣华1,肖世富1,陈璞2
(1. 中国工程物理研究院总体工程研究所,四川绵阳621999; 2.北京大学工学院力学与工程科学系,北京100871)
摘要:大规模有限元模态分析在一些重大装备研制过程中有迫切需求,对于实现装置系统级分析具有重要意义。基于隐式重启动Arnoldi、Krylov-Schur和Jacobi-Davidson三种主流算法和PANDA并行计算框架,构建了大规模模态分析并行计算体系;将并行求解体系应用于某光机主体结构,实现了其上千万自由度、数千核的模态分析并行计算;结合算例对三种主流算法的适应性和并行可扩展性进行了评估。研究结果表明,基于三种算法构建的并行求解体系均可在1小时内求解千万自由度量级的大规模模态分析问题,并行可扩展性非常优异。
关键词:有限元法; 大规模模态分析; 并行计算
基金项目:国家自然科学基金面上项目(11472256);中国工程物理研究院发展基金项目(2012A0202008);中国工程物理研究院重点学科项目“计算固体力学”;中国工程物理研究院院长基金项目
收稿日期:2014-05-07修改稿收到日期:2014-08-27
中图分类号:TB123; TP311
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.17.013
Abstract:In the development of large equipments, the demand of large-scale finite element modal analysis is very strong due to its significance in realizing the systemic analysis of the entire large structure. Based on three predominant algorithms, i.e., implicitly restarted Arnoldi method, Krylov-Schur method and Jacobi-Davidson method and PANDA framework, a parallel computing system for a large-scale modal analysis was established. As a typical application, it was used to get solutions to the main structure of a certain optical machinery, a parallel modal analysis with over ten-million-DOF was performed and thousands of CPU processors were applied. The adaptability and parallel scalability of the three algorithms with numerical examples. Results showed that the parallel solving system can perform the modal analysis with over ten million-DOF within one hour and its parallel scalability is excellent.
Parallel computing for finite element modal analysis with over ten-million-DOF
FANXuan-hua1,XIAOShi-Fu1,CHENPu2(1. Institute of Systems Engineering, CAEP, Mianyang 621900, China;2. Department of Mechanics and Engineering Science, College of Engineering, Peking University, Beijing 100871, China)
Key words:finite element method; large-scale modal analysis; parallel computation
在一些特殊大型装备如巨型光机装置、复杂武器系统以及大型飞行器等的研制过程中,往往既需要关注整体动力学特性,也需要关注局部,涉及大规模复杂动力学系统求解,这对传统有限元计算方法和分析工具形成挑战。一方面传统的简化建模会影响结构局部关键细节的预测能力;另一方面大型装备结构复杂,往往包含大量的密集模态,需要精细建模才能得以反映。目前国内现有的商业有限元软件模态分析能力维持在100万自由度量级、数小时的计算水平,无法满足大型装备系统级高精度数值分析的需求。这样以来,高效的大规模有限元计算就显得特别重要。
在动力学有限元分析过程中,模态分析不仅是最耗时间的计算环节,而且也是其他动力分析的基础,其求解精度和效率将直接影响到后续动力分析的可行性和可靠性[1-2]。随着超级计算机的快速发展和大量先进算法的涌现,开展大规模模态分析并行计算的时机也逐渐成熟。本文主要从特征值算法、模态分析并行计算体系构建以及某光机装置大型装备应用等方面介绍我们所取得的一些进展。
1大规模特征值问题求解算法
模态分析在数学上可以归结为大型稀疏矩阵特征值问题,对于该问题的研究大多基于子空间投影技术[3-4]。依据子空间序列产生的方式不同,子空间类方法大致可以分为两类——固定维数子空间法和变化维数子空间法。总体说来变化维数比固定维数的方式更为高效,最具代表性的是Krylov类子空间方法和Davidson类子空间方法,以下分别进行简述。
1.1Krylov类子空间方法
Krylov类子空间方法可以追溯到20世纪50年代提出的用于对称特征值求解的Lanczos算法和用于非对称特征值求解的Arnoldi算法[2, 5],基本思想是通过在Krylov子空间上建立正交基并利用这组正交基将矩阵A缩减成Hessenberg矩阵形式。后来很多学者对基本的Arnoldi/Lanczos算法进行了一系列重启动改进[6-7],比较著名的是Sorensen提出的隐式重启动Arnoldi/Lanczos算法[6],其具体代码实现于ARPACK软件包[7],已经得到广泛应用。Stewart[8]在隐式重启动Arnoldi/Lanczos算法基础上进行了改进,将Arnoldi分解代之以更为宽泛的Krylov分解,提出了更容易代码实现的Krylov-Schur算法。隐式重启动Arnoldi/Lanczos算法和Krylov-Schur算法在数学上具有等价性,是目前Krylov类子空间算法中的两个主流数值算法。
对模态分析而言,其数学本质是求解由质量矩阵M和刚度矩阵K组成的广义特征值方程Kx=λMx,所关心的是低阶特征对。而Krylov类算法多收敛于最大特征值,为此需要进行谱变换。常用的谱变换有Shift-Invert变换和Cayley变换[9]。以Shift-Invert变换为例,对应的变换形式为:

(1)
式中:σ为移位值。通过谱变换可以将原广义特征值问题可以化为标准特征值问题Asx=μsx,其中As=(K-σM)-1M,μs=1/(λ-σ)。在扩展Krylov子空间时,只需要将矩阵A替换成平移-逆处理矩阵As即可,由此带来的问题就是在每个迭代步中都需要求解一个线性方程组,即在增加Krylov子空间序列时,w=Avi变成了w= (K-σM)-1Mvi,要得到w,即相当于求解线性系统(K-σM)w=Mvi。该大型线性方程组的求解是整个特征值算法的关键,一般采用矩阵分解的直接法进行求解,矩阵分解将占据整个特征值问题求解的大部分时间和存储空间。
1.2Davidson类子空间方法
Davidson类子空间方法最初源于由Davidson[10]提出的一种求解对角占优的对称矩阵特征值问题算法,后来逐渐发展成求解一般矩阵特征值问题的广义Davidson算法[1,3,11]。该类算法的一个重大进展是由Sleijpen和Vorst[12]共同提出的Jacobi-Davidson算法。
Jacobi-Davidson方法的核心在于计算“修正方程”,对于广义特征值问题,其修正方程形式为:
(I-MuuT)(K-θM) (I-uuTM)t=-r
(2)
式中:θ为某阶近似特征值(里兹值),u为和θ相对应的近似特征向量(里兹向量),r为留数向量,t为待求的正交补向量。和Krylov类子空间算法的一个重要不同在于,Jacobi-Davidson方法通过得到t的近似解来扩展子空间,而Krylov类子空间方法通过将算子A的幂形式施加到初始迭代向量上来扩展子空间。Jacobi-Davidson方法采用内-外层迭代方式求解特征系统,外层迭代扩展子空间,内层迭代求解“修正方程”。该算法的优势在于计算过程中涉及的运算主要是矩阵-向量积和向量内积,原特征矩阵的稀疏特性得以保留,对内存需求低,并行通讯少;但对不同问题的适应性不如采用Krylov类子空间方法。
2大规模模态分析并行求解体系
围绕隐式重启动Arnoldi、Krylov-Schur和Jacobi-Davidson三种主流算法,我们基于团队研发的PANDA框架[13-14]构建了一套模态分析并行求解体系。Panda框架旨在为大规模并行计算力学应用提供基础支撑服务组件和集成开发环境。该框架基于层次化、模块化及面向对象的设计思路,相应的层次结构见图1。处于底层的基础支撑层形成了Panda框架的核心数据结构,除数学解法器本身的并行机制外,其他并行通讯操作主要在这一部分定义和实现;中间一层为数值共性层,该部分主要提供具有通用性的一些数学计算服务,可根据问题特点和不同需要进行选择使用;最顶层为应用个性层,包含一些单元库、材料模型库及其接口服务等。基于该框架可以为各种有限元计算提供并行分布式数据结构,一方面通过Metis区域分解并行生成有限元计算所需质量和刚度矩阵,另一方面通过集成或研发相应解法器实现大规模有限元并行计算。
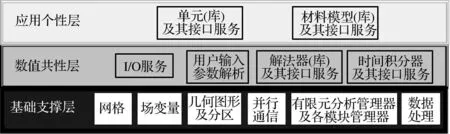
图1 Panda框架的基本结构 Fig.1 The basic configuration of PANDA frame
利用PANDA框架提供的并行数据结构以及接口等功能形成的模态分析求解体系描述见图2。整个体系分成MSC.Patran前处理建模,PANDA框架下的并行计算以及计算结果的后处理三个部分。具体介绍如下:
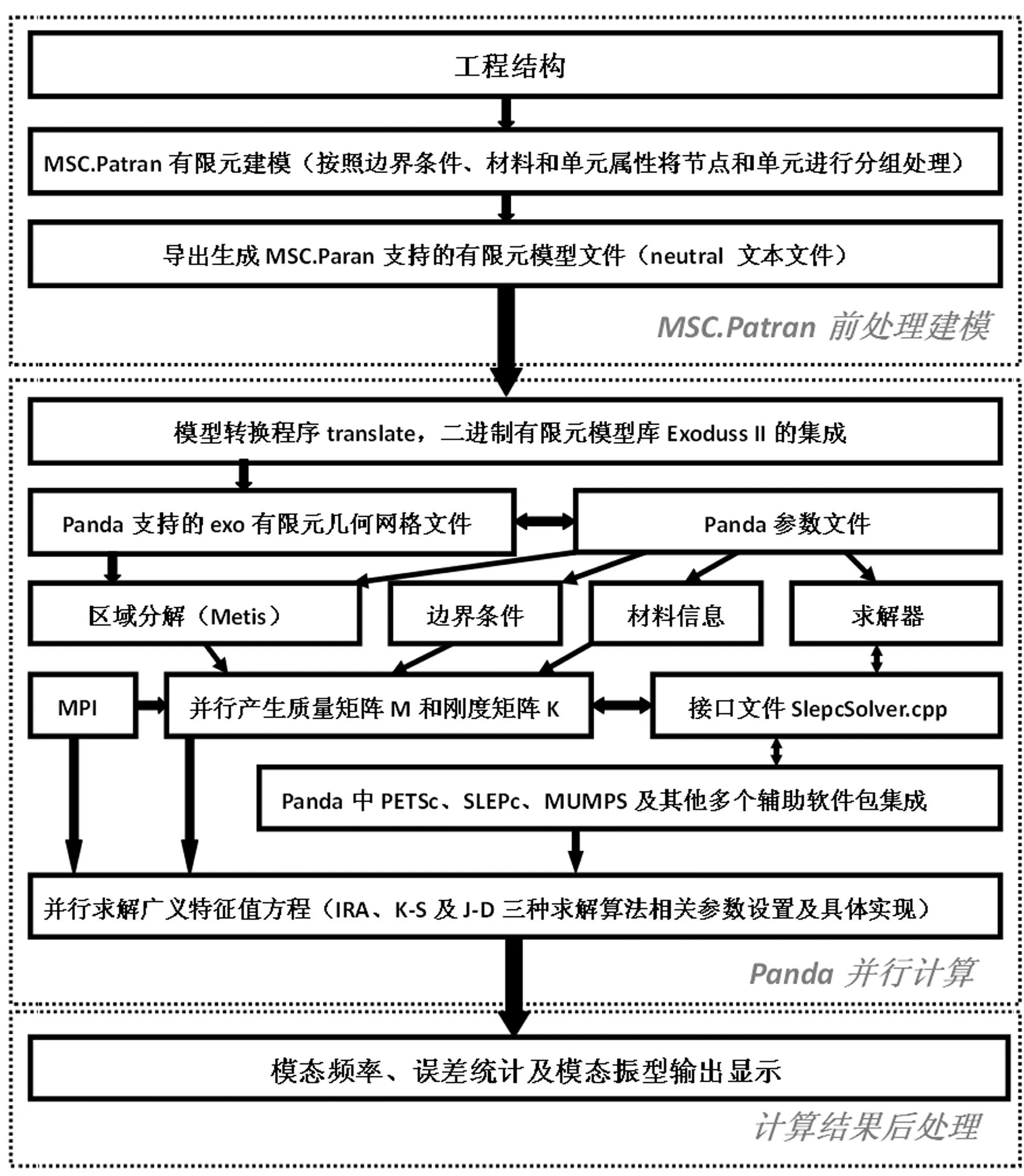
图2 模态分析并行计算体系 Fig.2 Parallel computing system for modal analysis
(1)前处理建模。模态分析的前处理借助MSC.Patran实现。在MSC.Patran中,根据不同单元类型、不同材料和边界约束等对工程结构的有限元模型进行分组处理,然后将这些单元节点信息以MSC.Patran 的中性文件(neutral)形式进行输出,为PANDA并行计算提供基本的有限元模型数据。目前采用MSC.Patran可以在普通工作站上建立千万自由度以上的有限元模型。
(2)PANDA并行计算。该部分是整个模态分析体系的核心,一方面,利用PANDA框架的接口功能将MSC.Patran的网格模型转换成PANDA本身支持的网格模型,通过将美国圣地亚实验室开发的有限元数据库Exodus II接入,实现了模型文本文件到exo格式二进制网格文件的高效转换;另一方面,结合PANDA集成的图剖分软件Metis[15]对有限元网格进行区域分解,利用不同子区域生成质量和刚度矩阵的并行分布式数据结构。生成矩阵后,通过编制的解法器接口调用相应的解法器进行模态分析求解。目前我们在Panda框架下集成了PETSc[16]、SLEPc[17]、ARPACK[7]以及MUMPS[18]等多个数值软件包来实现隐式重启动Arnoldi、Krylov-Schur和Jacobi-Davidson三种主流算法的模态分析并行求解。其中PETSc和MUMPS主要负责矩阵向量的基本运算以及线性方程组的并行求解;SLEPc负责Krylov-Schur算法和Jacobi-Davdison算法的具体实现;APPACK负责隐式重启动Arnoldi算法的具体实现。同时为保证大规模模态分析的收敛性以及计算效率,在各算法和软件中添加了谱变换、内部大型线性方程组求解技术以及内外层优化等关键求解技术,算法详细设计和实现过程可以参见文献[14],限于篇幅在此不过多阐述。
(3)模态分析结果的后处理。主要是模态频率、振型和求解过程中的一些统计信息显示。
3某光机装备典型应用
基于搭建的模态分析并行求解体系,我们开展了大量的工程结构的模态分析计算研究,并对计算软件的正确性与商业软件进行了大量的对比验证,相关工作可参见文献[14]。在此主要给出我国某光机主体结构的模态分析应用。大型光机装置的研制对解决人类未来能源问题及开拓前沿科学技术研究具有重要意义,该装置定位精度和稳定性设计等方面的苛刻要求对大规模数值模拟提出了严峻挑战,数值模拟必须充分反映装置的结构细节响应,由此导致整体结构的有限元计算规模至少要达到数千万自由度以上。
本文所建立的光机主体结构有限元模型见图3,该模型包含了靶球装置、混凝土楼层、钢架等不同结构形式和材料类型,几乎囊括了大部分工程结构类型,图2所示的有限元模型基本能够反映结构本身的复杂特性,此外考虑到脱密等因素,在建模时对装置各部分进行了必要的等效处理,并对各部分材料属性做了相应改变。整个有限元模型采用六面体单元进行划分,约束底部地基部分三个方向自由度。整体结构被划分成百万自由度到千万自由度三种规模,三种情形的相关统计信息见表1。所有规模均求解前50阶模态频率。所有算例的并行测试均在某百万亿次大型集群上进行,该集群包含了数千个计算节点,每个计算节点含两个六核CPU,12个核共享48 GB内存。
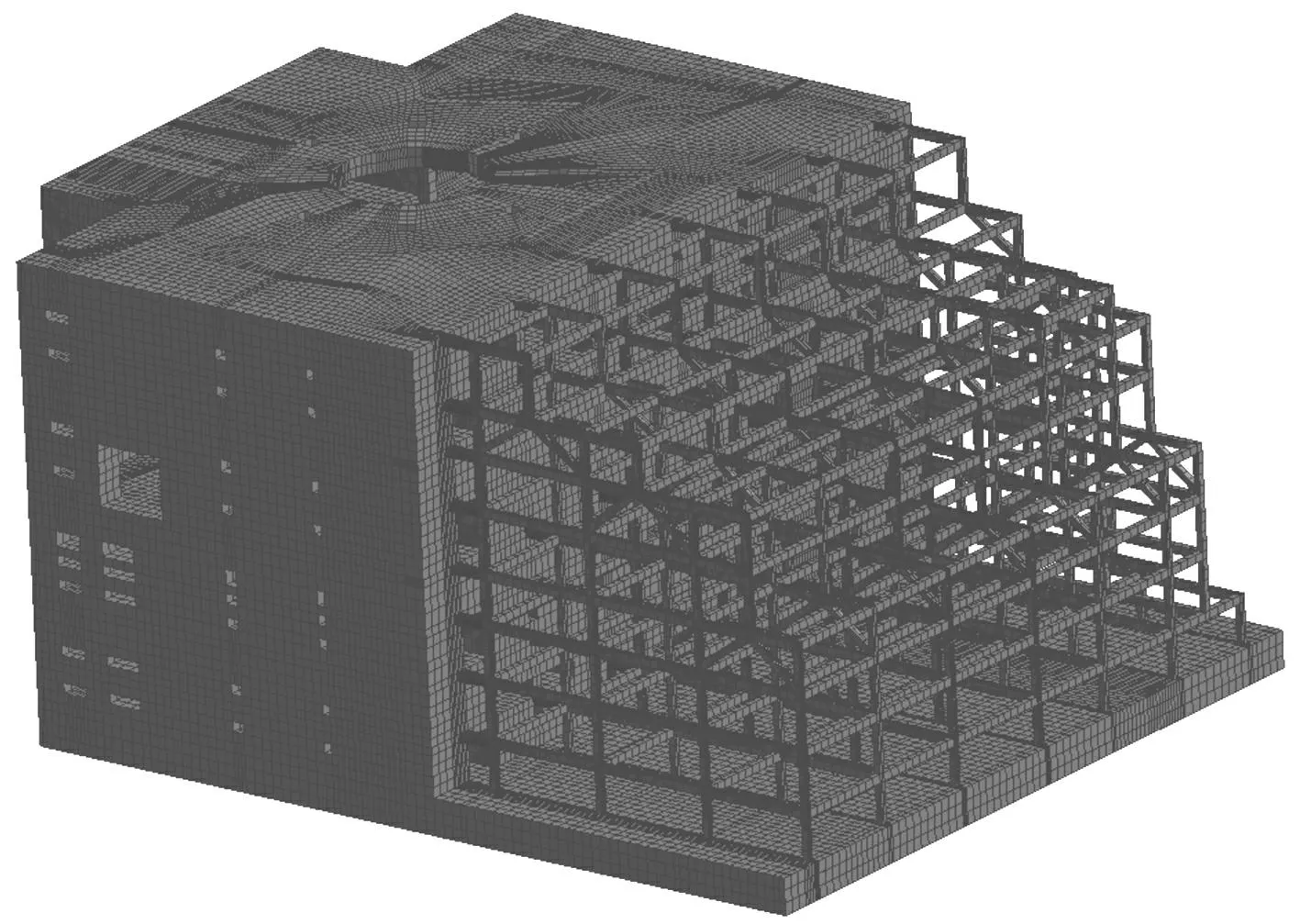
图3 某光机主体结构有限元模型 Fig.3 FEM of Shenguang Structure
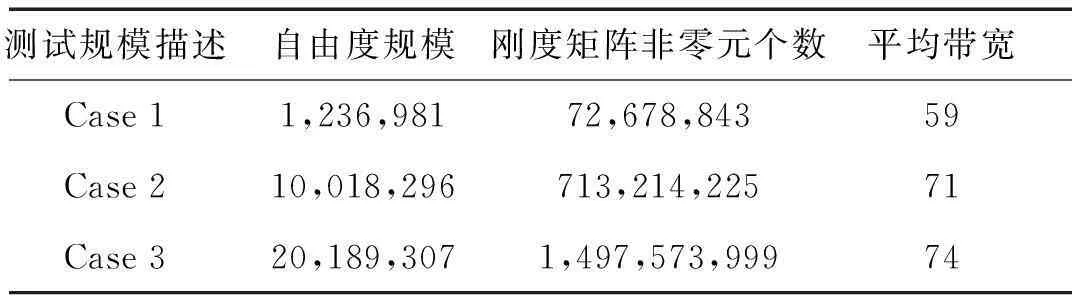
测试规模描述自由度规模刚度矩阵非零元个数平均带宽Case11,236,98172,678,84359Case210,018,296713,214,22571Case320,189,3071,497,573,99974
Case 1的小规模算例主要用来对三种算法的准确性进行验证和比较。首先对三种算法的求解精度采用了留数误差和相对误差双重误差进行评判,这两个误差能够较为充分地反映出各阶频率和振型的求解精度。相应的误差定义如下所示:
εm=‖Kxm-λmMxm‖2(留数误差)
(4)
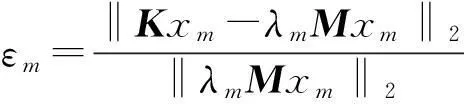
(5)
三种算法求解前50阶模态频率所对应的留数误差和模态误差见图4。
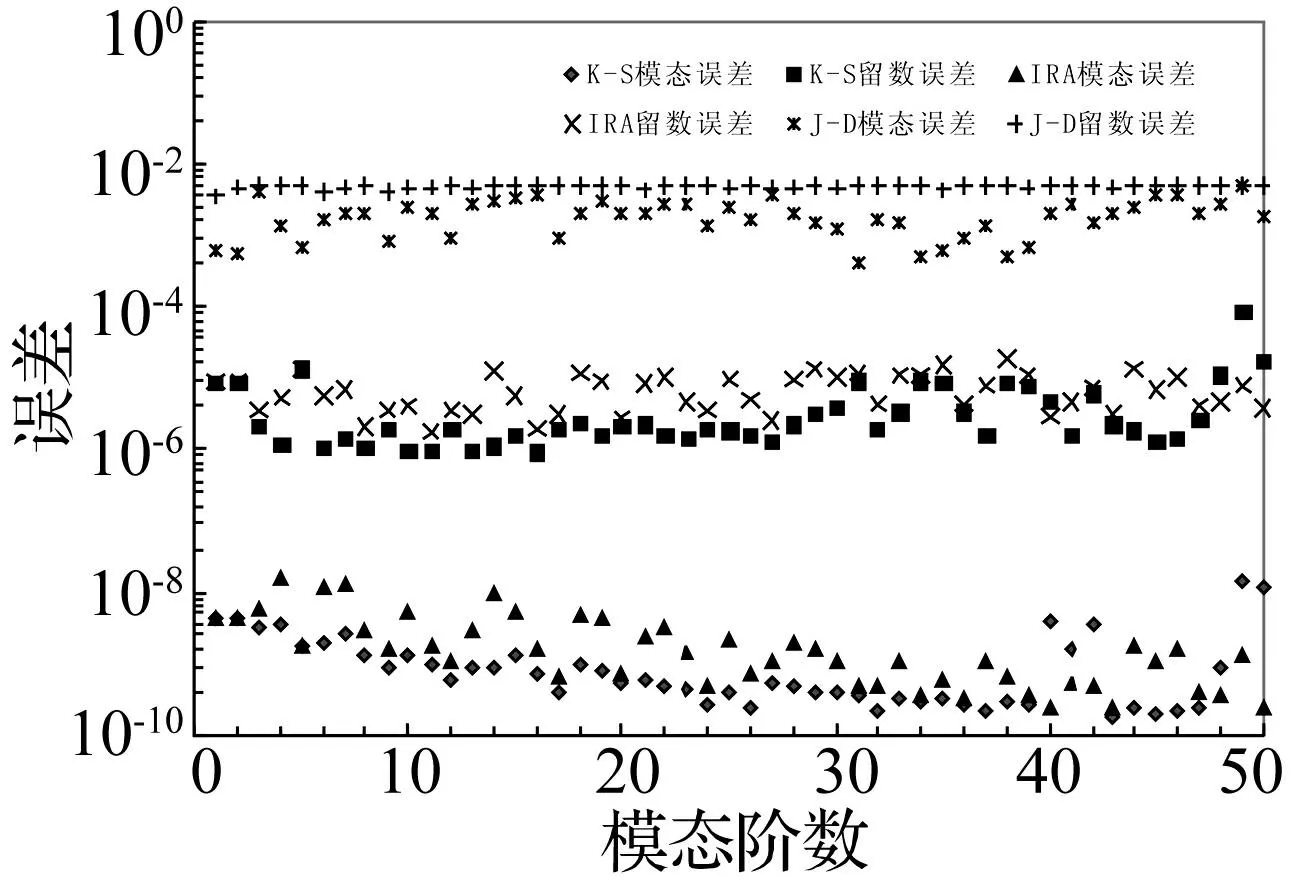
图4 三种算法对应的模态误差和留数误差(Case 1) Fig.4 The modal errors and residue errors for the three methods (Case 1)
从图4中可以看出隐式重启动Arnoldi算法和Krylov-Schur算法各阶频率所对应的留数误差在10-6~10-4之间,模态误差在10-10~10-7之间;而Jacobi-Davidson算法的模态误差和留数误差相对较低,在10-4~10-2之间,这主要是受Jacobi-Davidson算法本身影响,该算法通过内-外层迭代近似求解,为保证内层迭代的收敛性并尽可能减少迭代步数,降低了迭代控制精度。
本文中所采用的三种算法前50阶模态频率计算结果几乎完全一致,三种算法间的相对误差在0.05%以内。此外,还将Case1算例采用相同的单元类型在ANSYS中采用块Lanczos方法进行了对比计算,结果发现模态频率误差也在0.05%以内,各阶振型保持一致。
对于Case2的1000万自由度规模,首先在512个CPU核内对三种算法进行了测试,测试过程发现隐式重启动Arnoldi算法(IRA)和Krylov-Schur算法(K-S)的内存占用大致为400GB,Jacobi-Davidson算法(J-D)的内存占用大致为100GB。三种算法的并行计算时间和效率如表2所示,相应的加速比曲线见图5。
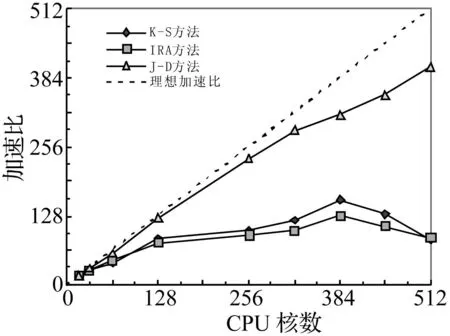
图5 三种算法的加速比曲线(Case 2) Fig.5 The speedup curves for the three algorithms (Case 2)

图6 J-D算法测试得到的加速比曲线 Fig.6 The speedup curves for the J-D algorithms
对于Case3的2 000万自由度模型,隐式重启动Arnoldi算法(IRA)和Krylov-Schur算法(K-S)因矩阵分解失败而无法计算,仅测试了Jacobi-Davidson算法,连同Case2,我们将最大并行CPU核数扩展到了4 800个。表3给出了部分测试结果,相应的加速比曲线见图6。
通过这些测试结果,可以看出以下几点:
(1)对于Krylov-Schur算法和隐式重启动Arnoldi算法(Case2),在400个CPU核附近出现计算了拐点,即随着核数增加,并行计算时间不再降低。这主要是因为两种Krylov类子空间算法在每个子空间迭代过程中都采用直接法求解一个大型线性方程组,矩阵分解带来了较大的内存占用和较多的并行通讯,导致其并行可扩展性相对较弱;而Jacobi-Davidson算法采用内-外层迭代的方式求解特征对,并行通讯相对较少,使得其并行可扩展性非常优异,在512个CPU核内的并行加速比解决理想加速比,且未出现计算拐点。
(2)对于Jacobi-Davidson算法,在Case2的1000万自由度规模时,并行计算拐点出现在2500个CPU核附近;在Case3的2 000万自由度模型时,并行计算拐点出现在3 500个CPU核附近,两种规模的可扩展CPU核数均达到数千个。
(3)综合比较三种算法在各种并行进程下的实际计算时间可以看出,Jacobi-Davidson算法在少量CPU核数的计算时间高出Krylov类两种算法一个数量级以上,随着CPU核数的增加,三种算法的计算时间均缩减在1h内。这主要是在少量CPU核数时,Krylov类子空间算法在线性方程组求解时以存储空间换时间,能快速准确得到扩展子空间向量,体现出一定优势;而Jacobi-Davidson算法的内层迭代使得其获取子空间向量的精度较弱,迭代也相对缓慢,导致整个外层迭代收敛较慢,但随着CPU核数的增加,其优异的并行性能使得计算时间迅速下降,最终和Krylov类子空间算法求解时间相当。
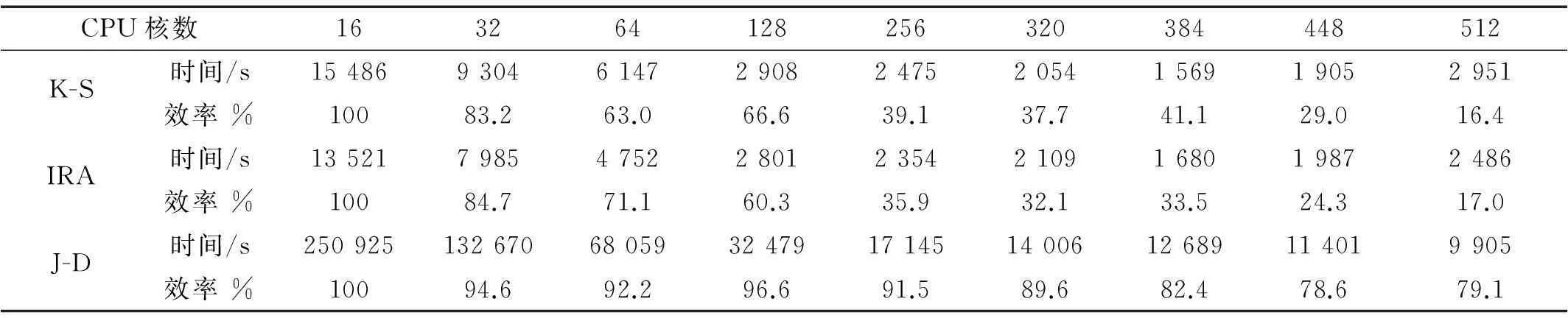
表2 Case 2模型在某大型集群上的计算时间与效率比较

表3 Case 2和Case 3两种规模通过J-D算法测试得到的计算时间和并行效率
此外,为揭示该复杂装置大规模计算的必要性,我们对Case1~Case3的模态频率结果进行了比较分析,表4给出了三种规模前10阶模态频率的对比情况。众所周知,对于工程结构的有限元分析,存在刚度矩阵的“硬化”效应,这会导致在较小自由度规模(有限元网格较稀疏)计算时得到的模态频率偏高,随着网格加密(矩阵规模增大)模态频率会逐渐接近真实频率。我们从Case 1到Case 3的计算结果可以明显发现这一现象,其中其中Case 2的变化率相对于Case 1而言,Case 3的变化率相对于Case 2而言。从表4可以看出,从Case 1的123万自由度规模到Case 2的1000万自由度规模,各阶模态频率发生了比较明显的变化,最大变化率超过10%;而从Case 2的1 000万自由度规模到Case 3的2 000万自由度规模,各阶模态频率的变化率相对低的多。这说明对于光机结构这样的大型复杂结构,百万自由度的计算规模根本无法满足其真实模态频率预测的精度要求,相应的计算规模至少要达到千万自由度以上。

表4 光机结构三种不同规模前10阶
4结论
本文针对大型复杂装备的模态分析问题,通过对三种主流特征值算法进行研究和代码集成开发,在PANDA并行计算框架基础上构建了一套大规模模态分析并行求解体系,该体系覆盖Krylov子空间和Davidson两大类主流算法,并且均具备上千万自由度规模的并行计算能力,基本可以满足大型装备模态分析的需求。
数值算例结果表明,Krylov类子空间算法与Jacobi-Davidson算法具有很好的互补性, Krylov子空间类算法采用直接矩阵分解求解线性方程组,在少量CPU核时会凸显出计算时间上的优势,较快地得到计算结果,但内存占用相对较多,并行可扩展性不如Jacobi-Davidson算法;而Jacobi-Davidson算法采用内-外层迭代方式求解,内存占用比较少,并行可扩展性非常优异,但内层迭代过程会使得少量CPU核时的计算时间远高于Krylov类子空间算法。
参考文献
[1]Saad Y. Numerical methods for large eigenvalue problems[M]. Halsted Press, Div. of John Wiley &Sons, Inc., New York:1992.
[2]尹家聪. 模态分析的自动多重子结构法与动力重分析研究[D].北京:北京大学,2012.
[3]Bai Z, Demmel J, Dongarra J, et al. Templates for the solution of algebraic eigenvalue problems: A practical guide[M]. SIAM, Philadelphia, 2000.
[4]Watkins D S. The matrix eigenvalue problem: GR and krylov subspace methods[M]. SIAM, Philadelphia, 2007.
[5]Arnoldi W E. The principle of minimized iterations in the solution of the matrix eigenvalue problem[J]. Quart. Appl. Math., 1951(9):17-29.
[6]Sorensen D C. Implicit application of polynomial filters in a k-step Arnoldi method[J]. SIAM J. Matrix Anal. Appl., 1992(13):357-385.
[7]Lehoucq R B, Sorensen D C, Yang C. ARPACK Users’ guide: solution of large-scale eigenvalue problems by implicitly restarted arnoldi methods[M]. SIAM, Philadelphia, PA,1998.
[8]Stewart G W. A Krylov-Schur algorithm for large eigenproblems[J]. SIAM J. Matrix Anal. Appl., 2001,23(3): 601-614.
[9]Meerbergen K, Spence A, Roose D. Shift-invert and cayley transforms for detection of rightmost eigenvalues of nonsymmetric matrices[J]. BIT Numerical Mathematics, 1994,3(34): 409-423.
[10]Davidson E R. The iterative calculation of a few of the lowest eigenvalues and corresponding eigenvectors of large real symmetric matrices[J]. J. Comp. Phy., 1975(17): 87-94.
[11]Crouzeix M, Philippe B, Sadkane M. The davidson method[J]. SIAM J. Sci. Comput., 1994(15):62-67.
[12]Sleijpen G L G, van der Vorst H A. A Jacobi-Davidson iteration method for linear eigenvalue problems[J]. SIAM J. Matrix Anal. Appl., 1996, 17(2):401-425.
[13]Shi G M, Wu R, Wang K Y. Discussion about the design for mesh data structure within the parallel framework[C]. 9th World Congress on Computational Mechanics and 4th Asian Pacific Congress on Computational Mechanics, Sydney, Australia, 2010.
[14]范宣华. 基于Panda框架的大规模有限元模态分析并行计算及应用[D].北京:北京大学, 2013.
[15]Karypis G, Kumar V. Metis-a software package for partitioning unstructured graphs, partitioning meshes, and computing fill-reducing orderings of sparse matrices[R]. Technical Report, University of Minnesota, Minneapolis, 1998.
[16]Balay S, Buschelman K, Eijkhout V,et al. PETSc users manual[R]. Technical Report ANL-95/11-Revision 3.0.0, Argonne National Laboratory, 2008.
[17]Hernandez V, Roman J, Tomas A, et al. SLEPc: a scalable and flexible toolkit for the solution of eigenvalue problems[J]. ACM Trans. Math. Softw., 2005, 31(3):351-362.
[18]Amestoy P R, Duff I S, L’Excellent J Y, et al. MUMPS: A general purpose distributed memory sparse solver[J]. Lecture Notes in Computer Science, 2001(1947):121-131.


