节能调度背景下考虑不确定市场信息的机组检修计划



节能调度背景下考虑不确定市场信息的机组检修计划

黄宝鹏

（广东省高级技工学校，广东惠州,516100)

摘要：我国电力工业改革的重要措施之一是实施节能发电调度，交易方式有别于国外实时市场，发电公司检修策略肯定也有所不同。因此，有必要研究节能调度对检修计划制定的影响。检修策略是发电公司中长期生产计划的制订问题，需要考虑中长期负荷和非计划停运等不确定信息。在此背景下，计及负荷和非计划停运等不确定信息，建立机组检修 计划制定策略的随机优化模型，研究节能调度实施后对机组检修计划的影响。算例分析表明了模型的有效性。

关键词：机组检修；节能减排；电力市场；不确定信息；蒙特卡洛法

0　引言

随着我国电力工业市场化改革的逐步推行，电力市场交易形式日趋多样化。针对我国电力工业实际情况，以及全球节能环保要求，我国正试行节能发电调度。目前，很多文献已经研究了节能调度与电力市场的结合，认为其符合电力市场化改革的要求。

传统文献研究了调度机构如何在考虑发电公司申报的检修计划公平调整以满足系统运行需要，文献[1, 2]考虑了现货市场情况下的发电机组检修策略，主要是基于预测市场发电容量充裕度，提出尽量选择在低电价时段检修。我国虽然正在进行电力市场改革，但形式与国外有所区别，包括推行节能调度发电。已有相关文献研究如何将节能调度发电与电力市场结合起来，但尚未见有关节能调度对发电机组检修计划影响的研究。

为研究在电力市场环境下节能调度对发电机组检修计划的影响，本文建立机组检修计划制定策略的随机优化模型，计及负荷和非计划停运等不确定信息，通过研究机组在不同检修计划下的收益情况分析节能调度对发电公司收益的影响。

1　市场环境下的节能发电

节能发电模型是指对燃煤机组煤耗和排放量进行量化，并建立数学模型进行机组负荷的分配。首先， 根据机组煤耗和排放量，计算每台机组的负荷分配因子为

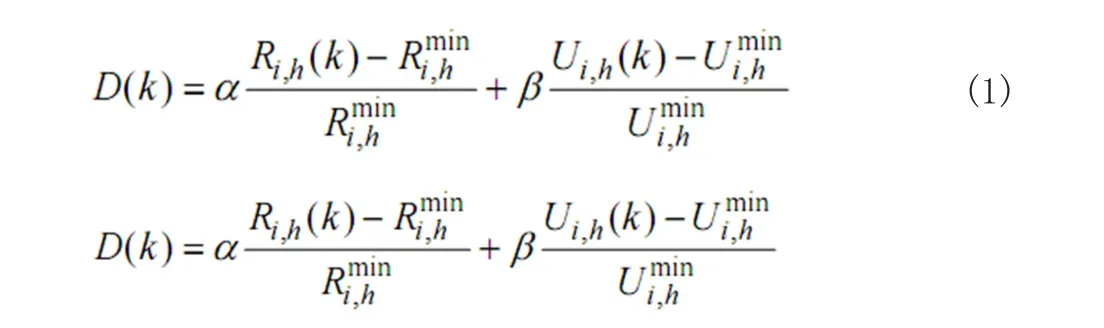
其中，Ri,h(k)为机组k在第i天第h小时的机组煤耗，Rimin,h 为第i天第 h小时所有机组的煤耗中的最小值；U i,h(k)为机组k在第i天第h小时的机组二氧化硫排放量，U imin,h为第i天第h小时所有机组的二氧化硫排放量中的最小值；α和β均为预设的调节系数。由于煤耗在机组运行时间变化不大，且参与节能调度的煤耗数据更改不会过于频繁，因此本文假设 D(k)在机组检修周期内保持不变，忽略其下标 i，h。当机组没有开机时，取 D(k)=0。在发电侧竞价上网后，机组的发电量是由负荷需求和机组发电报价共同决定的。基于煤耗和排放的节 能调度方法是根据机组煤耗和二氧化硫等污染物排放量大小，确定某一负荷惩罚因子，对上网机组的调度电量进行调整或重新分配。假设发电机组的中标容量为 P ′(k)，根据节能调度能耗惩罚模型，其实际出力应为

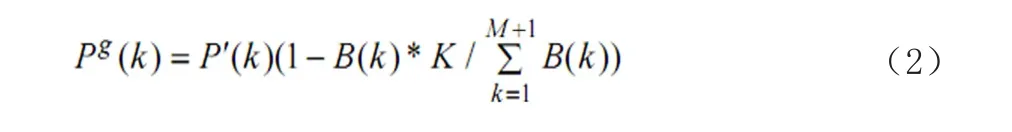
2　市场不确定信息

发电机组检修策略是一个发电公司中长期生产计划安排，需要根据系统的情况制定，因此需要估计机 组自身的运行情况，其他机组的检修计划安排和系统在各时段的负荷大小。

（1）系统可用容量

设系统中共有 M+1 台机组，第 M+1 台机组为所研究发电机组台数。假设系统其他 M 台机组装机容量 一年内不发生变化，系统中所有机组所需检修持续天数均为公共信息。根据历史数据可估计机组 k 的可能

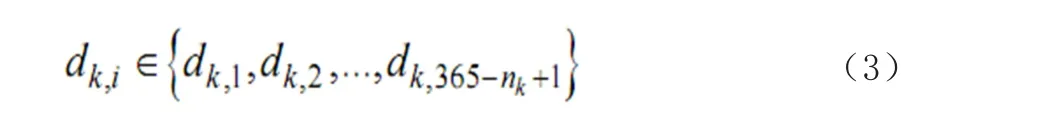
其中， nk为检修持续天数,实际中集合dk,i的元素个数是比较少的。

设某机组的可用容量为其装机容量 Pi,h，记vi∈v1,v2 ,...,v365}表示第i天机组开机状态，例如，机组k在第i天处于开机状态vi(k)1，处于检修状态则vi(k)0。设系统有M+1台机组，则系统总的可用容量为

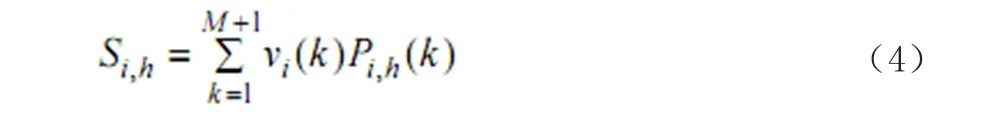
其中，vi(k)为一服从二项分布的随机变量，vi(k)0的概率为φk,i，vi(k)1的概率为1-φk,i。可见，Si,h也为概率性随机变量。此外，vi(k)还要满足连续性约束，即机组一次性连续完成检修工作。即

式中，I表示机组检修起始日在一年中的第I天。例如，机组在1月1日开始检修，则I=1。

（2）负荷调度机构

负荷调度机构或者发电公司都可以根据历史数据和期望增长率等对负荷进行预测。但由于制定检修计划所涉及的时间跨度比较长，年负荷预测属于中长期预测的范畴，面对的不确定性因素多，难以保证准确预测，因此采用概率方法描述未来的负荷在原理上更为合适。假设第i天第h小时的负荷Li,j服从正态分布

式中， Lij 为对第 i 天第 h 小时的负荷预测的期望值，σij 为预测的方差。

（3）电价

定义系统的容量充裕度为γ ( S i,h - Li,j )/Li,j，根据对各国电力市场实际数据的统计和研究，可知系统的容量充裕度与市场电价有关，并且在一定范围内，系统容量充裕度越大，市场电价越低。因此，可采用如下电价与容量充裕度关系式估计实时市场电价为

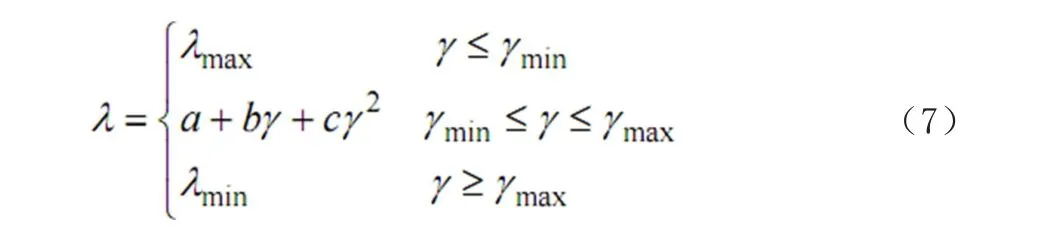
其中γmax和γmin为充裕度曲线的上拐点和下拐点，λmax和λmin为市场电价最高限制和最低限制，a，b，c 为系数。

（4）等效非计划停运率

发电机组存在非计划停运和非计划降出力可能性。一般情况下，机组刚刚启动运行以及长时间运行后，出现非计划停运的可能性较大。记vi′为考虑等效非计划停运的实际运行状态，ξ为非计划停运率。则

由于非计划停运的概率一般很小，即使计及非计划降出力，ξ 的数值也不会太大，也很难统计概率分 布表达式，因此一般使用历史统计数据估算。

3　最优检修策略数学模型

假设机组k在第j月安排检修，λ为结算电价。为示区别，前面所提及的 Pi,h(k)等变量的机组变量均加 了标识“k”，指代某台机组。为了方便，在下面检修策略优化模型的表示中，将选定某台机组作为研究对 象，因此，与机组相关的Pi,h，vi′，ξ 等变量中省略标识“k”。不失一般性，选定第 M+1 台机组作为研究 对象，并假设检修可能起始日为每个月的第一天。记机组的月收益为 fm（m=1, 2,…, 12），由于机组进行检修时，则失去这部分售电收益，因此机组最优的检修计划制定原则应该是，在该检修计划下，机组损失的售电收益 fm 最小。机组月收益的计算方法为

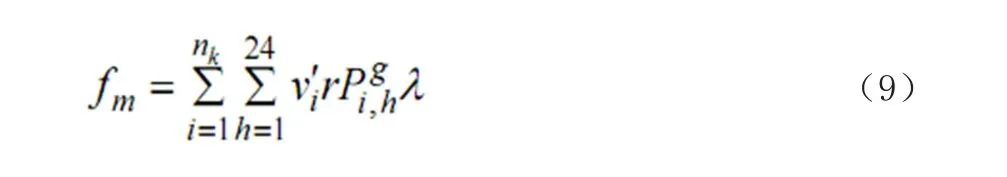
其中，r 为机组被调度发电的概率。 综上所述，结合式（1）到式（9）则可得机组的最优检修策略数学模型为

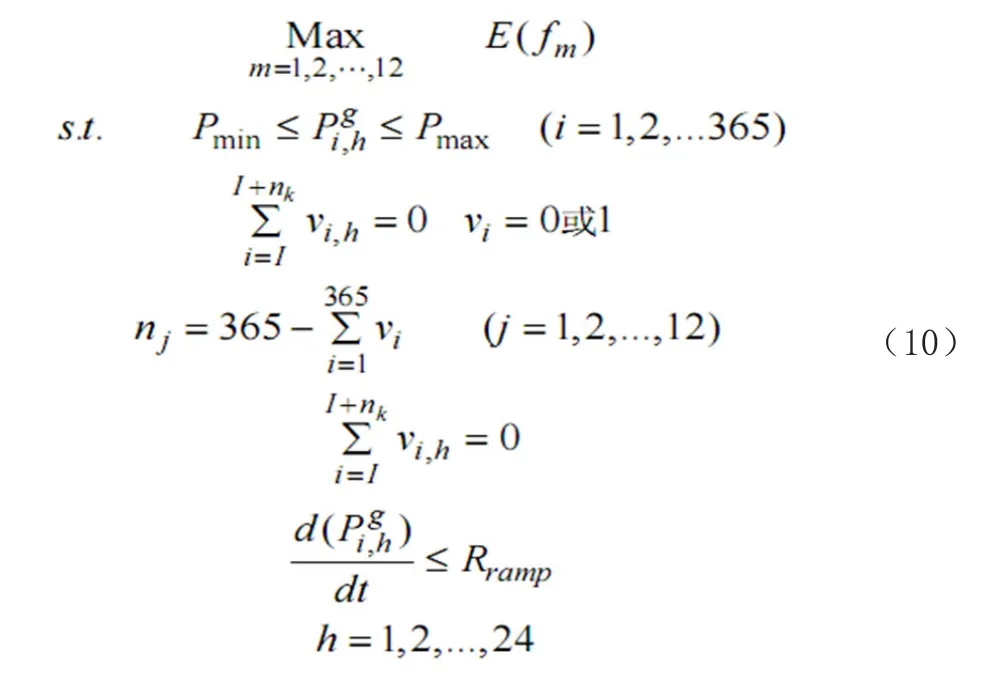
其中， Rramp 为机组最大爬坡能力。

4　算例

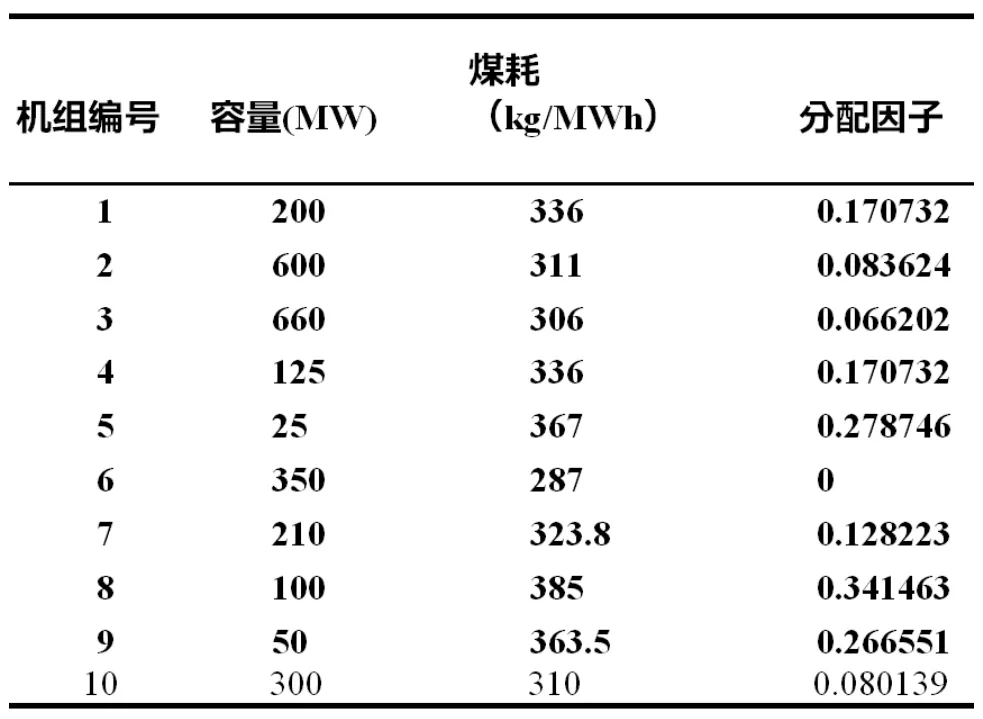
表1　发电机容量和煤耗Table1 capacities and coal consumption of the generating units

设某系统中共有10台机组，即M+1=10,系统中各机组装机容量和煤耗如表1所示。煤耗值采用广东 省实际同容量机组设计煤耗。假设根据各类型的发电机组的计划检修间隔和每台机组上一年度的检修时间，预计发电机组7—10应该在所研究年度进行检修。选取第10台机组为所研究对象，其最小出力限制为150MW，最大出力限制为300MW。发电机组10在所研究年度内计划进行一次检修，检修持续时间为30天。发电机组7—发电机9可能检修起始日期和概率采用文献[1]算例数据，检修持续时间为30天。如表2所示。负荷预测的方法很多，一般可以根据历史负荷数据，以及可能的负荷增长率等对下一年度系统负荷进行预测。为对结果与文献进行比较，负荷数据和机组出力将利用文献[1]的随机方法产生。假定下一年度负荷预测期望值在[1856MW，2080MW]之间，因此在[1856，2080]之间随机产生的 8760 个数据，作为下一年度各时段内发电公司负荷预测的期望值，预测标准差给定为期望值的 3%。机组出力同样用进行随机模拟。 利用在机组的最小出力 Pmin 到最大出力 Pmax 间按均匀分布随机产生一个数值 P ′( k) ，再用式（2）进行调整 后，以 P g ( k) 作为机组出力的期望值，方差为 2% P g ( k) 。假设机组被调度概率 r 在区间[0.5,1]内服从均匀 分布。

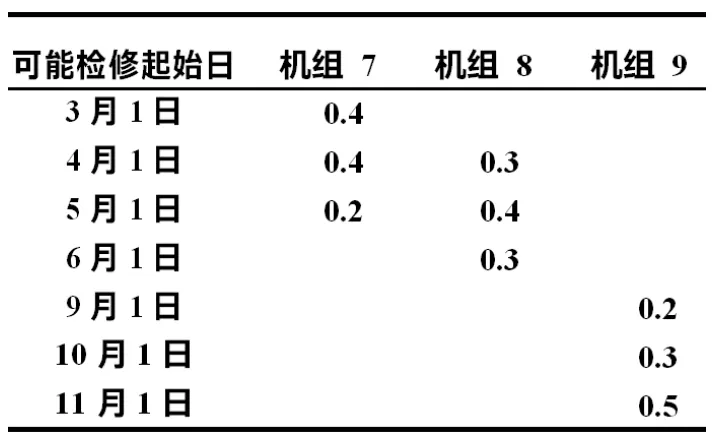
表2　发电机组检修起始日期概率Table2 Probabilities of maintenance starting days of generating units

通常机组运行安全重要性高，非计划停运发生的可能性较小。非计划停运与机组连续运行时间，上次 检修时间，投入时间和使用年限等历史因素有关。一般连续运行时间过长，长时间未检修，设备较旧其非计划停运可能性较高。本文算例假设机组 10非计划停运率在 3%左右。为便于比较，其它参数也根据文献[1]选择如下：

γmax=0.4，γmin=0.05 ；电价上下限λmax=1和λmin=0.1 ，单位为元/kw·h；a=1.28，b=-5.88，c=7.35；计算系数α=0.5，β=0，K=2。利用式（1）到式（9）可以计算不同检修起始日损失收益的期望值如表 3 所示，由于篇幅所限，本文算例只列出每个月第一天作为检修起始日的计算结果。

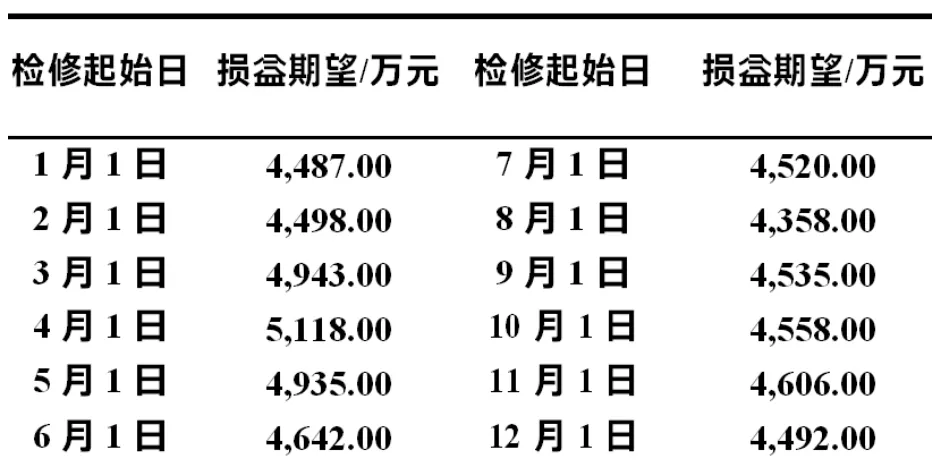
表3　不同检修方案年收入期望值Table3　Expected profit values of different maintenance plans

由表 3 所列的12种情况可知，如果机组10在8月份进行检修，损失的收益期望值最小；如果在4月份进行检修，损失的收益期望值最大。文献[1]得出的最优检修起始日为12月1日，同时，本文算例得由表 3 所列的12种情况可知，如果机组10

在8月份进行检修，损失的收益期望值最小；如果在4月 份进行检修，损失的收益期望值最大。文献[1]得出的最优检修起始日为 12 月 1 日，同时，本文算例得出的各月损益期望相对于文献[1]偏小，原因是节能调度发电中机组10的发电量收到系统机组的煤耗影响， 与实施节能调度前发生了改变。

5　结论

电力体制改革需根据各国电力系统实际，不可以公式化照搬其他国家的模式。根据我国实际国情，我 国正推行和实施节能发电调度，明显有别于国外现货市场环境。在这样的背景下，各独立发电公司和电网 公司有必要研究其对电力企业生产计划和收益的影响。以往对检修策略的研究，均是针对国外现货市场环 境的，有必要进行拓展。本文计及系统容量、负荷和机组非计划停运等不确定信息的同时，综合考虑节能 发电调度，同时，在此基础上建立的检修策略数学优化模型。算例结果表明，节能调度发电将影响机组发 电量，从而影响机组检修计划的安排。

参考文献

[1] 王健,文福拴,杨仁刚.基于发电容量充裕度估计的发电公司检修策略.电力系统自动化.2005.29 (6):45-49.

[2] 王健, 文福拴,杨仁刚. 基于机会约束规划的发电公司最优检修策略.电力系统自动化,2004, 28(19): 27-31.

[3] 傅书逷,王海宁.关于节能减排与电力市场的结合.电力系统自动化, 2008, 32(6): 31-35.

[4] 胡建军,李嘉龙,陈慧坤.基于煤耗和排放的日发电曲线编制模型.电力系统自动化,2009,33(12):43-46.

[5] Antonio J.Conejo.Generation Maintenance Scheduling in Restructured Power Systems. IEEE Trans on Power Systems. 2005, 20(2):984-992.

[6] Deb C.Life-Cycle Maintenance Management of Generating Units in a Competitive Environment. IEEE Trans on Power Systems,2004,19(2):1181-1189.

Maintenance scheduling under energy-saving dispatch considering uncertain market information

Huang Baopeng

（Guangdong Higher Technical School, huizhou city, guangdong province,516100）

Abstract：Trandition studies on generator maintenance scheduling are mainly about its impact on the revenue in arealtime market situation base on MCP.By contrast,energy-saving dispatch is an important measure in China during the restructuring of power industry,therefore it has a different impact on maintenance scheduling.Under this backgroud,the impact of energy-saving on maintenance scheduling is studied,considering the uncertain information such as load level an price.The stochastic model of generator maintenance scheduling with respect to energy-saving dispatch is established,and the Monte Carlo method is applied as the algorithm. Finally,case studies are presented to demonstrate the validity.

Keywords：Generator maintenance;electricity market;energy-saving dispatch;uncertain information;Monte Carlo