基于Choquet积分的绩效评价模型研究 ——以建筑企业为例
基于Choquet积分的绩效评价模型研究
——以建筑企业为例
王文周1施黎蒙1林则夫2
(1.北京师范大学 经济与工商管理学院,北京 100875;2.中央财经大学 管理科学与工程学院,北京 100081)
摘要:针对传统绩效评价模型无法有效的刻画出评价指标相关性的问题,本文引入Choquet积分方法进行企业绩效评价:首先构建考虑指标相关性的企业绩效评价模型,然后基于最大Shapley熵原理计算属性和属性集的重要程度,再运用Choquet积分自下而上计算方案的综合评价值并以此对方案进行排序。实证部分:本文通过10家典型建筑企业的绩效评价进行实证,再将Choquet积分得到的评价结果与常用的TOPSIS方法以及加权平均法进行比较,进一步验证了Choquet积分法方法在企业绩效评价方面的有效性。
关键词:绩效评价;指标相关性;Shapley熵;Choquet积分
收稿日期:*2015-03-10
基金项目:中央高校基本科研业务费专项资金资助(SKZZY2013014)
作者简介:王文周(1975-),男,河南清丰人,北京师范大学经济与工商管理学院讲师,博士,主要从事项目管理和绩效管理研究。
中图分类号:F275;F426.92
文献标识码:A
文章编号:1672-335X(2015)05-0079-07
Abstract:Since the traditional performance evaluation model cannot effectively portray the index correlation, we introduce the Choquet integral to evaluate the performance of construction enterprises. This paper establishes the construction enterprise performance evaluation model taking correlation of the index into consideration. The important degree of attributes and attribute set is employed to calculate the maximum entropy based on Shapley, and then using Choquet integral to evaluate the value of the project and sort them. Finally, the data from 10 typical construction enterprises is used to make an empirical study, comparing the results of Choquet integral and TOPSIS method to validate the effectiveness of the Choquet integral method.
一、引言
企业绩效评价作为一项有效的企业监管制度和管理系统,是企业进行自我监督、自我约束的重要手段。科学合理的绩效评价体系作为一种现代化的管理工具与手段是企业成长发展的持续动力源,它能够帮助企业提高企业效益和内部管理水平,从而提高企业的竞争力水平。
现阶段国外企业的绩效评价主要被分为三个阶段。[1-2]20世纪初,成本绩效评价制度;20世纪20年代—20世纪80年代,企业财务绩效评价体系;20世纪90年代至今,企业创新绩效评价体系。在20世纪80年代前,绩效评价研究的重点是财务评价,着重考虑利润、投资回报率等。
企业绩效评价的方法也随着时间推移和评价目的不同,评价的方法也不同。对于非定量指标大多运用Satty的层次分析法(AHP)和在此基础上演化的模糊层次分析法(Fuzzy AHP),对于非财务指标和财务指标的结合评级则大多数运用数据包络分析(DEA)评价,[3-4]同时DEA中运用最多的模型为CCR模型和BCC模型,[5-7]20世纪末期Robert Kaplan和David Norton提出平衡记分卡法(BSC),随后平衡记分卡法经过完善后得到广泛的使用。[8]同时绩效评价体系除具有代表性平衡积分卡绩效评价体系外还有Medori和Steeple的绩效评价体系和商业流程再造( BPR)绩效评价体系。[9]对于企业绩效指标的研究学者Menches和Hanna通过访谈形式对47个项目经理进行采访并得到了 190个答案,[10]通过对数据定性的分析显示项目经理将项目盈利能力、客户满意度、重复交易、合作关系、安全绩效、沟通管理、进度以及成本作为评价项目绩效的主要指标。英国的环境交通区域部(Department of Environment, Transport, and the Regions, DETR)提出了由成本、工期、质量、客户满意、变更、商业影响以及健康和安全组成的项目绩效指标体系;美国的建筑行业协会(Construction Industry Institute, CII)建立了由工期、成本、变更、安全和返工构成的项目绩效指标体系;英国贸易和工业部(Department of Trade and Industry, DTI)建立了由业主、人以及环境构成的项目绩效指标体系。[11]对于指标权重的确定方法则主要有主成分分析法、熵技术法、灰色关联度法、加权法、TOPSIS法、神经网络法、最优化法等。[12-15]但这些传统的反映绩效评价指标体系相关性的评价方法和模型在具体评价时不能有效区分指标之间积极作用、消极作用等特殊关系,只能通过相关系数(如皮尔森相关系数)来反映指标相关性的大小,辅助决策者设置指标权重,也是一种主观的、间接的相关性度量方法。
由于企业绩效评价因素的不确定性以及诸因素之间关联的复杂性传统的技术方法难以提供有效的解决方案。所以本文针对传统绩效评价模型无法有效的刻画出评价指标相关性的问题,充分借鉴现有成果,[16]建立了基于Choquet积分的绩效评价模型方法:首先分析综合绩效评价体系中指标的关系,然后基于最大Shapley熵原理计算属性和属性集的重要程度,再运用Choquet积分自下而上计算方案的综合评价值。最后基于10家典型建筑企业的绩效评价进行模型实证。
二、方法与原理
(一)企业绩效评价指标相关性机理分析
在各种各样的评价过程中,由于系统之间的相互联系和相互作用,评价指标之间或多或少存在着某些相关关系。在绩效评价时,如果忽略了指标之间的相关性,往往会导致评价与实际情况不相符,可能会过高或过低评价企业的绩效。本文将建筑企业绩效评价指标体系之间的关系分为三种:互补或者积极作用、冗余或者消极作用、独立性。前两种属于相关关系,后一种情况说明指标之间独立,没有相关关系。
1、互补或者积极作用
两个属性联合在一起,重要性不小于这两组属性单独使用时的重要性之和,即将两组属性组合在一起对总体绩效的贡献相对于两组属性单独使用的贡献之和会有提高。
2、冗余或者消极作用
两个属性联合在一起,重要性不大于这两组属性单独使用时的重要性之和,即将两组属性组合在一起对总体绩效的贡献相对于两组属性单独使用的贡献之和没有提高。
3、独立性
两个属性联合在一起,重要性等于这两组属性单独使用时的重要性之和,说两组属性之间不存在交互作用和影响。
(二)Shapley熵
Shapley值是表征参与者在合作中贡献重要性的指标,Shapley熵则是基于概率测度的信息不确定性函数。它被广泛用于解决经济领域中的评估与决策问题。
定义1(Shapley熵):设X={xi,x2,…,xn}为有限集合,[17]P(X)是X的幂集,令L为P(X)上的模糊测度,Shapley熵H是关于L的不确定性测度:
(1-1)

(三)模糊测度和模糊积分
模糊测度和模糊积分作为经典测度和积分的延伸和拓展,重点研究了一种非可加情况。[18]由于可加性是一种理想状态,大多数复杂的实际问题都是非可加的情况,故使用模糊测度和模糊积分作为数学模型会比使用经典的测度和积分更符合实际情况,因此模糊测度和模糊积分作为描述非可加和非线性的数学模型有着许多应用。[19]
1、模糊测度
经典测度是一个非负集函数,使得在空集上取数值0,在全空间上取数值1,测度要满足可加性。[20]日本学者sugeno于1974年推广了经典的概率测度,将经典概率中的可加性条件替换为约束条件较弱的单调性,提出了模糊测度的概念,并定义了模糊测度的积分。[21]现假设X是一个非空集合,F是由非空集合X的某些子集构成。
定义2:[22]当映射g:F→[0,1]满足条件:
(1)有界性,g(Ø)=0,g(X)=1。
(2)单调性,∀A,B∈F,若A⊆B,则g(A)≤g(B)。

则称g为模糊测度,(X,F)即为模糊可测空间,(X,F,g)即为模糊测度空间。
2、模糊积分
在模糊测度的基础上,模糊积分可以看成是一种非线性函数,Sugeno积分、Choquet积分是两种常见的模糊积分方式。[23]Sugeno模糊积分是一种选择性合成算子,其特点是强化主要因素的作用,缺点是完全忽视了次要因素的影响。Choquet积分则综合考虑了各种影响因素,避免了Sugeno积分的缺陷。
定义3:现假设(X,F,g)是一个模糊测度空间,f∶X→[0,1]是基于X的可测函数,且A∈F,那么f在A上关于模糊测度g的Sugeno模糊积分可以定义为:
(1-2)
其中,a为阈值,fa={x|f(x)≥a}(a∈[0,1]),A是模糊积分的定义域。
当A=X时,(A∩Fa)=(X∩Fa)=Fa,模糊积分公式成为:
(1-3)
当A=X,X={x1,…,xn}为有限集合时,模糊积分公式成为:
(1-4)
为了表示方便,现假设在不失去一般性的情况下,f(x1)≥f(x2)≥…≥f(xn),则积分公式成为:
(1-5)
其中,Xi={xi,…,xi},∨代表取最大值,∧代表取最小值。
在运用模糊积分进行相关问题评价时,可以将f视为待评价对象在某个属性上的得分值;g表示每个属性的重要程度,即属性的权重;f与g的模糊积分则是待评价对象的整体评价值。此外,模糊积分也可以采用加/乘运算,即Choquet积分。
(四)基于层次模糊积分的绩效评价方法
在模糊积分中,对于包含n个属性的绩效评价问题,需要确定2n-2个模糊测度。相比于其他方法,模糊积分在决策者计算属性和属性集的重要程度方面有着很强的复杂度。为了降低复杂度,提高模糊测度和积分理论解决实际问题的可行度,Sugeno等人定义了λ模糊测度。λ模糊测度是用参数λ描述可加程度,一种受λ值限制的测度是目前应用最广的模糊测度型态。[24]
基于Choquet积分的多层次企业绩效评价模型,其父层属性评价值是由子属性的Choquet积分计算得到。从第三次到第一层逐层进行计算,最后得到整个绩效的综合评价值,并依据综合评价值对各个企业的绩效进行排序。[25]根据AHP方法的基本原理,可以构建基于最大Shapley熵的逐级Choquet积分模型,主要步骤有以下五个:[26]
1、建立评估对象的层次结构
在逐层分解的思想的基础上可以有效构建系统的评估指标体系。一般来说,层次指标体系的基本层次有目标层、准则层和指标层三个层次。[27]递阶层次结构的最上层为目标层,即该指标体系的最终目的,目标层以下可包含数个元素。在基于逐级Choquet积分的层次结构中,父层属性的评价值由子层属性的Choquet积分计算得到,传统的AHP方法中是统计加权平均得到。
2、构造Shapley值两两比较判断矩阵
参考AHP方法在测量评估指标的相对重要程度,引入了9分位的相对重要性比例标度,设定同层属性Shapley值成对比较的标准,可以得到有关属性Shapley值之间的判断矩阵。
3、根据判断矩阵计算各属性的Shapley值
参考AHP方法中属性权重的计算方法,从各层的判断矩阵中求解属性的Shapley值。求解方法和AHP方法类似,求解判断矩阵的最大特征根,计算最大特征值对应的特征向量,进行一致性检验,采用和积法或方根法求得Shapley值。
4、构建最大Shapley熵优化模型并求解
采用最大Shapley熵作为模型的目标函数从而构建优化模型,并求解属性和属性集之间的相对重要程度。

gλ(X)=1
gλ(A∪B)=gλ(A)+gλ(B)+λgλ(A)gλ(B)
∀A,B∈P(X),A∩B=Ø
gλ(A)∈[0,1],∀A∈P(X)
λ>-1
(1-6)
5、求综合评价结果
可以通过Choquet积分从最底层评价矩阵开始,自下而上逐级求得综合评估结果。
三、典型建筑企业绩效评价证研究
(一)企业选择
选取中国ENR60强上榜企业,对上述企业绩效评价方法做实证研究。ENR60强企业均为我国建筑企业中的典型代表性企业,从规模角度代表了我国实力最强的60家建筑承包企业。对这个群体企业绩效的研究是有代表性的。
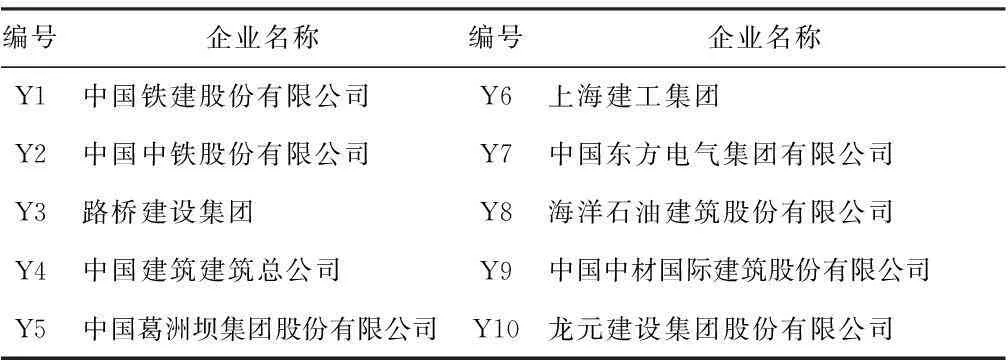
表1 ENR双六十强建筑企业名单
ENR60强中有部分企业是未上市的企业,有部分企业是已上市企业。考虑到本绩效评价方法重点选取了财务数据,并需要对连续数据进行分析,以期发现演化特征。故在ENR60强榜单企业中选取了上市公司进行研究。十家企业名单见表1,这十家企业既有中国规模最大的三家建筑承包龙头企业,如中国中铁、中国铁建、中国建筑(中交建筑因为是在香港上市,数据统计口径有所差异,故没有进入分析样本),也有地方建筑龙头企业,如上海建工,东方电气等。
(二)建筑企业绩效评价指标体系的建立
本文在建立建筑企业综合绩效评价体系时,以企业价值最大化为目标导向,充分考虑企业内外部多方利益相关者,以实现建筑企业整体发展战略为目标。该体系包括了获利能力、经营能力、偿债能力、发展能力四大指标,是一种内部评价指标与外部评价指标相结合,活动过程绩效指标和活动结果指标相结合的综合绩效评价体系,该指标体系能够对建筑企业绩效的经营活动与管理活动进行全方位综合评价。
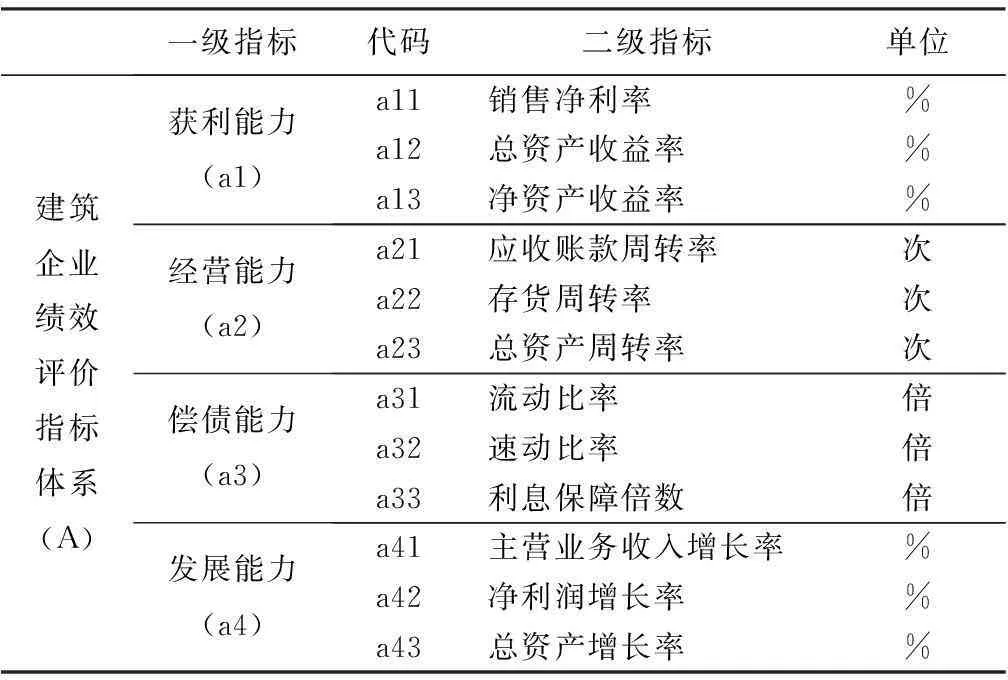
表2 建筑企业绩效评价指标体系
其中获利能力指标主要用于评价企业在生产经营中的获利能力。企业在生产经营活动中的获利一方面可以为企业的扩大再生产提供资本,另一方面也为企业所有者提供利润。获利能力反映了企业的综合素质,是企业赖以生存和发展的基础和进一步发展的保证。良好的获利能力有助于企业获取贷款、增容扩容。评价企业获利能力的指标主要有销售净利率、总资产收益率、净资产收益率。经营能力指标主要是用来反映的建筑企业资金利用效率情况,可以通过企业的生产经营资金周转速度等指标来衡量。经营能力指标值的大小表明企业管理人员运用资本能力高低,是衡量企业运营状况的重要方面。经营能力大小在很大程度上影响了企业获利增长速度和偿债能力,当一个企业经营能力指标值越好,表明该企业的资金利用效果越好。反映企业经营能力的指标主要有应收账款周转率、存货周转率、总资产周转率。偿债能力分析是定量评价企业绩效的重要内容之一。偿债能力的大小可以反映企业按时足额归还债务的能力或保证程度。一般而言,偿债能力指标比率越高,说明企业变现能力越强,资金的流动性、安全性也就越高。衡量偿债能力的指标主要有流动比率、速动比率、利息保障倍数。发展能力指标关系到企业持续生存、债权人长期债权风险程度、出资人未来收益等问题,是企业未来价值的源泉。成长能力较强的企业才能保持盈利的持续性,其长期绩效状况才会好。综合反映企业成长能力的指标主要有主营业务收入增长率、净利润增长率、总资产增长率。
(三)模型构建与数据整理
根据表2建立了基于Choquet积分的多层次建筑企业绩效评价模型,其结构示意图如图1所示。
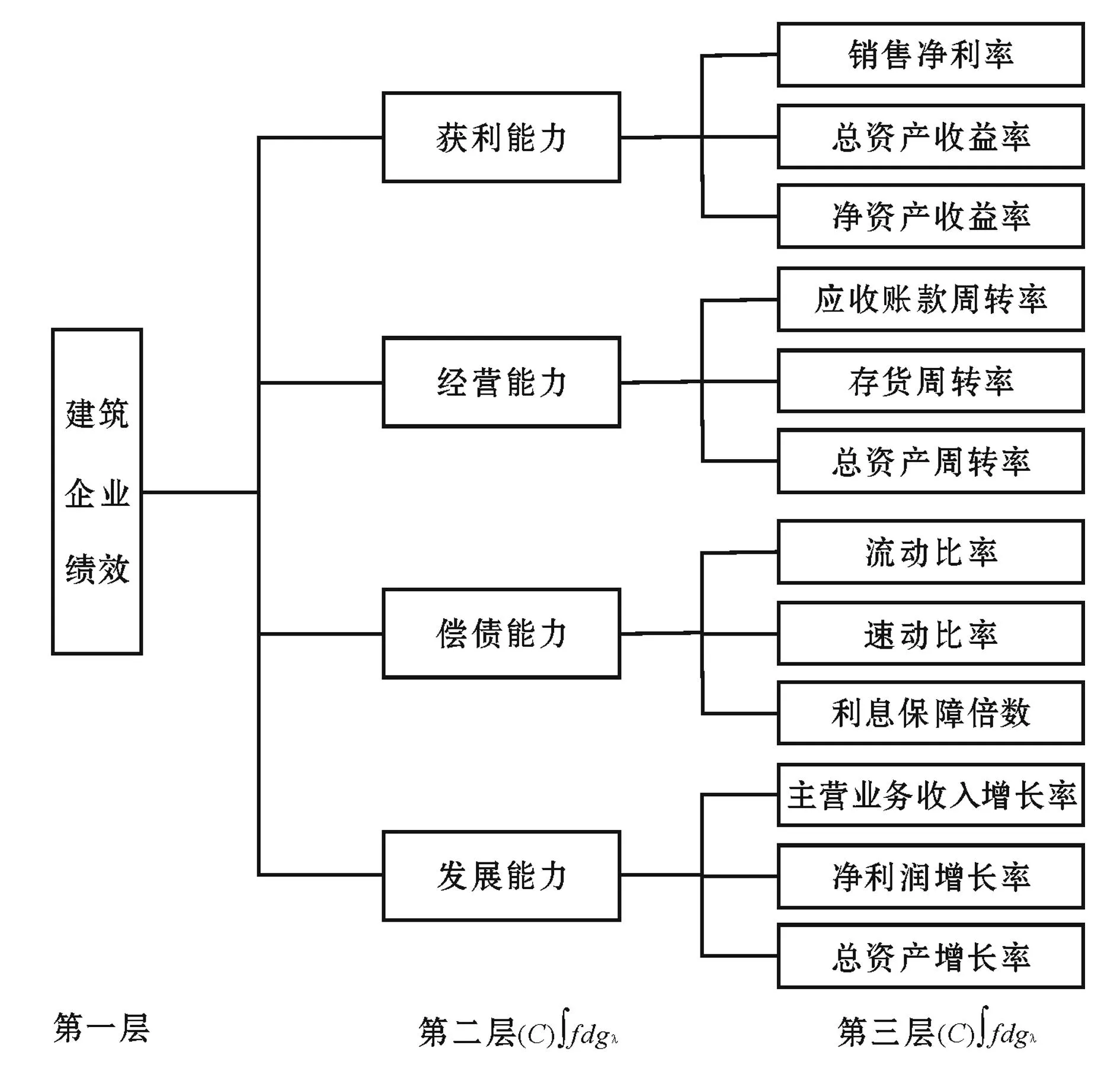
图1 基于Choquet积分的多层次建筑企业 绩效评价模型
建筑企业绩效评价模型构建需要两部分数据:各个指标Shapley值的比较判断矩阵,以及建筑企业在各个指标上的得分。本章借鉴AHP方法,请工程领域资深专业人士进行多轮调查,得到相关指标的判断矩阵;而建筑企业的指标数据则从各建筑企业的近年年报中获取。
首先请专家按照对同一层次的多个指标两两比较,将比较结果按照1-9标度法表示,可得两两判断矩阵。判断矩阵中的值aij表示评估指标i相对于评估指标j的重要程度,并满足如下条件:aij>0,aij=1/aij,aij=1。SA,Sa1,Sa2,SAa3,Sa4是建筑企业绩效评价指标体系中本层与它有关联的各要素(即子属性)之间的相对重要程度Shapley值的判断矩阵。



经检验,SA,Sa1,Sa2,Sa3,Sa4中的判断矩阵均满足AHP方法中的一致性要求,所以可以利用方根法处理上述矩阵,从而得到各层属性的Shapley值,具体结果如下:
根据最大Shapley熵约束规划模型,本文采用Matlab程序里的最优化算法来求解模型,从而得到各属性集的模糊测度,详细结果具体如表3和表4。

表3 建筑企业绩效评价一级指标和指标集的模糊测度
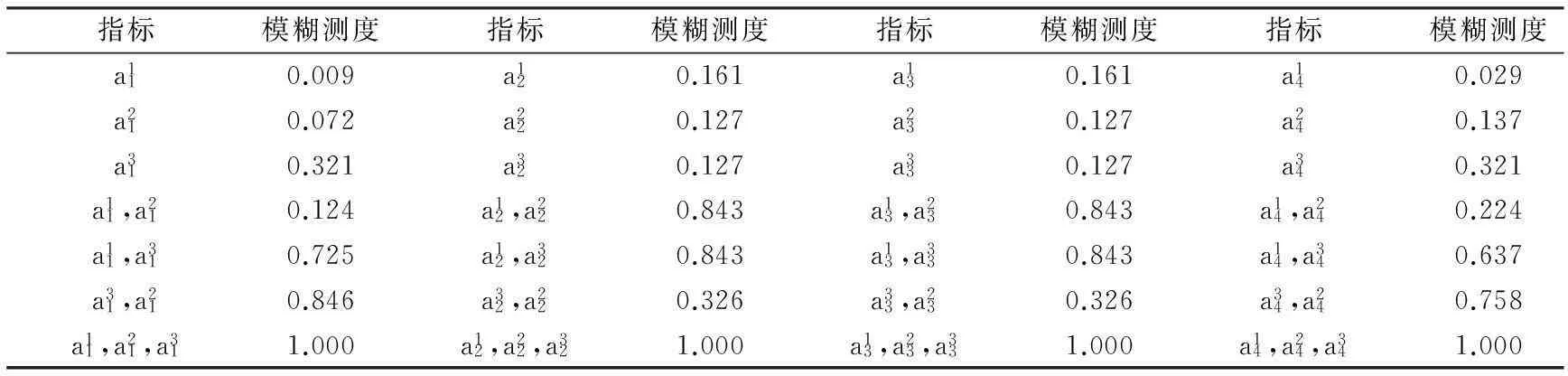
表4 建筑企业绩效评价二级指标和指标集的模糊测度
(四)模糊积分模型结果分析
应用Choquet积分评价方法计算各建筑企业绩效的模糊积分值(见表5)。从评价结果看出,综合评价值虽不能反映具体的经济效益情况,但能对各建筑企业的经济效益进行排序。

表5 近年ENR60强中10家上市建筑企业绩效评价结果
(五)与TOPSIS模型结果比较分析
为了更好地分析考虑指标之间的相关性对建筑企业绩效评价结果带来的影响,本部分将Choquet积分得到的评价结果与常用的TOPSIS方法和加权平均方法得到的结果进行比较,从评价结果的不一致性来分析考虑指标相关性对评价的影响。文中的Choquet积分评价结果与TOPSIS模型等方法结果比较,具体比较结果见表6。
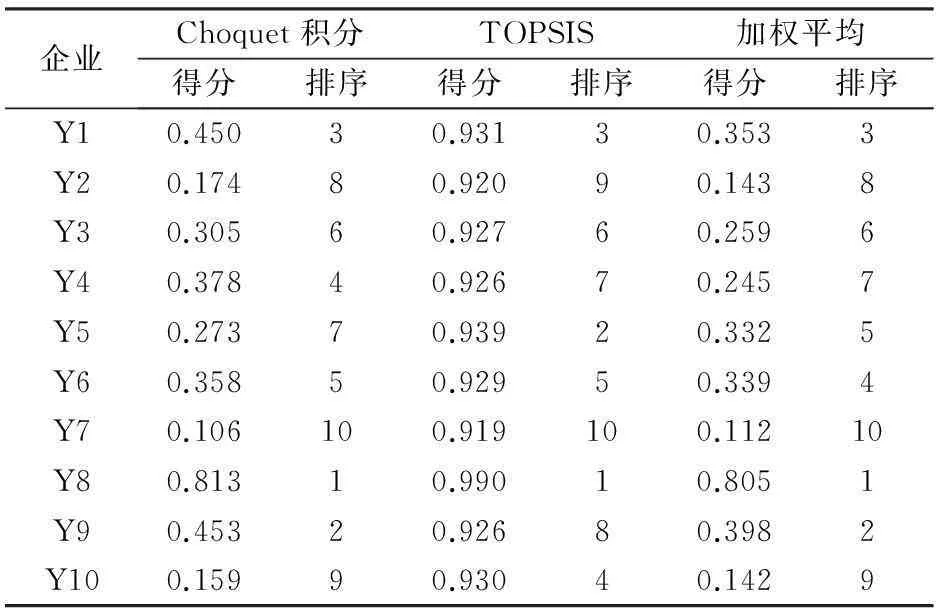
表6 Choquet积分评价结果与其他方法结果的比较
由表6可以看出,Choquet积分法和TOPSIS方法下的十家企业的评价排序是有一些不同的:首先,从得分差距看,Choquet积分法下的排名各企业得分差距拉的很开,从数值上,第一名是0.813,最后一名是0.106,差距约为7.6倍,其他各名次之间也都有明显的差距。而TOPSIS方法下的排名则差异不大,十家企业的排名差异均在小数点后百分位上,从数值上,第一名是0.990,最后一名是0.919,差距非常小,说明TOPSIS方法下的排名区分度不高。其次,从具体企业排名看,Y5、Y9和Y10三家企业排名位次差异较大,Y5为中国葛洲坝集团公司,在Choquet积分法下排名为第七名,属于排名靠后的企业,而在TOPSIS方法下,则排第二名,仅次于排名第一的海洋石油建筑公司。而我们从葛洲坝和其他如中材国际等企业近年的综合表现看,显然中材国际要优于葛洲坝集团,而在TOPSIS方法下却把中材国际这家企业排了倒数第二位。
根据前文的定义可知,独立性多属性合成法(加权平均法)是Choquet积分法的一个特例。从表6的结果可以看出,独立假设条件下得到的综合评估值不同程度上要高于用Choquet积分法得到的的综合估值,分析原因,可能是由于指标设置时同层属性间存在者一定的冗余关系,加权平均法无法考虑这种关联关系,从而导致评价值被高估。因此,对Choquet积分法下的排序和加权平均下的排序也进行了对比,发现在两种方法下,排序情况差异不大。首先,从各企业得分差距看,基本上没有大的差异,说明两种方法在区分度方面有着一致性。其次,主要排名企业的差异不大,仅有Y4中国建筑在Choquet积分法排到了第四位,而在加权平均下排到了第七位,这主要是因为中国建筑是中国目前流通市值最大的企业,在具体指标方面的一些差异都会造成排名的不同。综合比较,说明Choquet积分法方法的有效性。
四、总结
企业绩效评价是一个涉及诸多因素的复杂评价过程,伴随着企业业务的多元化及外部环境的多变性,人们对复杂管理系统中不确定性的关注在未来将不再仅仅局限于业务特点的要素本身,更多地会关注于要素或者系统结构相互之间关系的不确定性。本文针对传统绩效评价模型无法有效地刻画出评价指标相关性的问题,引入最大Shapley熵原理计算属性和属性集的重要程,然后运用Choquet积分方法来评价企业绩效,是一种比较理想的企业绩效的评价方法。在实证中也进一步验证了Choquet积分法方法的有效性。
参考文献:
[1] 雷箐青.转轨时期国有企业绩效评价方法研究[J].财会通讯,2012,(5):75-76.
[2] 臧晶.企业绩效评价的理论基础[J].工业技术经济,2010,29(10):37-40.
[3] 刘贵清.基于DEA与AHP方法的中小企业绩效评价模型[J].统计与决策,2013,(14):173-175.
[4] 马建峰,何枫.包含共享投入与自由中间产出的技术创新两阶段DEA效率评价[J].系统工程,2014,32(1):1-9.
[5] Charnes, Cooper, Rhodes. Measuring the efficiency of decision making units[J].European Journal of Operational Research,1978,2(6):429-444.
[6] 高丹丹.我国装备制造业技术创新综合效率评价研究—基于CCR模型和BCC模型[J].价值工程,2013,(6):1-3.
[7] CooperW W, Seiford LM, T oneK. Data EnvelopmentAnalysis: AComprehensive Text with Models, ApplicationsReferencesandDEA- Solver Software[M]. Kluwer AcademicPublishers, Boston,2000.
[8] RS Kaplan,DPNorton.Using the balanced scorecard as a strategic management system[J].Harvard business review, 1996.
[9] 路媛媛.企业经营绩效评价研究综述及展望[J].财会通讯,2012,(5):57-58.
[10] Menches, C. L., A. S. Hanna. Quantitative measurement of successful performance from the project manager's perspective[J].Journal of Construction Engineering and Management, 2006, 132(12): 1284-1293.
[11] Ilhan Yu, Kyungrai Kim, YoungsooJung ,Sangyoon. Comparable performance measurement system for construction companies[J]. Journal of Management in Engineering, 2007, 23(3): 131-139.
[12] 张文泉,张世英,江立勤.基于熵的决策评价模型及应用[J].系统工程学报,1995,10(3):69-74.
[13] 邓聚龙.灰色系统论文集[C].武汉:华中理工大学出版社,1989.
[14] 李芊,李倩林.基于熵权—TOPSIS方法的房地产投资决策评价模型实证研究[J].企业经济,2011,(3):120-122.
[15] Malakooti B, Zhou Y Q. Feedforward artificial neuralnetworks for solving discrete multiple criteria decisionmaking problems [J]. Management Science,1994,40(11):1542-1561.
[16] 李秀珠,余忠.我国建筑业上市公司财务绩效评价的实证分析[J].技术经济,2009,28(10):116-118.
[17] Yager R R. On the entropy of fuzzy measures[J]. IEEE Transactions on Fuzzy Systems, 2000, 8(4): 453-461.
[18] Ishiia K, SugenoaM. A model of human evaluation process using fuzzy measures[J]. International Journal of Man-Machine Studies, 1985, 22(1): 19-38.
[19] 管涛,冯博琴.Choquet模糊积分的粗糙性及信息融合[J].西安交通大学学报,2004,38(12):1251-1255.
[20] Zhenyuan W, J.Klir G. Fuzzy measure theory[M]. New York: Plenum Press, 1992.
[21] Sugeno M. Fuzzy measures and fuzzy integrals: a survey[J]. Fuzzy automata and decision processes, 1977, 89: 102.
[22] Murofushi T, Sugeno M. A theory of fuzzy measure representations, the Choquet integral and null sets[J]. J. M ath. Anal. Appl., 1991,159: 532-549.
[23] Chiang J H. Aggregating membership values by a Choquet-fuzzy-integral based operator[J]. Fuzzy Sets and Systems, 2000, 114(3): 367-375.
[24] Grabisch M. Fuzzy integral in multi-criteria decision making[J]. Fuzzy Sets and Systems, 1995, 69(3): 279-298.
[25] Chen Y, Tzeng G. Using fuzzy integral for evaluating subjectively perceived travel costs in a traffic assignment model[J]. European Journal of Operational Research, 2001, 130(3): 653-664.
[26] 章玲,周德群.基于Choquet积分的层次多属性决策方法研究[J].南京航空航天大学学报,2007,39(6):824-828.
[27] 吕镇邦,周波.基于Shapley熵和Choquet积分的层次化风险评估[J].北京邮电大学学报,2009,32(6):83-87.
A Study on the Model of Performance Evaluation Based on
Choquet Integral: A Case Study of Construction Enterprise
Wang Wenzhou1Shi Limeng1Lin zefu2
(1. School of Business, Beijing Normal University, Beijing 100875, China;
2. School of Management Science and Engineering, Central University of Finance and Economics, Beijing 100081, China)
Key words: performance evaluation; correlation of index; Shapley entropy; Choquet integral
责任编辑:王明舜

